波片延迟量在0°∼360°的高精度测量方法研究
2023-07-03万凡钟悦屈中权徐稚张辉彭洋
万凡,钟悦,屈中权,徐稚,张辉,彭洋
(1 中国科学院云南天文台,昆明 650216)(2 中国科学院大学,北京 100049)
0 引言
波片是偏振光学技术中十分重要的偏振光学元器件,它可以改变入射偏振光的偏振状态,被广泛的应用于光弹力学、现代光通讯技术、医疗诊断和光学精密测量中[1]。在太阳物理研究领域中,太阳各种剧烈大气活动现象如日珥爆发、耀斑和日冕物质抛射(Coronal Mass Ejection, CME)与太阳磁场密切相关[2],而国际上主流的太阳磁场观测手段是基于Zeeman 效应对太阳磁敏线的偏振态及其强度进行观测[3]。太阳望远镜在对太阳大气活动进行高精度偏振观测时,核心设备是偏振分析器与偏振定标单元。偏振分析器对太阳磁敏线的偏振信号进行调制,偏振定标单元对太阳望远镜自身的偏振误差进行定标,二者均使用了波片这种偏振相位延迟器[4]。随着太阳物理研究领域的日益深入,太阳物理学家对太阳磁场的偏振测量精度要求达到10−4量级乃至更高,如美国于2019年建成的全球最大太阳光学望远镜(Daniel K, Inouye Solar Telescope, DKIST)其偏振测量精度为5×10−4Ic[5],德国2012年建成的太阳望远镜(GREGOR Solar Telescope, GREGOR)其偏振测量精度为10−4Ic[6],国内云南天文台即将投入观测的光纤阵列太阳光学望远镜(Fiber Array Solar Optical Telescope, FASOT)其偏振测量精度要求达到8×10−4Ic[7]。为了实现如此高的偏振测量精度,在太阳光学望远镜各子系统的偏振误差分配中,尽量降低由偏振分析器与偏振定标单元带来的偏振误差。由于波片制造工艺等因素的限制,波片真实的相位延迟量δ与理想值之间存在少许偏差。因此,为了实现太阳磁场的高精度偏振测量,波片作为偏振分析器的核心元件,对其相位延迟量δ和方位角的高精度测量方法的研究是十分必要的[9]。
目前,对于波片相位延迟量与快轴方位角的测量方法可分为光强调制法[9-13]、光谱扫描法[13]、补偿法[15]、干涉法[16]和椭偏仪法[17-18],不同测量方法具有各自不同的优缺点及适用范围[9-10]。其中,光谱扫描法测量延迟量为180°的波片,其测量精度高,但对于延迟量为非180°的波片,其延迟量与初始方位角测量误差大;补偿法无法准确测量波片的快轴方位角,其延迟量测量精度完全依赖于标准补偿器件自身在不同波长处的相位延迟量精度;干涉法同样存在着无法准确测量波片快轴方位角的缺陷,其延迟量的测量精度同样依赖于干涉仪自身的分辨本领与白光干涉条纹的重复定位精度;至于椭偏仪法,其测量精度高且是无接触测量,能够实时高精度的测量出待测样品的偏振态与材料特性,如相位延迟量、快轴方位角、材料厚度和折射率等,是测量精度最高的偏振测量方法之一。但椭偏仪在正式测量之前需要对自身进行高精度的偏振定标,且椭偏仪的待测可用空间有限,无法用来测量较大的待测样品和仪器偏振特性;至于光强法,其测量装置简单、操作方便、测量结果实时快速且可利用的待测空间较大,可测量的待测样品种类,大小均不受限制。但光强法易受到探测器光电响应的非线性效应影响,除此之外光强法无法准确测量延迟量为180°的波片。针对上述光强测量法的缺陷,本文在详细分析了光强法的误差来源后,对各项误差进行了抑制并对探测器的非线性效应进行矫正。此外,在拟合光强法的测量基础上结合光谱分析法,实现了对非消色差波片延迟量为0°~360°的精确测量。整套测量系统的光路除终端光强接收设备需更换外,其它不变,该系统可实现任意延迟量与快轴方位角的精确测量,为后续进一步测量偏振分析器的偏振特性提供了测量基础。
1 测量原理与测量系统
1.1 测量原理
波片延迟量与快轴方位角的测量系统光路原理如图1 所示,拟合光强法中,出射白光经准直系统准直成平行光后依次通过孔径光阑、窄带滤光片、起偏器、待测非消色差波片、检偏器,最后被光功率计探测,整个测量过程中,待测波片被高精度步进电机带动匀速旋转。光谱分析法中,上述测量光路不变,仅需移除窄带滤光片,并将光谱仪移入终端替换光功率计作为光强接收设备,此时不旋转待测波片。以起偏器的透过轴作为主轴方向即x轴正方向,光传播的方向为z轴正方向,依此建立右手全局坐标系。

图1 波片测量光路原理图Fig.1 Optical schematic diagram of measurement for waveplates
在利用拟合光强法测量待测波片的延迟量与快轴方位角的过程中,根据各偏振元器件的Muller 矩阵,光功率计接收到的调制光强Iout可表示为
式中,Iin为入射光强;τ为整个测量系统的透过率;[1,0,0,0]T为光强的Stokes 输入矢量;MPG(θ1)为起偏器的Muller 矩阵,θ1=0°;MWP(θ2(initial)+n⋅Δθ,δ)为待测旋转波片的Muller 矩阵,其中初始快轴方位角θ2(initial)未知,Δθ2为旋转步长,n为旋转步数,δ为延迟量未知;MPA(θ3)为检偏器的Muller 矩阵,其偏振透过轴的方位角为θ3;[1,0,0,0]为光强的Stokes 响应矢量;Iout为光功率计探测到的调制光强。
将线偏振元器件与波片的Muller 矩阵[19]代入式(1)并展开,探测到的调制光强Iout与待测波片延迟量δ可表示为矩阵形式有
由式(2)、(3)可知,调制光强Iout与cosδ构成了一个线性系统,为了充分降低线性系统的随机误差,如入射光强Iin的抖动、系统透过率τ、旋转电机的定位精度等因素对测量结果的干扰,提高系统的测量精度与稳定性,需要确定合适的检偏方位角θ3与波片的旋转步长Δθ2。系统矩阵D的谱条件数cond(D)2[20-21]越小,测量系统的测量精度越高,其稳定性越好。由于系统矩阵D中波片初始快轴方位角θ2(initial)为待测量,本文模拟仿真了θ2(initial)分别为−80°、−60°、−40°、−20°、0°、20°、40°、60°、80°九种情况下的cond(D)2随检偏方位角θ3、波片旋转步长Δθ2的综合变化结果。如图2 所示。

图2 系统矩阵D 的谱条件数(cond(D) 2)Fig.2 Condition number (cond(D) 2)of system matrix D
由图2 可知,当检偏方位角θ3在±45°以内且待测波片旋转步长Δθ2在10°以内时,图2 所示的9 种系统矩阵D的谱条件数cond(D)2较小,系统稳定性较好,测量精度较高。当检偏器方位角θ3为±90°或旋转步长Δθ2为45°的整数倍时,图2 所有的系统矩阵D的谱条件数cond(D)2均很大,表明此种情况下系统的稳定性很差,系统对随机误差很敏感。再结合整个测量过程中,数据点太少影响测量精度,数据点太多则采集时间过长。综上考虑,本测量系统确定检偏器方位角θ3为45°,待测波片的旋转步长Δθ2为3°,旋转步数n为120 步。将θ3=45°、Δθ2=3°带入式(1)可得Iout为
式中,未知参数为τIin、δ、θ2(initial),对光功率计采集到的光强Iout进行非线性最小二乘法拟合,即可拟合得到待测波片延迟量δ与快轴初始方位角θ2(initial)。此外,由Iout对δ求偏导可知,当δ=0°(360°)或δ=180°时,,此时光强Iout处于极大值或极小值,对延迟量δ的变化不敏感。此区域内测量系统的信噪比低,测量误差大。因此对于特定波长下δ=180°的非消色差波片,上述拟合光强法无法精确测量该波片的延迟量δ。
对于拟合光强法无法精确测量延迟量在180°附近的非消色差波片的缺陷,基于该测量系统结合光谱分析法可实现精确测量。此时不旋转待测波片,光谱仪对经起偏器、待测波片、检偏器的白光进行色散,通过分析白光色散光谱即可精确测量波片的延迟量δ与快轴初始方位角θ2(initial)。由式(4)可知,此时色散光谱各波长点处的光强值与待测波片延迟量δ、快轴初始方位角θ2(initial)的关系为
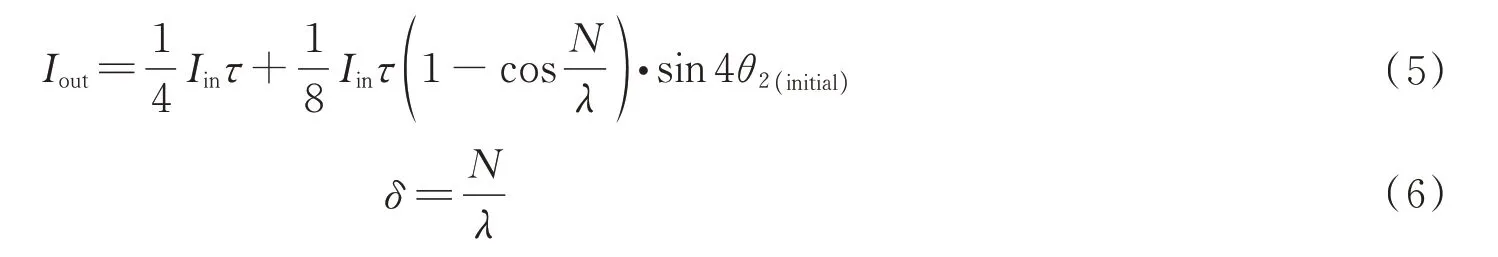
式中,未知参数为τIin、N、θ2(initial),N=2π·(no(λ)−ne(λ))·d,在参考波长为λref的条件下,no(λ)为待测波片o光方向的折射率,ne(λ)为e 光方向的折射率,d为波片的光学厚度。在Δλ≤20 nm 时,no(λ)、ne(λ)随波长λ变化很小可认为是常数,则待求参数N同样为常数,再根据公式(6)即可得到非消色差波片的延迟量δ与延迟量δ=180°的真正参考波长λref(real)。
但对于延迟量δ≠180°的非消色差波片而言,运用光谱分析法测量该波片的延迟量与快轴方位角的精度较差。由拟合式(5)Iout对λ求偏导可知,N=kπλ时,,此时Iout为极大值或极小值。若N≠kπλ,,此时拟合式(10)的斜率与N密切相关。而N是波长λ的函数,波长λ变化范围较大,则前提近似no(λ)、ne(λ)为常数不再成立,N此时是一个变化的参数,且整个系统的透过率也将会发生变化,待拟合参数不在具有唯一性与确切的物理意义。故延迟量δ≠180°的波片,不能使用光谱分析法精确测量其延迟量与快轴方位角。
1.2 测量系统
根据图1 所示的波片延迟量与快轴方位角测量原理图,在实验室建立了对应的波片测量系统如图3 所示。拟合光强法中,白光光源1 发出白光经准直系统2 准直后经孔径光阑3、滤光片4、起偏棱镜5 成为单色线偏振光,线偏振光再经待测波片6、检偏棱镜7 最后被光功率计8 所接受。整个测量过程中,高精度电机带动待测波片匀速旋转。而在光谱分析法测量过程中,需将滤光片4 移出测量光路,且将终端光强接受设备更换为光谱仪与配套的电荷耦合器件(Charge Coupled Device camera, CCD)相机9,此时不旋转待测波片。图3 中,构成波片检测系统所有的光学元器件均被清楚的标明,其关键的系统参数将被详细阐述。
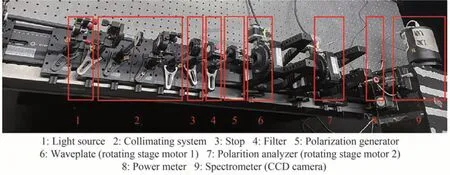
图3 波片测量系统光路实物图Fig.3 Optical photograph of measurement system for waveplate
1)白光光源:其型号为Edmund,MI-150,波长范围为200 nm~1 100 nm,由稳压电源供电,其光强稳定性标称≤2%。
2)准直系统:准直系统由显微物镜、孔径光阑、准直透镜构成,将入射白光准直成平行光束。
3)孔径光阑:调节经准直系统准直后的平行光束的尺寸为5 mm。
4)滤光片:其中心波长为632.8 nm,FWHM 为3±0.6 nm,透过率≥80%,口径为25.4 mm。将待测波片的标定参考波长λref从白光中滤出。
5)起偏器:起偏器为Glan-Taylor 棱镜,其工作波段为350 nm~2 300 nm,消光比大于100 000∶1,光束偏离<3′,通光口径为15 mm。
6)待测波片:待测波片是购置的三种商用真零级非消色差波片,标称参考波长为632.8 nm,其延迟量标称分别为δ=180°,128.16°,90°,通光口径均为25.4 mm。待测波片被安装在高定位精度的步进电机(Princeton Instruments,型号C-885.R1)上,步进电机的定位精度为20″,能显著的降低由于电机定位精度不足带来的随机误差。最大旋转速度可达1 000°/s,极大的缩短数据采集时间。
7)检偏器:检偏器同样由Glan-Taylor 棱镜承担。此外,检偏棱镜也被安装在高定位精度的步进电机。
8)光功率计:其型号为THORLAB,PM100D,探测波长范围为400 nm~1 100 nm,探测量程为0.05 μW~50 mW,能量分辨率为0.01 μW,探测器靶面尺寸为9.5 mm。
9)光谱仪与CCD 相机:光谱仪型号为Princeton Instruments,SP2750i,其工作波段为350 nm~1 100 nm,焦距f=750 nm,F/9.7,光谱分辨率为0.03 nm@633 nm。配套的2K CCD 相机,其像元尺寸为13.5 μm,波段在400 nm~900 nm,量子效率(Quantum Efficiency,QE)≥90%。此外,为了降低交流电压不稳定带来的随机误差扰动,所有接电设备均由稳压电源供电。
1.3 探测器的非线性效应矫正
在利用拟合光强法测量待测波片延迟量与快轴方位角之前,首先需要确定光功率计的非线性效应系数,并在后续的数据处理中,对探测的光强数据进行矫正。光功率计光电响应的非线性效应可表示为[10]
式中,Iout为光功率计显示的光强读数,Ireal是能量计接收到的真实光强,ai(i=0,1,2,…)为非线性响应系数。对于常见的探测器而言,探测器接收到的真实光强其三阶及以上的非线性效应影响不大,可以忽略不计[10-11]。因此只需要对探测到的光强Iout进行二阶及二阶以下的矫正,即可得到真实的输出光强Ireal。
此外,检偏棱镜透过轴相对起偏器透过轴的初始方位角θ3(initial)也需提前测定,此时不装载待测波片,只旋转装载有检偏Glan-Taylor 棱镜的步进电机2(RSM2),以Δθ3=3°为步长,旋转5 圈,光功率计同步采集相应的输出光强Iout。若不考虑光功率计光电响应的非线性效应[10-11],由式(1)可知只旋转检偏棱镜的Iout可表示为
将式(8)进一步展开为
未知参数为τIin、θ3(initial),将光功率计的非线性效应影响考虑进来,结合式(7)和(9)可知光功率计显示的光强读数Iout为
利用最小二乘法对式(10)进行非线性拟合,得到待拟合参数τIin、θ3(initial)、a0、a1、a2。
最小二乘法的拟合公式为[11]
式中,In为波片每旋转一步光功率计采集的光强值,n为旋转步数,Infitting为每步的拟合光强值,χ2为拟合残差。
2 波片测量精度分析
2.1 测量误差来源分析
在整个波片测量系统的设计与建立过程中,已通过稳压电源稳压、搭建准直性优异的光路、采用高精度电机等措施来降低各种随机误差和系统误差。但误差可以降低,却不可能完全消除。根据本测量系统的光学元器件构成,拟合光强法的误差来源主要有光源光强的起伏、准直光束的偏离、窄带滤光片的带宽、步进电机的定位精度和光功率计光电响应的非线性效应。光谱分析法的误差来源有光源光强的起伏、准直光束的偏离、光谱仪的单色精度。其中准直光束的偏离、滤光片的带宽、光功率计光电响应的非线性效应和光谱仪的单色精度是测量系统的系统误差,光源光强的起伏、电机的定位精度是随机误差。
准直光束的偏离引入的系统误差是由于准直光没有完全垂直于光学元件入射,波片延迟量δ随入射角i的变化而变化。以入射角i最大为1°分析[13],中心波长为632.8 nm,计算待测波片的延迟量偏差Δδ/δ为0.006 17%。至于滤光片的带宽Δλ引入的系统误差,本测量系统所采用的窄带滤光片其中心波长在632.8 nm、FWHM 为3±0.6 nm,其Δδ/δ经计算为1.873 0×10−6,可忽略不计。而光功率计光电响应的非线性效应,在本文1.3 节中已经进行了详细阐述并进行了相应的修正。
2.2 波片测量误差的模拟仿真
拟合光强法中光源光强的起伏和电机的定位精度带来的随机误差,是本测量系统需要重点抑制的对象。白光光源由稳压电源供电,但其输出光强任然存在着微小的起伏。在正式测量之前,需要采集光源的光强读数,确认光源的抖动量级及稳定的工作时间。图4 是正式测量之前,利用光功率计采集的光源强度数据。
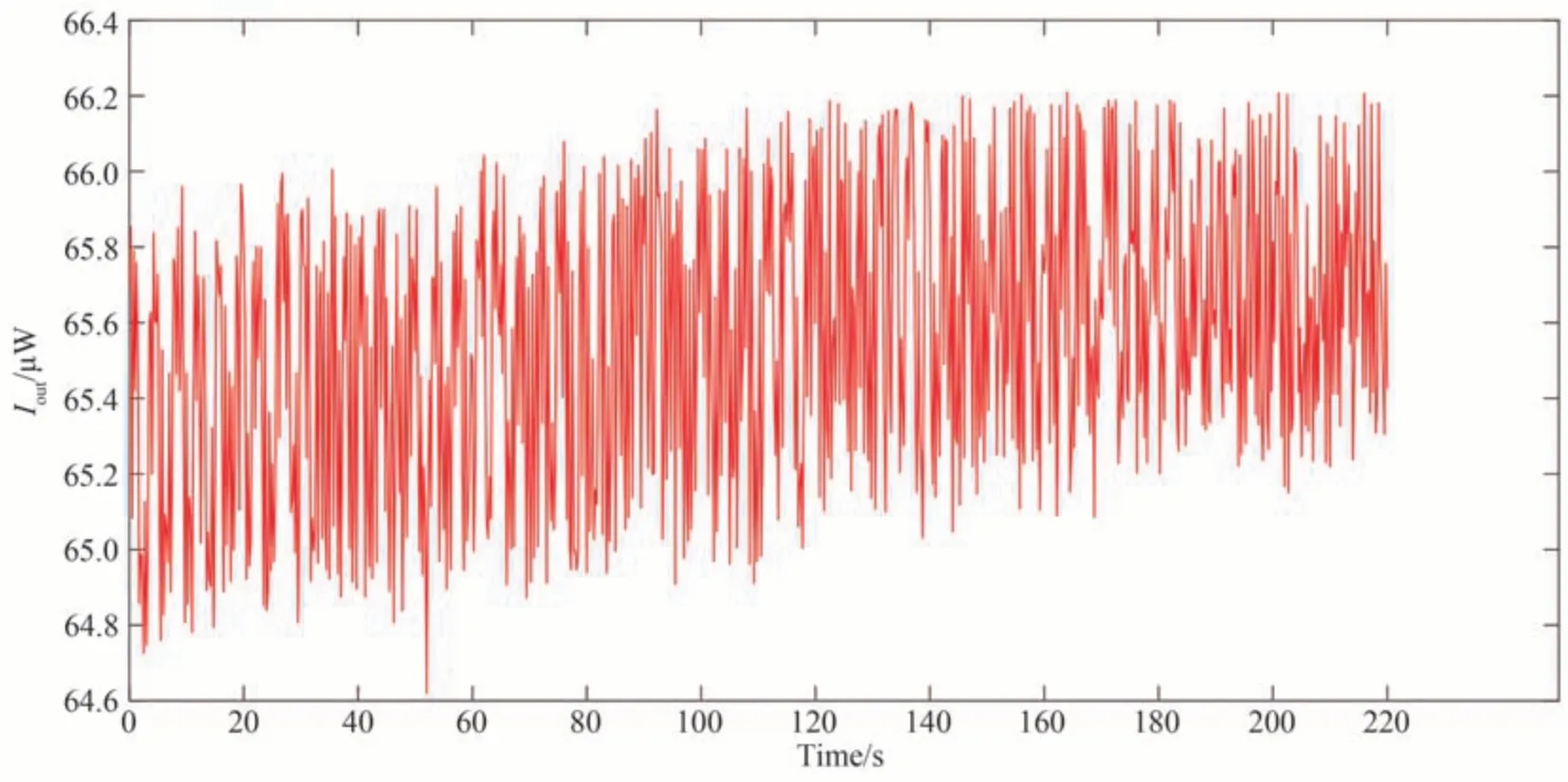
图4 光源辐射强度起伏的实测结果Fig.4 The measured results of the fluctuation of the radiant intensity of the light source
由图4 可知,白光光源的平均光强为65.397 μW,光强起伏的标准差为0.402 μW,最大光强起伏为1.38 μW 是平均光强的2.1%,稳定的工作时间≥4 min。
对于电机的定位精度误差,可进一步细分为波片的初始方位角定位误差,波片的旋转定位误差,检偏器的初始方位角定位误差。对上述随机误差的实际扰动量级进行模拟仿真,分析其对波片延迟量测量的影响。模拟中,光源光强起伏最大为平均光强的2.1%,波片的初始方位角θ2(initial)最大误差为0.5°,波片的旋转定位误差最大为20″,检偏初始方位角θ3(initial)最大误差为0.5°。根据式(1)在Matlab 中对各项误差来源在最大误差限内各产生20 组随机值进行模拟,再根据式(4)进行拟合求解取平均值。模拟仿真结果如图5、图6 所示。

图5 模拟各单项随机误差作用下波片延迟量误差Δδ 随延迟量δ 的变化Fig.5 Simulating the variation of the waveplate′s retardation error (Δδ)with retardation(δ)under the influence of each single random error

图6 各随机误差的综合作用对波片延迟量误差Δδ 的影响Fig.6 The influence of the combined effect of random errors on the waveplate′s retardation error (Δδ)
图5 为各单项随机误差作用下,模拟波片延迟量平均误差Δδ随延迟量δ的变化。由仿真结果可知,光源抖动带来的测量误差是最严重的,最不敏感的是波片旋转角定位误差。图6 为上述所有的随机误差综合作用进行20 次模拟仿真的结果。由图6 可知,当待测波片延迟量δ≠180°时,上述随机误差的综合作用引起的波片延迟量误差Δδ≤0.5°,利用拟合光强法的测量精度较高;当待测波片延迟量δ=180°时,其延迟量误差Δδ≥2.5°,测量误差较大,此时拟合光强法不再适用。
对于特定波长下非消色差波片延迟量δ=180°的测量,根据式(1)、(5)和(6)在Matlab 中对其进行了相关模拟。模拟光源光强抖动最大为2.1%,波长单色带宽最大为0.03 nm,波片初始方位角θ2(initial)最大误差为0.5°,检偏初始方位角θ3(initial)最大误差为0.5°,其结果如图7 所示。
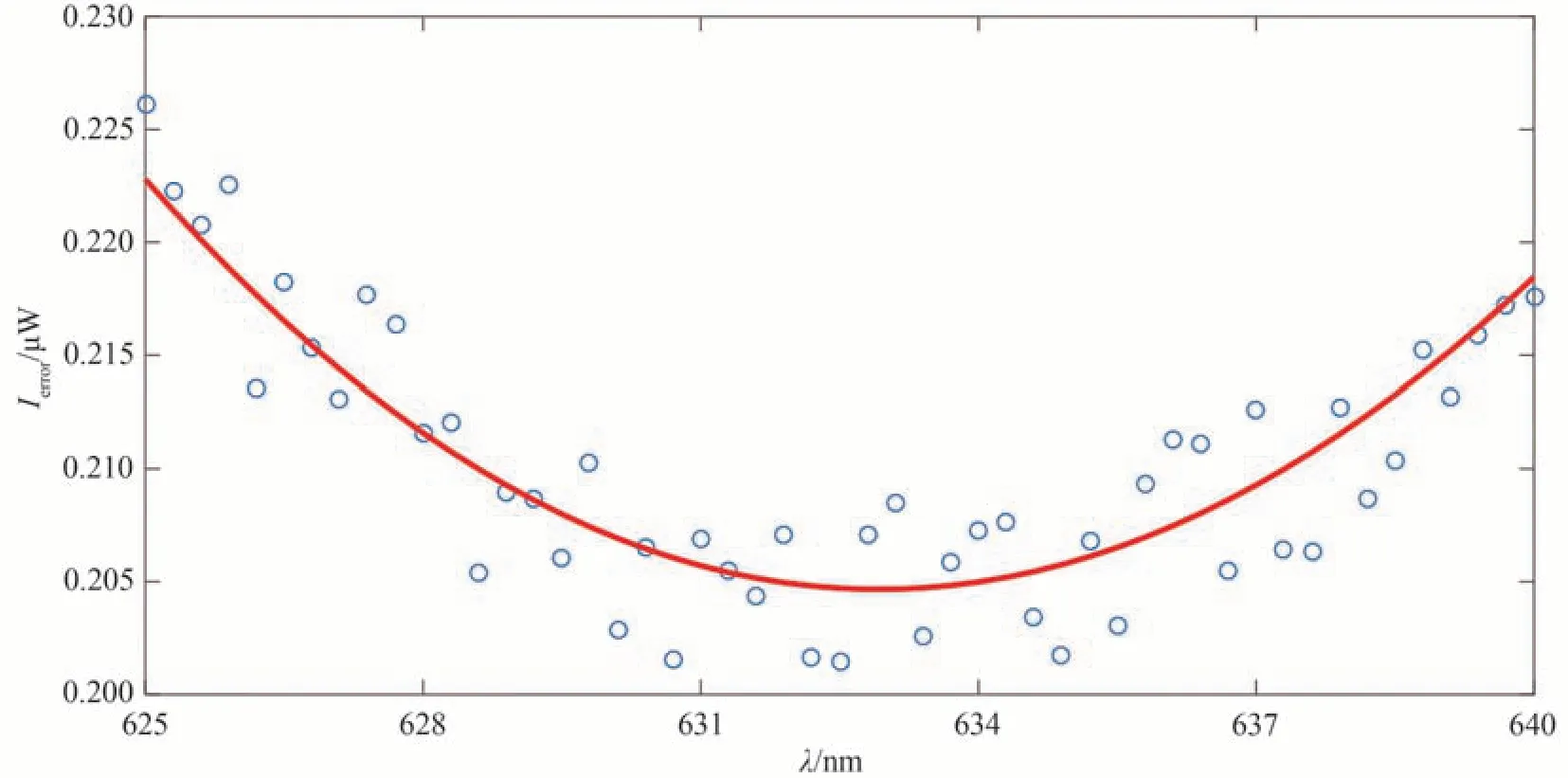
图7 波片待求参数(τIin、N、θ2(initial))的非线性拟合模拟Fig.7 Simulation of nonlinear fitting of Waveplate′s Parameters( τIin,N,θ2(initial))
图7 中蓝色圆圈表示在最大的误差限内利用式(1)模拟得到的输出光强,红色曲线是根据式(5)对带有误差的光强Ierror进行非线性最小二乘法拟合得到的最佳拟合曲线,从而得到待拟合参数N与θ2(initial),再根据式(6)即可得到待测延迟量δ。
模拟的波片其中心波长为632.8 nm,延迟量δ为180°。采用中心波长为632.8 nm、带宽Δλ为15 nm、波长间隔为0.5 nm 进行模拟仿真,得到待拟合参数N为1.992 4 μm,延迟量为δ=180.4°,同时可得到δ=180°对应的中心波长为633.67 nm。由模拟结果可知:此测量方法的测量精度远远高于拟合光强法对于特定波长下非消色差波片δ=180°的测量精度。
3 实测结果分析
3.1 拟合光强法实测结果
在实验室建立了如图3 所示的波片测量系统后,通过旋转检偏棱镜测量探测器的非线性效应系数ai(i=0,1,2)和检偏Glan-Taylor 棱镜的初始方位角θ3(initial)(见式(10))。其测量结果如图8 所示。

图8 探测器非线性效应矫正前后光强对比Fig.8 Comparison of light intensity before and after the nonlinear effect correction of the detector
图8 中深蓝色(×)为光功率计显示的光强Iout,浅蓝色曲线为矫正光功率计非线性效应的真实光强Ireal,粉色曲线为真实光强Ireal与探测光强Iout的残差。拟合得到θ3(initial)=8.065°,a0=−4.76×10−4,a1=0.990 8,a2=−3.27×10−4。
控制电机2(RSM2)将检偏棱镜的初始方位角θ3(initial)旋转到45°,并将待测波片装载在电机1(RSM1)上,电机1 以Δθ2=3°为步长,500° /s 的速度旋转5 圈。利用拟合光强法对中心波长在632.8 nm 附近的1/4λ波片进行了测量,其测量结果如图9 所示。

图9 光强随待测1/4 λ 波片旋转角变化的非线性最小二乘法拟合结果Fig.9 The nonlinear least squares fitting results of light intensity as a function of the rotation angle of the 1/4 λ waveplate
图9 中蓝色圆圈是非线性矫正后的Ireal,红色实线是根据式(11)对Ireal进行最非线性拟合χ2最小的拟合曲线。绿色实线是波片在不同角度下真值Ireal与拟合值Ifitting的残差曲线,最大残差值为1.151 6μW,最大残差比。拟合得到1/4λ波片从0°连续旋转到1800°的延迟量为90.83°,初始方位角为−18.87°。
为了进一步分析1/4λ波片延迟量与初始方位角的拟合精度,本文对矫正后的Ireal进行每360°分离,得到5 组数据,根据式(11)对这5 组数据分别拟合,拟合结果如图10所示。

图10 5 组1/4 λ 波片测量数据的非线性拟合Fig.10 The nonlinear fitting results of measurement data of 5 groups 1/4 λ waveplate
图10(a)中,1/4λ波片延迟量δ(i)的δmax为90.92°,δmin为90.79°,与的RMS 为0.06°。图10(b)中,初始方位角θ2(initial)(i)的最大值为−18.4°,最小值为−19.4°,与的RMS 为0.4°。
利用拟合光强法对参考波长在632.8 nm 附近的0.356λ波片和1/ 2λ波片进行了相同的测量与数据处理。其测量结果如表1 所示。
3.2 其他光强法实测结果对比
为了比较本文所采用的拟合光强法测量非1/2λ波片延迟量δ与快轴初始方位角θ2(initial)的精度,在本测量系统下,本文还对传统的其他两种测量波片延迟量δ的方法进行了相关实测,比较了本测量方法与其他光强法测量波片延迟量δ的精度。
传统光强法采用的一种测量方式是将波片快轴方位角θ2固定在45°,再将检偏器的快轴方位角分别旋转到θ3=0°与θ3=90°的位置,即检偏器透过轴与起偏器透过轴平行与垂直[11-12]。则待测波片延迟量δ为
将1/4λ波片、0.356λ波片进行了上述方法的测量,并将采集的5 组光强数据进行非线性系数矫正,根据式(12)得到待测波片的延迟量δ如图11 所示。

图11 第一种光强法测量1/4 λ 与0.356λ 波片延迟量δ 的结果Fig.11 The results of the first light intensity method to measure the retardation of 1/4 λ and 0.356λ waveplates
由图11 可知,采用这种光强法测量1/ 4λ波片延迟量其均值为92.26°,δmax为93.43°,δmin为90.74°,与的RMS 为0.96°;0.356λ波片均值延迟量为130.28°,δmax为131.70°,δmin为128.85°,与的RMS为0.98°。
另一种光强测量法是将检偏器的快轴方位角θ3固定在45°,旋转待测波片,记录探测光强Iout的最大值Imax与最小值Imin[11-12],则待测波片延迟量δ为
将1/ 4λ波片、0.356λ波片均进行了5 次测量,将采集的5 组数据进行非线性矫正后,根据式(13)得到待测波片延迟量δ如图12 所示。

图12 第二种光强法测量1/4 λ 与0.356λ 波片延迟量δ 的结果Fig.12 The results of the second light intensity method to measure the retardation of 1/4 λ and 0.356λ waveplates
由图12 可知,采用第二种光强法测量1/ 4λ波片的延迟量其均值为91.75°,δmax为92.51°,δmin为90.49°,与的RMS 为0.82°。0.356λ波片的延迟量均值为129.22°,δmax为130.11°,δmin为128.03°,与的RMS 为0.75°。
将传统的两种光强法测量1/4λ波片、0.356λ波片的延迟量δ与本文采用的拟合光强法测量得到的结果进行对比,其结果如表2 所示。三种测量波片延迟量δ的方法分别命名为传统光强测量方法1,传统光强测量方法2,本文的拟合光强法。

表1 1/ 4 λ 波片、0.356λ 波片、1/ 2 λ 波片的非线性拟合结果Table 1 Nonlinear fitting results of1/ 4 λ waveplate,0.356λ waveplate and 1/ 2 λ waveplate

表2 1/4λ 波片、0.356λ 波片延迟量δ 的三种测量方法结果比较Table 2 Comparison of the results of three measurement methods for the retardation of 1/4λ waveplate and 0.356λ waveplate
由表2 可知,传统的两种光强法测量波片延迟量的测量精度较差,相比于本文所述的拟合光强法,其延迟量均值相差1°以上,其RMS 的精度差一个数量级。此外,该两种测量方法均不能测量待测波片的初始方位角θ2(initial)。
对上述三种波片延迟量的测量方法详细分析可知:传统两种光强测量法相对于本系统采用的拟合光强法精度差的原因如下,由谱条件数cond(D)2可知,第一种光强测量法旋转检偏棱镜,其检偏方位角θ3不在±45°以内时,受到系统的偶然误差影响较大;其次,根据光强最大与消光的判断条件,检偏器的透过轴无法精准的旋转到与起偏器的透过轴平行或垂直,第三,该方法采集的数据点较少,易收到偶然误差影响。至于测量方法2 精度不高的原因,第一是步进电机不可能多次正好旋转到光强最大值Imax与最小值Imin的位置处,记录得到的光强极值Imax或Imin存在误差;其次是采集的数据点较少,易收到偶然误差影响。
3.3 光谱分析法实测结果
当波片延迟量δ=180°时,采用拟合光强法测量,系统的信噪比低,测量误差大,表1 的实测结果验证了1.1 的理论分析,此时结合光谱分析法可克服光强法的测量缺陷。设置光谱仪色散的目标谱线λaim为632.8 nm,波长间隔Δλ为0.1 nm,采集波段630 nm~636 nm 的白光光谱,如图13 所示。图13(a)为原始光谱数据,图13(b)为减去背景杂散光和探测器暗电流后的光谱数据。

图13 白光经光谱仪色散在630 nm~636 nm 的光谱数据Fig.13 Spectral data of white light dispersed at 630 nm~636 nm by spectrometer

图14 1/2 λ 波片的灰度值对波长λ 的非线性最小二乘法拟合Fig.14 Nonlinear least squares fitting of the gray value of the 1/2 λ waveplate to wavelength λ

图15 12/λ 波片5 组光谱数据的非线性拟合Fig.15 The nonlinear fitting results of spectral data of 5 groups 1、2 λ waveplate
利用式(11)对净化后的光谱数据进行非线性拟合,待拟合参数为τIin、N、θ2(initial),其单组光谱数据的拟合结果如图14 所示。
图14 中的蓝色十字星表示的是白光经光谱仪色散后在不同波长点的灰度值并进行了归一化处理;红色实线为根据公式(5)对色散光谱拟合得到的最佳拟合曲线,得到待拟合参数N、θ2(initial),再根据公式(6)即可得到待测延迟量δ。将上述测量过程重复5 次,得到波片延迟量δ和初始方位角θ2(initial)如图15 所示。
图15(a)中,1/2λ波片的延迟量δ(i)的最大值为180.30°,最小值为180.26°,拟合均值为180.28°,RMS为0.02°。图15(b)中初始方位角θ2(initial)(i)的最大值为−36.37°,最小值为−36.55°,拟合均值为−36.48°,RMS为0.07°。
4 结论
基于拟合光强法与光谱分析法,设计并建立了一套能够测量非消色差波片延迟量δ在0°~360°范围内任意值与快轴方位角的高精度测量系统。并对该测量系统进行了详细的理论分析、模拟仿真和样品实测。实测结果表明,在进行了系统误差的改正及随机误差的抑制后,基于拟合光强法,通过非线性最小二乘法拟合得到1/4λ波片、0.356λ波片的延迟量δ和初始方位角θ2(initial)测量精度高,波片延迟量的测量比传统两种光强法的测量精度提高一个数量级以上,且能同步测量快轴初始方位角。其测量装置简单易操作,测量结果实时快速。但拟合光强法不适用于延迟量在180°附近的非消色差波片测量,对于延迟量在180°附近的波片在该测量系统下结合光谱分析法进行测量及拟合,测得的延迟量δ和快轴初始方位角θ2(initial)的精度远高于拟合光强法测量的结果。因此,通过本文设计建立的测量系统,可以精确的测量相位延迟量δ在0~360 范围之内的非消色差波片,为精准测量偏振分析器从而实现高精度偏振测量打下基础。
