具有中央凸起的点接触弹流润滑特性研究*

吴海宝 王学锋 胡如夫

（宁波工程学院机械与汽车工程学院 浙江宁波 315336）

光滑配合表面之间的润滑特性已进行了较充分的研究。 但是， 实践中绝对光滑的机械零件表面是不存在的， 在微观上总是凹凸不平的。 因此， 具有微观凹凸特征的配合表面的润滑特性研究是十分必要的。1979 年， WEDEVEN 和CUSANO［1］使用光干涉测量技术测量了具有人工坑槽的弹流点接触配合表面的油膜厚度。 1992 年， KANETA 等［2］使用光干涉法观察了单个凸起对弹流点接触润滑特性的影响。 1994 年，AI 和CHENG［3］进行了移动凹坑下的弹流点接触润滑特性的数值研究。 2000 年， GUANGTENG 等［4-5］实验研究了粗糙表面条件下流体润滑及混合弹流润滑的油膜厚度。 2002 年， 崔金磊［6］对随表面移动的单粗糙峰的非牛顿点接触时变热弹流润滑问题进行了数值研究。 2003 年， FE′LIX-QUIN～ONEZ 等［7］进行了单个隆起通过弹流接触区的实验研究。 2004 年， 杨萍等人［8］对表面带单粗糙峰的线接触时变微弹流润滑问题进行了数值分析。 2007 年， NISHIKAWA 等［9］进行了纵向粗糙度对弹流点接触条件下流体温度影响的数值研究。 2009 年， REN 等［10］提出了适用于粗糙表面线接触混合弹流润滑问题的三维确定性模型。 2012 年，ŠPERKA 等［11］研究了小滑滚比条件下弹流润滑接触的粗糙表面特性。 2015 年， MASJEDI 和KHONSARI［12］研究了表面粗糙度对点接触弹流润滑特性的影响， 并提出了相应的膜厚与载荷公式。 2016 年， ŠPERKA等［13］对粗糙表面弹流润滑特性进行了实验研究， 并观察了使用不同润滑油时的粗糙特征变形。 2018 年，XIAO 等［14］对粗糙表面下线接触弹流润滑的界面法向接触刚度进行了研究。 2019 年， HANSEN 等［15］考察了粗糙表面弹流润滑接触的成膜特性。 2020 年，HULTQVIST 等［16］完成了粗糙表面下热弹流接触的时变分析。 2021 年， QIN 等［17］对单凹坑点接触弹流润滑特性进行了数值研究。

粗糙峰和粗糙谷是微观表面的基本特征， 影响着机械零件配合表面的润滑特性。 本文作者就单个中央凸起的弹流润滑接触进行了数值研究。 其中润滑接触由球-盘接触实现， 球表面中央有一个凸起。 文中建立上述球-盘接触的弹流润滑控制方程， 并进行数值分析， 获得其数值解； 同时对比了凸起表面与光滑表面的压力曲线及油膜曲线， 并考察了载荷及卷吸速度的影响。

1 控制方程

图1 所示为具有中央凸起的弹流润滑点接触示意图。 图中u1和u2分别表示盘和球的速度；w表示施加载荷。 速度u1沿着x轴方向。 坐标系oxyz是右手矢量系统， 其原点o位于盘表面。y轴没有在图中标出。 文中研究针对纯滑动条件， 球静止， 即：u2＝0。

图1 球-盘结构点接触润滑示意Fig.1 Lubrication in point contact with ball-disc structure

用于等温点接触弹流润滑问题研究的稳态Reynolds 方程［17］如下：

式中：ηeff、ρ、h、p和ue分别表示等效黏度、密度、 油膜厚度、 压力及卷吸速度， 且ue＝（u1＋u2）／2。

方程（1） 的边界条件为

式中：xin、xout、 ±yout是计算域边界坐标。

膜厚表达式如下：

式中：h00为计算常数；E′为简化弹性模量；Rx与Ry分别表示x与y方向的曲率半径。

公式（2） 中， 球表面上凸起的形状S1由下式决定：

式中：A、Rd分别表示凸起高度和半径。

球表面上凸起的几何形状如图2 所示。

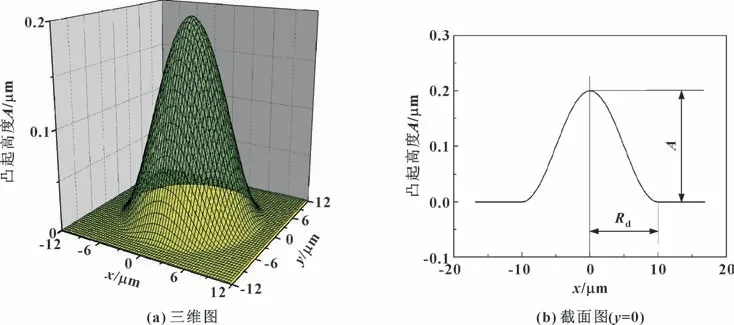
图2 凸起的几何形状Fig.2 Geometry of bump： （a） three-dimensional view； （b） sectional view （y ＝0）

载荷平衡方程表达式如下：

黏压方程表达式如下：

式中：A1＝lnη0＋9.97；A2＝5.1 × 10-9；z0＝α／（A1A2） ；η、η0及α分别表示黏度、 表观黏度及黏压系数。

密压方程表达式如下：

式中：C1＝0.6×10-9；C2＝1.7×10-9；ρ及ρ0分别表示密度和表观密度。

等效黏度表达式如下：

式中：τ为剪应力；τL为极限剪应力，τL＝τL0＋μp，τL0为大气压下的极限剪应力，μ为压-剪应力系数。

求解公式（1） — （7） 构成的方程组， 即可得到其数值解。 其中， 采用多重网格法求解公式（1），使用多重网格积分法求解膜厚方程中的表面变形。 数值程序的公共输入参数为：η0＝1.183 Pa·s，α＝1.71×10-8Pa-1，τL0＝19.8 MPa，μ＝0.036，Rx＝Ry＝0.012 7 m，E′ ＝1.17×1011Pa，A＝0.2 μm，Rd＝10 μm。

2 结果与讨论

图3 显示了存在中央凸起条件下的压力分布和油膜形状。 图中， 压力分布和油膜形状分别只显示了1／2， 关于y＝0 对称的另1／2 没有显示。 由图3 （a）可见， 在存在中央凸起的接触中心附近， 压力出现了剧烈的变化， 首先压力急剧升高， 然后急剧下降， 最后再上升到几乎与光滑润滑表面下的压力值相同。 同时， 无论沿着x或y方向， 中央凸起对压力的影响都集中在接触中心附近。 显然， 接触中心附近的压力升高是中央凸起阻碍润滑油流动导致的。 当润滑油从入口区流动到中央凸起时， 膜厚突然减小， 阻碍润滑油顺利流入接触区下游， 润滑油在中央凸起上游的堆积导致了压力的升高。 当润滑油经过中央凸起以后， 膜厚急剧增大， 压力出现下降。 由图3 （b） 可见， 由于中央凸起上游的压力增大， 油膜出现了一个凹陷，凹陷处膜厚增大。 根据文献［6］， 接触区内的凸起会引起局部高压， 并伴随着局部压力峰； 反过来， 局部高压又使得凸起产生弹性变形， 两配合表面没有直接接触。 所以接触中心附近润滑油膜会变得很薄， 但仍然处于弹流润滑状态。 显然， 图3 所示结果与上述结论是一致的。

图3 压力分布与油膜形状（w ＝77 N， ue ＝25 mm／s）Fig.3 Pressure distribution and film shape （w ＝77 N， ue ＝25 mm／s）： （a） pressure distribution； （b） film shape

图4 所示是有凸起表面与光滑表面的压力及膜厚对比。 由图4 （a） 可见， 在接触中心附近， 压力急剧上升、 然后骤降、 再升高， 最终与光滑表面的压力曲线趋于一致， 其变化与图3 （a） 中一致。 根据公式（4）， 当载荷w一定时， 压力的积分是定值， 即：有凸起表面与光滑表面2 种条件下的压力积分相等。 所以， 接触中心附近压力升高后必然下降， 以满足压力p的积分不变。 由图4 （b） 可见， 中央凸起上游（凸起左侧） 油膜曲线出现了一个明显的凹陷， 其对应于图4 （a） 中的压力升高。 虽然接触表面有弹性变形， 但是中央凸起并没有因此而消失，故接触中心附近膜厚显著变小。 当润滑油离开中央凸起后， 膜厚增大， 逐渐与光滑表面下的油膜曲线趋于一致。

图4 有凸起表面与光滑表面的压力及膜厚对比（w ＝77 N， ue ＝25 mm／s）Fig.4 Film thickness and pressure under smooth and bumped surfaces （w ＝77 N， ue ＝25 mm／s）： （a） pressure distribution （y ＝0）； （b） film thickness （y ＝0）

图5 显示了载荷对压力的影响。 由图5 （a） 可见， 载荷越大， 整体上压力也越大， 这与公式（4）是一致的。 最大压力、 中心压力及中心局部最小压力（接触中心附近的最小压力） 的位置几乎不受载荷影响。 图5 （b） 显示了中心压力、 最大压力、 中心局部最小压力及中心局部压力波动范围随着载荷的变化。 根据图5 （b）， 中心压力和最大压力曲线几乎重合， 表明最大压力几乎在接触中心上。 同时， 中心压力和最大压力几乎都随着载荷的增大而线性增大； 中心局部最小压力随着载荷的增大而几乎线性升高； 中心局部压力波动范围随着载荷增大而几乎线性且缓慢地减小。 并且， 由图5 （a） 还可见， 最大压力和中心局部最小压力间距很小， 即： 最大压力骤然地、 急剧地减小到中心局部最小压力。

图5 载荷对压力的影响（ue ＝126 mm／s）Fig.5 Effect of applied load on pressure （ue ＝126 mm／s）：（a） pressure distribution （y ＝0）； （b） variation of pressure with applied load

图6 显示了载荷对膜厚的影响。 由图6 （a） 可见， 随着载荷的增大， 接触区半径也在增大， 这符合赫兹接触理论， 即： 赫兹接触半径正比于载荷的1／3次方。 同时， 载荷较小时， 中央凸起上游的凹陷更加显著。 由图6 （b） 可见， 中心膜厚与最小膜厚完全相同， 表明中央凸起的最高点没有因为弹性变形而改变位置。 并且， 最小膜厚随着载荷的增大而缓慢地减小， 与图6 （a） 中一致。 显然， 颈缩处膜厚也随着载荷增大而缓慢地减小。

图6 载荷对膜厚的影响（ue ＝126 mm／s）Fig.6 Effect of applied load on film thickness （ue ＝126 mm／s）：（a） film thickness distribution （y ＝0）； （b） variation of film thickness with applied load

图7 显示了卷吸速度对压力的影响。 图7 （a）表明， 卷吸速度越大， 最大压力越小， 而接触中心下游压力有些增大， 保持了整体上压力积分的值不变，参见公式（4）。 同时， 最大压力、 中心压力及中心局部最小压力的位置几乎不受卷吸速度影响。 图7 （b）显示了中心压力、 最大压力、 中心局部最小压力及中心局部压力波动范围随着卷吸速度的变化。 根据图7 （b）， 最大压力和中心压力几乎完全相等， 表明最大压力几乎就在接触中心。 或者说， 最大压力与最小膜厚及中央凸起的最高点在位置上是一致的。 最大压力随着卷吸速度的增大而非线性地减小； 卷吸速度较小时最大压力下降得快， 如：ue＜80 mm／s； 卷吸速度较大时最大压力下降得慢， 如：ue＞80 mm／s。中心局部最小压力随着卷吸速度的增大几乎线性增大。 中心局部压力波动范围随着卷吸速度的增大而非线性地减小， 变化趋势与最大压力相似。 显然， 卷吸速度的增大， 抑制了接触中心附近的压力波动， 使得压力曲线具有向光滑表面下的压力曲线靠近的趋势。已有的研究表明， 卷吸速度的增大使得整体上膜厚增大。 而膜厚的增大会弱化中央凸起对润滑油流动的干扰， 因中央凸起导致的润滑油堆积在整个截面上润滑油数量的占比减小， 从而导致压力波动的减弱。

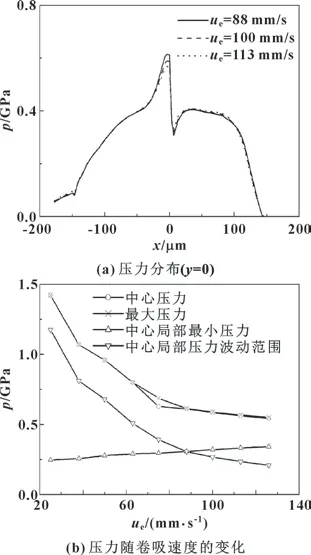
图7 卷吸速度对压力的影响（w ＝19 N）Fig.7 Effect of entrainment velocity on pressure （w ＝19 N）：（a） pressure distribution （y ＝0）； （b） variation of pressure with entrainment velocity

图8 显示了卷吸速度对膜厚的影响。 图8 （a）表明， 膜厚整体上随着卷吸速度的增大而增大。 由图8 （b） 可见， 最小膜厚和中心膜厚几乎完全一致，表明最小膜厚出现在接触中心， 其位置几乎不受卷吸速度影响。 同时， 中心膜厚、 最小膜厚及颈缩处膜厚都随着卷吸速度的增大而几乎线性地增大。

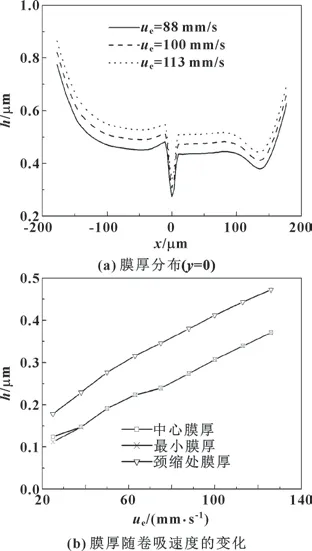
图8 卷吸速度对膜厚的影响（w ＝19 N）Fig.8 Effect of entrainment velocity on film thickness （w＝19 N）：（a） film thickness distribution （y ＝0）； （b） variation of film thickness with entrainment velocity

3 结论

（1） 中央凸起引起了接触中心附近的压力及膜厚的突变。 压力经历了急剧上升、 骤然下降、 再升高并最终与光滑表面的压力曲线重合的过程； 膜厚曲线首先出现了一个凹陷， 然后膜厚骤减到最小值、 再急剧升高并最终与光滑表面曲线重合； 最大压力及最小膜厚几乎都在接触中心。

（2） 随着载荷的增大， 压力分布整体上增大，中心压力、 最大压力及中心局部最小压力几乎线性增大， 中心局部压力波动范围变化不大； 载荷对最小膜厚、 中心膜厚及颈缩处膜厚影响不大。

（3） 随着卷吸速度的增大， 最大压力、 中心压力及中心局部压力波动范围减小， 而中心局部最小压力略有升高； 整个油膜曲线、 中心膜厚、 最小膜厚及颈缩处膜厚都随着卷吸速度的增大而增大。