融合遗忘和知识点重要度的认知诊断模型

刘宇鹏 张雷

融合遗忘和知识点重要度的认知诊断模型

刘宇鹏 张雷

（哈尔滨理工大学 计算机科学与技术学院，黑龙江 哈尔滨 150001）

智慧教育是人工智能的重点研究方向，如何利用试题中知识点并对学生的认知过程进行刻画是重中之重。针对认知诊断模型对学生和试题及其交互信息挖掘不充分的问题，文中提出了融合遗忘和知识点重要度的认知诊断模型。该模型根据学生对试题和知识点的历史交互，结合知识点难度信息引入遗忘因素，缓解了对学生信息挖掘不充分的问题；通过注意力机制获取试题对知识点的考查重要度信息，缓解了对试题信息挖掘不充分的问题；通过Transformer学习学生与试题间的交互，缓解了学生与试题交互不充分的问题。在经典数据集上的实验结果表明，文中模型在Math1、Math2、Assistment数据集上的准确率cc、均方根误差RMSE、受试曲线面积AUC值分别为0.716、0.445、0.776、0.725、0.432、0.807、0.741、0.427和0.779，优于现有的其他对比模型，说明了知识重要度和时效性对于认知建模的重要性。

认知诊断；注意力机制；转换器；知识点重要度；遗忘信息

现在有大量的工作是根据学生的个性化知识进行个性化教育资源推荐，而认知诊断（CDM）［1］在提取学生认知水平时发挥着不可替代的作用。如何通过学生历史学习信息准确刻画其知识掌握水平，是认知诊断研究的关键问题。近年来众多学者提出了许多认知诊断模型，如确定性输入噪音与门模型（DINA）［2］、项目反应理论模型（IRT）［3］、多维IRT（MIRT）［4］和深度IRT模型（DIRT）［5］等。大部分模型直接利用学生对试题的作答记录进行认知诊断，忽略了学生学习过程中的一些重要因素。教育心理学家认为，学习过程不是静态的，学生在学习过程中都会有遗忘过程，因此遗忘因素是学生学习过程中的一个重要因素。另外，认知诊断模型大都将工作聚焦于学生角度，建模学生对知识点的掌握程度，而忽略了试题与知识点间的紧密联系。大多数认知诊断模型在提取学生与试题的交互信息时过于简单，难以捕捉到学生和试题间更深层的复杂关系。针对上述问题，文中提出了融合遗忘和知识点重要度的认知诊断模型。针对认知诊断模型忽略了学生学习过程中一些重要因素的问题，在认知诊断模型基础之上，引入了遗忘信息，文中从知识点的角度出发，将学生对知识点的作答频率和知识点的难度经过神经网络获取遗忘信息，预测过程中新增了一个时间因子拟合时间对遗忘的影响；针对认知诊断模型聚焦于学生角度，忽略了试题与知识点的紧密联系问题，文中从试题角度出发，利用试题和知识点之间的紧密关系，经过注意力机制获取与试题联系更紧密的知识点重要度，更新认知诊断的试题因素；针对认知诊断模型获取学生与试题交互不充分的问题，文中将各个诊断因素进行融合以提升诊断精度。

1　相关工作

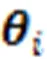
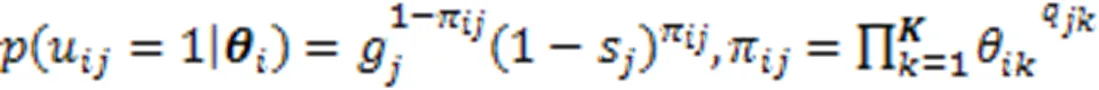
式中：为学生i对试题j的作答结果，；分别为猜测因素和失误因素；为学生对试题知识点掌握程度的总结；为学生i的知识点掌握程度向量；为试题j知识点k的考查情况；K为知识点个数。当学生掌握了试题的所有考查知识点时，取1，否则取0。

DINA具有很好的解释性和可拓展性，是认知诊断中最广泛使用的方法，非常适用对二值计分项目的得分预测。

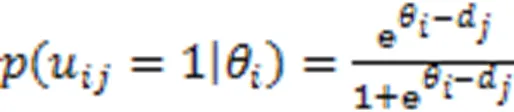
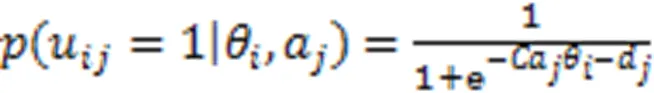
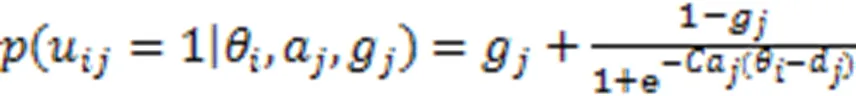
此后许多学者在此基础上进行了改进。Zhu等［6］提出了一种多任务-多维认知诊断框架（MT-MCD），用于同时对不同考试的学生进行评估。Liu等［7］基于模糊集合理论和教育假设，提出了一个模糊认知诊断框架，用来模拟学生的认知水平。Xu等［8］提出了两个新的概率图模型，可提高同伴评估的准确性。这些模型都取得了一定的效果，但大都依赖于人工设计的函数获取交互，不能很好地捕捉学生与试题之间的复杂关系。

深度知识追踪模型第一次将循环神经网络（RNN）用于知识追踪［9］，但其知识追踪只能对学生的试题得分进行预测，不能诊断出学生对知识点的掌握水平，因此不能很好地应用于认知诊断。在深度学习基础上，Gierl等［10］将神经网络应用于小样本认知诊断任务中，取得了不错的效果。Cheng等［5］提出了深度项目反应理论（DIRT）框架，用深度学习代表问题文本中的语义。Wang等［11］针对认知诊断中只使用简单函数获取学生与试题交互导致的诊断精确不够的问题，提出了神经认知诊断，使用神经网络获取学生与试题的交互函数。然而，影响诊断结果的因素有很多，研究表明，知识点重要性对诊断结果的影响很大。在知识追踪任务中，李晓光等［12］将知识点重要性与试题结合，提升了得分预测准确度，证明了知识点重要度与试题结合的必要性。另外，现有的认知诊断工作大都处在静态场景中，即认为学生的认知状态在某个阶段不发生变化。这不符合实际，因为现实生活中，每个人都有一个遗忘过程［13］。因此，遗忘因素是非常重要的诊断因素。

2　方法描述

文中提出的融合遗忘和知识点重要度的认知诊断模型FK-CD包括输入部分、知识点重要度获取模块、学生遗忘信息获取模块、信息融合与得分预测部分，如图2所示。

2.1　知识点重要度获取模块

在真实世界中，每个试题考查的知识点重要度是不同的。有的知识点作为试题的重点考查，是解答该试题的关键；有的知识点则考查程度不高，对学生的掌握程度要求也不高。因此，不同知识点相对于该试题的重要度对学生答题能力有影响。文中使用注意力机制来获取试题对知识点的考查侧重（关联），计算方法为

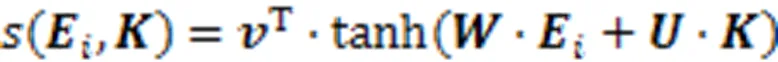
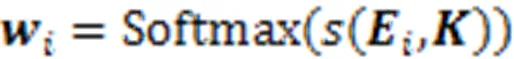
在得到知识点考查权重后，带有知识点考查重要度的试题表示向量为

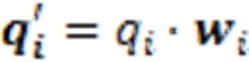
2.2　遗忘信息获取模块

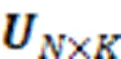
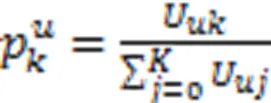
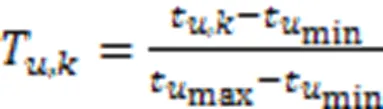
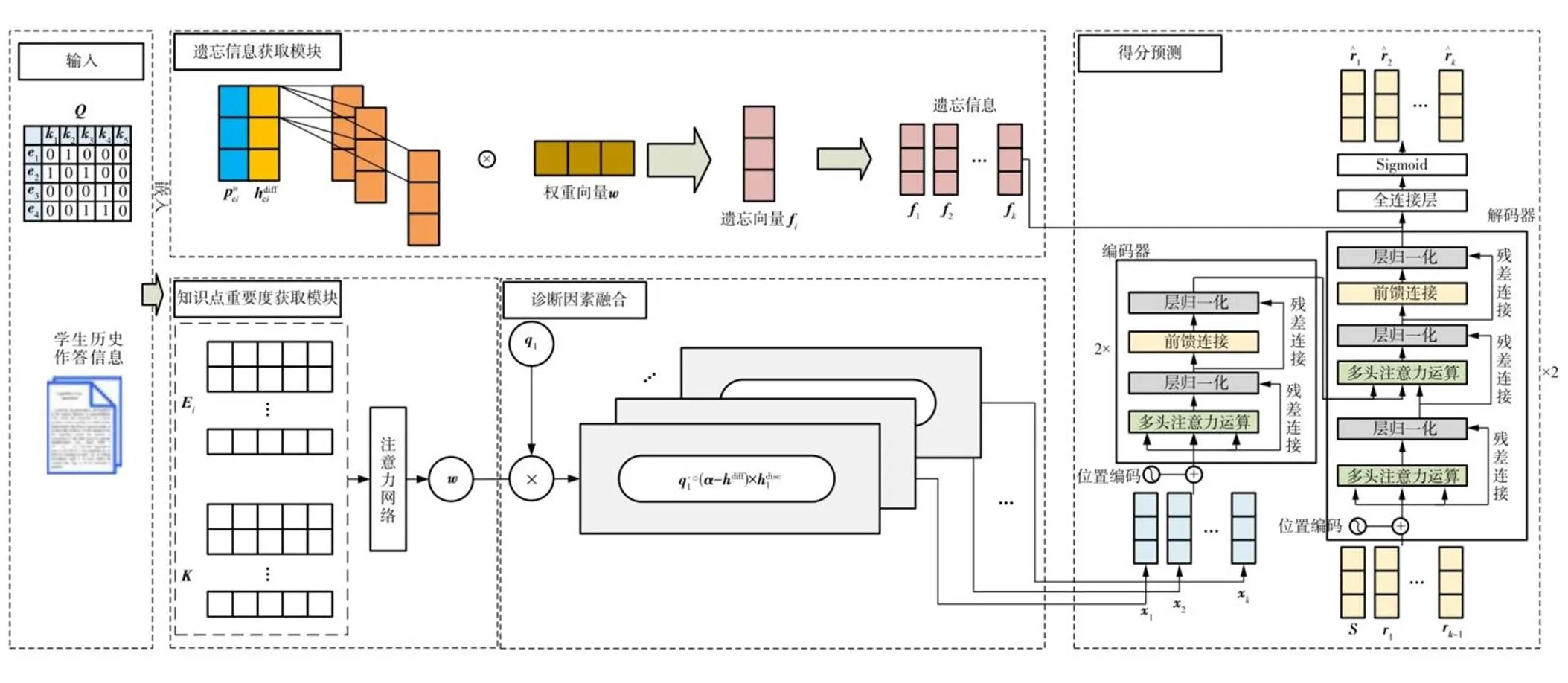
图2　FK-CD模型图

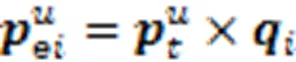
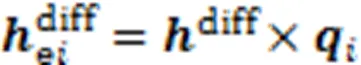
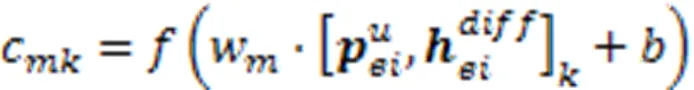
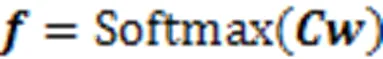
2.3　信息融合与得分预测模块

受到Wang等［11］的启发，文中在其融合方式基础上，对试题因素进行了更新，将含有知识点重要性的试题因素、学生因素、知识点难度因素和试题区分度等诊断因素进行融合，即

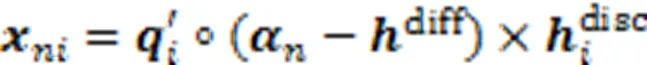
融合的结果可以作为对学生与试题交互信息的初步提取。为了获取更深层次的交互特征，提升诊断精确率，考虑到学生对试题交互的时序性影响，文中以Transformer网络结构为基础，在输入模块进行合理的设计，输出模块引入遗忘信息，生成预测得分。该网络模型包含输入、编码器、解码器和预测得分4个部分，如图2所示。

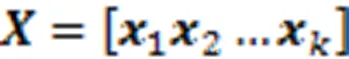
（2）位置编码。这里采用正余弦函数位置编码，即

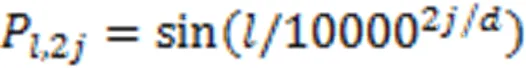
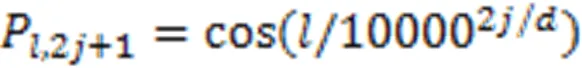
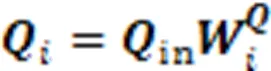
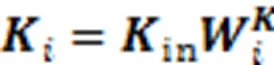
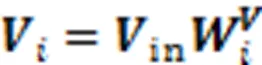
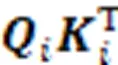
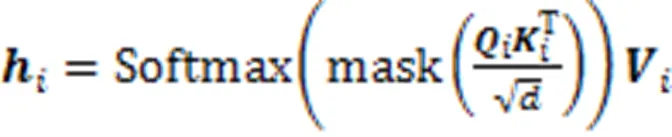
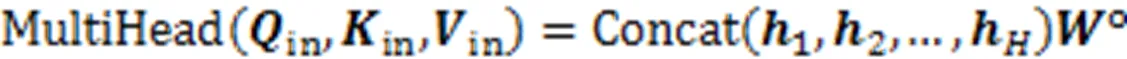
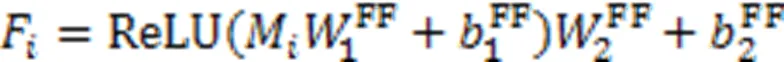
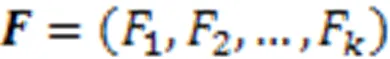
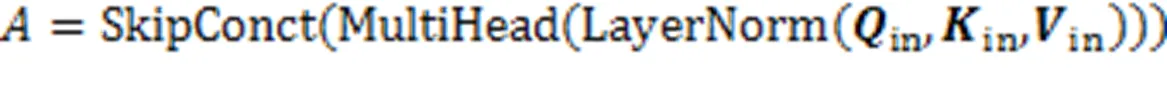
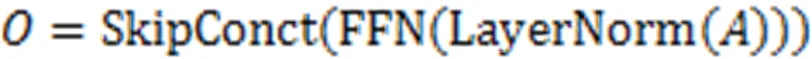
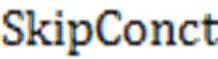
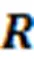
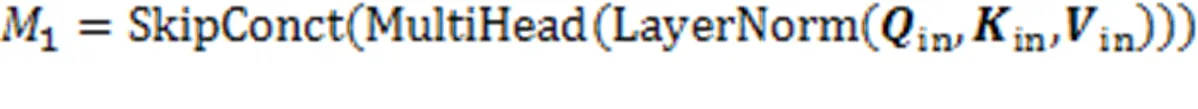
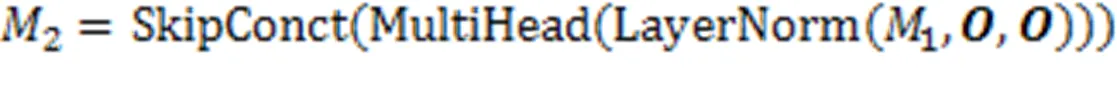
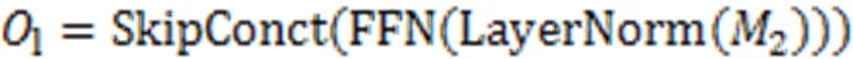
在最终的输出前，引入学生对试题的遗忘因素，经过一个线性变换层和Sigmoid层输出预测得分概率。

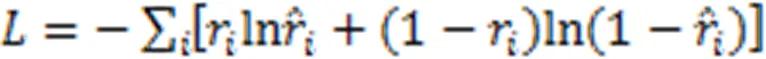
3　实验与结果分析

3.1　数据集

文中使用了教育领域的3个公开数据集，包括Assistment数据集［14］、Math1数据集和Math2数据集［15］。Assistment数据集是一个网上在线教学辅导系统收集到的小学生对数学练习题的作答记录，包含学生id、试题id、知识点id、交互时间和知识点名称等信息。Xiong等［16］针对数据重复问题将Assistment数据集进行了修正并公开。文中使用修正后的版本。Math1和Math2数据集是某个学校的髙中数学期末联考试题数据，包含学生试题交互数据和试题知识点关联矩阵。数据集的基本情况如表1所示。

表1　数据集概况

Table 1　Dataset overview

数据集学生数试题数知识点数作答记录试题平均知识点数 Assistment4 16317 746123324 5721.19 Math14 209151163 1353.20 Math23 911161662 5763.25

3.2　对比模型

为了评估文中模型的性能，将文中提出的FK-CD模型与传统模型、基于神经网络的模型进行比较，这些模型包括：

（1）PMF［17］模型，根据学生和试题的隐含特征进行得分预测；

（2）DINA［2］模型，使用二进制向量对学生的知识水平向量进行建模的认知诊断模型；

（3）IRT［3］模型，使用连续值为学生建模的一种认知诊断方法；

（4）MIRT［4］模型，使用多维能力为学生建模；

（5）DIRT［5］模型，使用深度学习提升IRT诊断效果，挖掘了问题文本的语义表示；

（6）NeuralCD［11］模型，使用神经网络获取学生与试题的交互函数，提升诊断精确度；

（7）IKNCD［18］模型，根据试题考查知识点次数，获取知识点自身重要度，改进神经认知诊断。

3.3　实验结果分析

文中通过准确率（cc）、均方根误差（RMSE）、受试曲线面积（AUC）、1指标分析模型的性能。8个模型在3个数据集上的实验结果如表2所示。Math1和Math2的数据量相对较小，Assistment数据集的数据量相对较大。从表中可以看出：文中模型在3个数据集上都取得了不错的效果；文中模型与IKNCD模型相比，在3个数据集上的cc和AUC分别提升了2.9%、2.8%、0.7%和2.2%、3.0%、1.7%，RMSE分别降低了0.7%、1.2%、1.1%。实验结果验证了FK-CD模型在学生成绩预测任务上的性能最优。

图3展示了8个模型在3个数据集上的1分数，从图中可以看出，文中模型的效果要优于其他模型，而且使用神经网络的模型效果明显优于传统模型，从而证明了利用神经网络的有效性。

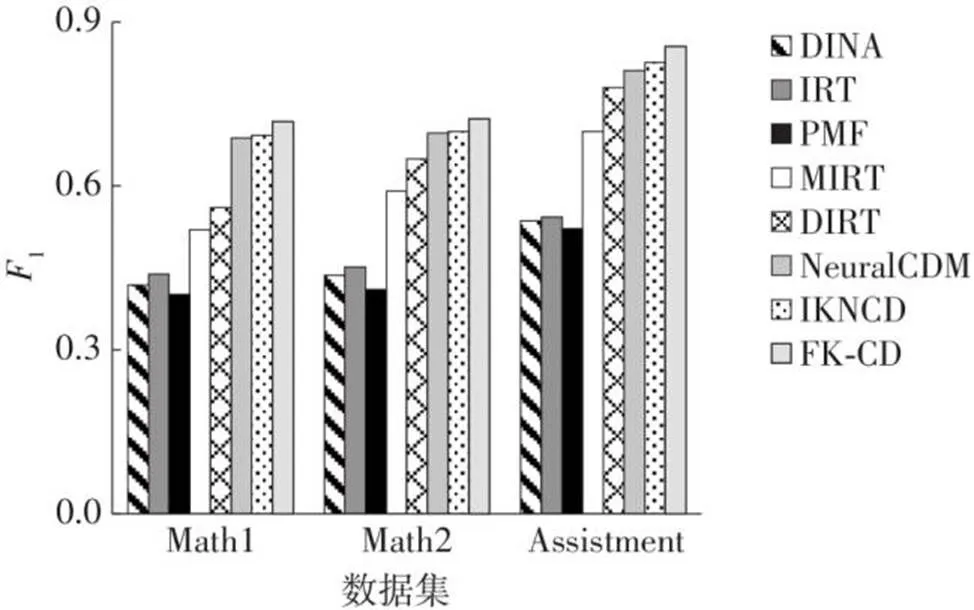
图3　8个模型在不同数据集上的F1值

3.4　消融实验

为了验证知识点重要度与学生遗忘对最终得分预测的影响，文中进行了消融实验，结果如表3所示。其中，F-CD表示仅考虑遗忘因素的影响而不使用Transformer网络，K-CD表示仅考虑知识点重要度因素的影响而不使用Transformer网络，FK-CDT表示考虑了遗忘因素和知识点重要度因素而不使用Transformer网络。从表中可以看出：在3个数据集上，F-CD、K-CD和FK-CDT相对于FK-CD的预测性能都有一些下降；在Math1和Math2数据集上，F-CD的性能下降较大，这可能是由于这两个数据集的数据量较小的原因。由此可以证明，增加知识点重要度和遗忘信息对预测结果有很大的影响，使用Transformer网络获取学生与试题的交互可以提升预测精度。

表2　8个模型的实验结果对比

Table 2　Comparison of experimental results among eight models

模型AccRMSEAUC Math1Math2AssistmentMath1Math2AssistmentMath1Math2Assistment DINA0.5930.5920.6500.4870.4750.4670.6860.6830.676 IRT0.6120.6100.6740.4800.4710.4640.7020.6990.685 PMF0.6050.6030.6590.4830.4720.4710.7010.6980.732 MIRT0.6230.6190.6930.4730.4660.4660.7070.7010.713 DIRT0.6360.6390.7050.4650.4650.4530.7170.7200.722 NeuralCD0.6770.6880.7190.4600.4540.4390.7400.7600.735 IKNCD0.6870.6970.7340.4520.4440.4380.7540.7770.762 FK-CD0.7160.7250.7410.4450.4320.4270.7760.8070.779

表3　消融实验结果

Table 3　Ablation experimental results

模型AccRMSEAUC Math1Math2AssistmentMath1Math2AssistmentMath1Math2Assistment F-CD0.6810.7030.7350.4530.4420.4380.7600.7810.767 K-CD0.6980.7070.7370.4490.4400.4370.7700.7870.767 FK-CDT0.6990.7100.7380.4490.4390.4350.7720.7890.769 FK-CD0.7160.7250.7410.4450.4320.4270.7760.8070.779

3.5　注意力模块的头数和层数对模型性能的影响

Transformer网络中，注意力部分可以通过设置不同头数和层数获取不同的结果。对这两个重要参数的不同选值进行实验分析，通过在3个数据集上的AUC值的比较，选取最合适的参数值，结果如图4所示。图中表明，本模型不需要深层的网络结构，在注意力模块层数为2时效果最佳，不同注意力模块头数的结果相差不大，8个头时效果最佳。

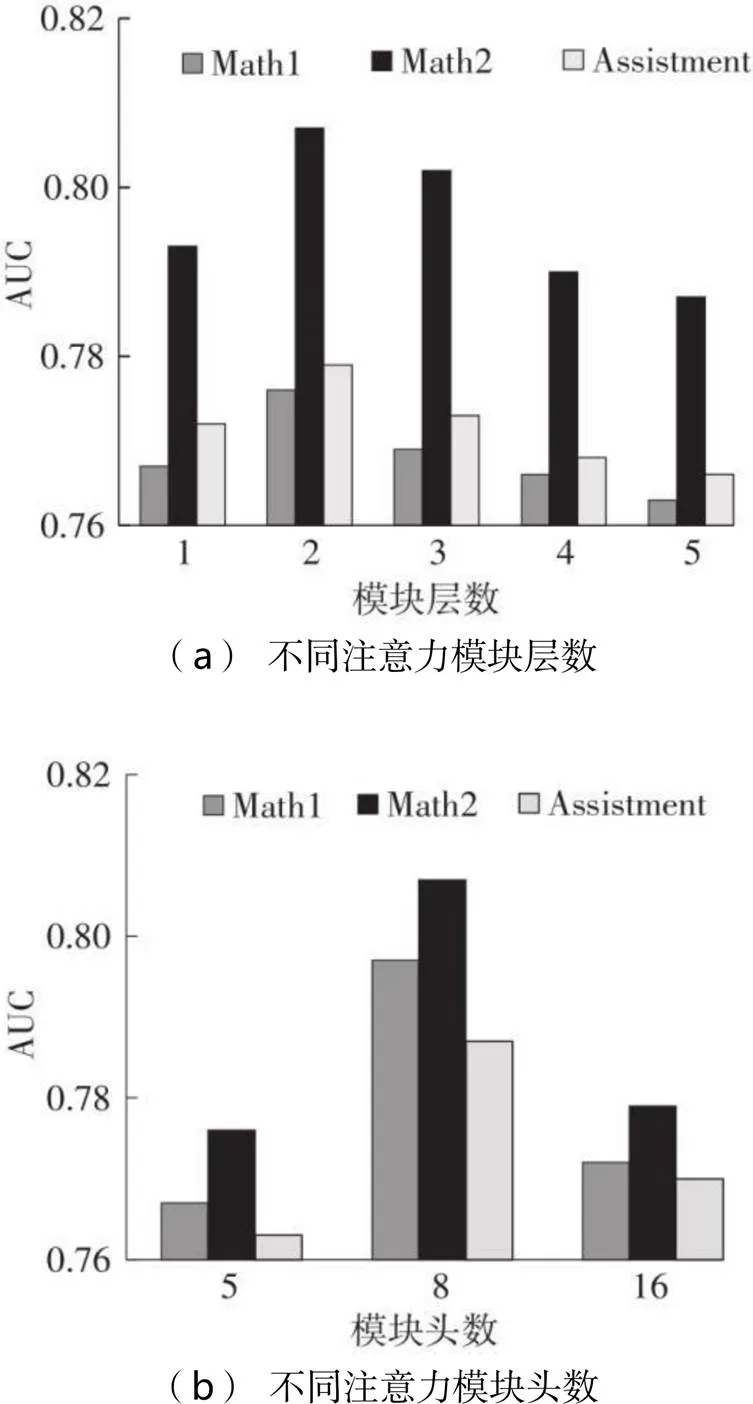
图4　不同注意力模块头数和层数时文中模型的AUC值

3.6　模型解释性实验

为了评估文中提出模型的可解释性，判断诊断结果是否合理，进行了模型解释性实验。根据实际经验，假设两个学生中如果学生相对于学生在知识点上的掌握程度更好，则学生相比于学生答对考查知识点的试题的可能性更大。为了验证文中提出的模型符合上述合理假设，采用一致性程度（DOA）［11］指标评估模型的可解释性。

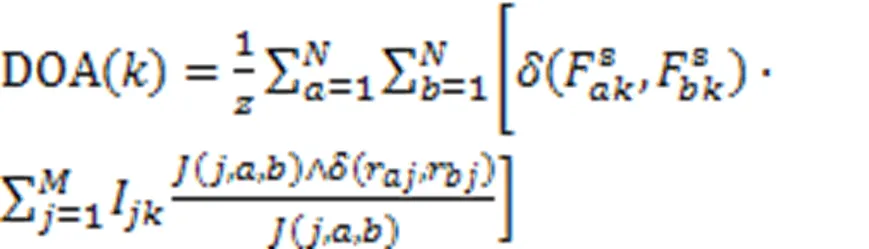
最后，对所有知识点的DOA求平均，得到模型的DOA值。DOA值代表学生对知识点的掌握程度比学生高的同时，学生对考查知识点的试题的答对率也高于学生的概率。DOA值越大，说明模型越好。

本次实验中，在3个数据集上都进行了模型的解释性实验，并将结果与NeuralCD和IKNCD模型进行对比，结果如表4所示。从表中可以看出，文中提出的FK-CD模型的DOA值在3个数据集上均高于NeuralCD和IKNCD模型的DOA值，这表明了FK-CD模型获取的学生知识掌握水平相对于NeuralCD和IKNCD两种模型更加合理和符合实际。

表4　在不同数据集上3个模型的DOA结果对比

Table 4　Comparison of DOA results among three models on different datasets

数据集DOA NeuralCDIKNCDFK-CD Math10.6670.6730.691 Math20.6170.6250.637 Assistment0.7950.8050.818

3.7　实例分析

为了验证文中提出方法的有效性，在Assistment数据集中选取了2名学生、3道试题还有与这3道试题相关的4个知识点。表5展示了试题和知识点的相关信息以及两名学生对各试题的作答情况。图5（a）为知识点难度雷达图，展示了融合试题-知识点考查重要度的知识点难度。图5（b）和图5（c）展示了通过FK-CD模型获取的两名学生的认知诊断结果，由于知识点难度、学生遗忘因素和学生先验知识点掌握程度的不同，表5中学生虽然答对了包含知识点“绝对值”“加法”“单位转换”“乘法”的题，但该学生对这些知识点的掌握程度并不相同，学生同理。

表5　试题对知识点的考查程度和学生作答结果

Table 5　Examination degree of knowledge points in the test questions and the results of students’ answers

知识点单位费率单位转换乘法绝对值加法学生a学生b 试题111000错对 试题201100对对 试题300011对错

理论上，当学生对试题考查的知识点的掌握水平高于试题考查知识点的难度时，学生更容易答对试题。例如，从图5中可以看出，试题1考查了知识点“单位费率”和知识点“单位转换”，并且两个知识点的难度分别为0.4和0.6，大于学生对这两个知识点的掌握程度0.1和0.4，小于等于学生对这两个知识点的掌握程度0.6和0.6，因此预测学生对试题1的作答结果为错，而预测学生对试题1的作答结果为正确，与表5中的实际作答结果相符。按此方法，从图5中可以看出，模型获得的学生的知识点掌握程度均符合预期结果。从而证明了FK-CD模型的有效性和可解释性。

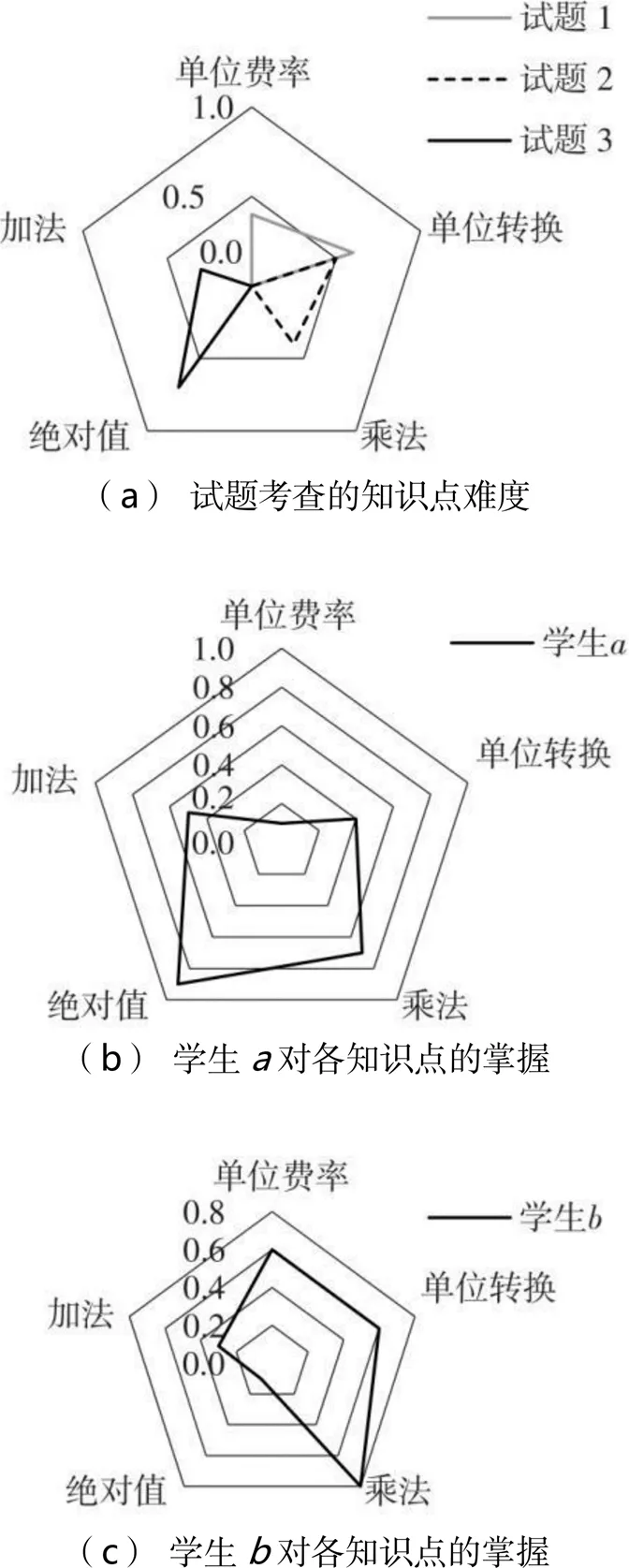
图5　试题知识点难度和学生对知识点的掌握雷达图

4　结语

针对认知诊断模型对学生和试题及其交互信息挖掘不充分的问题，文中提出了融合遗忘和知识点重要度的认知诊断模型，该模型考虑了学生在测试过程中每个人固有的遗忘特性和试题对知识点实际考查重要度对认知诊断模型得分预测结果产生的重要影响；设计了获取学生遗忘因素和知识点考查重要度因素的方法，将各因素融合并通过Transformer网络来获取学生与试题的交互信息，以提升诊断结果。实验结果表明，在Math1、Math2、Assistment数据集上的准确率cc、均方根误差RMSE、受试曲线面积AUC值分别为0.716、0.445、0.776、0.725、0.432、0.807、0.741、0.427和0.779。

文中用到的试题知识关联矩阵由专家标记，这费时费力，精确度也不一定高。随着深度学习的发展，可以利用深度学习方法对进行改进，将机器标注与专家标注相结合，以获得更加精确的矩阵，提高认知诊断精确度。

［1］ NICHOLS P D，JOLDERSMA K．Cognitive diagnostic assessment for education：theory and applications［J］．Journal of Educational Measurement，2008，45（4）：407- 411．

［2］ TORRE J．DINA model and parameter estimation：a didactic［J］．Journal of Educational and Behavioral Statistics，2009，34（1）：115-130．

［3］ EMBRETSON S E，REISE S P．Item response theory［M］．London：Psychology Press，2013： 56-87．

［4］ RECKAS M．Multi-dimensional item response theory［J］．Handbook of Statistics，2009，26（6）： 607-642．

［5］ CHENG S，LIU Q，CHEN E，et al．DIRT：deep learning enhanced item response theory for cognitive diagnosis ［C］∥ Proceedings of the 28th ACM International Conference on Information and Knowledge Management．Beijing：ACM，2019：2397-2400．

［6］ ZHU T，LIU Q，HUANG Z，et al．MT-MCD：a multi-task cognitive diagnosis framework for student assessment ［C］∥ Proceedings of the 23rd International Conference on Database Systems for Advanced Applications．Gold Coast：Springer，2018：318-335．

［7］ LIU Q，WU R，CHEN E，et al．Fuzzy cognitive diagnosis for modelling examinee performance［J］．ACM Transactions on Intelligent Systems and Technology，2018，9（4）：48/1-26．

［8］ XU J，LI Q，LIU J，et al．Leveraging cognitive diagnosis to improve peer assessment in MOOCs［J］．IEEE Access，2021，9：50466-50484．

［9］ PIECH C，BASSEN J，HUANG J，et al．Deep knowledge tracing［C］∥ Proceedings of the 28th International Conference on Neural Information Processing Systems．Cambridge：MIT Press，2015：505-513．

［10］ GIERL M J，CUI Y，HUNKA S．Using connectionist models to evaluate examinees’ response patterns to achievement tests［J］．Journal of Modern Applied Statistical Methods，2008，7（1）：234-245．

［11］ WANG F，LIU Q，CHEN E，et al．Neural cognitive diagnosis for intelligent education systems ［C］∥ Proceedings of the 34th AAAI Conference on Artificial Intelligence．Menlo Park：AAAI，2020：6153-6161．

［12］ 李晓光，魏思齐，张昕，等．LFKT：学习与遗忘融合的深度知识追踪模型［J］．软件学报，2021，32（3）：818-830．

LI Xiao-guang，WEI Si-qi，ZHANG Xin，et al．LFKT：deep knowledge tracing model with learning and forgetting behavior merging［J］．Journal of Software，2021，32（3）：818-830．

［13］ HUANG Z，LIU Q，CHEN Y，et al．Learning or forgetting？ A dynamic approach for tracking the knowledge proficiency of students［J］．ACM Transactions on Information Systems，2020，38（2）：19/1-33．

［14］ WU R，LIU Q，LIU Y，et al．Cognitive modelling for predicting examinee performance ［C］∥ Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence．Buenos Aires：AAAI，2015：1006-1097．

［15］ FENG M，HEFFERNAN N，KOEDINGER K．Addressing the assessment challenge with an online system that tutors as it assesses［J］．User Modeling and User-Adapted Interaction，2009， 19（3）：243-266．

［16］ XIONG X，ZHAO S，Van INWEGEN E G，et al．Going deeper with deep knowledge tracing［C］∥Proceedings of the 9th International Conference on Educational Data Mining．Raleigh：International Educational Data Mining Society，2016：545-550．

［17］ SALAKHUTDINOV R，MNIH A．Probabilistic matrix factorization［C］∥ Proceedings of the 20th International Conference on Neural Information Processing Systems．Red Hook：Curran Associates Inc．，2008：1257-1264．

［18］ CHENG Y，LI M，CHEN H，et al．Neural cognitive modeling based on the importance of knowledge point for student performance prediction［C］∥ Proceedings of 16th International Conference on Computer Science & Education．Lancaster：IEEE，2021：495-499．

Cognitive Diagnosis Model Integrating Forgetting and Importance of Knowledge Points

（School of Computer Science and Technology，Harbin University of Science and Technology，Harbin 150001，Heilongjiang，China）

Intelligence education is the key research direction of artificial intelligence. The most important is to describe the students’ cognitive process by ultilizing the knowledge points in the test questions. Aiming at the problem that the cognitive diagnosis model is insufficient for mining students, test questions and their interactive information, this study proposed a cognitive diagnosis model integrating forgetting and the importance of knowledge points. According to the historical interaction between the test questions and knowledge points, the model introduces forgetting factors in combination with the difficulty information of knowledge points, thus alleviates the problem of insufficient information mining for students. Through the attention mechanism, the importance information of the test questions to the knowledge points was obtained to alleviate the problem of insufficient information mining of the test questions. Learning the interaction relation between students and test questions through Transformer alleviates the problem of insufficient interaction information between students and test questions. The results of experiments carried out on the classic dataset show that the accuracycc, root mean square error (RMSE), and the area under curve (AUC) values of this method on the Math1, Math2, and Assistment datasets are 0.716, 0.445, 0.776, 0.725, 0.432, 0.807, 0.741, 0.427, 0.779, respectively. Compared with other existing models, the proposed method has better results. The proposed method illustrates the importance of knowledge importance and timeliness for cognitive modeling.

cognitive diagnosis；attention mechanism；transformer；importance of knowledge points；forgetting information

Supported by the National Natural Science Foundation of China （62172128，61300115） and the China Postdoctoral Science Foundation （2014m561331）

10.12141/j.issn.1000-565X.220279

2022⁃05⁃16

国家自然科学基金资助项目（62172128，61300115）；中国博士后科学基金资助项目（2014m561331）；黑龙江省教育厅科学技术研究项目（12521073）

刘宇鹏（1978-），男，博士，教授，主要从事自然语言处理、智能教育、认知计算研究。E-mail： flyeagle99@126.com

TP391

1000-565X（2023）05-0054-09