基于MIKE耦合模型的典型平原感潮河网地区排污口水环境影响研究
2023-06-29段志强徐心彤胡祉冰徐若诗
段志强,逄 勇,徐心彤,胡祉冰,徐若诗
(1.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏 南京 210098;2.河海大学环境学院,江苏 南京 210098;3.浙江省环境科技有限公司,浙江 杭州 310000)
0 引言
长江经济带作为新时期国家区域发展格局的重中之重,依托长江黄金水道,是我国涵盖面最广、影响最大、与生态可持续发展息息相关的黄金经济带[1-2]。改革开放以来,长江流域社会经济持续高速发展,以经济发展为导向的资源过度利用型开发模式忽视了资源可持续利用和生态环境保护的重要性,区域协调发展受到严重制约[3-5]。 长江三角洲为典型的平原感潮河网地区,河网纵横交错,受潮汐和径流的影响,水流状态复杂[6],且周围沿江城市密集,污染物入河量大而集中,城市河道水动力条件较弱、水环境容量较小[7],区域资源环境的压力进一步增大。 而入河排污口是陆源污染负荷从岸上到河里的关键枢纽,通过数值模拟分析论证排污口设置,预测尾水中污染物的迁移转化及扩散趋势,对于流域生态环境保护具有重要意义[8]。
目前针对入河污染物排放水环境影响的研究一般采用数值模拟软件,主要包括QUAL,EFDC,WASP,SWAT,MIKE 模型等[9-14]。 其中MIKE 系列模型因其模拟精度高且综合性强,在水环境数值模拟中得到广泛应用。王天泽等[15]将MIKE11 与MIKE21通过MIKE FLOOD 进行耦合,建立了城市暴雨洪水模型,模拟了现状河道和规划河道在不同条件下的洪水演进过程和淹没风险;王浅宁等[16]利用MIKE耦合一维管网模型和地表漫流二维模型,对洪涝灾害和超标准洪水应对进行分析;陈平等[17]建立MIKE一维及二维耦合的南澧河及两岸保护区的水动力模型,并对100 a 一遇的洪水演进过程进行风险要素分析;栾震宇等[18]利用MIKE URBAN-MIKE21 耦合模型对湖南省新化县的城市内涝情景进行模拟,并对地表漫流、城市易涝点和管道排水能力进行分析;李明等[19]基于MIKE11,ECO Lab 模块及MIKE SHE构建了沙河水库流域水动力及水质耦合模型,模拟污染物的迁移转化,进而探究河道水质的改善方案。目前,MIKE 耦合模型在城市内涝和洪水演进的水动力模拟中应用广泛,但是对于感潮河网地区的水质模拟研究较少。
本文以COD,NH3-N 和TP 为目标污染物,应用MIKE11 及MIKE21 模型的水动力模块及对流扩散模块,构建了泰兴市感潮河网地区一维及长江泰兴段二维耦合的水动力-水质模型,模拟泰兴市某工业园区拟建入河排污口在不同工况下尾水中多元污染物在长江中的迁移转化,计算不同潮汐状况下污染带的扩散范围,分析污染物排放对长江水环境的影响。
1 研究区域概况
泰兴市地处长三角洲冲积平原,南临长江,受季风和潮汐的影响显著,属典型的平原感潮河网地区,河流纵横交织,水网密布,以人工河渠为主,河流水位、流向、流速大多受到节制闸控制,另有部分天然洼地积水成条形或不规则水面,与人工河道沟通。区内及周边主要河道包括长江(泰兴段)、靖泰界河、天星港、焦土港、六圩港等。
泰兴市某工业园区拟建排放规模为2 万t/d 污水处理厂,拟设置入河排污口在六圩港,尾水经五圩港、六圩港后最终汇入长江,研究区域概况见图1。

图1 研究区域概况
2 研究方法
2.1 模型方程
2.1.1 河网模型
水动力基本方程是基于流量和水位交替网格的六点Abbott-Ionescu 隐式有限差分法求解的建立在质量和动量守恒定律基础上的一维非恒定Saint-Venant 方程组,以流量Q(x,t)和水位Z(x,t)为未知变量,方程组为:
式中:Q 为流量;x 为沿水流方向空间坐标;Bw为调蓄宽度,包括滩地在内的全部河宽;z 为水位;t 为时间;q 为旁侧入流流量,入流为正,出流为负;u 为断面平均流速;g 为重力加速度;A 为主槽过水断面面积;B 为主流断面宽度;n 为糙率;R 为水力半径。
河网对流传输的基本方程为:
式中:Ex为x 方向扩散系数;C 为模拟物质的浓度;Sc为与模拟物质浓度有关的衰减项,Sc=Kd·A·C;Kd为衰减因子;S 为源项。
2.1.2 长江模型
二维水动力控制方程是基于三向不可压缩和雷诺值均布的Navier-Stokes 平均方程沿水深方向积分的连续方程和动量方程,服从Boussinesq 及静水压力假定,其二维非恒定浅水方程组如下[20]:
连续方程:
动量方程:
式中:x,y 为Cartesian 坐标;h=η+d,h 为总水深,η为水位,d 为静水深;ρ 为水体密度;u 和v 为x,y 方向上速度分量;f=2 ωsinφ;表示Coriolis 因子(ω 是地球自转的角速度,φ 是地理纬度);Sxx,Sxy和Syy为辐射应力分量;Pa为大气压;us和vs为点源速度分量;Tij为横向应力,包括粘滞力、紊流应力及水平对流摩擦力。
污染物在二维非均匀流中的对流扩散基本方程可以表示为:
式中:Ey为y 方向的扩散系数;Sk为动力转换项。
2.2 耦合模型构建
一维河网模型计算范围包括六圩港、五圩港、连复港、涌兴港。 根据典型年研究区域内长江涨、落潮水利工程的调度资料及边界处在90%枯水保证率条件下的水位和流量确定边界水文条件。 以安浩[21]建立的里下河腹部区一维河网模型水动力率定结果为基础,设置河道糙率为0.026。 根据长江实测水下地形数据,建立二维长江马鞍山~高桥段及泰兴段模型。 其中长江泰兴段模型平均网格边长约300 m,网格总数为1 545 个,局部加密段网格边长约为50 m,二维模型计算范围及水下地形见图2。 初始水位取水文年鉴资料平均水位2.5 m,起始时刻流速设为0。 设置长江下游段主槽糙率的取值范围为0.01~0.02,风拖曳系数为0.001 ~0.001 5,横、纵向扩散系数分别为0.6 m2/s,60 ~120 m2/s,研究区域内COD,NH3-N,TP 等污染物降解系数见表1。

表1 研究区域污染物综合降解系数
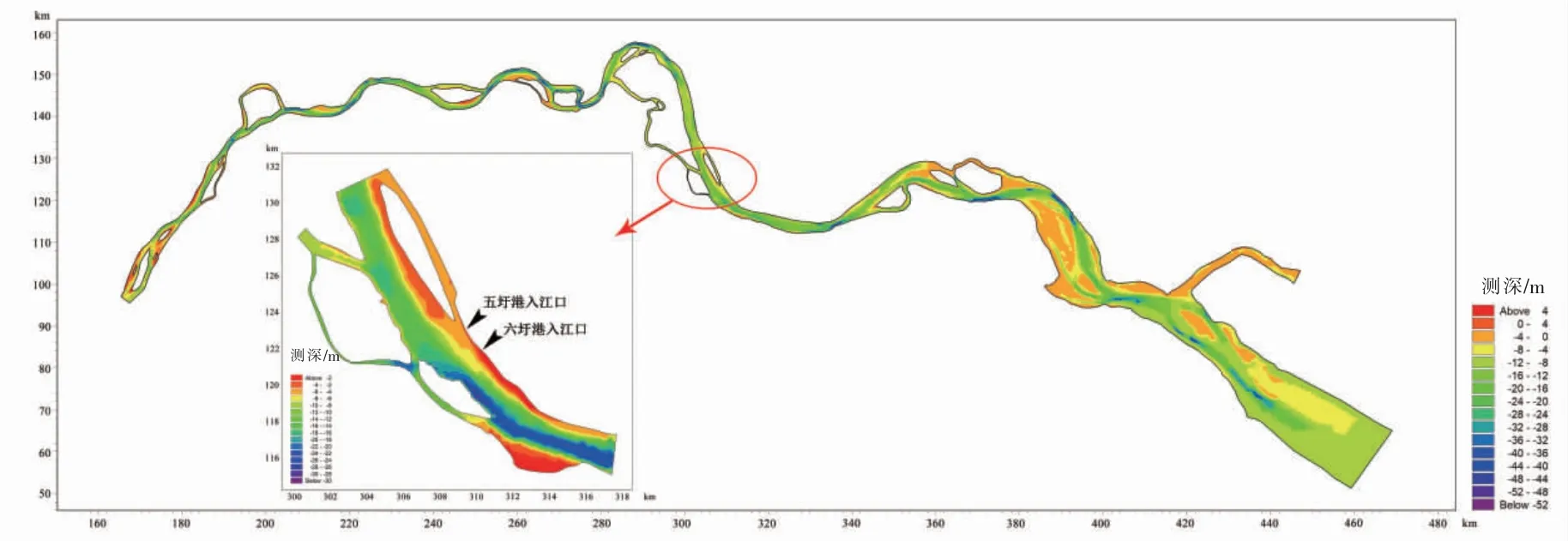
图2 长江模型计算范围及水下地形
根据一、 二维模型连接处动量守恒的原理采用标准连接,对河网模型及长江模型进行动态耦合。一、 二维的耦合根据流量与水位在连接断面处相同的条件,由一维河网计算出连接河道末端的流量及水质浓度数值作为二维连接网格处的源项,二维模型计算的网格点水位及水质浓度数值以入流边界的形式提供给一维河网模型的衔接点。 在衔接处的河网端点处给定一个虚拟的水位边界,并且用作耦合模型的启动边界[21-22],耦合模型网格划分见图3。
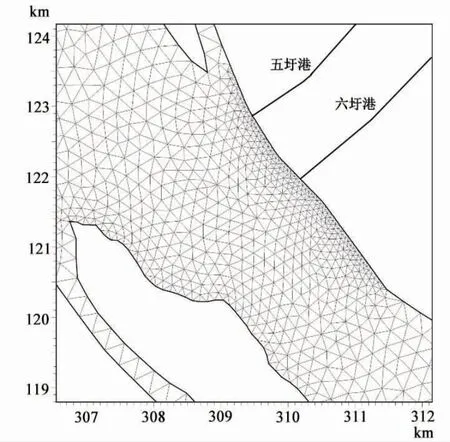
图3 一、二维耦合模型网格划分示意
2.3计算方案
根据建立的区域河网-长江泰兴段水环境耦合模型,结合长江口潮汐特征,在设计水文条件下,泰兴市某工业园区污水处理厂建成投运后,分别以正常、 事故工况下尾水排放后五圩港及六圩港入江口水质浓度作为长江模型污染源,分析尾水中COD,NH3-N 和TP 在涨急、 落急时刻释放对长江水环境的影响,预测方案见表2。

表2 预测方案及污染物源强信息
3 结果与讨论
3.1 模拟结果评价
根据2015年10月15日~22日南京站、 镇江(二)站、江阴站、营船港站感潮水位数据对耦合模型水位模拟结果进行率定,各水文站的水位模拟结果与实测值对比结果见图4。 根据Nash-Sutcliffe 效率系数Ens、 相对误差RE 和判定系数R2验证模型精度,计算得出Ens为0.910,RE 为5.8%,R2达到0.903,且一般认为,Ens≥0.5,R2≥0.6 时模拟结果较可靠[19,24],故本次建立的耦合模型可较好的适用于研究区域的水动力模拟。

图4 各站点水位模拟值与观测值对比
研究选择2015年10月17日~19日长江镇江(二) 站至徐六泾站之间各水源地COD,NH3-N 和TP 的同步观测数据对水质模型计算结果进行率定。 根据百分比偏差PBIAS 对水质模拟结果进行评价[19,25,26],其中COD 平均偏差为3.86%,NH3-N 平均偏差为20.06%,TP 平均偏差为18.15%,模拟误差PBIAS ≤25%,模拟结果优秀。各断面水质模拟结果与实测值对比见图5。
3.2 入江口水质浓度预测
不同工况下六圩港、 五圩港入江口水质浓度见表3。 由表3 可以看出,正常工况条件下,污水处理厂尾水经五圩港、六圩港汇入长江,各污染物浓度增量叠加水质现状监测数据后,排污口下游2 条入江河流入江口处断面水质均达到地表水Ⅲ类标准,其中六圩港入江口COD,NH3-N,TP 质量浓度增量分别为0.9,0.05,0.005 mg/L; 五圩港入江口处污染物质量浓度增量分别为0.7,0.05,0.005 mg/L。 事故工况条件下,污水厂尾水进入受纳水体六圩港,2 条入江河流入江口断面水质均超过GB 3838—2002 《地表水环境质量标准》中相应限值,其中六圩港COD,NH3-N,TP 质量浓度增量为13.5,1.01,0.17 mg/L,超标倍数分别为0.575,0.69,0.75; 五圩港质量浓度增量分别为12.8,0.91,0.133 mg/L,超标倍数分别为0.495,0.77,0.6。 模拟结果表明,相同工况下,同种污染物对2 条入江河流入江口断面产生的质量浓度增量相近,这主要是因为2 条入江河道流量及流速几乎相同;事故工况时污染负荷较高的尾水导致入江口处污染物浓度增量增大,入江污染物通量显著增加。

表3 各工况下六圩港、五圩港入江口污染物浓度mg·L-1
3.3 潮汐作用下的污染物影响范围
为研究不同潮汐条件下各类污染物扩散对长江水环境的影响,通过耦合模型计算得到不同工况下污水厂尾水中多元污染物在长江涨急、 落急时刻的浓度增量扩散范围。预测影响范围见图6 和图7。由图6 和图7 可以看出,不同工况下的污染带范围存在明显差异。
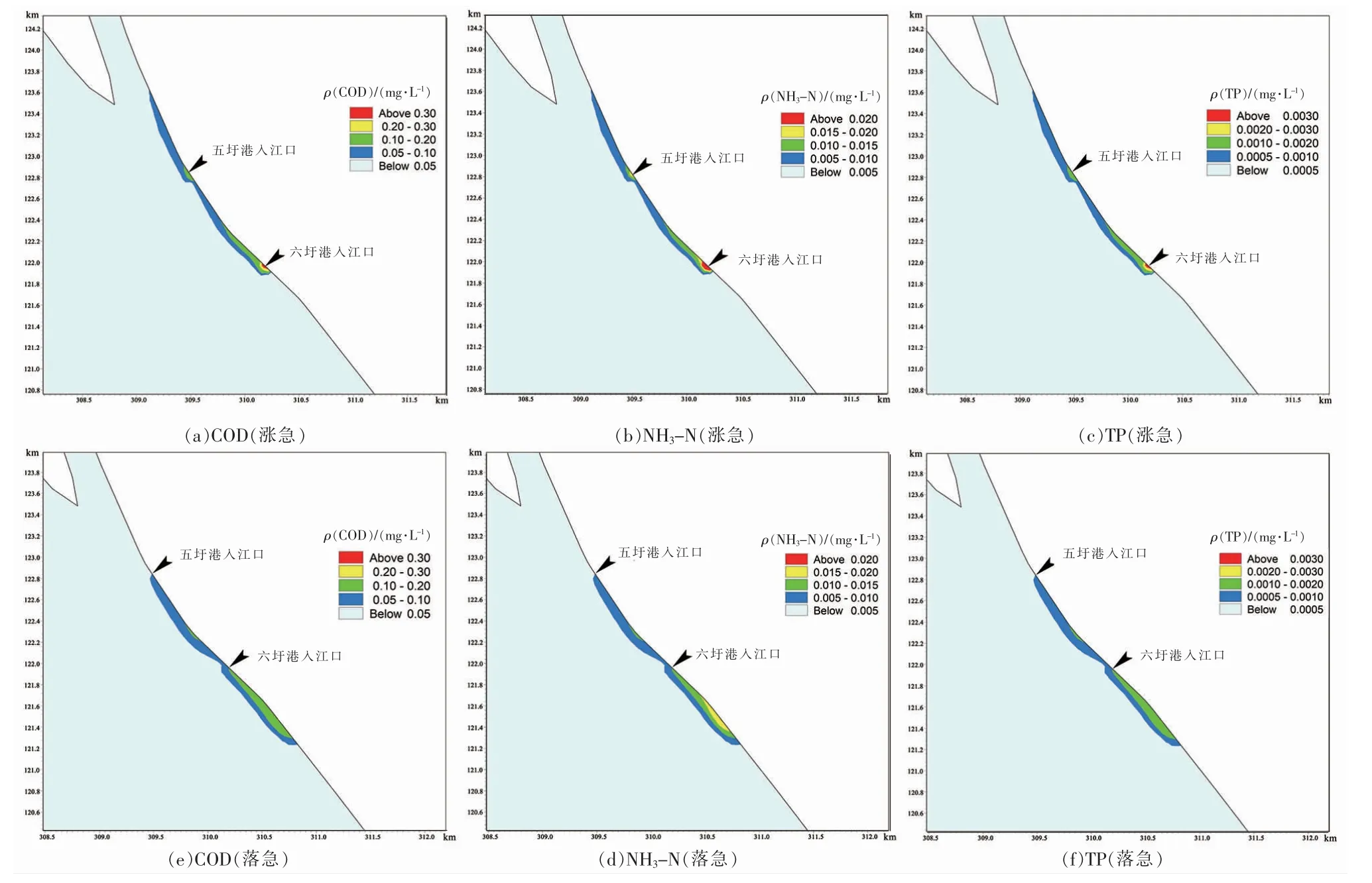
图6 正常工况TCOD,NH3-N,TP 浓度增量影响范围
图7 事故工况下COD,NH3-N,TP 浓度增量影响范围
正常工况时,COD,NH3-N,TP 超过背景浓度的横向扩散影响距离分别为150,100,111 m,涨急时纵向扩散影响距离分别为2 100,2 105,1 778 m,落急时纵向扩散影响距离分别为1 864,2 167,2 160 m。其中,涨急时,COD 质量浓度增量超0.3 mg/L 的面积为4 508 m2,占比1.74%,入江口处污染物质量浓度增量最高,在潮水向上顶托的作用下向上游迁移扩散,六圩港入江口形成的污染带中COD 质量浓度增量由入江口0.34 mg/L 下降至0.052 mg/L,其他污染物浓度分布规律相似;落急时,污染带中COD 质量浓度增量均未超过0.3 mg/L,六圩港入江口COD质量浓度增量由0.12 mg/L 下降至0.056 mg/L。 可见,污水厂正常排放后形成的污染带范围较小,涨潮期间水流向上流动不利于污染物输移扩散,污染物浓度较高的区域相对于落潮时增大。
事故工况时,随着污水厂排污负荷增大,入江口污染物浓度相应升高,五圩港、六圩港入江口污染物扩散叠加后的复合污染带纵向影响范围有所增大,而横向扩散距离略有减小。涨急时,COD,NH3-N,TP超过背景浓度的纵向扩散影响距离分别增长122,673,440 m,其中COD 质量浓度增量基本超过0.3 mg/L,超1.0 mg/L 的面积为85 964 m2,在污染带中占比35.7%; 落急时超过背景浓度的纵向扩散影响距离分别增长136,7,129 m,其中COD 质量浓度增量超1.0 mg/L 的面积在污染带中占比为32.6%。可见,污水厂尾水事故排放后,入江污染物通量的增加使污染物浓度较大的区域占比增大,对污染物扩散范围影响较大,污染带随排污量的增加而持续伸长,对长江水环境有一定程度的影响,应加强污水厂运行管理,避免事故的发生。
对比2 种方案下污染物在涨、 落潮的扩散情况可知,泰兴市某工业园区污水厂拟设排污口尾水正常排放时,污染物排放浓度最低,污染带范围较小,对长江水生态环境影响范围、 影响程度最小; 涨急时,污染物随潮水向上游迁移扩散,五圩港、六圩港入江口处形成的复合污染带有明显上溯趋势,上游污染带长度相对较长,污染物扩散对上游水环境影响较大;落急时,污染物扩散带向下游延伸,最远可至六圩港入江口下游1.05 km;对于同一入江口处形成的污染带,各污染物浓度随纵向距离增加而逐渐削减,污染物高浓度区域比例随入江污染物通量的增加而增大。
4 结论
本文以长江三角洲典型平原感潮河网地区泰兴市为例,分析了长江感潮河段在污水处理厂正常、事故工况下尾水排放对长江水生态环境的影响。
(1)建立泰兴市感潮河网-长江的水动力-水质耦合模型,并用2015年水文水质数据进行率定验证,水动力模拟Ens,RE,R2分别为0.910,5.8%,0.903,水质模拟误差PBIAS 小于25%,耦合模型精度较高,可较好的适用于计算区域内COD,NH3-N,TP 等污染物的迁移转化模拟。
(2)新建排污口对入江口断面产生浓度增量,六圩港入江口COD,NH3-N,TP 质量浓度正常排放时分别新增0.9,0.05,0.005 mg/L,事故排放时分别新增13.5,1.01,0.17 mg/L,污染物入江通量随污水厂排污负荷的增加而增大。
(3)涨、落潮等水流情势及污染物入江负荷的变化均会对长江污染带扩散产生一定影响。 污染带扩散趋势与水流方向相一致。污水厂尾水正常排放时,污染带范围较小;事故排放时,随着入江污染物通量的增加,污染物高浓度区域范围增大,对长江水质影响较大,因此应加强污水处理厂的运行管理,各类污水达标排放,杜绝引入污染负荷较高的尾水。
