在线优化参数的多变量非线性预测函数控制

侯小秋

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

多变量非线性控制是一个广泛的问题,周瑞敏等[1]给出了基于对角递归神经网络优化的PID控制算法。耿睿等[2]提出一种非线性未建模动态与线性模型相组合的集成模型,采用BP神经网络辨识未建模动态项,设计了多变量非线性广义预测控制。黄帅等[3]研究非线性多变量系统的多模型自适应控制,控制方法由神经网络自适应控制器与线性自适应控制器切换组成。姜雪莹等[4]给出基于RBF神经网络的多变量非线性内部迭代预测控制算法。文献[1-4]为非线性多变量控制的最新研究,但不是关于实用随机多变量NARMAX模型的控制研究。侯晓秋等[5]分析随机NARMAX模型中随机干扰量在模型中描述的形式难以确定的问题,将随机干扰量从函数中分离出来,等效在模型的输出端,基于滤波器提出实用随机NARMAX模型。侯小秋[6]研究其可克服算法病态的非线性递推最小二乘法,提出其在线修正参数的预测滤波PID控制算法。侯小秋[7]提出实用随机多变量NARMAX模型,给出可克服算法病态的多变量非线性递推最小二乘法进行参数估计,未研究其控制问题。笔者研究其在线优化输入输出加权系数的多变量非线性预测函数控制算法。

1 改进随机多变量NARMAX模型

1.1 实用随机多变量NARMAX模型

文献[7]提出的实用随机多变量NARMAX模型为

y(t+d)=F[Y(t+d-1),Y(t),

u(t),U(t-1),θ]+ω(t+d),

(1)

式中:y(t)——输出向量;

u(t)——输入向量;

d——时滞;

θ——待估参数集合;

ω(t)——随机干扰向量;

F(…)——向量函数。

YT(t+d-1)=[y(t+d-1),

y(t+d-2),…,y(t+1)],

YT(t)=[y(t),

y(t-1),…,y(t-ny)],

UT(t-1)=[u(t-1),

u(t-2),…,u(t-nu)]。

干扰模型

(2)

且

C(q-1)=I+C1q-1+…+Cncq-nc,

式中:e(t)——白噪声向量;

I——单位矩阵;

C1(q-1)——矩阵多项式;

A(q-1)——矩阵多项式;

q-1——单位后移算子。

1.2 参数估计

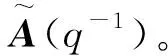
1.3 时变多变量CARMAX模型的逼近

将文献[5]的四个假设条件和时变CARMAX模型逼近方法推广到多变量情形。

动态工作点为

y0(t+d-2),…,y0(t+1)],

u0(t)=[u10(t),u20(t),…,un0(t)],

y0(t+d-1)=y0(t+d-2)=…=y0(t+1)=y0(t)。

y0(t)和u0(t)可表示为

y0(t)=(I-α)y0(t-1)+αy(t),

u0(t)=(I-β)u0(t-1)+βu(t-1),

式中:α=diag[α1,α2,…,αn],0≤αi≤1,i=1,2,…,n;β=diag[β1,β2,…,βn],0≤βi≤1。

对式(1)在动态工作点处一阶泰勒展开,采用动态切平面逼近

y(t+d)=F[Y0(t+d-1),Y(t),u0(t),

i)-y0(t+d-i)]+φu(t)[u(t)-

u0(t)]+ω(t+d),

整理得:A(q-1)y(t)=q-dφu(t)u(t)+

D(t)+ω(t),

(3)

D(t)=F[Y0(t+d-1),Y(t),u0(t),U(t-1),θ]-

(4)

A(q-1)=I+A1q-1+…+A(d-1)q-(d-1),

且Ai=φyi(t)。

由式(4)可知,D(t)在t时刻已知,将式(2)代入式(3)得

C(q-1)e(t),

(5)

2 递推预测模型

式(5)忽略噪声项C(q-1)e(t),可得

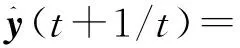
(6)

由式(5)、(6)可得

(7)

由式(7)递推可得:

(8)

(9)

(10)

(11)

将式(9)～(11)代入式(8)得

yf(t+d+j),

(12)

式中,yf(t+d+j)——自由响应。

由式(12)令j=0,1,…,p,整理矩阵形式为

(13)

UT(t)=[uT(t),uT(t+1),…,uT(t+p)],

3 预测函数控制

3.1 基函数的选取

控制器算法为

i=0,1,…,p;l=1,2,…,n,

(14)

式中:μl,k(t)——加权系数;

fl,k(i)——基函数在t+i时刻的值;

Nl——基函数的维数;

n——系统维数。

3.2 参考轨迹

yr(t+i)=r(t+i)-γi[r(t)-yp(t)],

式中:yr(t+i)——参考轨迹向量;

r(t)——设定值向量;

yp(t)——实际输出向量;

γ——衰减因子矩阵。

yr,n(t+i)],

rT(t)=[r1(t),r2(t),…,rn(t)],

γ=diag[γ1,γ2,…,γn]。

3.3 预测误差校正

预测误差向量为

i=0,1,…,p,

校正的预测输出向量

j=d,d+1,…,d+p,

式中,ym(t+j)——校正的预测输出向量。

矩阵形式为

(15)

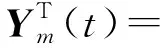
3.4 预测函数控制算法

将式(14)整理成矩阵形式为

(16)

式中:μT(t)=[μ1,1,μ1,2,…,μ1,N1,

μ2,1,μ2,2,…,μ2,N2,…,

μn,1,μn,2,…,μn,Nn],

目标函数为

(17)

式中:ρ(t)——输出加权对角矩阵;

λ(t)——输入加权对角矩阵;

ρ(t)=diag(ρ1,ρ2,…,ρn×(p+1)),

λ(t)=diag(λ1,λ2,…,λw)。

由式(15)(13)可得

(18)

式(18)的矩阵求逆使用文献[7]的算法计算。

4 梯度表达式

输入输出加权对角矩阵ρ(t)和λ(t)影响系统稳定性和鲁棒性,文中对其在线优化,控制算法可调参数向量为

ηT=[ρ1,ρ2,…,ρn×(p+1),λ1,λ2,…,λw],

则

式(18)对ρi求偏导

(19)

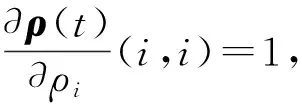
(20)

将式(18)对λi求偏导得:

(21)

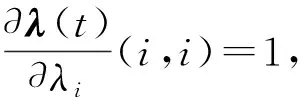
(22)

将式(16)对ηi求偏导

(23)

式(13)对ηi求偏导

(24)

式(15)对ηi求偏导

(25)

5 在线优化参数

文献[6]改进目标函数为

式中:μ——遗忘因子;

τj——加权因子;

λη(t)——权重对角矩阵;

εj(i,η)=ym,j(i+d+p)-yr,j(i+d+p)。

(26)

文献[6]给出输入输出加权系数的在线优化算法,算法无需提供二阶导数矩阵,算法简单,计算量小,应用表明其收敛快,稳健性高。

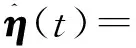
式(26)两边对η求偏导得

6 仿真研究

被控对象是关于输出非线性,输入线性的,其表达式为

设定r1(t)=(-1)＾round(t/100),r2(t)=0.6(-1)＾round(t/100),

基函数分别为阶跃函数f1,1(i)=0.3×1(t),f2,1(i)=0.75×1(t)。 斜坡函数f1,2(i)=0.2(1+i),f2,2(i)=0.15(1+i)。

加权系数初始值μ1,1(0)=0.9,μ1,2(0)=0.7,μ2,1(0)=0.7,μ2,2(0)=0.6。衰减因子γ1=0.1,γ2=0.1。

算法优化时非线性递推最小二乘法采用P(-2)=10-6I,τ1=τ2=1,μ=0.98,预测时域长度p+1=2。

采用Matlab7语言编制m文件程序进行仿真研究,仿真结果如图1和2所示。

图1 响应曲线Fig. 1 Response curve

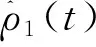
图2 加权系数的优化曲线Fig. 2 Optimization curve of weighting coefficient

7 结 论

(1)采用动态切平面逼近实用随机多变量NARMAX模型,等效为时变多变量CARMAX模型,提出递推预测模型,将非线性控制问题转化为已知时变参数的线性控制问题。

(2)提出在线优化输入输出加权系数的实用随机多变量NARMAX模型的预测函数控制,在线优化调整系数,优于试凑法确定系数的算法。

(4)因多变量双线性系统和多变量Hammerstein模型及多变量Wiener模型等非线性性模型为随机多变量NARMAX模型的特例,故均可采用文中的控制算法,避免了控制输入向量寻优的多变量非线性最优化问题。