负序零序电流对抽水蓄能电动机电磁转矩的影响

吕 品, 王凯旋, 李明军, 程鲁帅, 王浩铭, 翟悦琳

(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)

0 引 言

电动机在运行过程中经常出现故障问题,为确保系统安全稳定运行,需要重视电动机故障问题[1]。刘剑等[2]以绕组铜耗最小为优化目标及六相永磁同步电动机的转矩波动最小为约束条件,进行了转矩波动抑制。廖卫平等[3]提出一种快速解析法计算电力系统不对称故障电压跌落下感应电动机动态特性。针对三相感应电动机发生单相绕组短路故障的问题,给出场路结合的研究方法[4]。仇世龙等[5]以电网短路故障为扰动因素,分析电网短路故障下电磁转矩动态响应。戈宝军等[6]分析了发电机匝间故障前后暂态和稳态下的电磁转矩特征频谱。

电磁转矩作为研究结果的参考指标[5-6],因此,对电磁转矩的研究非常重要,可以为电动机的正常安全运行提供有价值的参考信息。Pu等[7]研究了一种考虑磁通密度谐波抑制比,提高I型磁通开关永磁电机的电磁转矩。Xin等[8]模拟了发电机在额定负载下并网时定子绕组匝间短路故障。Dajaku[9]提出了一种估算永磁电机电磁转矩、转矩密度和磁体利用率的解析方法。张炳义等[10]推导扭转角与电磁转矩削弱系数的数值表达式,建立细长转轴扭转角与电磁转矩下降的定量关系曲线。梅庆枭[11]通过得到的电感数据,计算出不同电流控制角下的电磁转矩。基于能量法分析定子绕组匝间短路故障前后电磁转矩的变化特征,仿真计算双馈异步发电机正常和不同程度匝间短路时的电磁转矩[12]。周子馨等[13]采用偏微分的方法推导出了电磁转矩的表达式。

通过上述文献可知,电动机电磁转矩的研究至关重要。因此,笔者将大型汽轮发电机电磁转矩分析方法——网络参数法[14]进行改进,充分考虑零序分量的影响,提出一种适用于抽水蓄能电动机电磁转矩的改进网络参数法。

1 改进网络参数法

1.1 基本假设

为了该方法推导结论的准确性,提出以下假设:

(1) 以抽水蓄能电动机稳定运行为前提,在中性点接地的情况下,模拟其实际稳定运行状态。

(2)当抽水蓄能电动机由正常稳定运行状态变为故障稳定运行状态时,其励磁系统和同步转速保持不变。

(3)在抽水蓄能电动机的研究中,小电流不对称度被视为低于10%的电流不对称度,大电流不对称度被视为高于10%的电流不对称度。

1.2 改进网络参数法的推导过程

抽水蓄能电动机在中性点接地及稳定运行状态下,其可被视为正序网络系统、负序网络系统和零序网络系统,如图1所示。图中,U+为正序电压;I+为正序电流;x+为正序电抗;r+为正序电阻;ra为电枢电阻;x为电枢电抗;E+为电枢绕组主磁通所产生的正序电动势;U-为负序电压;I-为负序电流;r-为负序电阻;x-为负序电抗;U0为零序电压;I0为零序电流;r0为零序电阻;x0为零序电抗。

图1 正序、负序和零序网络系统Fig. 1 Positive sequence, negative sequence and zero sequence network systems

由图1可知,电动机三相电压和电流分别为各自正序分量、负序分量和零序分量的向量和,由此,推导电磁转矩表达式。当忽略空载损耗时,计算抽水蓄能电动机的电磁功率为

pe≈uAiA+uBiB+uCiC,

(1)

式中:pe——抽水蓄能电动机的电磁功率;

uA——A相电压的瞬时值;

uB——B相电压的瞬时值;

uC——C相电压的瞬时值;

iA——A相电流的瞬时值;

iB——B相电流的瞬时值;

iC——C相电流的瞬时值。

在推导抽水蓄能电动机的电磁转矩时,正序电压和正序电流的瞬时值为

(2)

式中:ω——电角速度;

t——时间;

u+——正序电压的瞬时值;

i+——正序电流的瞬时值;

U+——正序电压U+的幅值;

I+——正序电流I+的幅值;

φ1——U+超前I+的角度。

负序电压和负序电流的瞬时值为

(3)

式中:u-——负序电压的瞬时值;

i-——负序电流的瞬时值;

δ1——U-超前U+的角度;

φ2——U-超前I-的角度。

零序电压和零序电流的瞬时值为

(4)

式中:u0——零序电压的瞬时值;

i0——零序电流的瞬时值;

φ3——U0超前I0的角度;

δ2——U0超前U+的角度。

根据式(1)～(4)整理得,适用于抽水蓄能电动机电磁功率瞬时值表达式为

pe=3[U+I+cosφ1+U+I-cos(2ωt+δ1-φ2)+

U-I+cos(2ωt+δ1-φ1)+U-I-cosφ2+

U0I0cosφ3+U0I0cos(2ωt+2δ2-φ3)]。

(5)

由式(5)可知,电磁功率可以通过正序电压、正序电流、负序电压和负序电流相互作用得到。除此之外,电磁功率可以分解为直流分量和二次谐波交流分量。其中,二次谐波交流分量揭示了正序电流和负序电压之间的相互作用,以及正序电压和负序电流之间的相互作用产生的二次谐波电磁功率。瞬时二次谐波电磁功率和瞬时基波电磁功率为

pe2=3[U+I-cos(2ωt+δ1-φ2)+

U-I+cos(2ωt+δ1-φ1)+

U0I0cos(2ωt+2δ2-φ3)],

(6)

pe0=3(U+I+cosφ1+U-I-cosφ2+U0I0cosφ3),

(7)

式中:pe2——二次谐波电磁转矩的瞬时值;

pe0——基波电磁转矩的瞬时值。

若转子转速保持同步转速,根据电磁功率和电磁转矩之间的关系,此时,瞬时二次谐波电磁转矩和瞬时基波电磁转矩分别表示为

(8)

(9)

式中:te2——二次谐波电磁转矩的瞬时值;

te0——基波电磁转矩的瞬时值;

ωs——同步角速度。

2 抽水蓄能电动机模型的建立

2.1 有限元模型的基本方程

根据具体设计参数,建立了300 MVA抽水蓄能电动机的二维有限元模型,如图2所示。

图2 二维有限元模型剖分结果Fig. 2 Results of two-dimensional finite element model

泊松方程实际上可以等价于一个变分问题,其包括边界条件,泊松方程为

(10)

式中:Ω——定子的外圆;

μ——磁导率;

Az——z轴方向上的磁矢势;

Jz——z轴方向上的电流密度。

2.2 有限元模型的验证

对300 MVA抽水蓄能电动机有限元模型进行额定稳态运行实验,额定数值和有限元模型数值对比如表1所示。其中,I为线电流,If为励磁电流,U为相电压,φ为功率因数,e为相对误差。

表1 额定数值和模型数值对比Table 1 Comparison of rated values with model values

由表1可知,额定数值和模型数值具有较好的一致性,误差范围均在5%之内,验证了有限元模型的正确性。

3 有限元模型的运行状态

通过直接在300 MVA抽水蓄能电动机模型的定子侧加三相对称电流,模拟不同额定电流的运行状态。该方法采用在抽水蓄能电动机输入端施加电流源,排除高次谐波对结果的误差影响,仅考虑基波分量对电磁转矩的影响,更能准确辨识出电磁转矩大小。根据抽水蓄能电动发电机绕组实际连接情况搭建有限元仿真的外电路,如图3所示。为了便于检查定子各相绕组电压瞬时值的情况,在有限元仿真的外电路中并联了电压表。

图3 抽水蓄能电动机有限元外电路的连接Fig. 3 Connection of finite element external circuit of pumped storage motor

三相对称正序电流数值公式为

(11)

式中:IN——定子额定电流;

ψ0——内功率因数角。

再确定负序电流不对称度以及零序电流不对称度,负序电流不对称度及零序电流不对称度分别为

(12)

(13)

三相对称负序电流数值公式为

(14)

式中:iA2——A相负序电流的瞬时值;

iB2——B相负序电流的瞬时值;

iC2——C相负序电流的瞬时值。

三相对称零序电流数值公式为

(15)

式中:iA0——A相负序电流的瞬时值;

iB0——B相负序电流的瞬时值;

iC0——C相负序电流的瞬时值。

为证明改进网络参数法的适用性广泛,分析额定电流下的稳定运行状态,以及增加3/4额定电流和额定电流两种稳定运行状态。额定电流:对有限元模型定子侧加有效值为额定电流的三相对称电流。3/4额定电流:对有限元模型定子侧加有效值为3/4额定电流的三相对称电流。调节励磁电流,使电压为有限元模型额定电流运行下的额定电压。1/2额定电流:对有限元模型定子侧加有效值为1/2额定电流的三相对称电流。调节励磁电流,使电压为有限元模型额定电流运行的额定电压。

综上所述,有限元模型分别在额定电流、3/4额定电流和1/2额定电流下稳定运行时,仅产生正序分量,得到三种稳定运行状态的电磁参数,见表2。

表2 三种运行状态的电磁参数Table 2 Electromagnetic parameters of three operating states

4 算例结果分析

在额定电流、3/4额定电流和1/2额定电流三种稳定运行状前提下,通过式(14)和 (15),在有限元模型的三相同时加对称负序电流和对称零序电流。同时,改变αi和βi的值,分别在小电流不对称度(αi<10%,βi<10%)和大电流不对称度(αi>10%,βi>10%)情况下,同时运用有限元法和改进网络参数法计算分析,观察基波电磁转矩大小和二次谐波电磁转矩幅值大小的变化趋势,得到负序、零序电流共同作用下对抽水蓄能电动机电磁转矩的影响。

4.1 基波电磁转矩

在抽水蓄能电动机有限元模型的三相同时加对称负序电流和对称零序电流,用改进网络参数法和有限元法辨识出基波电磁转矩大小。在三种稳定运行状态下,基波电磁转矩大小随小电流不对称度改变的变化趋势如图4所示。

基波电磁转矩大小随大电流不对称度改变的变化趋势,如图5所示。其中,α1为小电流不对称度;α2为大电流不对称度;T1为基波电磁转矩大小。

图5 大电流不对称度条件下基波电磁转矩Fig. 5 Fundamental electromagnetic torque under condition of large current asymmetry

通过对比图4和5可知,三种稳定运行状态,在小电流不对称度下,随着电流不对称度增大,基波电磁转矩大小基本保持不变。在大电流不对称度下,随着电流不对称度增大,基波电磁转矩大小逐渐降低。通过对比两种方法的基波电磁转矩数值大小,在小电流不对称度情况下,最大相对误差为1.25%;在大电流不对称度情况下,最大相对误差为1.55%。其相对误差均在5%之内,表明改进网络参数法可准确辨识出基波电磁转矩。

4.2 二次谐波电磁转矩

在三种稳定运行状态下,二次谐波电磁转矩幅值大小随小电流不对称度改变的变化趋势,如图6所示。二次谐波电磁转矩幅值大小随大电流不对称度改变的变化趋势,如图7所示。其中,T2为二次谐波电磁转矩幅值大小。

图6 小电流不对称度条件下二次谐波电磁转矩幅值Fig. 6 Second harmonic electromagnetic torque amplitude under condition of small current asymmetry

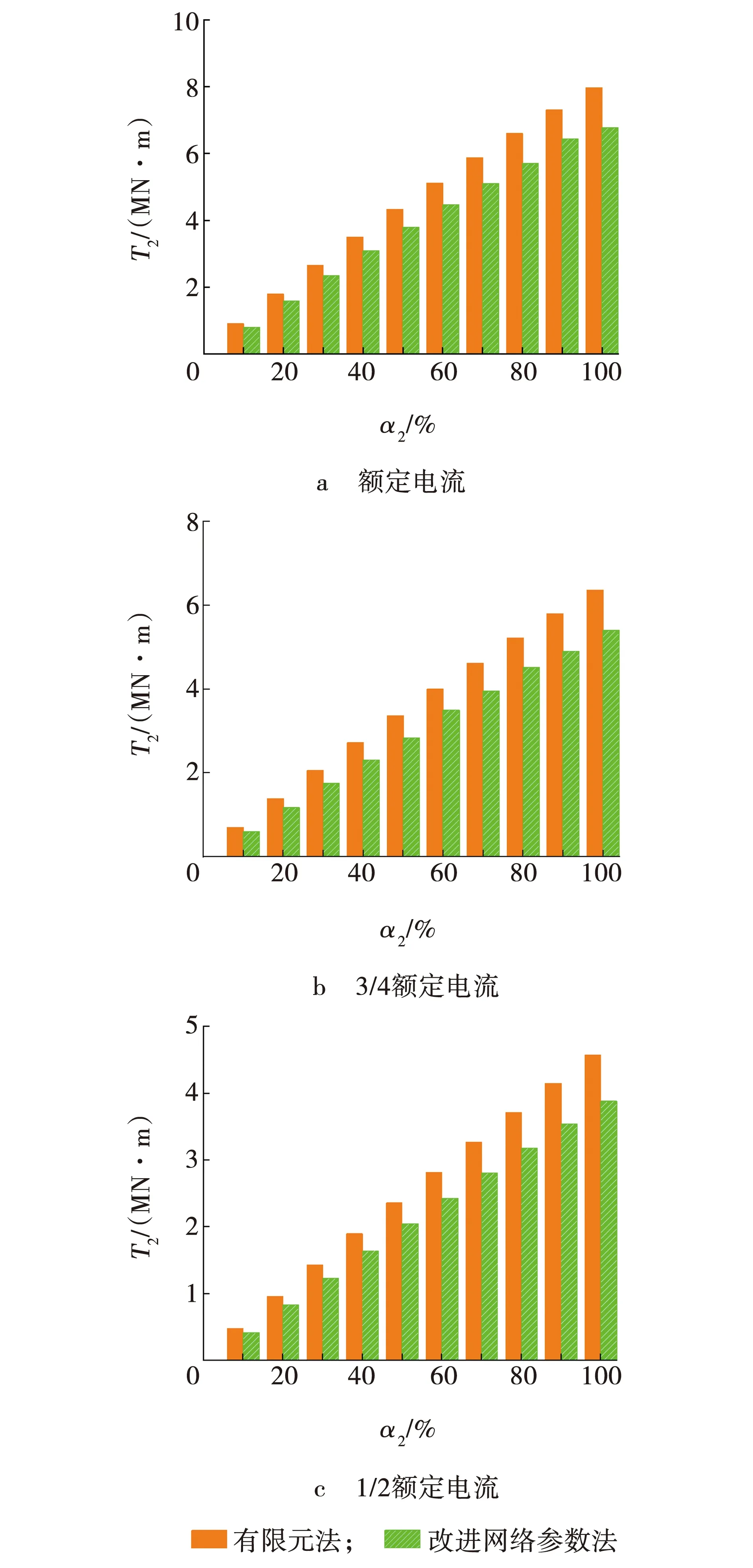
图7 大电流不对称度条件下二次谐波电磁转矩幅值Fig. 7 Second harmonic electromagnetic torque amplitude under condition of large current asymmetry

通过对比图6和7可知,三种稳定运行状态,二次谐波电磁转矩幅值大小随着电流不对称度的增加而增大,二者呈线性关系。二次谐波电磁转矩幅值大小还随着额定电流比例的增加而增大。通过对比两种方法的基波电磁转矩数值大小,在小电流不对称度情况下,最大相对误差为11.34%;在大电流不对称度情况下,最大相对误差为14.55%。

5 结 论

建立了300 MVA抽水蓄能电动机的有限元模型,电动机在额定电流、3/4额定电流和1/2额定电流三种稳定运行状态下,通过同时改变负序和零序电流不对称度,用改进网络参数法和有限元法分别计算相应运行状态下基波电磁转矩大小和二次谐波电磁转矩幅值大小,验证改进网络参数法的准确性并分析电磁转矩随电流不对称度大小改变的变化趋势,得到以下结论:

(1)改进网络参数法可辨识出额定电流比例不同,以及不同电流不对称度的情况下的二次谐波电磁转矩幅值和基波电磁转矩大小。

(2)随着负序和零序电流的同时增加,在小电流不对称度范围内,对基波电磁转矩大小的影响很小,其数值基本保持不变;在大电流不对称度范围内,基波电磁转矩大小随电流不对称度的增加而减小。

(3)二次谐波电磁转矩幅值大小随着电流不对称度的增加而线性增加。