非线性反应扩散方程的高精度有限差分方法
2023-06-29刘圣恩葛永斌祁应楠
刘圣恩,葛永斌,祁应楠
(1.宁夏大学数学统计学院,宁夏 银川 750021;2.宁夏师范学院数学与计算机科学学院,宁夏 固原 756000)
1.引言
反应扩散方程是一类描述物理量随时间扩散和衰减的抛物型微分方程.自然环境、生物竞争及工程设备中的诸多物理现象,如种群中基因的扩散、半导体材料中的杂质或者河流中污染物浓度的变化、液体的渗透等都可用反应扩散方程进行描述[1].
近年来,有众多科研工作者致力于有限差分法的高精度差分格式的研究,并且已有的研究结果表明,提高数值方法的精度对于提高问题的求解能力是一种非常有效的途径.LI等人[2]针对一维非线性反应扩散方程,提出了一种预测-校正格式,通过用隐式-显式(IMEX)方法来避免迭代,该格式时间具有二阶精度,空间具有四阶精度.葛永斌等人[3]针对一维扩散问题构造了一种时间二阶精度,空间四阶精度的隐式差分格式,且用Fourier分析方法证明了格式是无条件稳定的.田振夫等人[4]利用三次样条四阶差分方法,提出了扩散方程的两种无条件稳定的差分格式,该格式时间具有二阶精度,空间具有四阶精度.黄文姣等人[8]针对一维非线性反应扩散方程,采用四阶向后差分处理时间导数,空间项采用四阶紧致算子进行离散,得到一种时间和空间均为四阶精度的格式.WANG等人[6]针对一维非线性反应扩散方程,提出了一种时间具有二阶精度,空间具有四阶精度的单调紧致隐式有限差分格式.张林等人[7]针对二维非线性反应扩散方程,时间项和空间项分别采用四阶向后差分和四阶紧致差分方法进行离散,提出了一种高精度的全隐格式,并采用多重网格算法加速求解全隐格式所形成的代数方程组.WU等人[5]针对二维非线性反应扩散问题构造了一种两层线性化的交替方向隐格式,并给出了无穷范数和L2范数的误差估计,该格式时间具有二阶精度,空间具有四阶精度.
综上所述,针对反应扩散方程,上述各类格式的空间精度均不超过四阶,空间具有六阶精度的格式尚未发现研究报道.从已有的文献来看,实现空间六阶精度有几类常见的方法.SUN等人[9]针对抛物型方程,空间采用六阶组合紧致差分格式(CCD)进行离散,时间采用Crank-Nicolson(C-N)方法进行离散.该格式的空间离散方法,需要分别构造求解未知函数u及u的一阶和二阶空间导数的六阶差分格式,然后通过迭代方法求解u,进而达到六阶精度求解的目的.该方法的实现比较复杂,因此应用相对较少.Sari等人[10]针对抛物型方程,空间采用导数型六阶格式进行离散,时间方向采用TVD-RK3方法进行离散.该格式在计算上简单高效,但稳定性较差,因此制约了该格式的推广和应用.针对以上六阶方法的不足,本文针对二阶导数,提出一种推导简洁且有效的五点六阶差分公式,并运用该差分公式来求解一维非线性反应扩散方程.
2.高精度有限差分格式
考虑如下一维非线性反应扩散方程的初边值问题:
初始条件为:
边界条件为:
其中u(x,t)为待求未知量,υ >0为扩散项系数,f(u)为非线性源项,且φ(x),g(t),l(t)均为已知函数.为简化分析,设u(x,t)具有充分的光滑性.
首先对计算区域进行等距网格剖分,分割[a,b]×(0,T]为N ×M(N,M ∈Z+)网格,设时间步长为τ=,空间步长为h=,用表示网格点(xi,tn)的数值解,其中xi=a+ih,i=0,1,···,N,tn=τn,n=0,1,···,M.网格节点图如下图所示:
分别将点ui+1,ui−1,ui+2,ui−2在点ui处进行Taylor展开:
将上面两个式子分别求和得到如下的式子:
将(2.7)-(2.6)×16,(2.7)-(2.6)×64分别得到
定义如下五点中心差分算子
将式(2.8)和(2.9)分别写成如下形式
将(2.12)式略去高阶误差项,代入(2.13)式可得
从而得到全新的二阶导数的五点六阶差分公式
对方程(2.1)空间内部点用式(2.15)进行离散,得
整理得到:
将算子(2.10)和(2.11)代入式(2.17)整理得到空间离散格式
考虑式(2.18)在(n −1/2)时刻的值:
对式(2.19)时间导数项采用C-N方法进行离散,空间采用加权平均,得到:
上式舍去截断误差项,两边同乘以τ,并令r=τ/h2,整理得到:
式(2.21)就是定解问题(2.1)-(2.3)的高精度差分格式,该格式的截断误差为O(τ2+h6),即时间具有二阶精度,空间具有六阶精度.由于采用五点模板来构建格式,临近边界点的计算需要单独处理.我们利用计算域以外两个虚拟点的方法,来实现两个临近边界点的计算.虚拟点的处理公式如下:
式(2.21)空间精度具有六阶,而时间精度仅具有二阶,为了让格式在求解中体现出更好的计算性能,构造时间和空间精度更为接近的格式是十分必要的.为此,本文采用如下四阶Richardson外推公式[11]
通过式(2.21)(2.23)就得到求解方程(2.1)-(2.3)的高精度差分格式,该格式时间具有四阶精度,空间具有六阶精度.在算例1(具有精确解)计算中,为了体现格式更好的计算性能,对格式应用外推算法,在算例2(爆破问题)和算例3(quenching问题)计算时,由于选取的时间步长充分小,因此不必要应用外推算法,仅应用式(2.21)进行求解.
由上述分析和推导过程,可以建立求解算法描述如下:
3.稳定性分析
下面采用von Neumann方法对线性化格式进行稳定性分析,为此假设虚拟边界条件精确满足,且右端项f无误差存在.用=(xi,tn)表示计算所产生的误差.将代入式(2.21)中,得到如下误差等式:
由于A,B均为非负实数,因此|G|≤1,从而得出本文格式是无条件稳定的.
4.数值算例
算例1考虑如下具有精确解的问题:
算例1是一个非线性问题,方程源项是含有未知函数u(x,t)的非线性函数.表1给出了当T=1,τ=0.001时的‖eh‖∞范数误差和空间收敛阶.从表1可以看出,本文格式在空间上可以达到六阶精度,而且比C-N格式和文[8]中格式的计算结果更加精确.表2给出了当T=1,h=1/128时的‖eh‖∞范数误差和时间收敛阶.从表2中可以看出,本文格式在时间上具有四阶精度,且比C-N格式和文[8]中格式的计算结果更加精确.
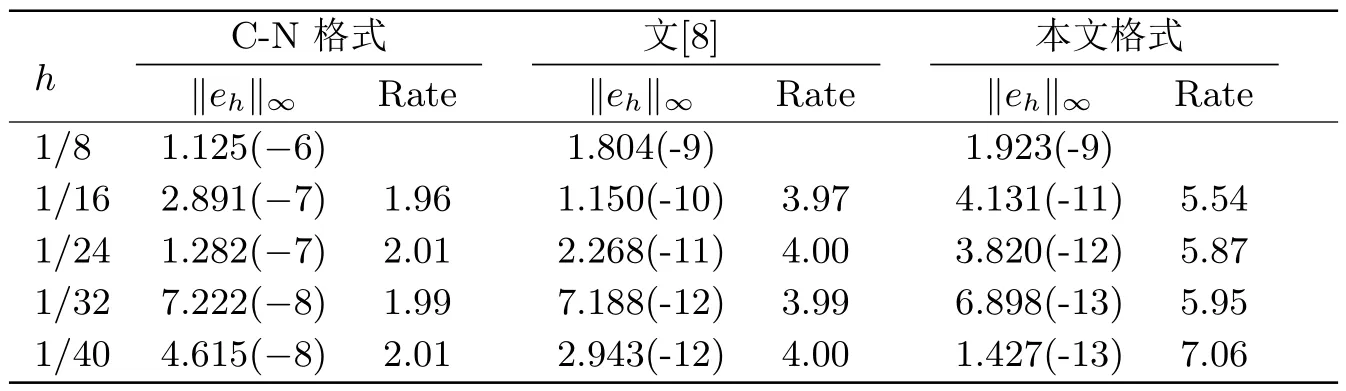
表1 当T=1, τ=0.001时,算例1的‖eh‖∞范数误差和空间收敛阶

表2 当T=1, h=1/128时,算例1的‖eh‖∞范数误差和时间收敛阶
算例2考虑如下解的爆破问题:
从表3计算结果可以看出,当α取不同值时,古典隐格式(BTCS)爆破时间的收敛阶均为二阶.本文格式当α=2时,爆破时间的收敛阶为二阶,但当α=5/2,3时,本文格式比BTCS格式具有更高的收敛阶.充分说明了本文格式在爆破问题的数值模拟中相较于低阶格式的优势.
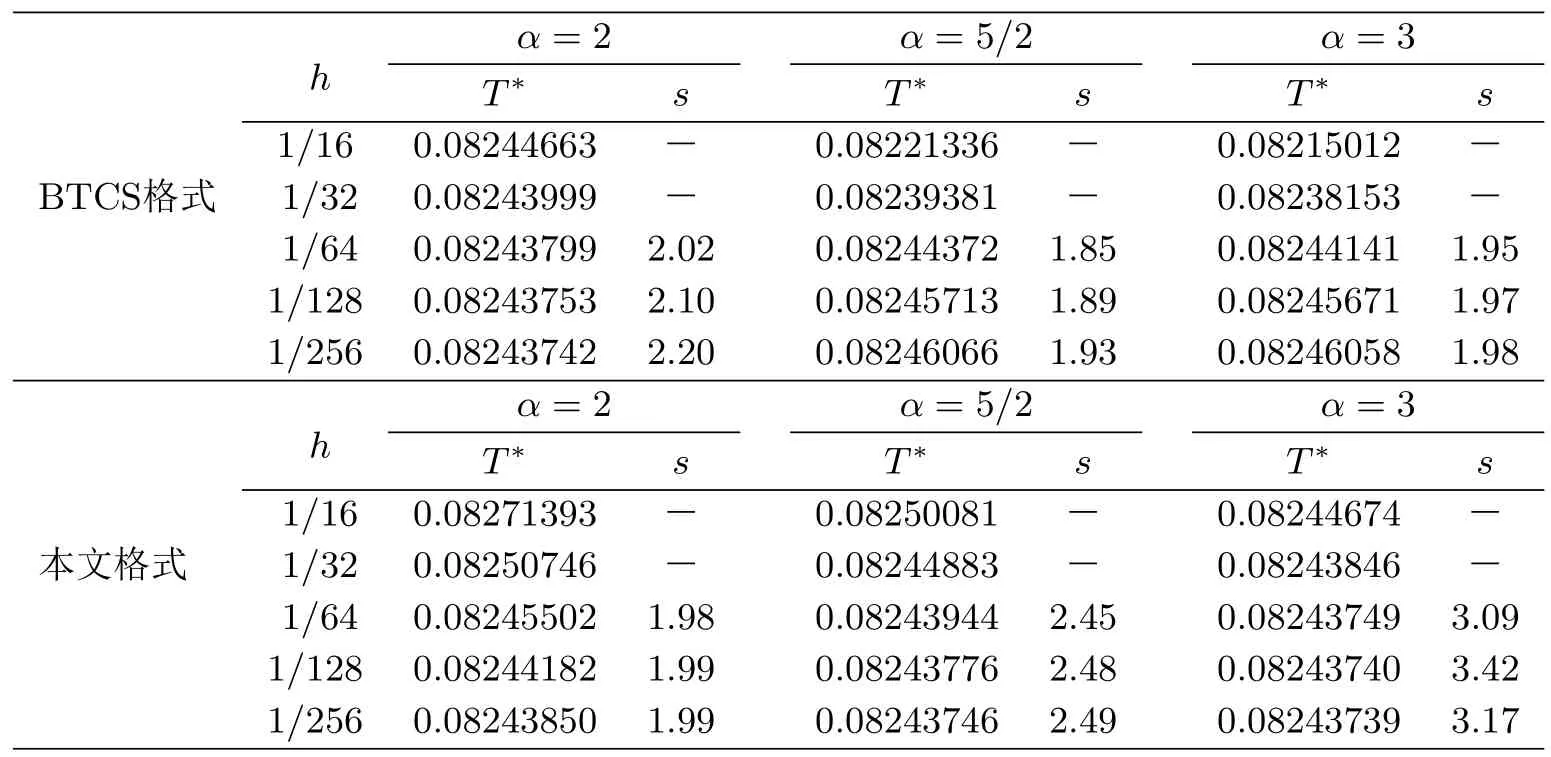
表3 当α=2,5/2,3时,BTCS格式和本文格式的爆破时间及收敛阶
图1为本文格式当空间网格划分取N=64,α=1时对爆破现象的数值模拟图,其中图(a)为从t=0时刻一直到爆破发生时数值解u随时间和空间的变化;图(b)为当爆破发生之时,即当T∗=0.08357703时,在整个空间区域上u的数值结果图,图中很好展现出了数值解的爆破现象.

图1 当N=64,α=1时,(a)u 随空间和时间的变化图;(b)在发生爆破现象的时刻(T∗)u的数值
算例3考虑如下的quenching问题:
该问题的显著特征是,随着时间的推移,u →1−而ut →+∞,此类问题被定义为quenching问题[14].当τ=5×10−5,h=l×10−2时,采用本文格式计算得到的quenching时间Tl与文[15]中的quenching时间,及文[16]中的quenching时间的对比数据如表4所示.可以看出,分别取不同的计算区域l,本文格式的quenching时间Tl与,结果相近.
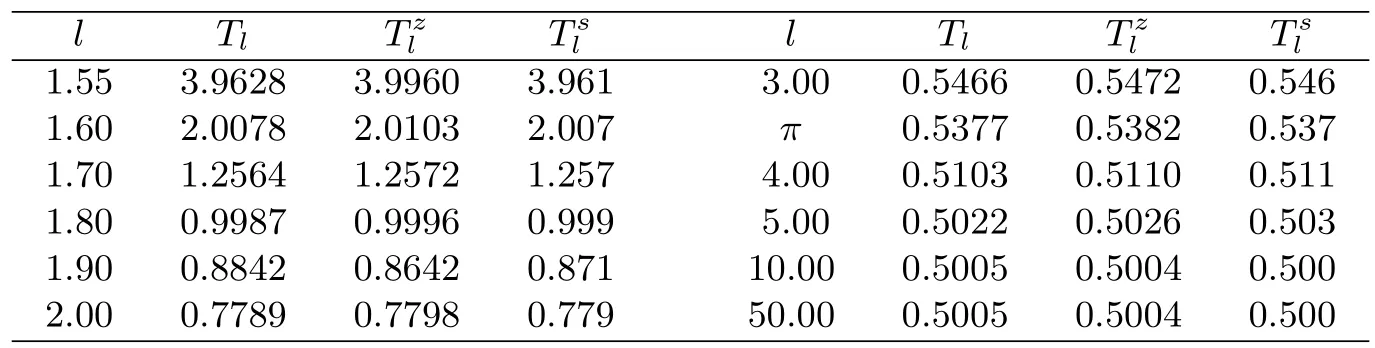
表4 当τ=5×10−5, h=l×10−2时,quenching 的发生时刻
当τ=5×10−5,h=l×10−2,l=2时,图2给出了quenching发生时刻(=0.7789)的u和ut在x ∈[0,l]的值;图3给出了在quenching现象发生之前u和ut的最大数值解随时间的变化图;图4给出了u和ut在quenching发生之前,最后80个时间步的三维视图.可以看出,u在x=1处无限接近于1,而ut在x=1处逐渐增大直至=0.7789时刻发生爆破.
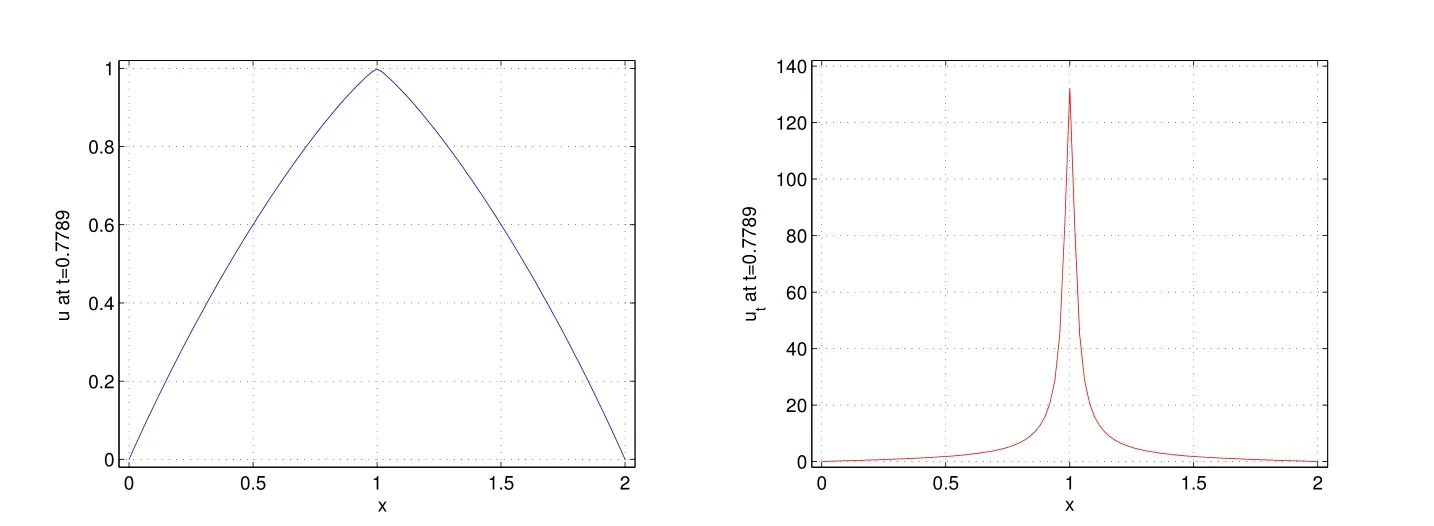
图2 u, ut 在quenching时刻(=0.7789)的值
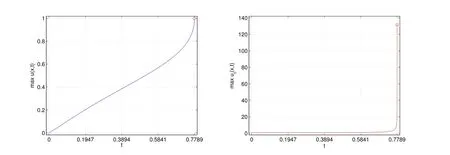
图3 的值随时间t的变化图

图4 u, ut在quenching发生前80个时间步的三维视图
5.结论
针对空间二阶导数,提出了一种五点六阶差分公式.基于该差分公式建立了求解一维非线性反应扩散方程初边值问题的一种高精度有限差分格式,并采用Richardson外推方法将时间精度提高到四阶.在每一时间层上形成的线性方程组采用五对角追赶法进行求解,对非线性源项进行迭代计算.最后,通过数值实验验证了本文格式在时间和空间上分别能达到四阶和六阶精度,计算结果相比于相关文献中的结果更加精确.在针对爆破的数值模拟中,本文方法具有较高的爆破时间收敛阶;而针对quenching问题的模拟中,quenching时间与相关文献中时间基本一致,因此也充分说明了本文格式可以很好地模拟爆破和quenching现象.
本文方法可推广到求解高维及更复杂的偏微分方程.我们正在进行的研究工作和相应的结果将在之后报道.
