求解非线性方程组的修正Fletcher-Reeves共轭梯度法

黎勇,罗丹,王松华

(百色学院数学与统计学院,广西 百色 533000)

1.引言

考虑如下非线性方程组问题:

式中g: Rn →Rn连续可微.非线性方程组问题在压缩感知[1],以及化学平衡、经济平衡、电力系统领域等实际工程问题上有着较强的应用背景[2],一直得到了广泛的研究,出现了牛顿算法、拟牛顿算法、高斯牛顿算法等收敛性理论较好的算法.然后这些算法普遍因为存储量大、算法较为复杂等因素限制,不适合求解大规模非线性方程组问题.共轭梯度算法存储量需求小、算法结构简单,是求解大规模无约束优化问题最有效的算法之一,近年来被推广到大规模非线性方程组问题,并成为最优化领域研究的一个热点[3−7].令f(x)=是欧几里得范数,则问题(1.1)与式(1.2)等价,非线性方程组问题(1.1)转化为如下无约束优化问题:

求解无约束优化问题(1.2)的共轭梯度法迭代公式如下:

式中dk是搜索方向,αk是搜索步长,βk+1是控制参数,不同的控制参数βk+1对应不同的共轭梯度法.FR算法[8]、PRP算法[9]和HS算法[10]等经典共轭梯度法已广泛被人们所熟知,其中FR方法的控制参数公式如下:

FR算法收敛性质较好,但因为可能会连续产生小步长而导致数值表现一般[8].PRP算法和HS算法数值表现较好的一个原因之一,是其搜索方向dk能够自动靠近负梯度方向[9−10],克服了FR算法的不足.因此,从PRP算法或HS算法中寻找更有效的FR方法的修正技术,理论上是有可能的.

在非精确线搜索分析中,设计具有不依赖任何线搜索自动满足充分下降条件[11−13]和信赖域性质[14−15]的搜索方向,所构建算法在更温和的条件下的全局收敛理论性质更好,数值结果表现更优.所谓的充分下降条件是:=−c‖gk‖2,∀k ∈N,c <0,信赖域性质是‖dk‖≤−c0‖gk‖,∀k ∈N,c0>0.近来,一类具有自动满足充分下降条件的共轭梯度算法,有效求解了非线性方程组问题[16−18].其中,文[16]提出了一类新型的无导数PRP共轭梯度算法,其搜索方向公式为:

式中:δk=gk+1−gk,γ >0.该算法保持了文[16]自动满足充分下降条件的性质,还克服了文[16]不具有的信赖域性质的不足,其搜索方向公式更为简便,算法效果更好.文[18]也有类似的思想,所设计的算法收敛性更快,数值结果更好.文[17-18]不仅能有效求解问题(1.1),特别在大规模优化问题上,效率更好.

基于以上讨论,本文在经典FR算法的基础提出一种新的搜索方向,结合超平面投影技术和文[18]的经典线搜索,设计一类针对非线性方程组的修正FR算法.研究表明该算法不仅自动满足充分下降条件,而且搜索方向具有信赖域性质,在一定条件下所提出的方法全局收敛.初步的数值实验也表明修正FR算法在求解非线性方程组方面更加高效.

2.MFR算法(Modified Fletcher-Reeves Method)

本节结合文献[17,18]的技术,在经典FR方法的基础上,设计一个新的搜索方向如下:

式中: 常数µ1>0,µ2>0.显然,在精确线搜索条件下,当目标函数为严格凸二次函数时,(2.1)式退化为经典FR方法.

为便于表述,本文将修正FR算法简称为MFR算法,其步骤如下:

算法1(MFR算法)

步0 给定初始点x0∈Rn.ε ∈(0,1),µ1>0,µ2>0,σ >0.令k:=0.

步1 若‖g(xk)‖<ε则停止;否则转步2.

步2 利用式(2.1)计算搜索方向dk.

步3 利用文[18]计算步长αk:

其中αk=max{s,λs,λ2s,···},σ >0,s>0,λ ∈(0,1).

步4 令迭代公式为zk=xk+αkdk.

步5 若‖g(zk)‖≤ε则停止,并令xk+1=zk;否则下一个迭代点xk+1取xk在超平面Hk=上的投影[19]:

步6 令k:=k+1,转步1.

3.全局收敛性

假设A非线性方程组问题(1.1)的解集是非空集合,水平集Ω={x∈Rn:f(x)≤f(x1)}有界.

假设B映射g在Rn →Rn上Lipschitz连续,即存在L>0,使得

由以上假设容易推出存在一个常数ξ >0,使得

引理3.1若搜索方向dk满足式(2.1),则下列性质成立:

证当k=0时,式(3.2)、式(3.3)显然成立.当k ≥1时,由式(2.1)有

即式(3.2)成立.因此由Cauchy-Schwartz不等式得

故式(3.3)左边不等式成立.

另一方面,式(2.1)两边同取范数,并再次利用Cauchy-Schwartz不等式得

综上所述,(3.3)式得证.证毕.

引理3.2[19]令假设A、B成立,序列{xk}由MFR算法产生,若x∗是非线性方程组(1.3)的解,即g(x∗)=0,则

成立.

以上引理及其证明详见文[19].

引理3.3若假设A、B成立,则MFR算法经有限次回溯后必产生迭代xk+1=xk+αkdk,即MFR算法有意义.

证反证法.假设MFR算法不停止或者‖gk‖→0不成立,则存在常数η >0,使得

下面证明: 线搜索(2.2)能保证获得一个正的步长,使之在有限步内终止,即证明满足线搜索(2.2)的步长αk有下界.利用反证法,假设存在k′使(2.2)不成立,则对∀m ∈N∪{0},令,有

由假设B和式(3.2)有

而根据式(3.1)、式(3.3),有

由式(3.3)、式(3.5)、式(3.6)得

根据以上三个引理,下面证明MFR算法在一般条件下全局收敛.

定理3.1设序列{αk,dk,xk+1,gk+1}由MFR算法产生,假设A,B成立,则

证反证法.假设式(3.7)不成立,则式(3.4)成立,故由式(3.3)有

因为由引理3.2中序列{xk}的有界性知道,必存在一个聚点和无限指数集N1,使

同理由式(3.1)、式(3.3)得到

也说明序列{dk}有界,因此也必存在一个聚点和无限指数集N2⊂N1,使

另外由引理3.2和引理3.3容易知道

因此

因为根据式(2.2)不难得到

当k →∞时,对所有k ∈N2,式(3.10)两边同取极限得

而当k →∞时,对所有k ∈N2,式(3.2)两边同取极限得

4.数值试验

为了验证MFR算法求解非线性方程组的有效性,下面将对表1中的测试问题进行数值实验,所选测试问题来自文[20-21].每个测试函数取[500,1000,3000,5000]等4种维数情形,并从迭代次数(NI)、函数值计算次数(NG)、算法终止时函数的范数值(GN)、实验所需时间(CPU time)等几方面将MFR算法的实验结果与传统FR方法的实验结果进行比较.

数值试验是在Win 7.Pentium Dual E5800 3.20GHz,内存2.0G的PC机上进行的,测试代码利用Matlab R2010b编写,各参数取值如下:µ1=0.99,µ2=0.01,ε=10−5,终止条件为‖g(x)‖≤10−5或者NI≥1000.表4.1列出了数值实验结果,表4.2列出6个测试问题的名称和初始点.

表4.1 数值结果

表4.2 测试问题

为了更加直观地比较两种算法对以上测试问题的数值表现,根据Dolan和Mo´re在文[22]中提出的评价方法,利用Matlab编写程序得到以下三个数值实验结果的比较图像:

图4.1 MFR算法与FR算法的NI性能比较

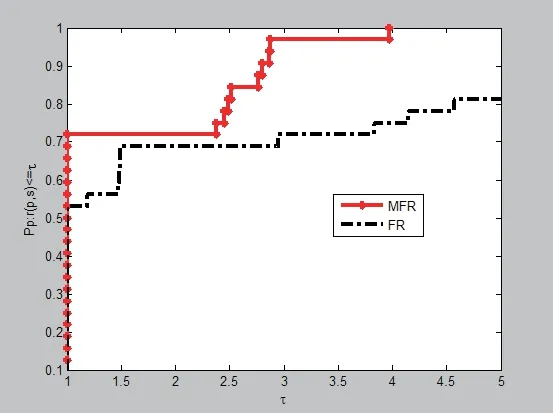
图4.2 MFR算法与FR算法的NG性能比较

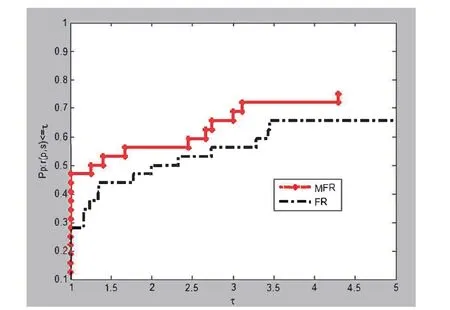
图4.3 MFR算法与FR算法的CPU time性能比较

从图4.1-4.3,容易直观看出,无论是迭代次数、函数值计算次数,还是实验所需时间,代表MFR算法的曲线基本上都在代表传统FR算法的曲线上方,这表明MFR算法求解问题的成功概率更大,而且鲁棒性更强,稳定性更高.针对这本次的6个测试问题,两类算法是有效的,MFR算法总体效能优于FR方法.

5.结语

本文提出一种求解非线性方程组问题的MFR算法,该算法具有自动满足充分下降条件和信赖域性质的特点,具有很好的收敛性质;数值结果表明,MFR算法比经典FR算法更高效.未来我们将加大数值实验测试问题的个数和维数,如10个以上测试问题,每个问题的维数设定到5万维以上,进一步验证MFR算法的稳健性和有效性.同时,尝试将MFR算法推广到压缩感知等实际工程问题中,推广MFR算法的应用价值.