四耦合非线性薛定谔方程的矢量孤子解及叠加解

胡雪原,郭睿

(太原理工大学数学学院,山西 晋中 030600)

1.引言

众所周知,非线性发展方程在非线性科学的各个领域,如水波、非线性光学和流体力学中都发挥着重要作用.其中,非线性薛定谔方程更是几十年来科研工作者的重点研究对象.如在物理学的光纤通信系统中,非线性薛定谔方程可以用来描述光脉冲的传播.但是由于自然现象在现实世界和某些实验环境中下更为复杂,耦合方程的研究比单分量方程受到了更多研究人员的关注.

时至今日,非线性偏微分方程的求解一直都是非线性科学的重要内容之一.近来,对于非线性偏微分方程提出多种求解方法,如广田双线性方法、达布变换方法、反散射方法等.广田双线性方法[1−3]是通过一个适当的变换,将非线性偏微分方程转化为双线性形式,再通过截断小参数多项式得到精确解.达布变换方法[4−6]是利用不同的种子解,然后进行迭代得到新解.这两种方法,在高维非线性偏微分方程的求解与相关问题的研究中被广泛应用.文[7-8]利用发展的广田双线性方法分别得到了二耦合和三耦合非线性薛定谔方程的矢量孤子解,并分析了这些解的动态行为.文[9-10]利用达布变换方法分别得到了二耦合和三耦合非线性薛定谔方程的怪波解及怪波与孤子、呼吸子相互作用的叠加解.

本文基于文[7-10],研究了以下的四耦合非线性薛定谔方程的矢量孤子解及一阶怪波及叠加解[11]:

首先,通过发展的广田双线性方法得到方程(1.1)的单、双孤子解,然后通过选取不同参数,得到三类矢量孤子解并分析这些解的性质.最后,通过一阶的达布变换得到一阶怪波及怪波与孤子、呼吸子的叠加解.

2.矢量单、双孤子解

为了得到方程(1.1)的孤子解,对方程(1.1)中的变量ϱα做有理变换.令,α=1,2,3,4,得到方程(1.1)的双线性形式：

将Gα和F展开成小参数ε的幂级数:

单孤子解为了得到单孤子解,将方程(2.2)截断为以下形式:

双孤子解为了得到双孤子解,将方程(2.2)截断为以下形式:

因此,得到方程(1.1)的双孤子解为:

3.矢量孤子解的性质

情形1选择参数γ0=0,其他参数在满足限制条件的情况下任意取值.我们可以得到亮孤子.方程(2.5)可以如下表达:

其中θ1R=k1Rx−2k1Rk1It+φ1R,θ1I=.根据方程(2.5)和方程(2.8)的特点,下面我们只给出ϱ1的图像.由方程(3.1)可知,亮孤子的振幅和速度为:

由图3.1可以观察到,亮单孤子在传播过程中保持振幅、速度不变.而为了研究双孤子解的性质,我们将对方程(2.8)进行渐近分析.

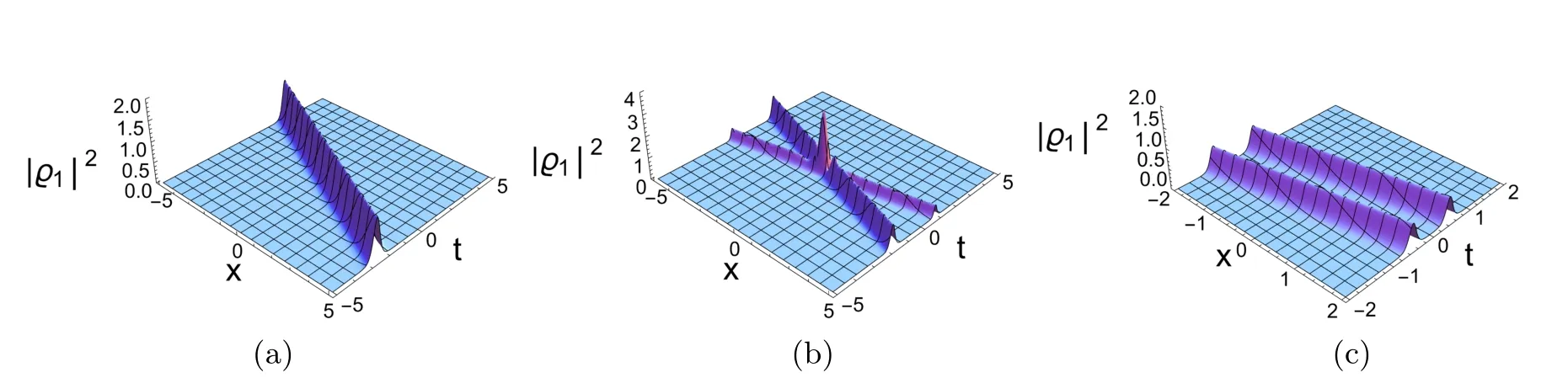
图3.1 a=b=c=d=m=u=1, n=v=−1, γ0=0, k0=1.2,(a) k1=2 −i,φ1=1;(b) k1=2.1 −1.4i,k2=1.5+2.8i,φ1=1,φ2=1;(c) k1=1.5+2.8i,k2=1.6+2.8i,φ1=1,φ2=1

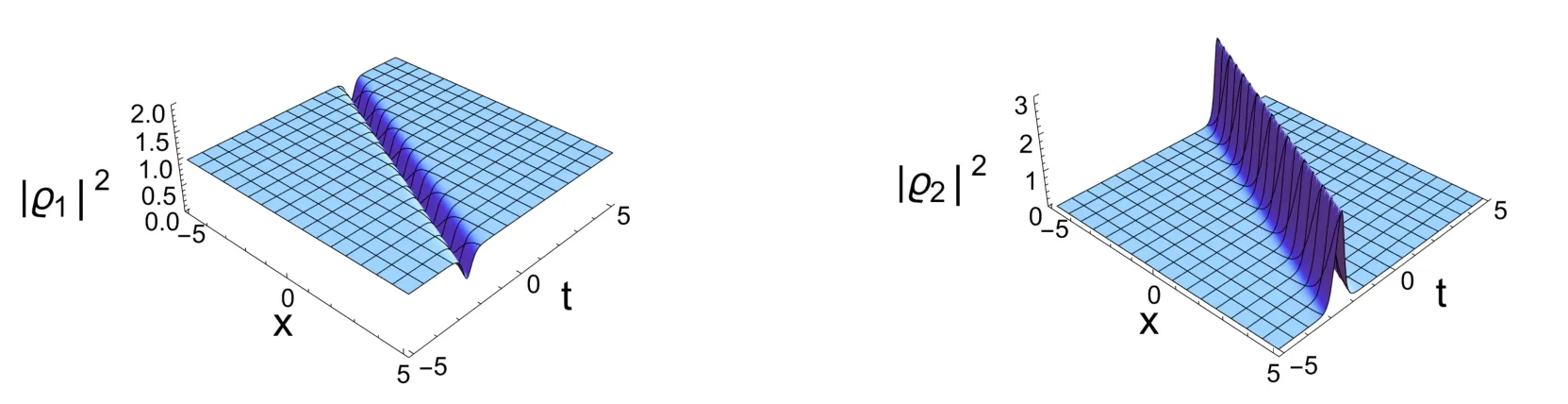
图3.2 a=n=1,b=d=m=u=0,c=v=−1,γ0=1,k0=1.2,φ1=1,k1=2 −i

碰撞前(t →−∞):

碰撞后(t →+∞):

通过观察图3.1以及比较碰撞前后孤子的振幅、速度、相位:

情形2选择参数γ0≠0,b=d=m=u=0.我们可以得到亮暗孤子.方程(2.5)可以如下表达:

根据方程(2.5)和方程(2.8)的特点,下面我们只给出ϱ1和ϱ2的图像.由方程(3.6)可知,解ϱ2和ϱ4为亮孤子,解ϱ1和ϱ3为暗孤子.亮暗孤子的振幅和速度为:

同样地,为了分析亮暗双孤子解的性质,我们对方程(2.8)进行渐近分析.

碰撞前(t →−∞):

碰撞后(t →+∞):

通过观察图3.3以及比较碰撞前后的振幅、速度、相移:

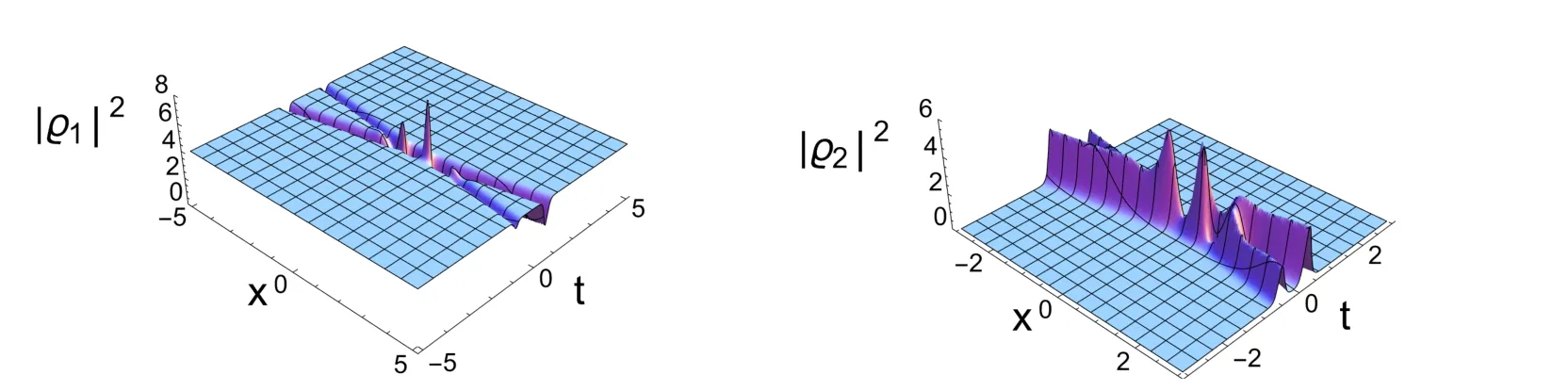
图3.3 a=n=1,b=d=m=u=0,c=v=−1,γ0=2,k0=1.2,φ1=1,φ2=1,k1=1.5+2.8i,k2=1.6 −2.8i

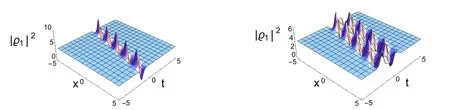
图3.4 a=b=c=d=m=v=1, n=u=−1, γ0=2,k0=1.2,(a) k1=1.5 −2i,φ1=1;(b) k1=1 −2i,k2=0.8 −2i,φ1=3,φ2=1

同样地,我们发现亮暗双孤子解之间的碰撞也是弹性的.

情形3令所有参数都不为0.方程(2.5)可以如下表达:

根据方程(2.5)和(2.8)的特点,我们只给出ϱ1的图像.在这样的参数下,我们可以得到一种具有呼吸行为的新解.

4.一阶怪波及叠加解

方程(1.1)的Lax对如下所示:

其中Ψ=(ϕ1,ϕ2,ϕ3,ϕ4,ϕ5)T,ϱα(α=1,2,3,4)是势函数,ζ是谱参数.经验证,上述Lax对满足相容性条件Ut −Vx+[U,V]=0.

基于AKNS谱问题,可以构建方程(1.1)的达布变换[4]:

其中ϱα=ϱα[0],Ψ1=Ψ(x,t,ζ1)(c1,c2,···,cN)T,ζ1是复数,c1,c2,···,cN是常数.下面我们给出证明.

如果Tx+TU=T,且与U有相同的形式,那么我们有

类似地,如果Tt+TV=T,且与V有相同的形式,那么我们有

事实上,我们容易验证T保持与U有相同的形式.下面我们验证T保持与V有相同的形式.

即下面等式成立:

当ζ/=ζ1,时,达布变换T是一个非退化的矩阵.另一方面,我们可以计算上面两式左端关于ζ矩阵函数在ζ=ζ1,是留数为零,且在无穷远处趋于0.那么,由刘维尔定理可得上面两式在整个复平面恒成立.进而由相容性条件(4.4)(4.5)可以推出

直接计算,我们可以推出

证毕.

通过上面的定理,我们得到势函数之间的变换:

上式的参数如下:

情形1δ1=δ2=δ3=0,χ1,χ2,χ3,χ4可以任意取值.我们可以得到一阶怪波解.

图4.1中展示的图像和单分量非线性薛定谔方程的一阶怪波相同.

图4.1 δ1=δ2=δ3=0,χ1=χ2=χ3=χ4=1

情形2δ1,δ2,δ3≠0,χ1,χ2≠0,χ3,χ4=0.我们可以得到一阶怪波与孤子的叠加解.

图4.2中的一阶怪波因为出现在零振幅背景波峰处,因此它们的振幅非常小.

情形3δ1,δ2,δ3,χ1,χ2,χ3,χ4≠0.我们可以得到一阶怪波与呼吸子的叠加解.

通过对比图4.3和图4.4,可以发现改变δ1,δ2,δ3的值,呼吸子和怪波发生了分离.并且当δ1,δ2,δ3的值由时,解ϱ4的波形发生改变.

图4.3

图4.4