悬链线拱桥主拱圈变截面高度的数值计算方法

由变截面拱圈的截面变化方式引入，依据微积分弧微分公式计算曲线长度的原理，推导出悬链线拱轴线长度的计算公式无法用初等函数表示，由此引入数值积分的方法求解轴线长度，进而深入了解自适应辛普森积分法，采用Excel中的Visual Basic语言自编程序验证理论充分可行。

悬链线； 变截面； 合理拱轴线； 自适应辛普森积分； Visual Basic

U448.22+5 A

［定稿日期］2022-03-23

［作者简介］白高（1995—），男，本科，助理工程师，从事市政、公路桥梁设计工作。

拱桥具有独特的山区地形适应能力、强大的跨越能力以及可靠的使用性能，已经成为我国公路、铁路广泛使用的一种桥型。拱桥主拱圈作为主要受力构件，起着传递和承受荷载的重要作用，拱桥主拱圈线形又对主拱圈的受力合理性、建设经济性起着至关重要的作用，拱轴线常用类型有圆弧线、抛物线、悬链线。圆弧线适用于承受径向均布荷载的结构，圆弧线拱在水工结构中多见，在桥梁结构中为施工方便，圆弧线多用于跨径20 m以下的小跨径拱桥；抛物线形拱轴线适用于拱圈承受均布荷载，理论上抛物线适用空腹式拱；悬链线形拱轴线适合承受拱顶至拱脚连续变化的荷载，是实腹式拱桥的合理拱轴线。虽然空腹式拱桥采用悬链线形拱轴线在恒载作用下压力线与拱轴线存在偏离，但计算表明该偏离通常对拱圈控制截面受力是有利的，并且，仅需使拱轴线与恒载压力线在拱顶、1/4跨径点和拱脚五点重合即可实现拱内弯矩最小化，因此，悬链线是目前大、中跨径拱桥采用最普遍的拱轴线形［1］。

对大跨径拱桥，拱圈截面惯性矩采用拱顶至拱脚变化的方式，拱圈惯性矩变化通常是为了适应拱内内力变化，惯性矩的变化通常表现为拱圈高度的变化（图1），拱圈高度的合理变化有利于充分发挥拱桥的每个截面的材料强度［2］。对于无铰拱，通常根据李特公式（Ritter 公式［1］）来改变截面惯性矩，在设计工作中，直接应用李特公式逐个计算截面高度不便操作，原因是工程中拱圈截面形状复杂、不同的材料在截面中分布的规律性与截面高度之间的关系无法通过简单的数学模型描述（板拱除外），因此对复杂截面李特公式不能直接快速得到截面高度；为简单实用起见，设计大跨径拱桥时工程师常采用沿拱轴线长度（弧线）方向，拱圈截面高度采用抛物线渐变的方式，即拱圈截面高度是拱轴线弧长的抛物线函数，这就是要解决的问题：如何计算变截面中各变化点的截面高度，得到拱圈设计坐标。

将自适应辛普森算法的原理通过Excel中VBA语言编制成程序，将程序计算结果与实际工程中的设计值对比验证，论证方法的可行性和正确性。

1 理论计算原理

一元函数积分计算原理是牛顿-莱布尼兹原理，即找到被积函数的原函数，将积分上下限代入原函数作差，这是微积分的基本原理。牛顿法计算定积分的前提是被积函数的原函数能用初等函数表示，下面讨论悬链线方程（图2）。

由《桥梁工程》教材［1］，悬链线的方程为式（1）。

y=fm-1（coshkξ-1）（1）

其中：

k=cosh-1m=ln（m+m2+1）（2）

其中：

ξ=xl1=xl/2=2xl（3）

由《高等数学》［3］教材得悬链线的弧微分为：

ds=1+y′2dx（4）

将式（1）、式（3）代入式（4），借助数学专业程序Wolfram Mathematica 12.1计算得到式（4），结果为式（5）。

ds=1+4f2k2Sin（2kx/l）2l2（m-1）2dx（5）

于是弧长计算的原函数用Wolfram Mathematica 12.1程序计算为：

∫1+4f2k2Sin2kxl2l2（m-1）2dx=-lEllipticE2ikxl，4f2k2l2（m-1）22k+C（6）

式（6）中i为虚数符号，EllipticEφ，m为第二类椭圆积分，第二類椭圆积分是无法通过初等函数给出解析式的，牛顿法解决不了这个问题。

考虑用数值积分来解决问题，一元函数积分几何意义是函数y=f（x）的图形，在积分上下限区间上与x轴所围成的曲边梯形的面积（图3）。数值积分的目的还是求这个曲边梯形的面积，并且需要满足一定的精度要求。

［a，b］是一个较小的区间，见图4，由于［a，b］区间很小，［a，b］中曲边梯形的面积可以近似采用所示的梯形阴影面积来表示，即∫baf（x）dx≈b-a2［f（a）+f（b）］=（b-a）12f（a）+12f（b），这就是数值计算梯形公式的原理。

上式中a、b称积分点，f（a）、f（b）是积分点对应的函数值，2个“12”是积分点处函数值所占的权重，显然梯形公式的核心是求2个积分点的函数值的加权平均值；加权平均值越接近［a，b］内f（x）的真实平均值，计算精度也就越高。由此想到可以在［a，b］间等距插入有限个节点x0，x1…xn，然后采用合适的权值A0，A1，…，An，然后令（b-a）∑nk=0Akf（xk）更加精确地表达阴影部分的面积，观察上式Ak f（xk）可利用n次拉格朗日型插值多项式构造［4］，得到牛顿-柯特斯公式见式（7）。

I（f）=（b-a）∑nk=0C（n）kf（xk）（7）

C（n）k为柯特斯系数，如n=1时，C（1）0=12，C（1）1=12，这就是梯形公式，当n=2时，C（2）0=16，C（2）1=46，C（2）2=16，这时得到的公式称为辛普森公式［5］见式（8）。

I（f）=（b-a）6f（a）+4fa+b2+f（b）（8）

牛顿-柯特斯公式计算积分的精度不但与区间b-a的大小有关，与区间b-a内所划分的节点数n也有关（n值越大越精确，但n≥8时，牛顿-柯特斯公式计算误差不稳定）［6］，现今对n=2时的辛普森公式研究已经十分成熟，便于编程应用。

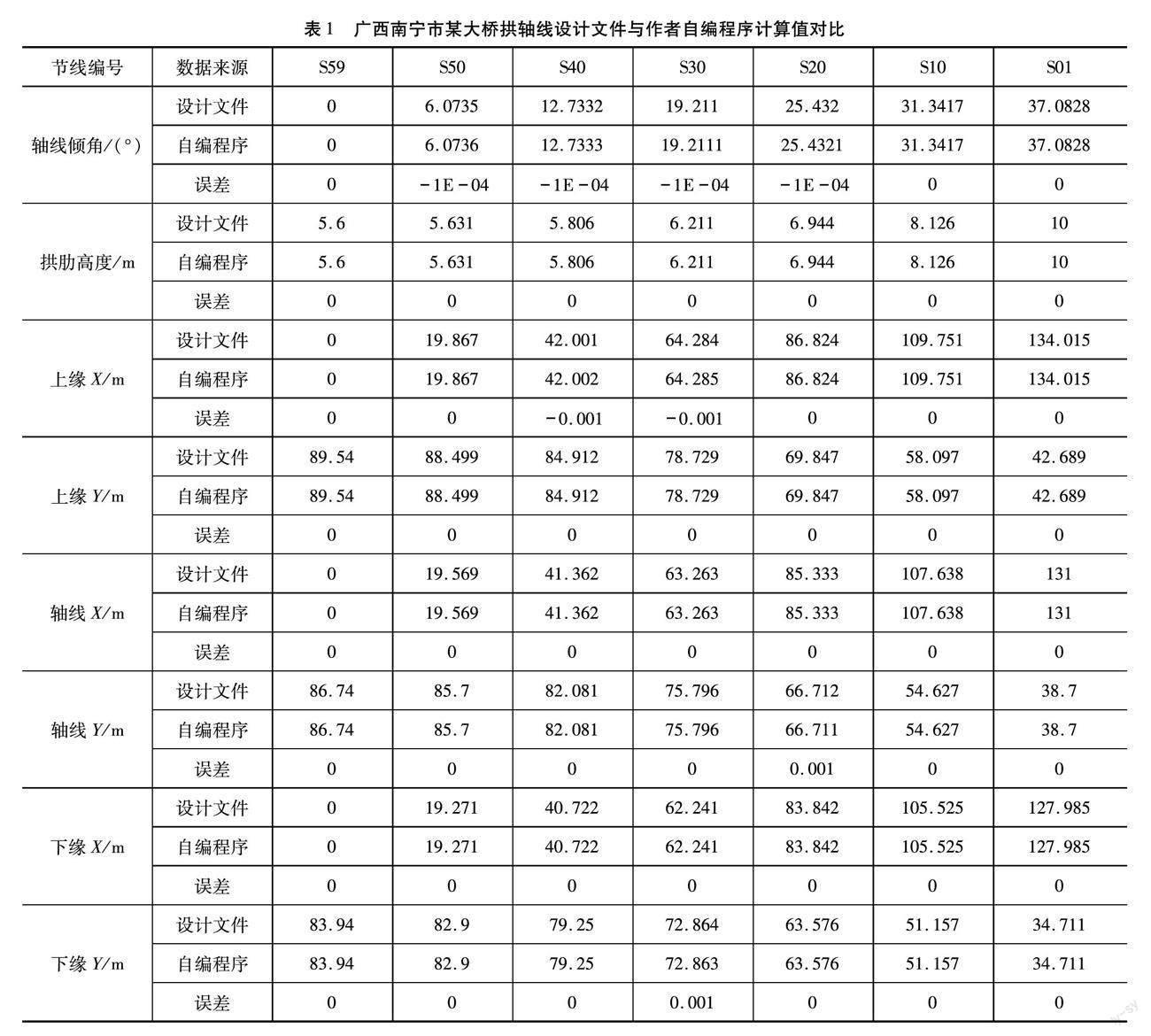
设拱轴线的曲线长度积分区间为［x1，x2］，（x1，x2∈0，l/2，x1

如何控制积分区间的划分是一个重要的问题，令积分区间［a，b］中点为c=a+b2，用S（a，c）表示采用辛普森公式计算区间［a，c］的积分值，S（a，b）、S（c，b）同理表示用辛普森公式计算的不同区间的积分值，由数值分析的知识可以得到S（a，b）的绝对误差近似计算为［4］式（9）。

eps=|S（a，b）-（S（a，c）+S（c，b））|15（9）

将eps作为程序循环计算的精度判断条件，可自行控制计算精度，由此理论完备。

2 程序实现

用Excel中的Visual Basic语言编制程序，曲线长度计算的核心代码如图5所示，代码能实现给定积分区间，返回该区间的悬链线弧长，代码中的yfsenal变量即上述eps，至此引言问题得解。

3 数据验证

笔者找到了广西南宁市某大桥拱肋线形设计图，该桥拱肋高度按照2.5次抛物线变化，由作者自编程序计算得到的拱圈坐标，与设计文件所给坐标对比完全吻合，选取有代表性的7个点对比（表1）。

4 结论

通过数学推导，得出悬链线的曲线长度是不可通过初等函数表达的结论，利用数值分析中求一元函数积分的辛普森公式，在辛普森公式中又引入了复化和自适应的算法，结合Excel中的Visual Basic语言编制成实用的计算程序，程序通过与实桥的设计文件对比验证，论证了理论的正确性，并且达到了足够的精度。桥梁设计是一门综合了数学、力学、计算机科学等多自然学科的综合技术，在桥梁设计工作中，跨学科的综合应用有很多，工程师不可能熟练掌握各个学科的各种理论，因此，工程师们在遇到复杂问题时，需要冷静分析，大胆寻求解决问题的方法，小心求证方法的可行性和正确性，准确有效地解决桥梁设计中的疑难问题，保证桥梁结构安全可靠的使用性能，是广大桥梁工程师的使命。

参考文献

［1］ 顾安邦，向中富.桥梁工程（下册）［M］.3版.北京：人民交通出版社股份有限公司，2017（7）：83，135-137.

［2］ 宋功谭.700m级钢管混凝土拱桥主拱圈构造研究［D］.重庆：重庆交通大学，2021.

［3］ 同济大学数学系.高等数学（上册）［M］.6版.北京：高等教育出版社，2007.4：169-170.

［4］ （美）萨奥尔（Sauer， T.）著；裴玉茹，马赓宇译.数值分析（原书第2版）［M］.北京：机械工业出版社，2014.10：124-126，240.

［5］ 刘佳霖，臧婷.两种定积分数值计算方法的比较［J］.电子技术，2021，50（7）：252-253.

［6］ 林承初.牛顿—柯特斯求积公式稳定性分析［J］.社科与经济信息，2001（9）：172-173.

［7］ 唐珺，楊道杰.自适应积分的递归实现研究［J］.中国高新技术企业，2016（27）：13-16.