加劲钢板剪力墙之加劲肋的优化设计方法
2023-06-29龚小兵唐丽娜樊秦川
龚小兵 唐丽娜 樊秦川


对于仅设置竖向加劲肋的钢板剪力墙的加劲肋刚度,现有的设计规范没有提出明确的控制要求。虽然也有资料提出加劲系数η不小于50的建议,但如何合理适当地设置加劲肋,使其既可以恰当地抑制墙板的整体屈曲,又能尽量减少加劲肋的材料用量和焊接工作量,实现更好的经济性,国内研究较少。通过对门槛刚度的概念解析,对规范计算公式的理解,提出通过临界剪切应力来反推加劲肋刚度的优化设计路径,并提出通过计算小区格的屈曲临界应力来锁定墙板区格划分,提高了加劲肋设计计算的效率,并提出追逐门槛刚度的方法可能不经济适用。
钢板剪力墙; 加劲肋; 门槛刚度
TU392.4 A
[定稿日期]2022-06-15
[基金项目]四川省建筑设计研究院有限公司院内科研项目(项目编号:KY(YN)2018-03)
[作者简介]龚小兵(1968—),男,本科,正高级工程师,国家一级注册结构工程师,研究方向为建筑结构设计。
非加劲薄钢板剪力墙的弹性剪切屈曲临界应力τcr很低,承担较小的水平力就会发生屈曲,钢板产生较明显的面外鼓曲,伴随较大的声响,同时其滞回曲线存在捏缩现象,耗能能力降低,并且其对周边框架的刚度要求较高。
为改善非加劲薄钢板墙的上述问题,学者们借鉴H型钢梁受剪腹板设置加劲肋,以改善腹板稳定性能的方法,对薄钢板设置适当的加劲肋,将薄板分成小区格,顯著地改善了薄板的稳定性能,使其受力性能接近于厚板的表现。同时对周边框架的影响降低,对周边框架的刚度需求也降低。
对钢板进行加劲的方式有多种,如十字、井字、交叉等等,实际工程中,因为层高远小于柱距,故在这样一个框架柱与梁形成的矩形区格中,设置竖向加劲肋对钢板的约束作用最为有效率,同时减少了其它方式中不同方向加劲肋的交叉,使得制作最为简便。本文针对仅设置竖向加劲肋的方式进行研究,其中主要涉及的计算公式依据JGJ99-2015《高层民用建筑钢结构技术规程》[1]附录B.3节。
1 界限刚度的概念
根据文献[1]附录B.3可知:
(1)文献[1]与GB 50017-2017《钢结构设计标准》对加劲钢板剪力墙均是不利用其屈曲后强度,即以墙板的屈曲作为承载能力的极限状态。
(2)墙板的区格高宽比β,有区间要求,即,0.8≤β=hs/αx≤5才能应用文献[1]提供的计算公式,这对划分墙板区格进行了规定,同时,加劲墙板的区格多以高而窄的形式出现,hs/αx多在1~4的范围,可满足上述要求。
(3)文献[1]中提出了参数γτth、加劲系数γ(即加劲肋与墙板的刚度比γ =EIs / Dαx),当加劲系数γ大于等于或小于γτth时,墙板的临界应力τcr分别采用不同的计算公式。文献[1]仅给出了γτth的算法,如式(1)所示,并未给出其含义。
γτth=6ηv(7β2-5)≥6(1)
童根树等[3]给出了算例:
采用双面加劲的方式,如图1所示,钢板hs=3000 mm,a =6000 mm,tb=10 mm,设置3道加劲肋,ax=1500 mm。加劲肋高bs=100 mm,宽bs1=100 mm,厚ts=6 mm,双面加劲。通过改变加劲肋弹性模量E对加劲系数进行变化。钢板剪力墙的τcr-γ曲线如图2所示。
图2是算例剪力墙板的τcr-γ曲线,其中的水平点划线是小区格板块的剪切临界应力(局部临界应力)。从图2中可看出,γ较小时,墙板的剪切临界应力小于局部临界应力,但增长很快;γ在10附近时,墙板的剪切临界应力大致和局部临界应力相等;γ> 11时,墙板的剪切临界应力开始超过局部临界应力,可以认为墙板只发生局部失稳;当γ>25时,墙板的剪切临界应力将以很小的幅度增加,此时再增强加劲肋将没有经济性。
根据以上分析,可以定义当墙板的剪切临界应力等于小区格局部临界应力时的加劲系数值为界限刚度(或称门槛刚度),当加劲系数γ大于等于门槛刚度时,可令墙板的弹性剪切临界应力等于小区格剪切临界应力;而当γ小于门槛刚度时,则令墙板的剪切临界应力取有限元分析结果或规范拟合的公式计算结果。因此,γτth可以定义为界限刚度(或称为门槛刚度)。
图3为算例钢板剪力墙典型屈曲模态,由图3可知,当γ = 1时,墙板为典型的整体半波失稳;随着γ 的增大,但还不足以完全抵抗墙板的面外位移,加劲肋与墙板协同工作,失稳模态表现为相关屈曲,此时亦可称为弱加劲,显然当γ = 5时,为典型的相关屈曲;随着γ 的继续增大,加劲肋的刚度足以抵抗墙板的面外位移,使得墙板在小区格内失稳,失稳模态表现为局部屈曲。
由图3可知,当加劲肋刚度在门槛刚度以下时,加劲肋不足以完全约束墙板的面外位移,加劲肋与墙板协同工作,失稳模态表现为相关屈曲,此时亦可称为弱加劲;而当γ在门槛刚度以上时,加劲肋的刚度足以抵抗墙板的面外位移,使得墙板在小区格失稳,其失稳模态为局部屈曲,相应的此时可称为强加劲。
2 关于最优加劲刚度的求解
综上所述,文献[1]中γτth(门槛刚度)的理论含义,即为对应于小区格稳定临界应力的加劲肋刚度,进一步我们可得到对加劲肋最优刚度设置的求解思路:
(1)先根据结构的整体分析,获得墙板的剪切应力τ,然后根据以下墙板受剪承载力验算式(2)~式(5),逐步反算得到加劲钢板剪力墙所需要达到的弹性剪切屈曲临界应力τcr。
τ≤φsfv(2)
φs≤1.0(3)
φs=130.738+(λn)6(4)
λn=fvyτcr(5)
(2)将(1)得到的τcr作为小区格墙板的弹性剪切屈曲临界应力,按小区格临界应力式(6)~式(8),进一步分析墙板所需要分隔成的区格数量,使其小区格的临界应力不低于τcr。
τcr=τcrp=kτpπ2E12(1-ν2)t2a2x(6)
hsax≥1:kτp=χ5.34+4(hs/ax)2(7)
hsax≤1:kτp=χ4+5.34(hs/ax)(8)
式中:χ为闭口加劲肋时取1.23,开口加劲肋时取1.0;hs为小区格墙板的高度;ax为小区格墙板的宽度(即加劲肋间的净宽度)。
(3)区格划分确定后,假定一个加劲肋构件规格,求得其自由扭转常数Jsy和惯性矩Isy,根据规范提供的公式求得界限刚度γτth,进而根据γ与γτth的大小关系,选择对应的计算公式,计算出对应该规格加劲肋的τcr。
当0.8≤β=hs/αx≤5时,γτth应按式(9)计算:
γτth=6ηv(7β2-5)≥6(9)
ηv=0.42+0.58[1+5.42(Jsy/Isy)2.6]0.77(10)
ax=asnv+1(11)
式中:χ为闭口加劲肋时取1.23,开口加劲肋时取1.0;Jsy、Isy分别为竖向加劲肋自由扭转常数和惯性矩(mm4);ax为在闭口加劲肋的情况下取区格净宽(mm);nv为竖向加劲肋的道数。
当γ<γth时:
τcr=kssπ2E12(1-ν2)t2a2x(12)
kss=kss0a2xa2s+kτp-kss0a2xa2sγγτth0.6(13)
(4)当求得的τcr不满足要求时,则需加强加劲肋的规格,即加强墙板的面外刚度,提高τcr,直至达到小区格局部临界应力。则此时加劲肋的刚度为最优配置。虽然理论上让加劲系数γ去追逐γτth,似乎是最快捷的方式,但是若干算例体现出来,γτth按规范公式计算获得的结果偏大,很可能难以达到或经济性太差。
3 算例
参考图集《钢板剪力墙结构设计》20G122[4]设计钢板剪力墙,如图4所示。
墙板高He=3900 mm,宽Le=3500 mm,厚度tw=16 mm,材质为Q235B,相应的fv=125 N/mm2,fvy=0.58 fy=136.3 N/mm2。
(1)根据结构的整体分析,获得墙板的剪切应力,反求得到墙板所需要达到的τcr:
设V=3486 kN,则τ=V/Letw=62.25 N/mm2
φs =τ / fv = 62.25/125 = 0.498
再由φs ~ λn的关系式,反求λn=1.39
再由λn= (fvy /τcr)0.5,反求得到τcr=fvy /λn2=70.56 N/mm2。
(2)将上一步求得的τcr作为小区格墙板的临界剪切应力,按小区格临界应力公式,分析需分隔成几个区格:
假设加一道加劲肋,分隔成2个区格:
则有hs=3900,ax=3500/2=1750
hs/ax=3900/1750=2.23>1, 采用闭口加劲肋χ=1.23。
按kτp的计算公式,把上述数值代入得到kτp=7.56。
进一步,按τcrp的公式,得到τcrp=117.55,故加一道加劲肋,其分隔出来的小区格临界应力为117.55,具备满足墙板需要的目标临界应力70.56的基础条件。
(3)区格划分确定后,假定一个加劲肋规格,求其Jsy和Isy,根据规范公式求对应的界限刚度γτth,进而计算对应的τcr:
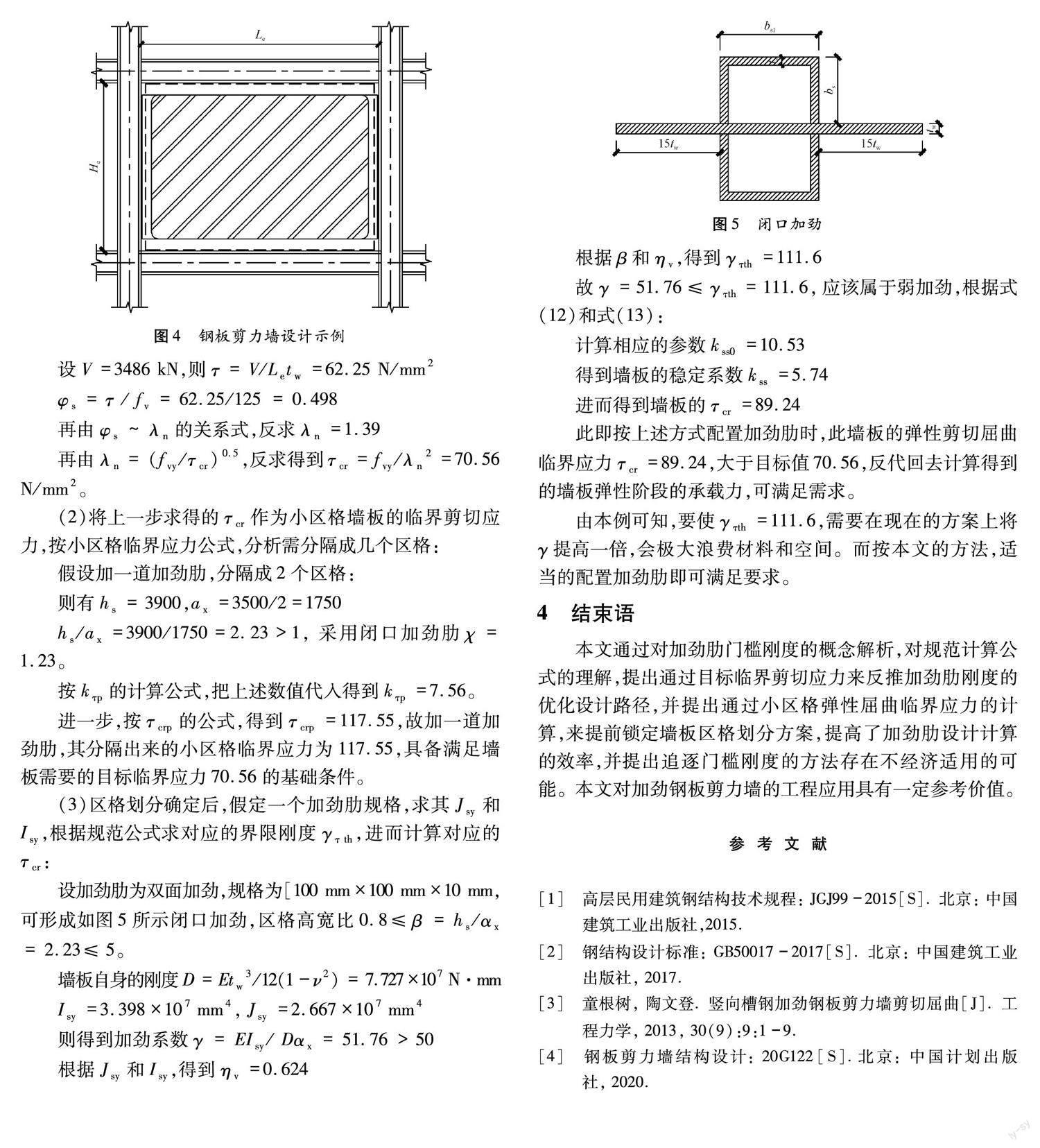
设加劲肋为双面加劲,规格为[100 mm×100 mm×10 mm,可形成如图5所示闭口加劲,区格高宽比0.8≤β =hs/αx = 2.23≤ 5。
墙板自身的刚度D=Etw3/12(1-ν2) = 7.727×107 N·mm
Isy=3.398×107 mm4,Jsy=2.667×107 mm4
则得到加劲系数γ = EIsy / Dαx = 51.76>50
根据Jsy和Isy,得到ηv=0.624
根据β和ηv,得到γτth=111.6
故γ =51.76≤ γτth =111.6,应该属于弱加劲,根据式(12)和式(13):
计算相应的参数kss0=10.53
得到墙板的稳定系数kss=5.74
进而得到墙板的τcr=89.24
此即按上述方式配置加劲肋时,此墙板的弹性剪切屈曲临界应力τcr=89.24,大于目标值70.56,反代回去计算得到的墙板弹性阶段的承载力,可满足需求。
由本例可知,要使γτth=111.6,需要在现在的方案上将 γ提高一倍,会极大浪费材料和空间。而按本文的方法,适当的配置加劲肋即可满足要求。
4 结束语
本文通过对加劲肋门槛刚度的概念解析,对规范计算公式的理解,提出通过目标临界剪切应力来反推加劲肋刚度的优化设计路径,并提出通过小区格弹性屈曲临界应力的计算,来提前锁定墙板区格划分方案,提高了加劲肋设计计算的效率,并提出追逐门槛刚度的方法存在不經济适用的可能。本文对加劲钢板剪力墙的工程应用具有一定参考价值。
参考文献
[1] 高层民用建筑钢结构技术规程: JGJ99-2015[S]. 北京: 中国建筑工业出版社,2015.
[2] 钢结构设计标准: GB50017-2017[S]. 北京: 中国建筑工业出版社, 2017.
[3] 童根树, 陶文登. 竖向槽钢加劲钢板剪力墙剪切屈曲[J]. 工程力学, 2013, 30(9):9:1-9.
[4] 钢板剪力墙结构设计: 20G122[S].北京: 中国计划出版社, 2020.
