从浅层认知到深度理解
2023-06-29季超
季超

[摘 要]数学教学的主要任务应是促进学生思维的发展。“列举策略”教学的核心目标是让学生在自主运用列举策略解决问题的过程中,进一步发展思维的严密性和条理性,使得学生逐步学会更清晰、更全面、更深入、更合理地思考,由“理性思维”走向“理性精神”。
[关键词]列举策略;深度理解;数形结合
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)11-0043-03
一、审题:从“如临大敌”到“因势利导”
“列举策略”单元例1(如图1)的教学依托“围花圃”的真实情境,涉及长方形的等长(周长)变形,对学生来说是有一定难度的。因此,在抛出主问题后,教材编排了问题“根据题中的条件和问题,你能想到什么?”,旨在让学生能分别“从问题想起”和“从条件想起”,想到“周长是22米,可以围成大小不同的长方形”“围成的长方形的长和宽都是整米数”。
然而,真实的课堂不会如教材设计的那样“按部就班”,学生往往会迫不及待地回答:“长与宽越接近,面积越大。”对于这种在教师预设之外的回答,一些年轻教师会感到“如临大敌”,于是选择冷处理;经验丰富的教师则会凭借一些语言技巧“搪塞”过去,等到例1的教学接近尾声时,再请学生来说之前的发现,感觉这样就“功德圆满”了。
针对以上这些教学现象,笔者不禁产生了以下思考。
其一,教材希望学生依据题目条件“用22根1米长的木条围花圃”想到“围成的长方形的长和宽都是整米数”,这有点“强人所难”,因为在生活中,人们完全可以将木材按实际需要进行切割后再使用,更重要的是,即使不明确“长和宽都是整米数”,也完全不影响解题。但是,围成长方形的长和宽如果可以是非整米数,那围法便有无数种了。
其二,学生迫不及待地回答“长与宽越接近,面积越大”恰恰反映了学生的精神追求,即迫切希望自己是一个发现者、研究者、探索者,而教师的主要责任便是以深刻的思想启迪学生。“长与宽越接近,面积越大”这句话有一定的可取之处,但也是不严谨的。作为教师,应当抓住学生回答中的可取之处引发学生进一步思考。
基于上述思考,笔者进行了教学改进。
生1:我觉得长方形的长与宽越接近,面积越大。
师:你认为长方形的面积跟长与宽的相差量有一定的关系,不过要想让你的想法更有说服力,还得怎样?
生1:还要把所有可能围成的情况都列举出来,再比较它们的面积大小。
师:为什么要把所有情况都列举出来?
生1:因为符合“周长是22米”这个条件的长方形有很多种,只有把它们都列出来,才能通过比较找到面积最大的围法。
生2:从中还能判断“长方形的长与宽越接近,面积越大”这样的规律是否成立。
……
在以上教学中,学生在理解题意的环节便说出了“长方形的长与宽越接近,面積越大”。教师不仅认可了学生的说法,还引导学生思考如何进一步证明自己的想法,让学生在自主选择用列举策略解决问题的过程中培育思维的严密性。而教师的提问“为什么要把所有情况都列举出来?”不仅让学生充分感受了列举策略的特点,还让学生将“规律”与“列举”沟通了起来,形成理性思维。
二、探究:“动手动口”终是为了“积极动脑”
通过之前的学习,学生已逐步学会了从条件或问题出发分析数量关系,确定解题思路的策略意识,也充分感受到了列表、画图整理条件和问题的策略价值,具备了初步的策略应用意识。通过教师的引导,学生自然能在列举时使用列表、画图的策略,使得列举过程更为直观清晰、简洁明了。
在解决问题后,教师往往会先问学生有什么发现,当听到学生回答“长方形的长与宽越接近,面积越大”便会心满意足,然后补充说明还需要加个前提条件“周长一定”,最后让学生一同齐读规律。这样的教学使得规律的得出完全是走过场,学生看似读得整齐响亮,实则没能读入心中。究其缘由,是学生在探索的过程中始终只是“动手”“动口”,没有真正“动脑”!
基于上述问题,笔者进行了教学改进。
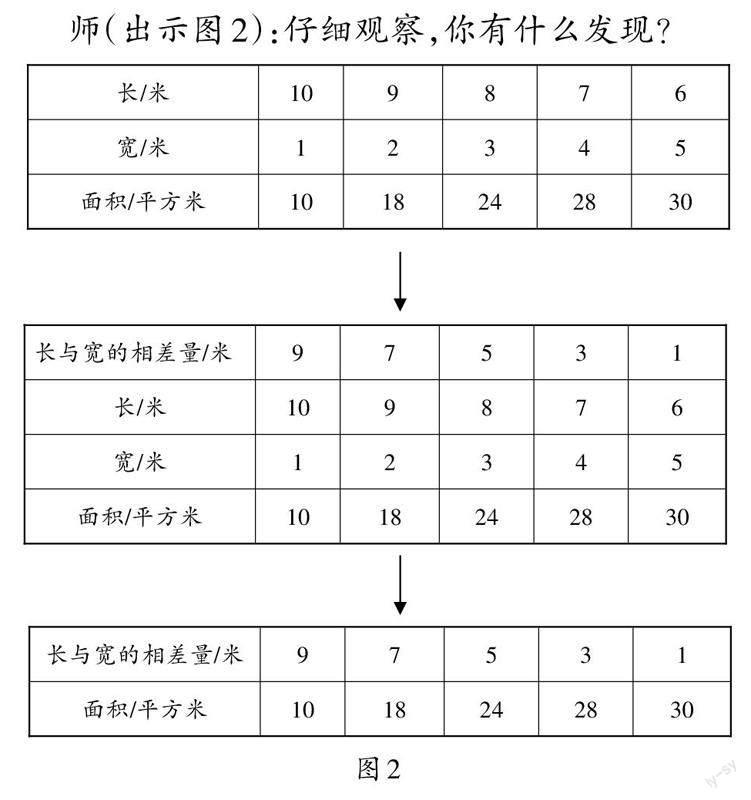
师(出示图2):仔细观察,你有什么发现?
生1:长与宽越接近,面积就越大。
师:你观察到了长方形的面积随着长和宽的变化而变化。学习数学除了要看到变化,还要关注不变。在整个过程中,长方形的什么始终不变?
生1:在整个过程中,长方形的周长不变。
生2:当长方形的周长不变时,长与宽越接近,面积就越大。这样说就更加严谨了。
师:真是这样吗?我们用数据说话。当长10米、宽1米时,长与宽相差多少?……
师:果真如你们所发现的,当周长一定时,面积随着长与宽相差量的变化而变化。
......
在以上教学中,教师并没有急着告知学生前提条件“周长一定”,而是让学生在“变化”中找寻“不变”,即在不断变化的数中找准其中的不变因素。通过对规律的不断剖析,学生逐步想得更全面、更合理,思维的综合性由此得到提升。
课程标准指出:“在教学过程中,教师要重视数学结果的形成过程。”换言之,充分感受规律得出的过程比规律本身更为重要,教师不应以单纯的寻找规律作为策略教学的拓展路径,而应充分处理好过程与结果的关系,让学生的直接经验与间接经验得到有效的沟通整合,帮助学生逐步学会更清晰、更全面、更深入、更合理地思考,努力促进学生思维的发展。
三、深化:数形结合,让规律可视化
“在理性思维与理性精神背后同样隐藏着火热的激情:一种希望,揭示世界最深刻奥秘的强烈情感。”这就需要教师处理好直观与抽象的关系——对抽象的数学内容进行深入剖析,并以直观的形式加以展示。在之前的学习中,学生在比较不同列举方法的过程中已经初步感知到了数与形之间的对应关系,当然,这种对应关系相对来说是比较简单的,因为之前的数代表的只是长与宽的长度。在学生得到规律后,此时表格中的数代表的含义变成了长与宽的相差量以及对应的面积。此时,基于函数思想,同样可以用直观的图形来表示抽象的数乃至规律。
基于上述思考,笔者进行了教学改进。
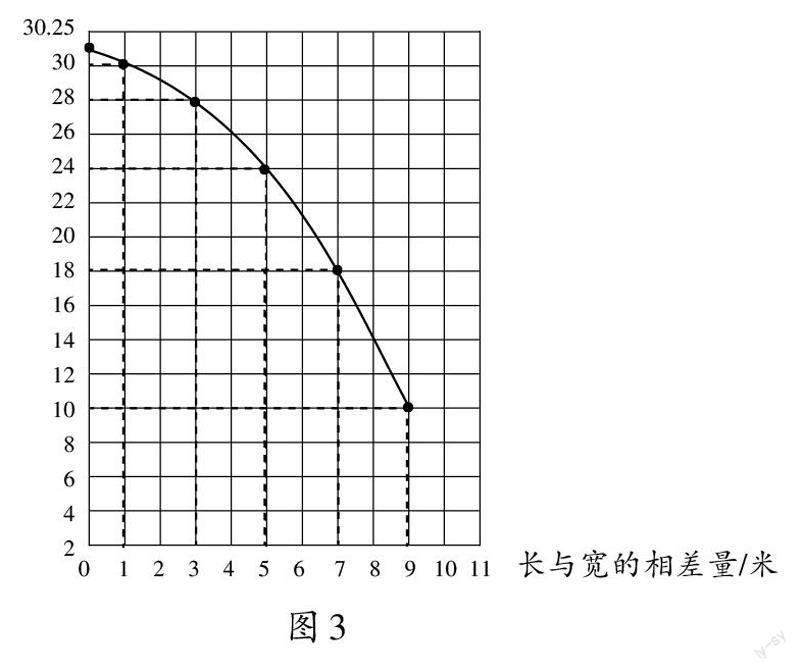
师:这里同样可以用直观的图形来体现数的变化。用横轴表示长与宽的相差量,越往右代表相差量越大;用纵轴表示长方形的面积,越往上表示长方形的面积越大。
师(描出其中一个点):当长与宽的相差量是9米时,对应面积是10平方米,可以用1个点来表示此时长方形的面积和长与宽相差量之间的关系。
师(指名学生依次指出剩下4个点的所在位置,如图3):我们得到了这5个点,把它们连起来,就能得到这样一条曲线。看着这条曲线,你有什么发现?
生1:这条曲线的变化趋势更加直观地说明,当面积一定时,长与宽的相差量越大,面积越小;长与宽相差量越小,面积越大。
师:是啊,看来学习数学的时候,将数与形结合起来,能更直观地发现变化规律。
生2:我觉得这条曲线还可以往左边延伸,一直延伸到纵轴,到纵轴这个位置,就相当于长与宽相差0米,此时它就是一个正方形,边长为5.5米,通过计算得出面积是30.25平方米。在所有的长方形中,这是面积最大的情况。
师:有什么新的想法?
生3:围法可以有无数种,只是因为我们是用“1米长的木条”围的,长与宽必须是整数,所以刚才只列举出这五种情况。
生4:如果没有这个条件,就不能把所有情况一个一个列举出来了。
师:这条变化趋势线的出现,离不开最初的这5个对应点,而这恰恰是我们通过一一列举得到的。看来一一列举的策略不仅可以帮助我们解决问题,还可以帮助我們发现规律。
“具体解题策略的学习”与“普遍性思维策略的学习与思维品质的提升”是相辅相成的。教师的推理性提问和启发性提问,能引导学生迸发出思维的火花,从而实现对规律的深度理解。策略教学的深化不应被理解成形式的变化,而是“由简单走向复杂,化复杂为简单”。这也为学生具体学习各种解题策略,特别是普遍性思维策略,以及提升思维的品质,提供了重要途径。
笔者通过课前调查发现,有不少学生对“周长一定时,长方形的长与宽越接近,面积越大”这样的规律有了一定的感知,但这样的感知往往是模糊的、不严谨的。如何突破学生的浅层认知,促使学生对教学内容深入理解,就需要教师在课堂实践中把握好过程与结果的关系、直观与抽象的关系以及直接经验与间接经验的关系。
其一,重视数学结果的形成过程。不仅让学生能较严谨地说出规律,还要使学生了解规律是如何得到的。列举策略不仅可以研究“周长一定时,面积和长与宽的相差量之间的关系”,还可以研究“面积一定时,周长和长与宽的相差量之间的关系”,乃至“长方形一边靠墙时,面积和长与宽的相差量之间的关系”。值得注意的是,在教学中,规律本身并不重要,重要的是引导学生充分参与规律的得出过程,并从中发展思维的严密性和条理性。
其二,重视数学内容的直观表述。在上述教学案例中,教师充分运用几何直观帮助学生思考,培养学生的推理意识:由5个关系点得到一条变化趋势线,将抽象的数字转化成了直观的图形,依托曲线的变化,更为直观地证明了规律的合理性。
其三,重视学生直接经验的形成。在教学案例中,教师既没有急着结合变化趋势线按部就班地授课,也没有把其当作“噱头”一带而过,而是设置了开放性问题,以启发学生自主探索和发现。学生的思维随之打开,自然而然想到了这条曲线可以朝着另一个方向继续延伸,感受到符合“面积一定”围法的无限性,只是受限于题目的具体条件“1米长的木条”才只能列举出五种不同的情况。如此,学生对题目的条件有了更加深刻的认知,感受到列举策略不仅能解决问题,还能找出规律。此时,学生的认知由“理性思维”走向“理性精神”。
苏霍姆林斯基曾说:“人的心灵深处都有一种根深蒂固的需要,就是希望自己是一个发现者、研究者、探索者,而在儿童的精神世界里,这种需要特别强烈。” 数学教师应由强调各种具体解题策略转变为注重学生普遍性思维策略与思维品质的提升,帮助学生通过解决问题逐步想得更清晰、更深入、更全面、更合理,从而不断提升思维的综合性、灵活性、自觉性和创造性。
[ 参 考 文 献 ]
[1] 郑毓信 .传统应用题教学之当代重建(上)[J].中小学课堂教学研究,2020(1):3-7.
[2]郑毓信 .教育之哲学审思:哲学视角下的数学教育(二)[J].江苏教育,2022(17):25-30.
[3] 孙保华.丰盈教学过程 感受策略价值:“解决问题的策略(列举)”教学设计与说明[J].小学数学教育,2015(22):48-49.
[4] 郑毓信 .数学教师应有的“文化担当”(中)[J]. 湖南教育(C版),2019(2):22-24.
[5] 郑毓信 .从“反思性实践者”到“作为研究者的教师”(上)[J].小学教学(数学版),2018(Z1):40-47.
(责编 金 铃)
