基于深度长短期记忆网络的地表温度预测

董健明，陈 雨

（四川大学电子信息学院，成都 610065）

0 引言

地表温度是决定地表能量平衡和获取地表能量交换信息的重要因素，也是地球科学研究不可或缺的重要参数，涉及众多基础学科研究［1］。1999 年和2002 年，美国宇航局分别发射了两颗搭载了MODIS 中分辨率成像光谱仪的极地轨道遥感卫星Terra和Aqua，这两颗卫星为快速获取区域地表温度信息提供了新的途径，并确保了获取此类数据时的连续性［2］。由卫星搭载的MODIS 所处理并获取的地表温度数据［3］，已经在包括植被监测、干旱评估、地热勘测和火灾检测在内的众多科学领域发挥了重要的作用［4-7］。但是由于这些卫星系统是被动遥感系统，云覆盖对地表温度的估计和信息提取不利，地表温度数据可能会出现缺失，进而导致在进行灾害预警和农业监测时无法做出准确预测。因此在分析地表温度的时空信息时，需要考虑到数据不完整、不准确所带来的影响［8］。

为了得到完整准确的地表温度数据，部分学者提出了结合大气参数（如透射率和温度）或地表参数（如发射率和几何形状）的地表温度反演方法［9-11］。除了这些传统方法外，一些研究人员还利用人工神经网络（artificial neural network，ANN）来获取地表温度数据。由于传统方法不会去分析建模中涉及的变量之间不完全已知的关系，并且建模和计算过程较为繁琐，因此人工神经网络相比传统方法的建模过程更为简洁且结果更为精确［12］。虽然已有很多研究采用人工神经网络的方法利用各种变量作为输入对地表温度进行建模、模拟或预测［13-14］，但是人工神经网络的方法无法提取基于时间的特征。相较于人工神经网络来说，基于时序的深度神经网络尝试从序列中获取数据的时序特征，每个神经元的输出也会作为输入反馈回其本身，从而这些神经元具备了先前输入的一种“记忆”。因此对时间序列做预测时，时序神经网络的效果要优于人工神经网络［15］。

在时序神经网络中，基于循环神经网络（recurrent neural network，RNN）所改进的长短期记忆网络（long short-term memory，LSTM）在1997 年被Hochreiter 等［16］提出，它克服了RNN无法记忆长期时序特征进而在时间序列较长时的预测准确率不高的问题，长期时序数据的预测效果得到显著提升。基于LSTM 的时间预测模型在包含地表温度在内的众多领域得到了应用，比如将LSTM 改进成混合数据驱动后的模型对日地表温度数据序列的预测达到了很好的效果［17］，在自然灾害方面，利用LSTM 对MODIS 卫星图像研究可以对森林火灾达到85%的准确率检测［18］，以及LSTM对海面温度也能进行有效的预测［19］。目前关于LSTM 在MODIS 数据方面的预测大多数还采用单层LSTM 结合其他理论方法或对单层LSTM 进行内部结构的改进。然而，在单层情况下某些时间序列信息的复杂特性是无法被直观表述的，想要提取这些深层特征以提高整体的性能便需要着眼于LSTM 可以堆叠成深层网络的特点。本文从MODIS 月时变栅格数据中提取了多点地表温度时间序列，并得到研究区域的月平均时间序列；通过对LSTM 堆叠构成深度LSTM 网络，使用遗传算法来预训练优化网络结构，再对地表温度数据进行预测，并将该模型和其他时序预测网络模型进行对比，验证深度LSTM网络的预测性能。

1 地表温度数据提取

本文原始数据采用美国国家航空航天局在LAADS（Level-1 and atmosphere archive&distribution system）DAAC（distributed active archive center）网站接口提供的MODIS-Level-3 数据集，包含2000年1月至2021年8月共260个月份的分辨率在0.05 度纬度/经度气候模拟网格（climate modeling grid，CMG）数据。

MODIS 的Level-3 数据即第3 级数据是将卫星测得的原始数据处理过后得到的校正后数据。0级产品被称为原始数据，在其基础上赋予标定参数后为1 级产品Level-1A 数据，通过对Level-1A 数据进行MODIS 传感器数据的辐射校准后可得到Leve-1B 数据即2 级产品，其为定标定位后的数据，采用国际标准的EOS-HDF（earth observation system-hierarchy data format）格式，包含所有波段数据且应用广泛。而3级产品在1B数据的基础上，对由遥感器成像过程产生的边缘畸变（Bowtie 效应）进行校正，产生Level-3 级产品。将得到的260 个月份的Level-3数据集通过HEGTool 工具处理，可将包含多种类型的数据的HDF 文件处理为记录了许多图像信息的TIFF 格式文件。对此格式的文件，用ArcMap 软件在本实验的研究地区——美国得克萨斯州休斯顿地区进行地表温度信息数据的提取，最终对研究地区所取的采样点取平均可以得到实验所需的260个月的地表温度时序数据。

2 模型搭建

2.1 LSTM网络结构和原理

时间序列由于其复杂的特征，导致基于统计学的传统预测方法难以得到较好的预测效果。循环神经网络RNN 提供了一种全新的预测时间序列的方法，但是它自身在训练的过程中容易造成梯度爆炸或消失进而造成权重震荡，导致它无法克服短时依赖特征，因此在循环神经网络RNN 模型的基础上，为了解决其在长期记忆的情况下丧失学习能力的问题，Hochreiter 等［16］提出了LSTM 网络，这是一种特殊类型的RNN网络，它可以学习长期依赖信息。循环神经网络的当前时刻输出不仅与当前时刻输入有关，还与上一时刻的状态有关，RNN 的网络模型结构较简单（见图1），它可以记录时间序列信息，RNN单元的计算公式如下：

其中：ht-1表示上一个时刻的隐藏层状态；Xt是当前时刻的输入值；Wh和bh分别表示当前层的权重和偏置；tanh 激活函数可以将流经网络后输出的值控制在-1和1之间。由公式（1）可以看出，RNN 此时刻的隐藏层信息只来源于当前输入和上一时刻的隐藏层信息，并没有长期记忆的功能。

图1 RNN模型结构

LSTM 网络模型结构改进的核心点在细胞状态，它在运算时只有一些少量的线性交互，信息在传播时想保持不变也就比较容易。决定细胞状态应该保留哪些信息和更新哪些信息的核心是LSTM 中的门结构，它实现了一种让信息选择性通过的方法，门结构包括一个Sigmoid 神经网络层和一个按位运算的乘法操作，LSTM 的内部结构如图2 所示。在LSTM 模型的门结构中，第一步遗忘门的输出ft会取决于上一个时刻隐藏层的状态ht-1和当前输入Xt，它将决定上一时刻的细胞状态Ct-1中的哪些信息应该从模型中舍弃。更新门将确定哪些新信息会被存放在细胞状态中，之后将旧的细胞状态Ct-1更新为新的细胞状态Ct需要遗忘门和更新门的共同作用。最终，输出的ht将会基于当前的输入Xt和细胞状态Ct而决定，其中具体的计算公式如下所示：

上式中，σ为Sigmoid 激活函数；W、b分别为不同层的权重和偏置；ht是当前时刻的隐藏层状态值。

图2 LSTM结构

2.2 深度LSTM网络

单层的LSTM 网络在使用中虽然可以解决RNN 的长期依赖问题，但是很多时候由于网络的层数少，有些时间序列信息的复杂特性无法被直观表述，例如当对一些线性度不高或者时间记忆间隔很长的数据进行处理时，增加神经网络的深度就是提高整体性能的有效方法［20］。RNN 可以看作是一个随着时间增加而不断增加堆叠层数的网络模型，同时可以从输入层—隐藏层、隐藏层—隐藏层、隐藏层—输出层三个角度将RNN 扩展成深度RNN 网络［21］。本文所提出的深度LSTM 网络模型（DLSTM）是指对LSTM的结构进行多个的堆叠，如图3所示，在这种分层架构中堆叠多个LSTM的目标是在较低层构建特征，从而分离输入数据中的变化因素，然后在较高层组合这些特征。循环网络一层一层的堆叠增加了隐藏层的层数，意味着增加了输入在循环结构中不同的时间尺度上所能学到的特征。

图3 DLSTM网络体系结构

在图3所示的DLSTM 体系结构中，在t时刻的输入Xt和上一时刻的隐藏层的状态作为第一个LSTM 结构的输入，在t时刻的隐藏状态的计算见2.1 小节，向前进入第二个循环网络结构，将之前的隐藏状态和前一步的隐藏状态输出作为当前输入来计算，继续向前进入之后的LSTM 结构块，以此类推直到最后一个LSTM结构。

这种堆叠架构的一个好处是，每一层都可以处理任务的一部分，然后将其传递到下一层，直到最后一个累积层提供输出。另一个好处是，这种结构可以让每一层的隐藏状态在不同的时间尺度上运行。在显示使用具有长期依赖性的数据的场景中，或在处理多变量时间序列数据集的情况下，有较好的效果［22］。除此之外，隐藏层和输出层之间有深层的结构，有助于更加高效地汇总之前的输入，从而促进最后预测结果的输出，因此在最后一个LSTM 结构之后添加了一个全连接Dense层加深隐藏层与输出层之间的深度。与RNN神经网络一样，LSTM的网络结构也得益于激活函数和抑制过拟合的方法，本文在每一层LSTM 都加入了Dropout 层，并且选择tanh 函数作为非饱和激活函数，作为防止过拟合的手段。

3 模型训练

3.1 原始数据的处理

由于实际的时间序列是非平稳的，很多时候可能表现出某些特定的趋势特征［23］。而静态数据对于模型的建模来说更容易，而且会有助于更高效地产生预测结果。所以在数据的预处理中，首先需要删除数据中的趋势属性，无论是增加还是减少的趋势。之后，实验会将这种趋势返回数据中，以便将预测问题返回到原始数据中。消除趋势的标准方法是对数据进行差分，即从当前时刻（t）的数据中减去上一时间步（t-1）的观测值。预测方面，本实验采用的是时间步长为1 的预测，即预测下一个时间（t+1），具体是利用滞后时间方法将时间序列分为输入和输出，利用前几个时间点的数据作为预测输入，来预测下一个时间点（t+1）的输出。本实验中，滞后时间选取在1～8个时间步长。

与其他神经网络一样，DLSTM 希望数据范围在网络使用的激活函数范围内。LSTM 的默认激活函数是双曲正切函数，其输出值介于-1 和1之间。这是时间序列数据的首选范围。在这之后，实验会将缩放后的数据转换回原尺度，以便将预测问题返回到原始数据中。

食品药品安全是重要的民生工程，行政监管和技术支撑是“双轮驱动”，食品药品检测人才队伍是食品药品检测体系的重要组成部分。近年来大批应届毕业生或是相关专业背景的非系统内人员进入食品药品检测实验室，为食品药品检测事业提供新鲜血液。本文结合新进人员培训的实际工作和宏观科学，包括社会学、管理学、心理学、人才学等经典理论，为更好地培养科室技术队伍提供一些经验和方法。以下分别论述科室岗前培训中的各个组成要素和四个阶段的特点。

3.2 超参数的确定

本文模型训练的超参数主要包括训练过程中选取的epoch 数，即需要将完整的数据集输入进网络进行训练的次数、每一个LSTM 层所选取的神经元个数，以及时间间隔步长，也就是预测下一个值所需之前数据的滑动窗口长度。选取时间间隔步长作为超参数之一是因为时间序列的预测问题在输入之前时间的数据时也意味着添加了噪声，所以在训练模型的时候，可以选择使用不同的时间间隔步长来找到规律从而更为精准地预测。在本文中，超参数的选取采用的是遗传算法来进行实现的。

DLSTM 模型的实验包括两种场景，即静态场景和动态场景。在静态场景中，使用所有训练数据拟合预测模型，然后用真实的测试数据预测下一个时间的值。在动态场景中，通过在测试数据中插入之前的预测值，在每个时间更新预测模型。而静态预测使用实际值对每个后续结果进行预测。超参数的数量取决于实际场景。对于静态场景，有三个超参数，即epoch数、每层隐藏神经元数和时间间隔步长。对于动态场景，多了一个更新次数update，即在测试数据中插入预测值时，每个时间更新预测模型的次数。本实验将网络结构分为1、2、3、4、5 层LSTM 结构，每一层LSTM 神经元个数的选择范围是1～32，epoch数选取在100～2000，滑动窗口步长范围为1～8，动态场景下update 范围为1～4，将每种结构结合神经元个数、epoch数和滑动窗口步长进行种群的生成，随机产生5个种群进行选择、交叉、变异的遗传进化，经过10 代后得到最优解，最终总结根据评价指标（见4.1小节）选择出静态场景（表1）和动态场景下（表2）的每种结构的最优解，从而得到它们分别应该选取的模型的超参数。

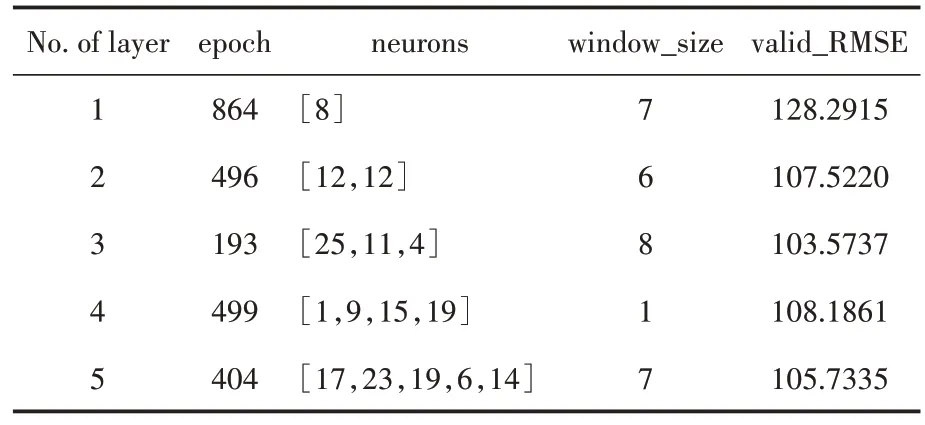
表1 静态场景下DLSTM模型的超参数

表2 动态场景下DLSTM模型的超参数

3.3 模型训练环境

在本文的模型训练阶段，采用了GA（genetic algorithm）遗传算法，使用的是Python 库中的分布式进化算法实现的遗传算法（distributed evolutionary algorithms in Python）。GA 算法是根据达尔文的生物进化论和自然选择理论所提出的一种模拟生物种群选择、交叉、变异过程的局部最优解搜索方法。模型的运行环境为基于Tensor-Flow机器学习算法库搭建而成，所使用的Tensor-Flow 版本为2.3.0，代码编写所使用的环境为Python3.8，权重优化器选择为Adam 优化器，所用训练集数据占全数据集的80%，共208 个月，剩余52个月份用作测试集数据。

4 实验结果及分析

4.1 模型评估标准

4.1.1 均方根误差

均方根误差（root mean square error，RMSE）常常用作深度学习模型的评价指标，误差值的尺度和数据本身相同，因此直接基于该误差的精度度量不能用于在不同尺度的序列之间比较。均方根误差的取值是预测值与真实值偏差的平方和与观测次数n比值的算术平方根，其表达式如下：

均方根百分比误差（root mean square percentage error，RMSPE）作为一种百分比误差，优点是与原数据尺度无关，所以常常被用作不同尺度数据集的预测评价指标，其计算式如下：

使用这两个指标得到的结果在计算值上是不同的，但在预测模型的性能度量中，每个指标的显著性是相似的。值得注意的是，由于数据在大多数情况下呈现不同的尺度，因此最好使用RMSPE或任何其他百分比误差度量来估计不同模型之间的相对误差。

4.1.2 平均绝对百分比误差

平均绝对误差（mean absolute error，MAE）表示预测值和观测值之间绝对误差的平均值，MAE是一种线性分数，所有个体差异在平均值上的权重都相等，所以RMSE相对MAE来说，对于误差高的预测值惩罚更多，计算公式如下：

同样，平均绝对百分比误差（mean absolute percentage error，MAPE）作为平均绝对误差的百分比形式，公式如下：

4.2 实验结果分析

本小节将会根据之前选取的超参数对研究区域的地表温度数据采取层数不同的LSTM 模型训练评估，通过对几种不同的模型结果进行比较，确保对提出的DLSTM 模型进行真正公平的评估。评估模型的性能时并非只用到了一个评价指标，百分比误差被证明在评估不同模型的性能，特别是在数据集的尺度大小不一样时是最适合的工具［24］。所以本小节将会依据百分比误差来对几种模型的实验结果进行分析。

将实验的模型预测方式分为动态更新和静态更新两种，表3 为DLSTM 模型在动态模式下的各个模型评价指标的计算结果，表4为静态模式下的模型评价指标值。总结表3 和表4 的结果可以看出，静态更新模式下的结果要优于动态更新模式，这种情况是符合事实预期的，因为在动态更新模式下，预测结果的偏差值可能会在下一时序预测的时候被放大和产生误差的累积，影响后续的预测结果。

表3 动态模式下评价指标的计算结果

表4 静态模式下评价指标的计算结果

除此之外，动态模式下的预测结果曲线图和静态更新模式下的预测结果分别如图4 和图5所示。

图4 动态模式下的预测结果

图5 静态模式下的预测结果

通过对比相同更新模式下的不同层数评价指标值可以看出，和单层的LSTM 模型结构相比，特别是动态模式下，DLSTM 的模型评价结果要更优，这也说明了对地表温度数据通过堆叠LSTM 网络结构的方法来预测的效果要优于单层模型。从网络结构来看，DLSTM 相比单层来说含有更多的网络结构，这也表明了深层次的网络结构更容易从时间序列中提取到时间特征，也就体现为DLSTM 在时间预测方面有更好的效果。同时对比多层模型结构下的评估指标，层数的增多并不会带来实验结果的显著提升。

5 结语

本文将一个可以用于大多数时间序列预测问题的模型——LSTM 网络模型进行深层次的构建，得到了DLSTM，即深度长短期记忆网络，并将其用于美国德克萨斯州休斯顿地区2000 年1月至2021 年8 月共260 个月份的地表温度预测。DLSTM 网络模型通过堆叠LSTM 模型并且在输出层添加线性全连接层来增加模型的层数结构，模型的时间步长、神经元个数等超参数采用遗传算法进行优化选取。实验结果标明，DLSTM网络对此地区的月时序地表温度数据有良好的预测效果，同时深层的网络模型具有更多的网络结构，能更容易从时间序列中提取到时序特征，实验结果要优于单层的网络模型结构，在时间序列数据的预测问题上表现更为优异。

鉴于当前研究中存在的不足，可以进行后续更深入的改进。本文的实验数据序列的选取较为单一，暂未考虑降雨、蒸散发等其他气候因素的影响，因此在后续具体区域的研究中应加入其他因素的影响，得到更为精确的实验序列再进行实验的训练和预测。另外，随着搭载MODIS 的卫星围绕地球所测得的时间序列增多，意味着会对实验提供更加丰富的训练数据集，相信深度神经网络在这方面的预测也会更为准确。