多普勒积分辅助BDS三频周跳探测

王建敏，王清旺，黄佳鹏

多普勒积分辅助BDS三频周跳探测

王建敏，王清旺，黄佳鹏

（辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000）

针对单频多普勒积分对低采样率数据周跳探测精度较低的问题，提出一种基于北斗卫星导航系统（BDS）三频观测数据的多普勒积分辅助伪距相位组合的周跳探测方法：利用多普勒积分计算历元间伪距变化量，大大减弱多路径效应的影响；并通过选择最优的三频组合系数构造宽巷相位和窄巷伪距组合周跳检测量，提高多普勒积分对低采样率数据的周跳探测精度。实验结果表明，提出的组合方法可以弥补各自的周跳探测盲点，对于不同采样率数据，不仅能有效探测和修复大小周跳、连续周跳和不敏感周跳，还可以准确地辨别1个周期以上的周跳和粗差，具有良好的周跳探测性能。

周跳探测；北斗卫星导航系统（BDS）；多普勒积分；伪距相位组合

0 引言

随着北斗三号的全面建成，北斗卫星导航系统（BeiDou navigation satellite system，BDS）在社会生产建设中的地位越来越重要。用户可以利用多频BDS卫星观测数据进行高精度定位。在数据处理过程中，周跳的探测和修复是确保定位精度的关键之一[1]。传统的周跳探测方法主要有高次差法、多项式拟合法、墨尔本-维贝纳（Melbourne-Wübbena，MW）组合法、伪距相位组合法、电离层残差法和电离层残差二次差（second-order time-difference phase ionospheric residual，STPIR）法等，这些方法都是基于伪距和载波相位观测值构造周跳检测量进行周跳探测。其中高次差法在作差的同时也放大了观测噪声的影响，不能探测较小的周跳[2]。多项式拟合法的周跳探测精度取决于拟合系数，且对低采样率数据的周跳探测精度逐渐降低[3-4]。MW组合法和电离层残差法均有各自的周跳探测盲点，二者联合起来可以弥补各自的不足，是目前较好的双频周跳探测方法[5-7]。伪距相位组合法适用于三频周跳探测，但周跳探测精度受伪距观测噪声影响较大[8-10]。STPIR法通过对电离层残差周跳检测量在历元间进行二次作差，进一步减弱了电离层变化对周跳探测的影响[11-12]。除此之外，多普勒积分法也常用于单频周跳探测，但其对低采样率数据的周跳探测精度较低。目前大量的研究也对多普勒积分法进行了改进，如利用多普勒积分辅助伪距相位组合进行单频周跳探测；利用卫星星历重构多普勒积分值，并联合STPIR法进行双频周跳探测，提高了多普勒积分法的周跳探测能力[13-14]。

在利用多普勒观测值进行周跳探测时，周跳探测精度取决于多普勒观测值的精度和数据采样率[15]。虽然多普勒观测值的精度远大于伪距观测值，但随着采样间隔的增大，多普勒积分误差增大，导致周跳探测精度降低。本文基于多普勒和载波相位观测数据，提出了多普勒积分辅助的三频伪距相位组合法，首先利用多普勒积分值计算历元间伪距变化量，再计算历元间载波相位变化量，并通过选择最优的三频组合系数构建宽巷相位和窄巷伪距组合周跳检测量，最后利用该方法联合STPIR法进行周跳探测，以此减弱多普勒积分误差对周跳探测精度的影响，提高多普勒积分对低采样率数据的周跳探测能力。

1 基本原理

1.1 多普勒积分

多普勒观测值是瞬时载波相位变化率[13]，其计算公式为

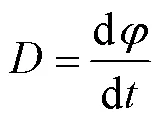
可以利用多普勒积分值计算历元间的载波相位变化量，即

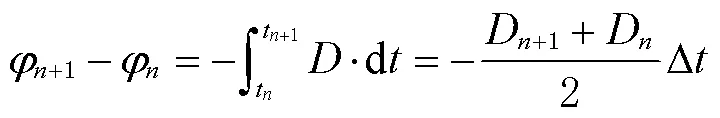
由于式（2）中计算出来的载波相位值不含周跳，因此可以用来探测周跳。用多普勒积分值计算的历元间伪距变化量为

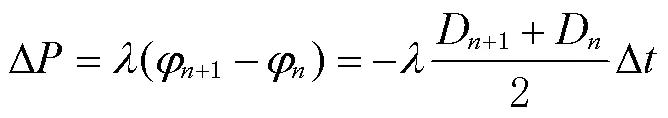
式中：Δ为历元间伪距变化量；为对应频率的波长。

1.2 多普勒积分辅助三频伪距相位组合

构建三频伪距和载波相位组合观测方程[16]，表达式分别为：

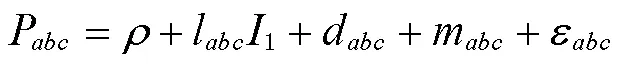
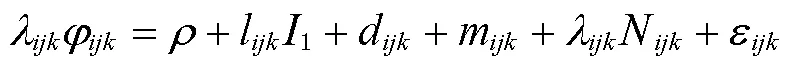
将式（4）代入式（5）中，求得相位组合观测量的整周模糊度为

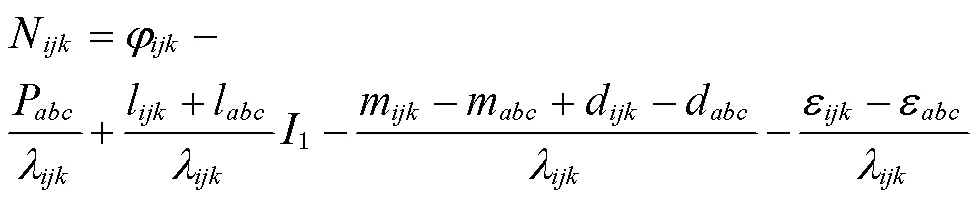
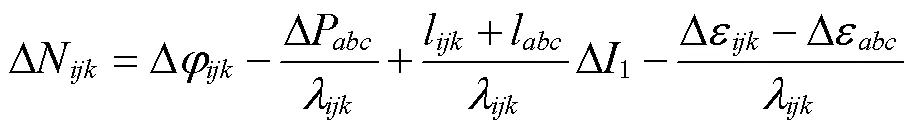
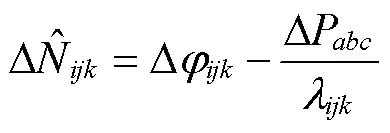
根据多普勒积分辅助的伪距相位组合系数可得周跳检测量中误差为

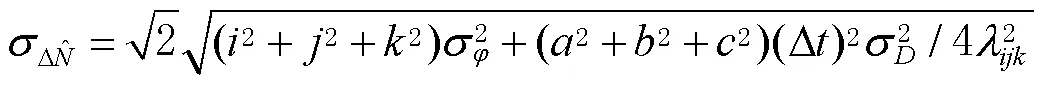
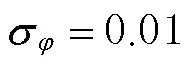
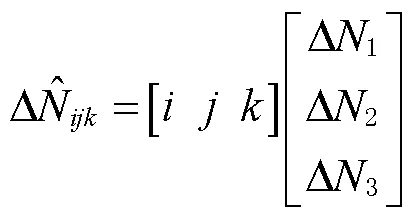
1.3 STPIR法

由于电离层残差受采样间隔影响较大，对于低采样率数据，对电离层残差在历元间作二次差的方法降低了电离层的时间变化趋势，也可以大大减弱或消除电离层误差、对流层误差以及卫星钟和接收机钟的钟差[17-19]。

以组合系数（1，1，-2）构建三频电离层残差组合观测量[20]，表达式为

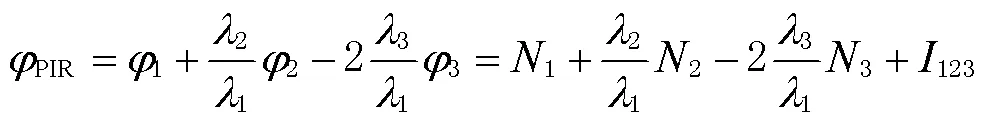
将式（11）在历元间作差，得到三频电离层残差组合周跳检测量，表达式为

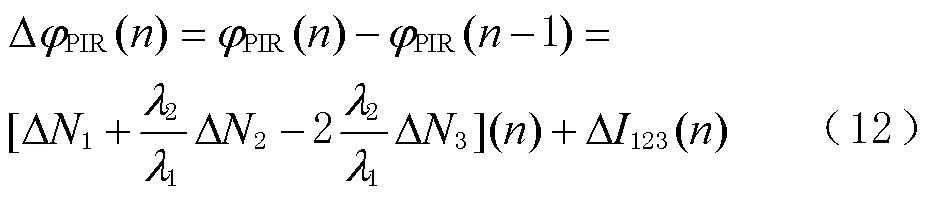
假设观测数据起始2个历元无周跳发生，将电离层残差周跳检测量在历元间二次作差，即可得到STPIR法的周跳检测量[20]，表达式为

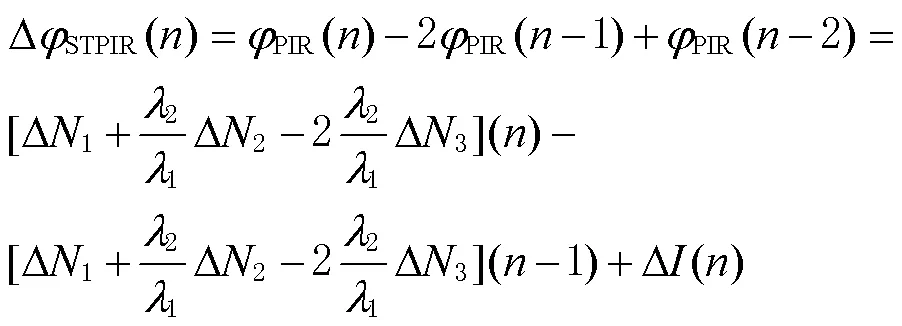
STPIR法周跳检测量中误差为

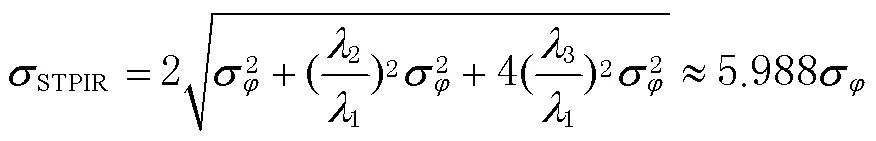
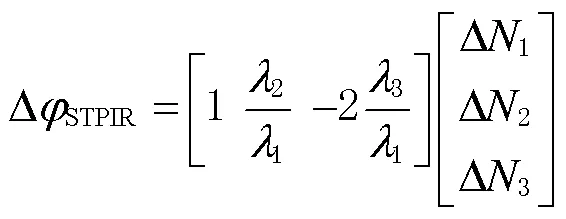
1.4 最优组合系数选取

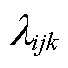
伪距相位组合周跳检测量的电离层延迟系数可表示为

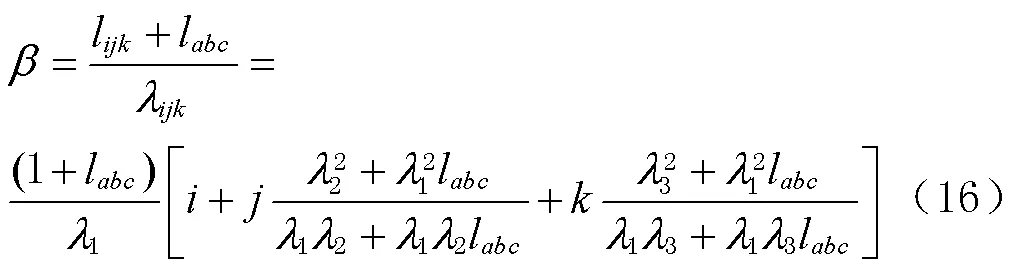
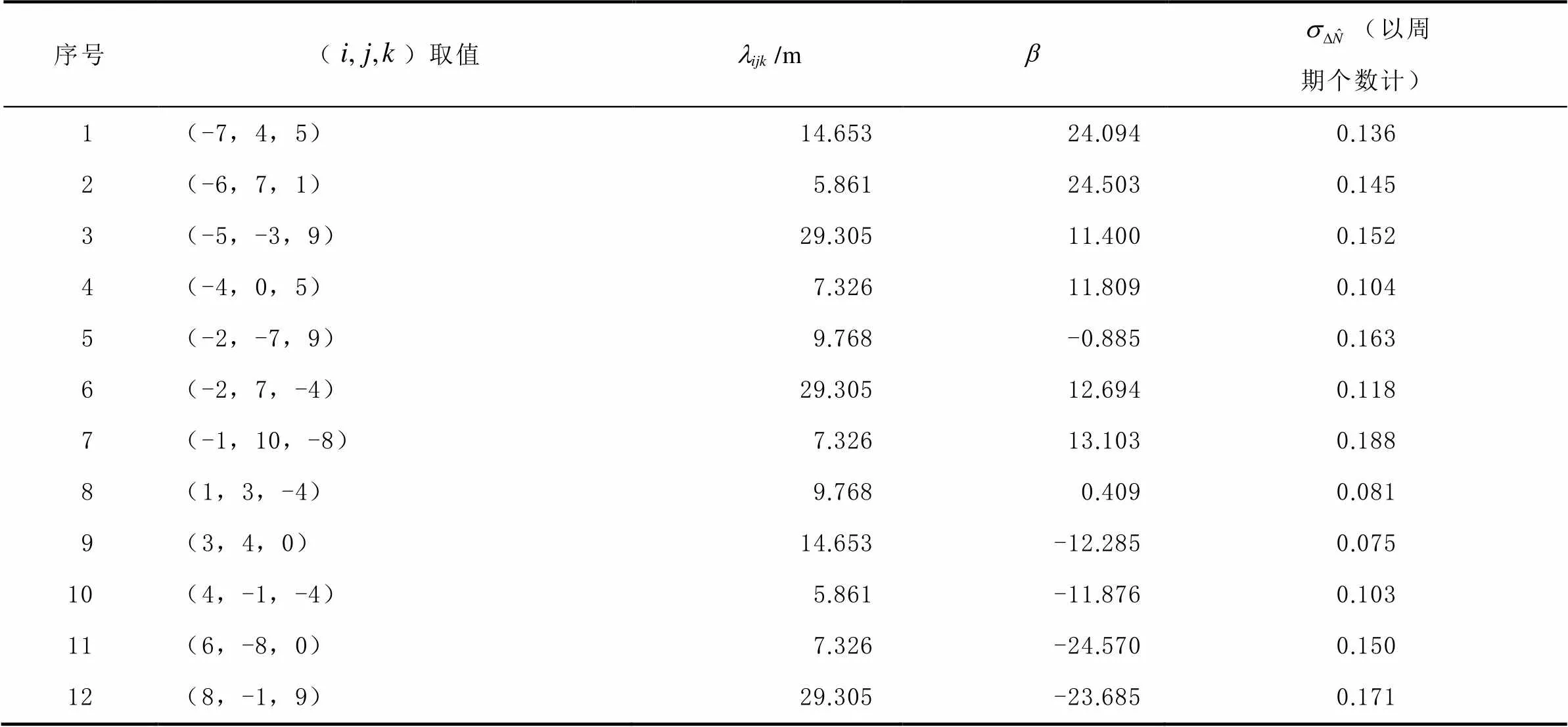
表1 满足条件的相位组合系数

根据表1和图1选择2组最优的三频相位组合系数，其中任一频率的系数不能为0；且为了避免2个伪距相位组合对3个频率上相同大小的周跳均无法探测的问题，需要有一组系数和不为零。综合考虑，组合系数（1，3，－4）和（－2，7，－4）更优，此时系数为（1，3，－4）的伪距相位组合周跳探测阈值为0.22个周期，系数为（－2，7，－4）的伪距相位组合周跳探测阈值为0.35个周期，满足整周周跳探测要求。

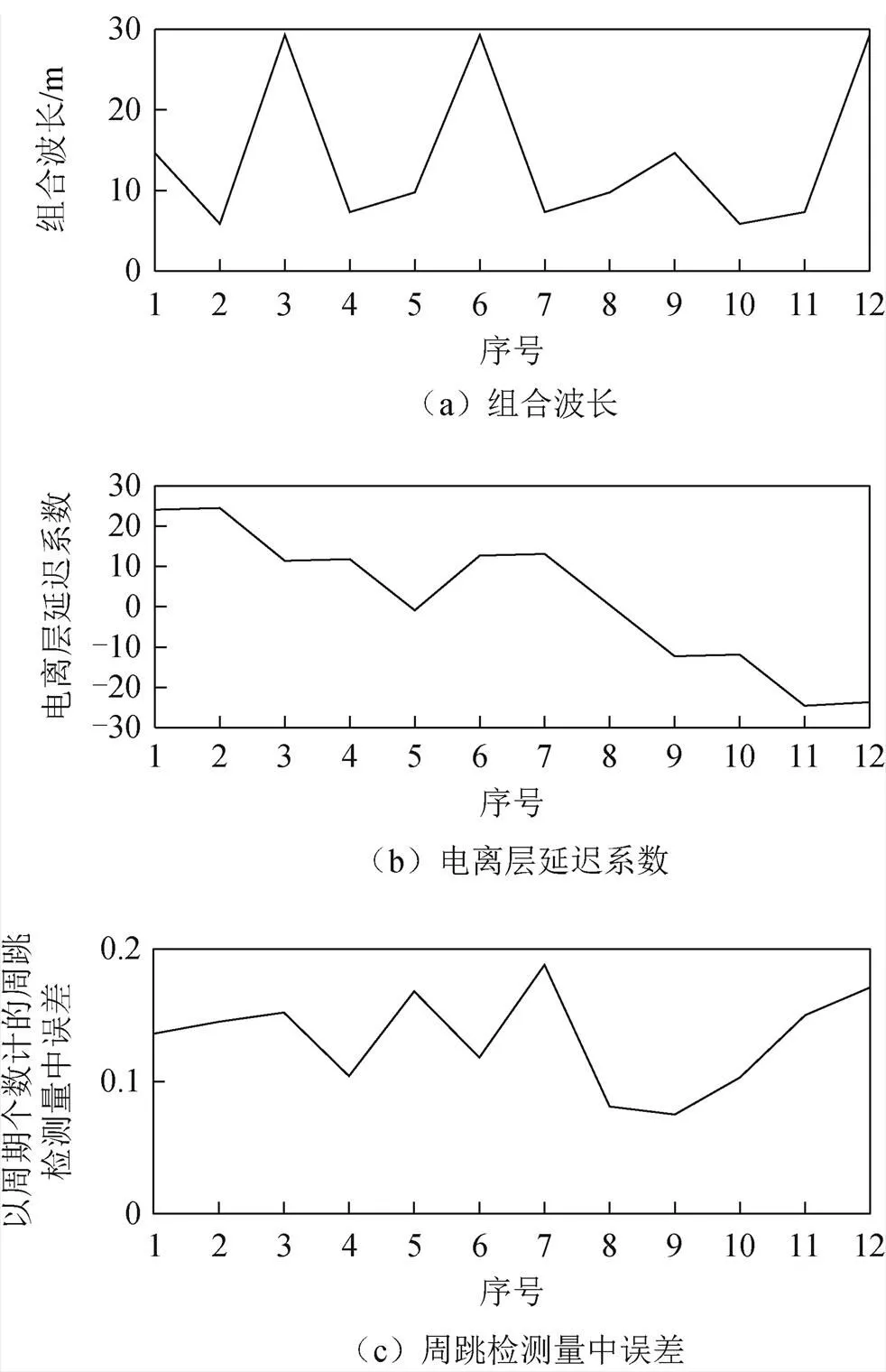
图1 各组合系数对应的条件值

1.5 组合方法周跳探测

由于多普勒积分辅助的伪距相位组合法和STPIR法都是利用三频组合观测量进行周跳探测，若要解算出单频周跳，需要构建至少3个线性无关的解算方程。本文选择2个最优的伪距相位组合和STPIR法构建方程组，其中STPIR法的组合系数为（1，1，－2），伪距相位组合1的系数为（－2，7，－4），伪距相位组合2的系数为（1，3，－4）。则三频周跳解算方程组为

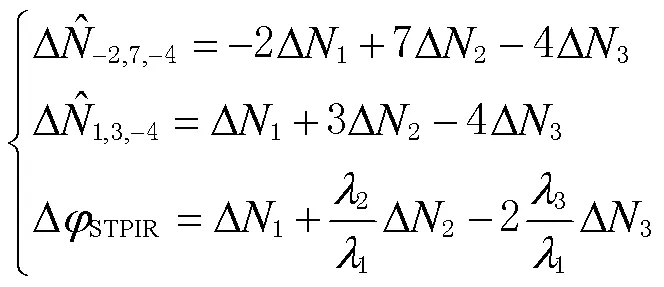
通过对方程组求解即可得到单一频率上的周跳值。

1.6 粗差判别

由于周跳和粗差的性质不同，导致二者对载波相位观测值的影响不同：周跳是从产生的历元起，以后的历元均会受到同等程度的影响；而粗差只影响当前历元的载波相位观测值，对之后的历元没有影响[22]。基于这一区别，可以判别周跳和粗差。根据2种周跳检测量的不同构造方式，具体的判断方法为：假设当前历元的任一周跳检测量超过阈值，对于伪距相位组合法，如果当前历元与后一个历元的周跳检测量大小近似相等，符号相反，与此同时，当前历元的STPIR法周跳检测量大小约为后一个历元周跳检测量的1/2，且符号相反，则认为当前历元存在粗差，否则即为周跳。为了便于计算和识别，粗差判断方法可表示为

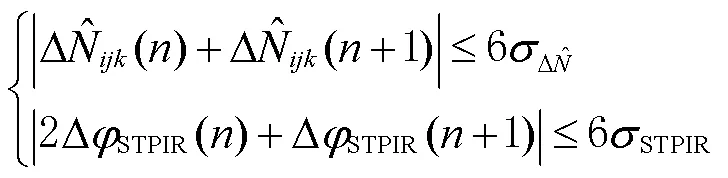
根据式（18）及周跳检测量阈值可知，理论上该方法可以分辨0.7个周期以上的周跳和粗差。

2 实验与结果分析

本文基于矩阵实验室（matrix laboratory，Matlab）软件自编程序，利用2021年3月14日辽宁某地全球卫星导航系统（global navigation satellite system，GNSS）基准站的卫星观测文件，选择北斗三号卫星导航系统（BeiDou-3 navigation satellite system，BDS-3）中卫星编号为37的三频观测数据，采样率分别为1和15 s，3个频点分别为B1c、B2a和B3。为了更好地检验本文方法的周跳探测能力，选择不含周跳的观测数据，通过人为加入不同类型的周跳值进行实验。

本次实验共分为3个：

1）实验1。对1 s采样率原始数据进行周跳探测，然后在载波相位观测值中加入不同类型的周跳并进行周跳探测，检验组合方法对小周跳、不敏感周跳以及连续周跳的探测能力。

2）实验2。首先对15 s采样率原始数据进行周跳探测，然后在载波相位观测值中加入不同大小的组合周跳，并分别利用本文的组合方法和无几何消电离层组合法进行周跳探测，对比分析周跳探测性能，检验本文提出的组合方法对较低采样率数据的周跳探测能力。

3）实验3。在15 s采样率数据中添加不同大小的周跳和粗差并进行探测，检验组合方法对周跳和粗差的判别能力。

首先进行实验1，利用组合方法对采样率为1 s的原始数据进行周跳探测，结果如图2所示。

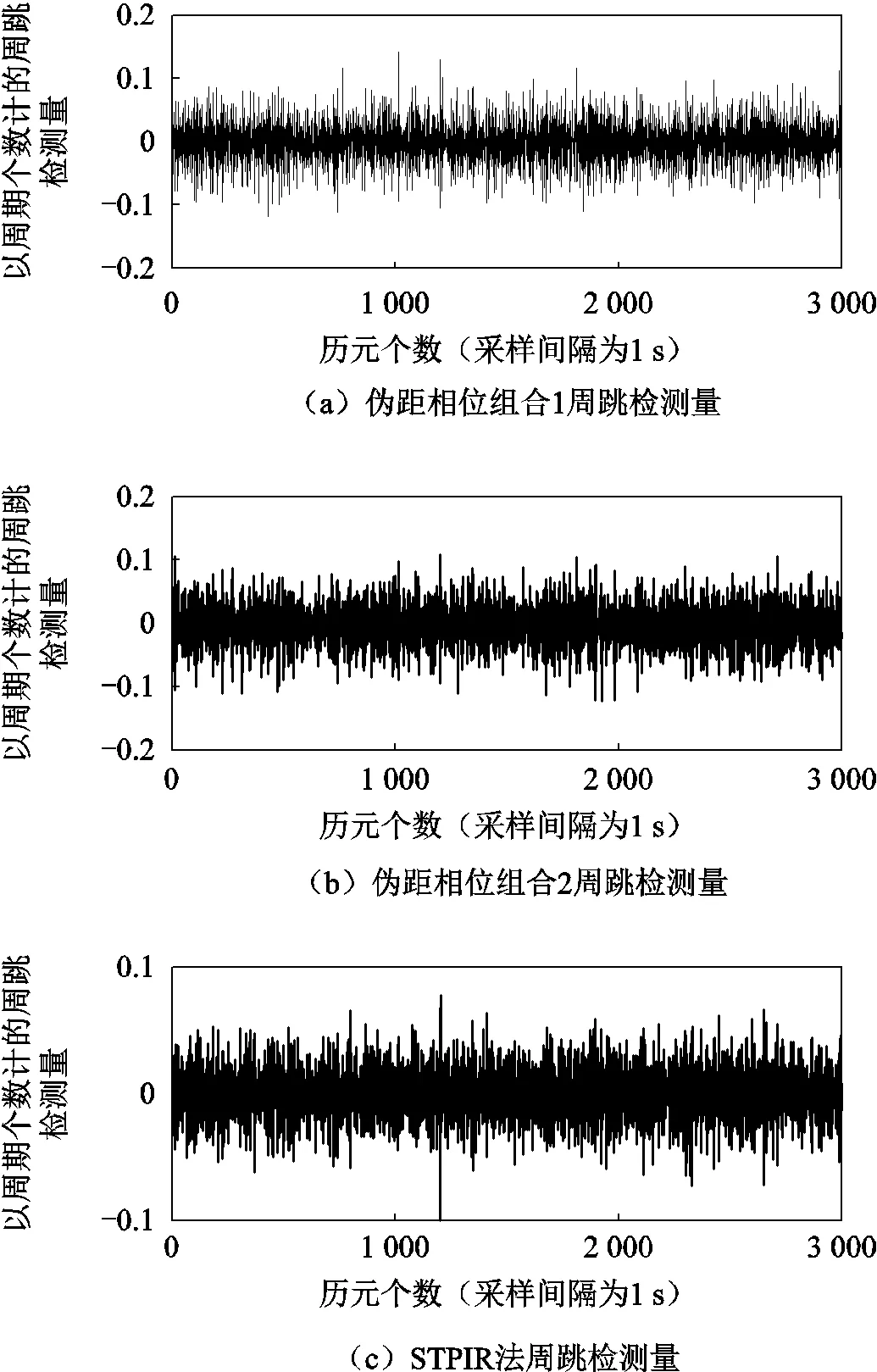
图2 1s采样率原始数据周跳检测量

从图2中可以看出：伪距相位组合1的周跳检测量小于0.14个周期，伪距相位组合2的周跳检测量大小在0.12个周期内，STPIR法周跳检测量大小控制在0.08个周期范围内；3种方法的周跳检测量均在阈值范围内，数据质量良好。

对添加周跳后的1 s采样率数据进行周跳探测，结果如图3所示。有周跳位置的周跳检测量与理论值如表2所示。

在第500个历元加入1个周期的小周跳时，3种方法均能有效探测出来，最大探测误差为 0.07个周期；在第1000个历元加入（3，4，0）个周期的组合周跳时，组合方法能准确地探测出双频周跳；在第1500个历元加入（9，10，7）个周期的组合周跳时，伪距相位组合1的周跳探测误差最大，误差值为0.009个周期，周跳探测精度良好：因此组合方法可以探测出3个频率上不同大小的周跳。

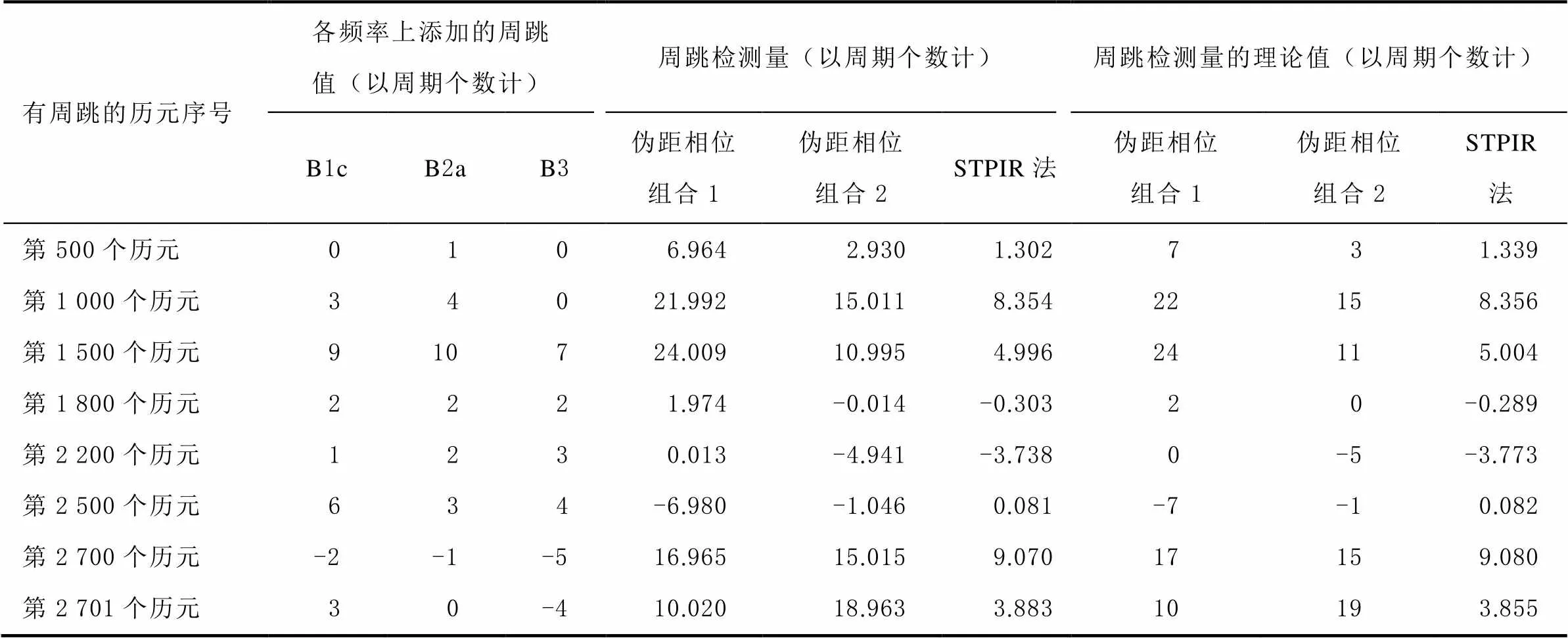
表2 1 s采样率有周跳数据的周跳探测结果

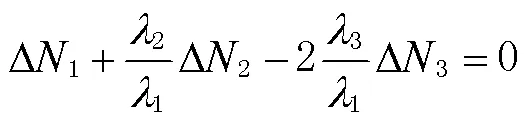
另外，在第2700、2701个历元加入了不同大小的连续周跳时，3种组合的周跳探测误差小于0.04个周期，因此组合方法对连续周跳具有良好的周跳探测能力。

综上可见，多普勒辅助的伪距相位组合法联合STPIR法弥补了各自的周跳探测盲点，可以对3个频率上不同大小的周跳、不敏感周跳及连续周跳进行探测，且周跳探测精度良好。

再按照实验2中的方法，首先对采样率为15 s的原始数据进行周跳探测，结果如图4所示。

从图4可以看出：伪距相位组合1的周跳检测量大小在0.15个周期以内，伪距相位组合2的周跳检测量大小在0.16个周期以内，STPIR法周跳检测量小于0.1个周期；3种组合的周跳检测量均在阈值范围内。

对15 s采样率数据加入周跳并利用组合方法进行周跳探测，其中有周跳位置的周跳检测量和理论值如表3所示。由于篇幅限制，因此不再配图展示周跳探测结果。同时利用无几何消电离层组合进行周跳探测实验，选择的无几何消电离层组合系数为：组合1的相位组合系数为（1，1，－2），伪距组合系数为（0.750616，0.041406，0.207978）；组合2的相位组合系数为（1，3，－4），伪距组合系数为（1.577791，－0.537279，－0.040512）；组合3的相位组合系数为（1，0，－1），伪距组合系数为（0.497328，0.358645，0.144027）。无几何消电离层组合的周跳探测结果如表4所示。

对比表3和表4可知：在15 s采样率下，本文提出的组合方法对所有周跳均能有效探测出来，尤其对小周跳的探测误差小于0.1个周期，而无几何消电离层组合对1个周期的小周跳探测误差达到0.22个周期；本文方法对不敏感周跳（6，3，4）的探测误差为0.076个周期，而无几何消电离层组合的周跳探测误差为0.148个周期，且其对3个频率上相同大小的周跳无法有效探测；另外在对第150、151个历元的连续周跳进行探测时，无几何相位组合的最大探测误差达到0.297个周期，远大于本文方法的探测误差。因此，相比无几何相位组合法，本文组合方法的周跳探测性能更优。

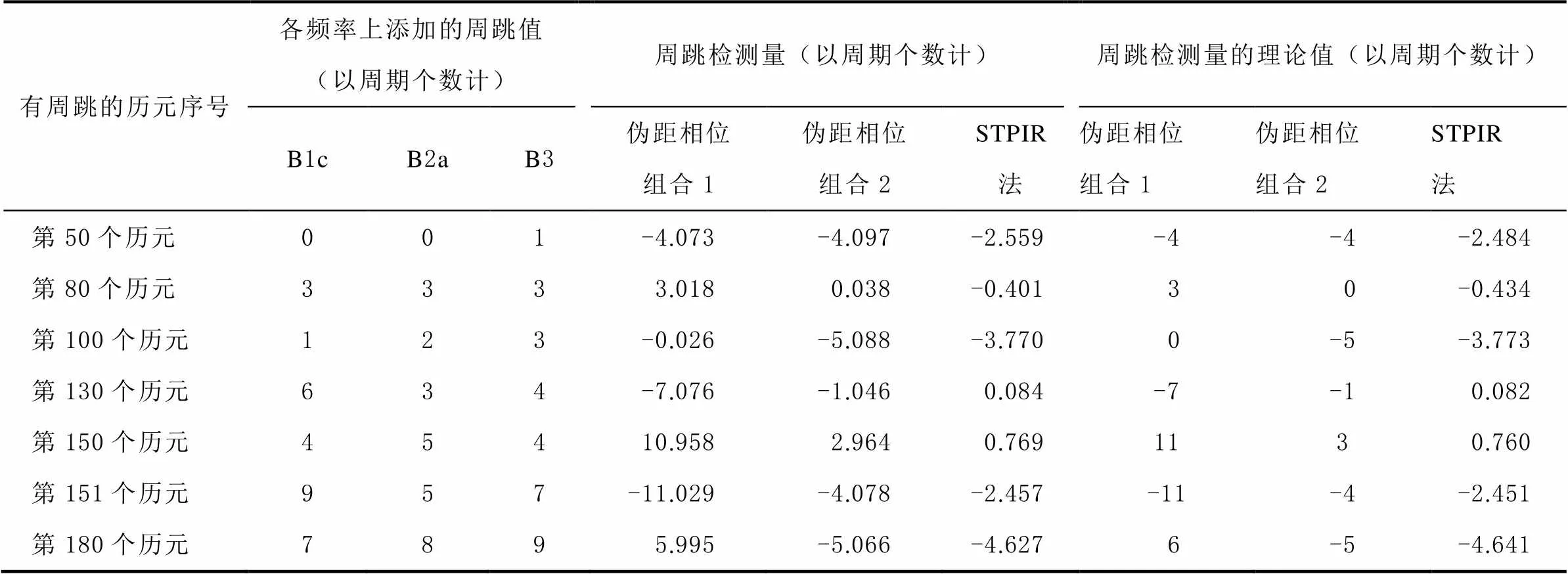
表3 15 s采样率数据组合方法周跳探测结果

最后进行实验3，在15 s采样率数据中第 50个历元处添加（0，0，1）个周期的小粗差，在第100个历元处添加（0，0，1）个周期的小周跳，在第150个历元处添加（7，0，0）个周期的较大粗差，在第180个历元处添加（6，0，0）个周期的大周跳并进行周跳探测，结果如图5所示。周跳检测量数据如表5所示，表中“—”表示周跳检测量不超过阈值。

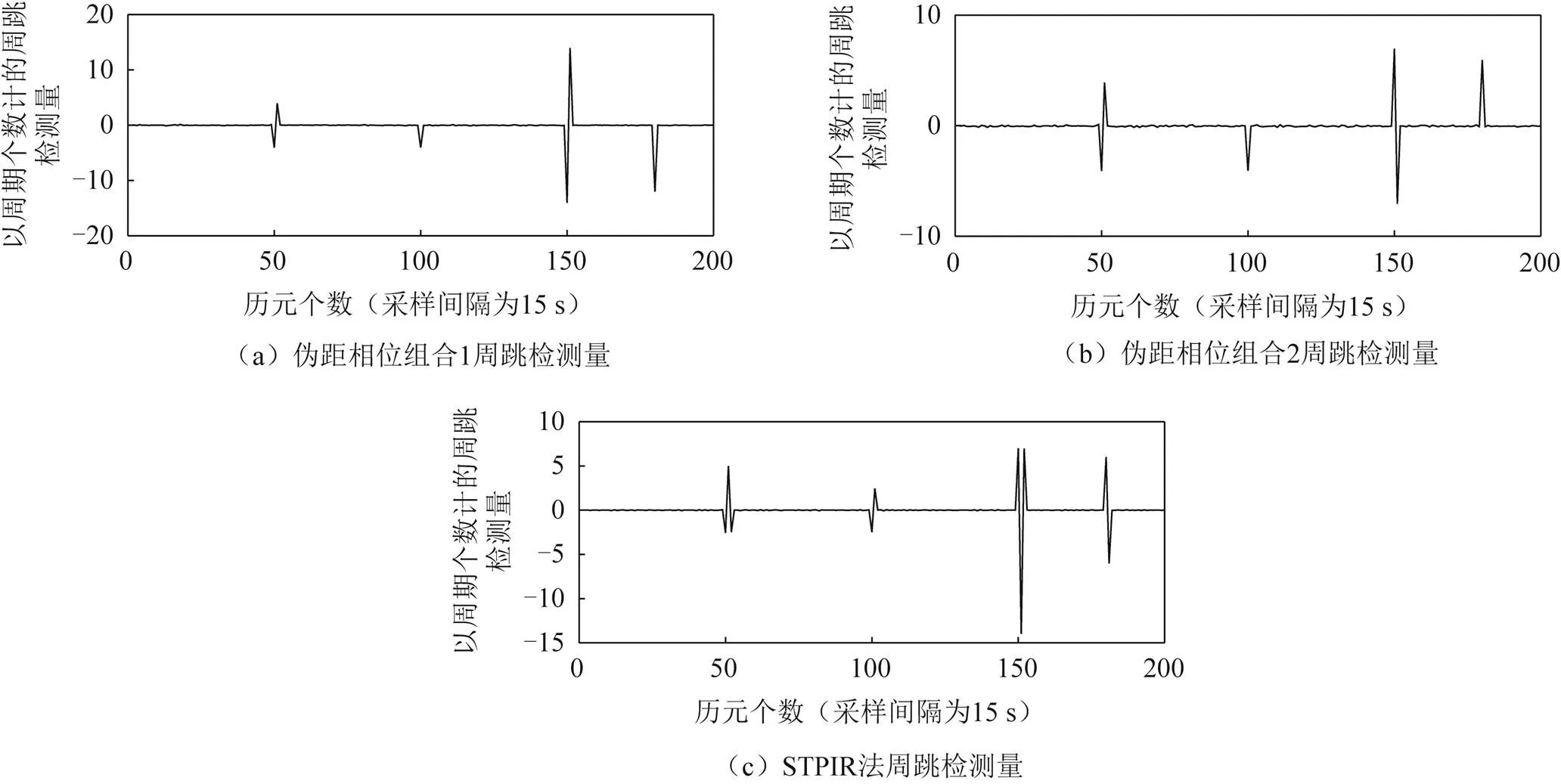
图5 加入周跳和粗差数据的周跳检测量

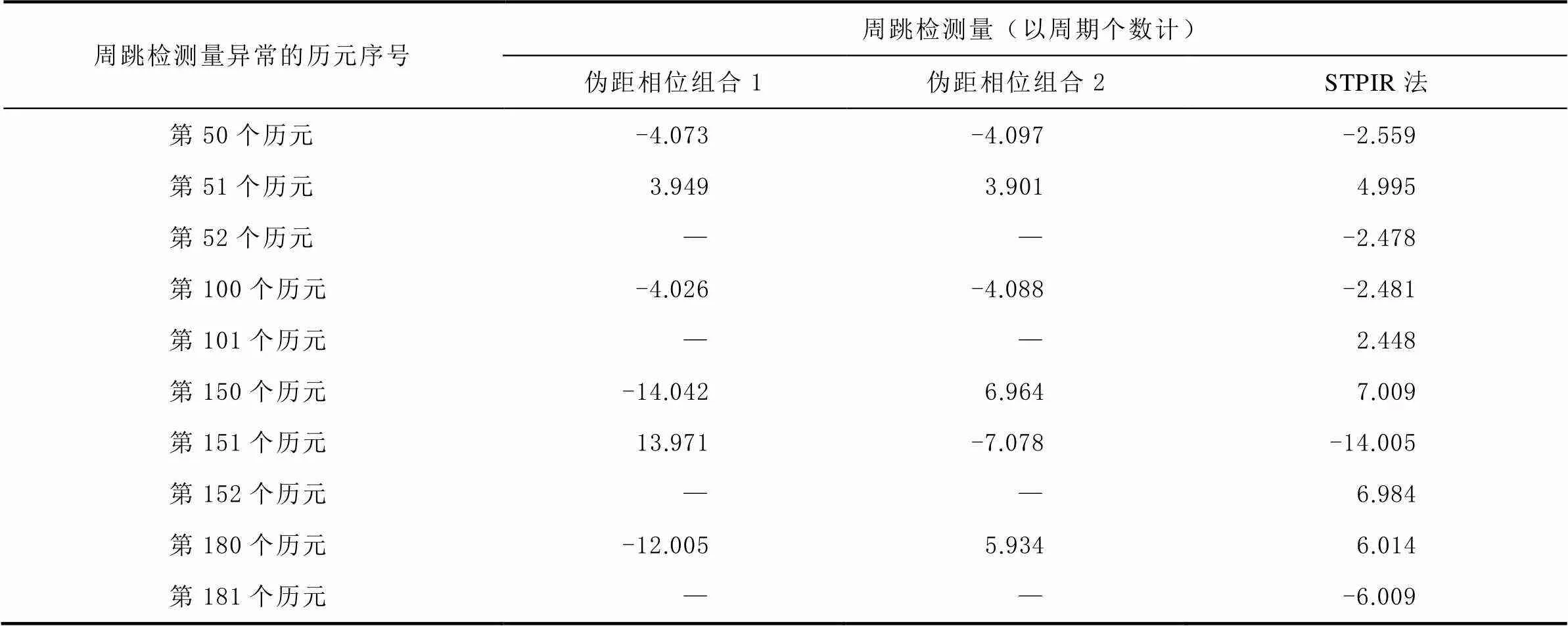
表5 加入周跳和粗差数据的探测结果

从图5可以看出：对于伪距相位组合法，周跳只影响当前历元的周跳检测量，使其超出阈值范围，而粗差则会影响当前历元和下一历元的周跳检测量；对于 STPIR法，周跳会影响当前历元和下一历元的周跳检测量出现异常，粗差则会影响当前历元和前后两个相邻历元的周跳检测量。同时利用粗差与周跳判断公式对表5中数据进行计算可知：在第50个历元加入1个周期的粗差时，伪距相位组合1在第50、51个历元的周跳检测量和为－0.124个周期；伪距相位组合2在这2个历元的周跳检测量和为－0.196个周期；而STPIR法周跳探测结果中，第50个历元周跳检测量的2倍与第51个历元周跳检测量之和为0.039个周期。这3个数值均未超出粗差的判断范围，因此可以判定为粗差而不是周跳。在第100个历元加入1个周期的周跳时，根据判断公式可以得出3个数值均超出粗差判断范围，则可以判定发生了周跳；另外，组合方法也能准确判断出第150个历元和第180个历元的较大周跳和粗差。由此可见，组合方法对1个周期以上的周跳和粗差具有良好的辨别能力。

3 结束语

本文首先选择最优的三频伪距相位组合系数构建多普勒积分辅助的伪距相位组合周跳检测量，再联合STPIR法对1和15 s采样率的BDS三频数据进行周跳探测，然后对比组合方法和无几何消电离层法的周跳探测性能，最后检验了组合方法对周跳和粗差的辨别能力，结果表明：

1）多普勒积分辅助的三频伪距相位组合法减弱了低采样率下多普勒积分误差对周跳探测的影响，提高了多普勒积分的周跳探测精度。

2）利用组合方法进行周跳探测，弥补了各自方法的周跳探测盲点，可以有效探测不同大小的三频组合周跳值，同时满足对不敏感周跳和连续周跳的探测要求。

3）组合方法可以准确地辨别1个周期以上的周跳和粗差，满足周跳探测和修复要求，为BDS高精度定位提供参考。

[1] 崔立鲁, 何琼, 邹正波, 等. 利用无几何消电离层组合实现北斗三频周跳探测与修复[J]. 测绘通报, 2020(4): 58-62.

[2] 胡辉, 陈艳, 纪兆云, 等. 基于高次差法与多项式法的GPS周跳探测与修复[J]. 河南师范大学学报(自然科学版), 2011, 39(2): 47-50.

[3] 谢世华, 肖毅峰. 基于多项式拟合的GPS周跳探测研究[J]. 资源信息与工程, 2018, 33(5): 135-136, 138.

[4] 裴晶, 马颖, 刘春. 多项式拟合法在周跳探测中的研究与改进[J]. 电子测量与仪器学报, 2017, 31(11): 1828-1834.

[5] BEZMENOV I V, BLINOV I Y, NAUMOY A V, et al. An algorithm for cycle-slip detection in a Melbourne–Wübbena combination formed of code and carrier phase GNSS measurements[J]. Measurement Techniques, 2019, 62(5): 415-421.

[6] 陈猛, 李建文, 陈星宇, 等. 联合MW组合法及改进电离层残差法的周跳探测新方法[J]. 全球定位系统, 2016, 41(4): 39-42.

[7] 沈朋礼, 成芳, 肖厦, 等. 北斗三号卫星的周跳探测与修复算法[J]. 测绘科学, 2019, 44(11): 9-14, 21.

[8] 孟令东, 陈俊平, 王解先. 小波变换联合伪距相位组合探测与修复GNSS三频周跳[J]. 测绘通报, 2020(3): 140-144.

[9] 范冬阳, 徐良. 基于伪距相位组合法和电离层残差法探测和修复周跳的研究[J]. 湘潭大学自然科学学报, 2018, 40(4): 52-55.

[10] FAN X X, TIAN R, DONG X R, et al. Cycle slip detection and repair for BeiDou-3 triple-frequency signals[J]. International Journal of Advanced Robotic Systems, 2020, 17(3).

[11] 熊旭, 崔立鲁, 钱江宇, 等. 伪距相位组合联合STPIR组合探测北斗三频周跳[J]. 北京测绘, 2019, 33(3): 291-295.

[12] 李迪, 柴洪洲, 潘宗鹏. STPIR和MW组合的北斗三频周跳探测与修复[J]. 海洋测绘, 2018, 38(1): 31-34.

[13] 杨凯淳, 吕志平, 李林阳, 等. 多普勒积分辅助的动态单频周跳探测[J/OL]. 武汉大学学报(信息科学版) . (2021-11-05)[2022-08-08].https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename= WHCH20211104007&uniplatform=NZKPT&v=kv866gsLbeNEbegCkAWDycvB58Eu8xtT11fFfWpBkdNXiaPrz_1JKY1pQRqIA7qK.

[14] 蔡成林, 沈文波, 曾武陵, 等. 多普勒积分重构与STPIR联合周跳探测与修复[J]. 测绘学报, 2021, 50(2): 160-168.

[15] 邰贺, 张小红, 张明, 等. GPS单频精密单点定位方法与实践[J]. 测绘信息与工程, 2008(3): 1-3.

[16] 刘俊, 何秀凤, 刘炎雄. 北斗三频非差观测数据的周跳探测与修复方法[J]. 大地测量与地球动力学, 2014, 34(4): 117-122.

[17] 王建敏, 马天明, 祝会忠. 改进LAMBDA算法实现BDS双频整周模糊度快速解算[J]. 系统工程理论与实践, 2017, 37(3): 768-772.

[18] 祝会忠, 雷啸挺, 李军, 等. BDS参考站三频整周模糊度单历元确定方法[J]. 测绘学报, 2020, 49(11): 1388-1398.

[19] 祝会忠, 雷啸挺, 徐爱功, 等. 顾及GEO卫星约束的长距离BDS三频整周模糊度解算[J]. 测绘学报, 2020, 49(9): 1222-1234.

[20] 付伟, 帅玮祎, 董绪荣. 基于北斗三号三频数据的周跳探测与修复[J]. 测绘工程, 2020, 29(2): 30-35.

[21] 崔立鲁, 杜石. 北斗三频无几何相位组合实时周跳探测与修复[J]. 科学技术与工程, 2018, 18(29): 7-12.

[22] 王帅, 高井祥. 利用三频组合观测值进行GPS周跳探测与修复[J]. 测绘科学, 2012, 37(5): 40-42.

Doppler integration assisted BDS triple frequency cycle slip detection

WANG Jianmin, WANG Qingwang, HUANG Jiapeng

（School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China）

Aiming at the problem of low cycle slip detection accuracy for low sampling rate data by single frequency Doppler integral, the paper proposed a cycle slip detection method for Doppler integral assisted pseudorange phase combination based on the three frequency observation data of BeiDou navigation satellite system (BDS): Doppler integration was used to calculate the variation of pseudorange between epochs for greatly reducing the influence of multipath effects; and the combined cycle slip detection quantity of wide lane phase and narrow lane pseudorange was constructed by selecting the optimal three frequency combination coefficients, to improve the cycle slip detection accuracy of Doppler integration for low sampling rate data. Experimental result showed that the proposed combined method would make up for the blind spots of each cycle slip detection; and for data with different sampling rates, it could not only effectively detect and repair large and small cycle slips, continuous cycle slips and insensitive cycle slips, but also accurately identify cycle slips and gross errors of more than one cycle, indicating good cycle slip detection performance.

cycle slip detection; BeiDou navigation satellite system (BDS); Doppler integration; pseudorange phase combination

王建敏, 王清旺, 黄佳鹏. 多普勒积分辅助BDS三频周跳探测[J]. 导航定位学报, 2023, 11(3): 80-90.（WANG Jianmin, WANG Qingwang, HUANG Jiapeng. Doppler integration assisted BDS triple frequency cycle slip detection[J]. Journal of Navigation and Positioning, 2023, 11(3): 80-90.）

10.16547/j.cnki.10-1096.20230311.

P228

A

2095-4999(2023)03-0080-11

2022-05-10

国家自然科学基金项目（41474020）。

王建敏（1973—），男，甘肃酒泉人，硕士，副教授，研究方向为空间大地测量数据处理和变形监测。

王清旺（1997—），男，河南南阳人，硕士研究生，研究方向为GNSS数据处理。