不同电离层改正的PPP时间传递性能评估

郭敬雨，左鸿铭，龚晓鹏，郭文飞，辜声峰，赵齐乐

不同电离层改正的PPP时间传递性能评估

郭敬雨，左鸿铭，龚晓鹏，郭文飞，辜声峰，赵齐乐

（武汉大学 卫星导航定位技术研究中心，武汉 430079）

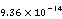
精密单点定位（PPP）；单向授时；时间传递；区域电离层格网图（RIM）；阿伦方差

0 引言

高精度时间传递是时间实验室建立和维持标准时间尺度和时间同步的基础。随着空间技术的发展，时间传递精度不断提高。文献[1]提出了全球定位系统（global positioning system，GPS）卫星共视（common view，CV）时间传递技术。文献[2]提出了GPS卫星全视（all in view，AV）时间传递技术，并指出其比CV具有更远的时间传递距离和更好的性能。然而，GPS CV和GPS AV均采用伪距观测值，受伪距观测噪声影响，精度只能达到纳秒水平。近年来基于精密单点定位（precise point positioning，PPP）的时间传递方法在精度和覆盖范围方面表现出优越的性能，使其成为全球卫星导航系统（global navigation satellite system，GNSS）时间传递最常用方法之一，并于2009年应用于国际原子时（international atomic time，TAI）服务[3-5]。文献[6]开展了基于GPS的PPP时间传递研究，结果表明静态模式下PPP时间传递精度为0.3 ns。

传统PPP时间传递模型通常基于无电离层PPP（ionosphere-free PPP，IF-PPP）展开，随着多频率多系统数据处理技术的发展，非差非组合PPP（undifferenced and uncombined PPP，UDUC-PPP）模型成为GNSS数据处理研究热点[7]。文献[8]对非组合PPP精密授时的性能进行了研究分析，结果表明非差非组合PPP算法授时精度优于传统PPP算法。文献[9]分析了以电离层延迟为参数、以全球电离层格网图（global ionosphere map，GIM）获得的电离层延迟为约束的单频PPP时间传递精度，并指出在截止高程角为10°、20°和30°时，电离层约束模型时间传递的标准差（standard deviation，STD）均能达到0.5 ns水平。值得注意的是，电离层延迟参数的处理策略显著影响非差非组合模型解算性能[10-11]，进而影响PPP时间传递性能。文献[12]提出了GNSS电离层参数化模型（deterministic plus stochastic ionospheric delay modeling for GNSS，DESIGN），该模型中电离层参数化同时顾及电离层确定性与随机性，并将先验电离层模型作为虚拟观测值，提升了非差非组合PPP定位性能[13-14]；然而其在时间传递中的应用性能还有待进一步分析。

为验证DESIGN参数化模型，及不同精度电离层改正产品在非差非组合PPP时间传递中的应用效果，本文基于欧洲区域观测网进行实验。首先给出PPP单向授时及时间传递技术的基本原理，重点对比无电离层组合PPP与非差非组合PPP的区别；然后，基于5个外接氢原子钟（hydrogen maser，H-MASER）的GNSS观测站连续21 d的数据，分析不同PPP模型的时间传递性能。

1 PPP单向授时及时间传递原理

GNSS PPP单向授时使用载波相位和伪距观测值，结合国际GNSS服务组织（International GNSS Service，IGS）提供的高精度卫星轨道和钟差等产品，由用户通过PPP方式解算出本地接收机钟差。由于IGS钟差文件对应的是IGS时间基准（IGS time，IGST）[15]，因此通过改正本地接收机钟差，即可使得本地时间与IGST同步。GNSS伪距和载波相位的非差非组合观测量[16]一般表示为

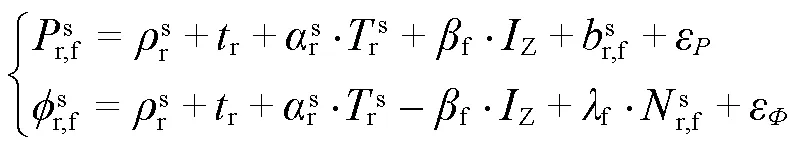
1.1 无电离层组合PPP模型

IF-PPP模型将不同频率的伪距和相位观测值通过线性组合消除电离层延迟一阶项[13]，即

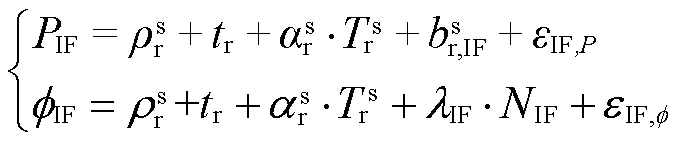
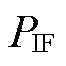
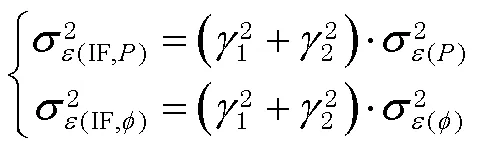
伪距观测中的电离层硬件延迟将被接收机钟差通过无电离层组合充分吸收，即

1.2 非差非组合PPP模型

UCUD-PPP模型基本观测模型即由式（1）表示，同时进一步引入DESIGN模型实现电离层参数化估计[12,14]，即

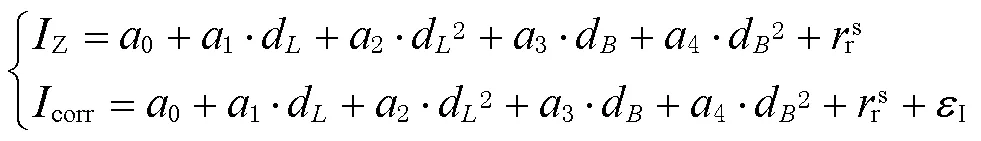
此外，为了消除接收机钟差和码偏差的线性相关性，将其合并为

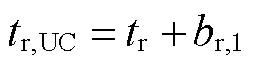
将式（4）和式（5）代入式（1），则基于DESIGN的非差非组合PPP模型为

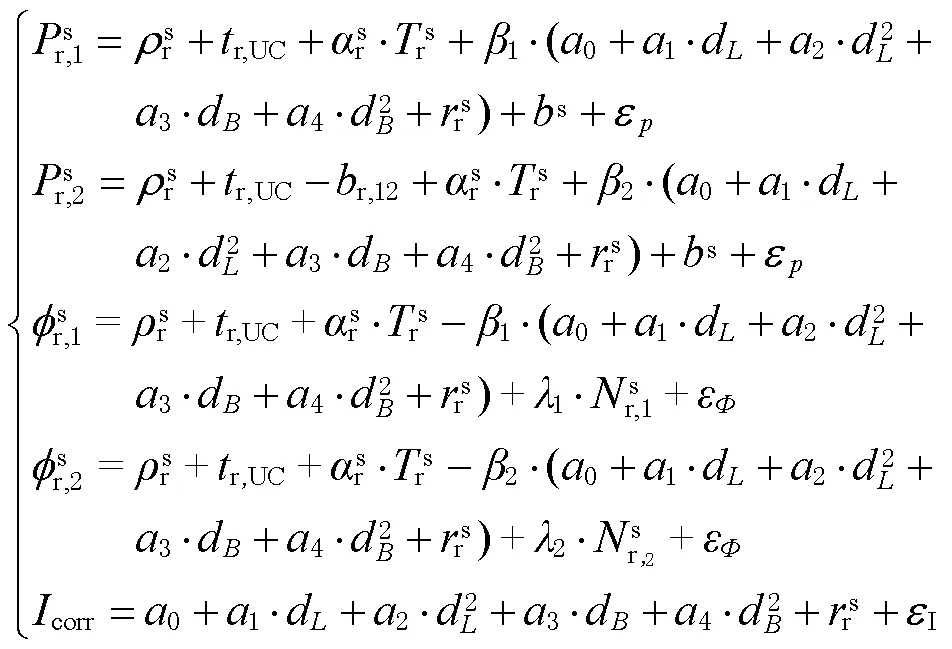
比较式（4）和式（6），可得到IF-PPP与UCUD-PPP模型的接收机钟差关系为

1.3 PPP时间传递估计噪声评估

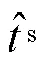
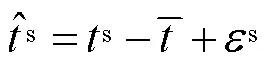
则PPP中估计的接收机钟差可表示为

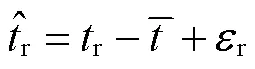
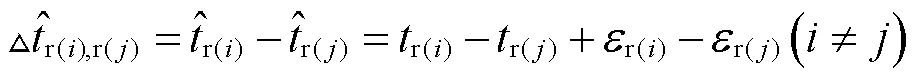
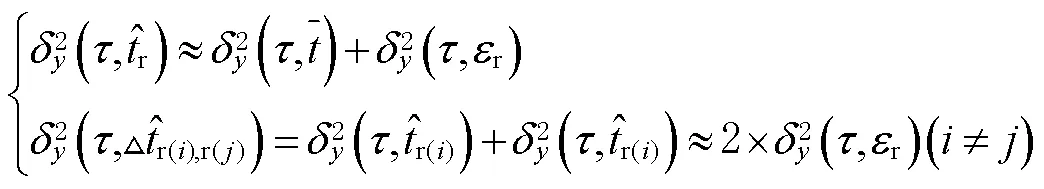
2 实验与结果分析

为验证无电离层组合与非差非组合对PPP时间传递服务性能的影响，我们基于复兴软件（fusing in GNSS，FUSING）实现了上述IF-PPP、UCUD-PPP时间传递算法。此外，本文不仅分析了GIM改正模型，也采用FUSING软件构建了区域电离层模型（regional ionosphere map，RIM），对比了二者在非差非组合PPP时间传递中的应用效果。目前，FUSING能够实现实时GNSS多系统精密定轨（precise orbit determination，POD）[21]、卫星钟差估计[22-23]、信号偏差解算[22,24]、多传感器导航[24]和大气建模[25]。

2.1 数据及策略

由式（10）可知，为准确评估不同PPP模型时间传递噪声，本地时钟应尽可能稳定。因此本文实验采用欧洲永久观测网（Euref permanent network，EPN）的BRUX、IENG、PTBB、SPT0和WAB2共5个跟踪站数据，此外选择了202个站用于区域电离层建模RIM[26]。5个跟踪站的详细信息如表1所示，这些站均参与了国际计量局（Bureau International des Poids et Mesures，BIPM）的TAI维护，并配备了外接H-MASER。表1中：ORB（Observatoire Royal de Belgique）为比利时皇家天文台；IT（Istituto Nazionale di Ricerca Metrologica）为意大利国家计量研究所；PTB（Physikalisch-Technische Bundesanstalt）为德国物理技术联邦研究院；RISE（Research Institutes of Sweden AB）为瑞典国家研究院；METAS（Federal Institute of Metrology）为瑞士联邦计量科学研究院。

表1 测站信息

表2列出了PPP处理策略。表中：GPTS（GPS time）为GPS时间；GPT2（global pressure and temperature 2）为全球气温气压模型；PCO（phase center offset）为天线相位中心偏差；PCV（phase center variation）为天线相位中心变化。实验时段为2020年年积日（day of year，DOY）第11—31天，观测值采样间隔为30 s。轨道和钟差选取IGS最终精密产品。此外，本文区域电离层建模以及PPP时间传递均采用前向平方根信息滤波器实现。

表2 PPP处理策略

2.2 区域电离层产品精度

如图1所示，以BRUX测站2020年年积日第11天为例，固定测站坐标，反算电离层延迟作为参考值，并将其与RIM内插得到的电离层延迟作差，获得其差值时间序列。如图2所示，GPS卫星的电离层延迟差值大部分小于0.2 m。图2给出了BRUX、IENG、PTBB、SPT0和WAB25个测站的GPS卫星G01至G32连续21 d的电离层延迟差值均方根统计值（root mean square，RMS）的均值，作为RIM模型的精度评估指标。除测站SPT0部分卫星外，其余卫星的天顶电离层延迟精度均优于0.14 m，其平均精度分别为0.05、0.06、0.07、0.08、0.05 m，显著优于GIM模型标称精度。

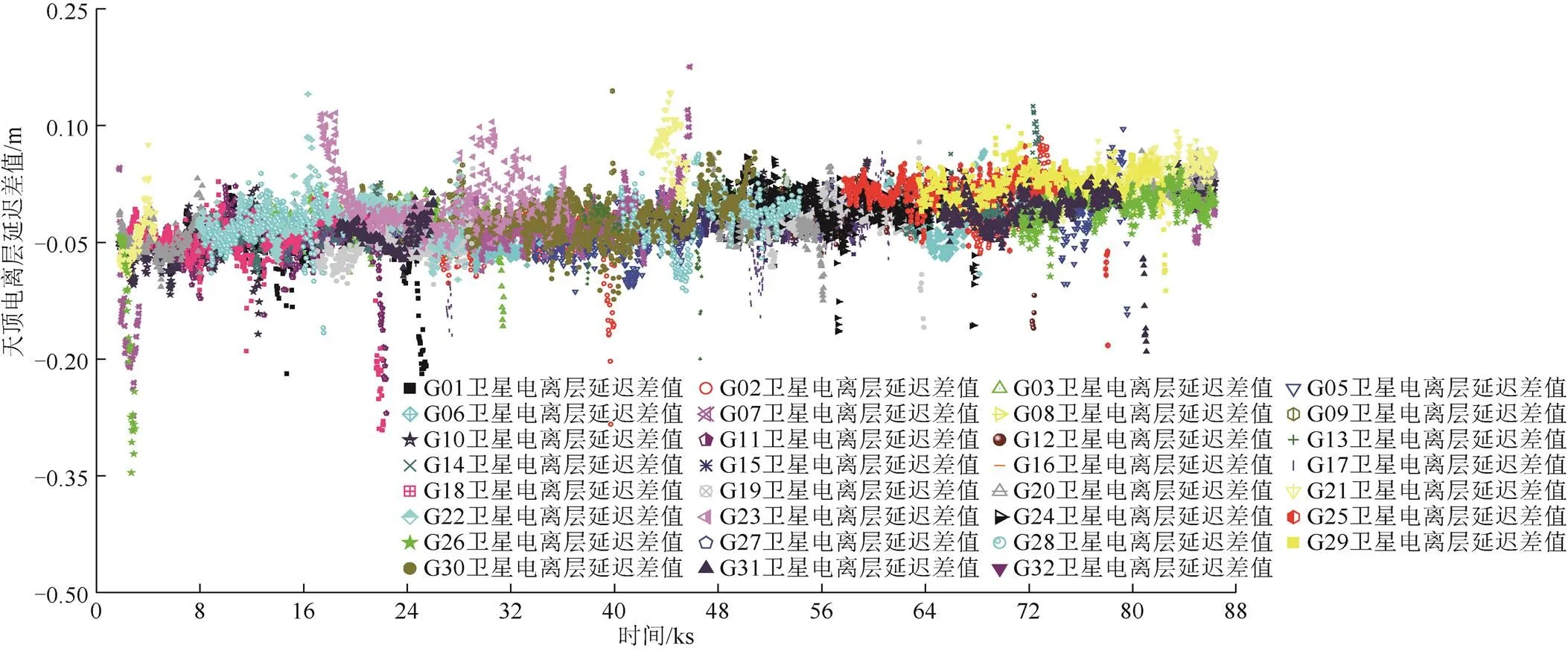
图1 BRUX测站L1信号区域电离层产品与后处理模式下反算天顶电离层延迟差值时间序列（2020，DOY 011）

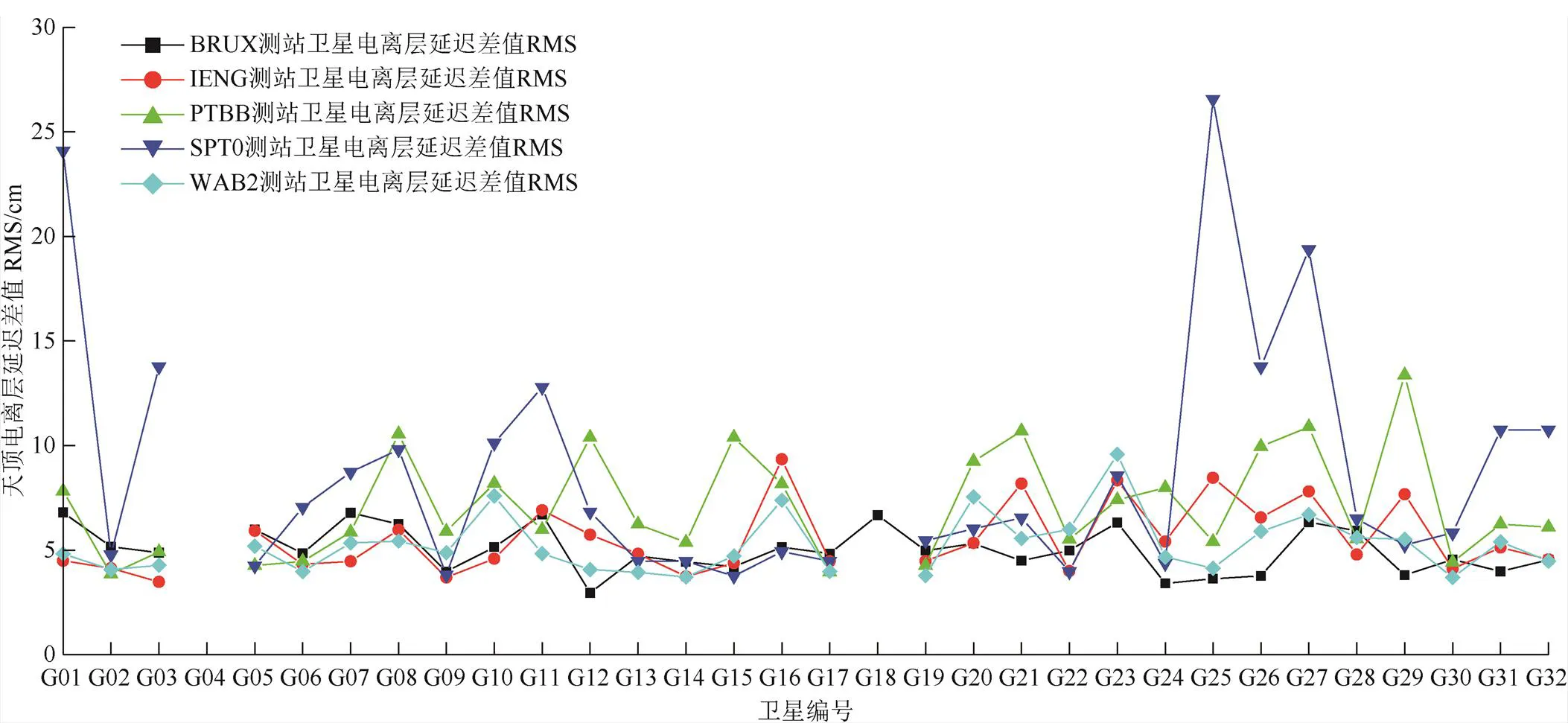
图2 5个测站L1信号区域电离层产品与后处理模式下反算天顶电离层延迟差值的RMS统计值

2.3 PPP单向授时性能评估

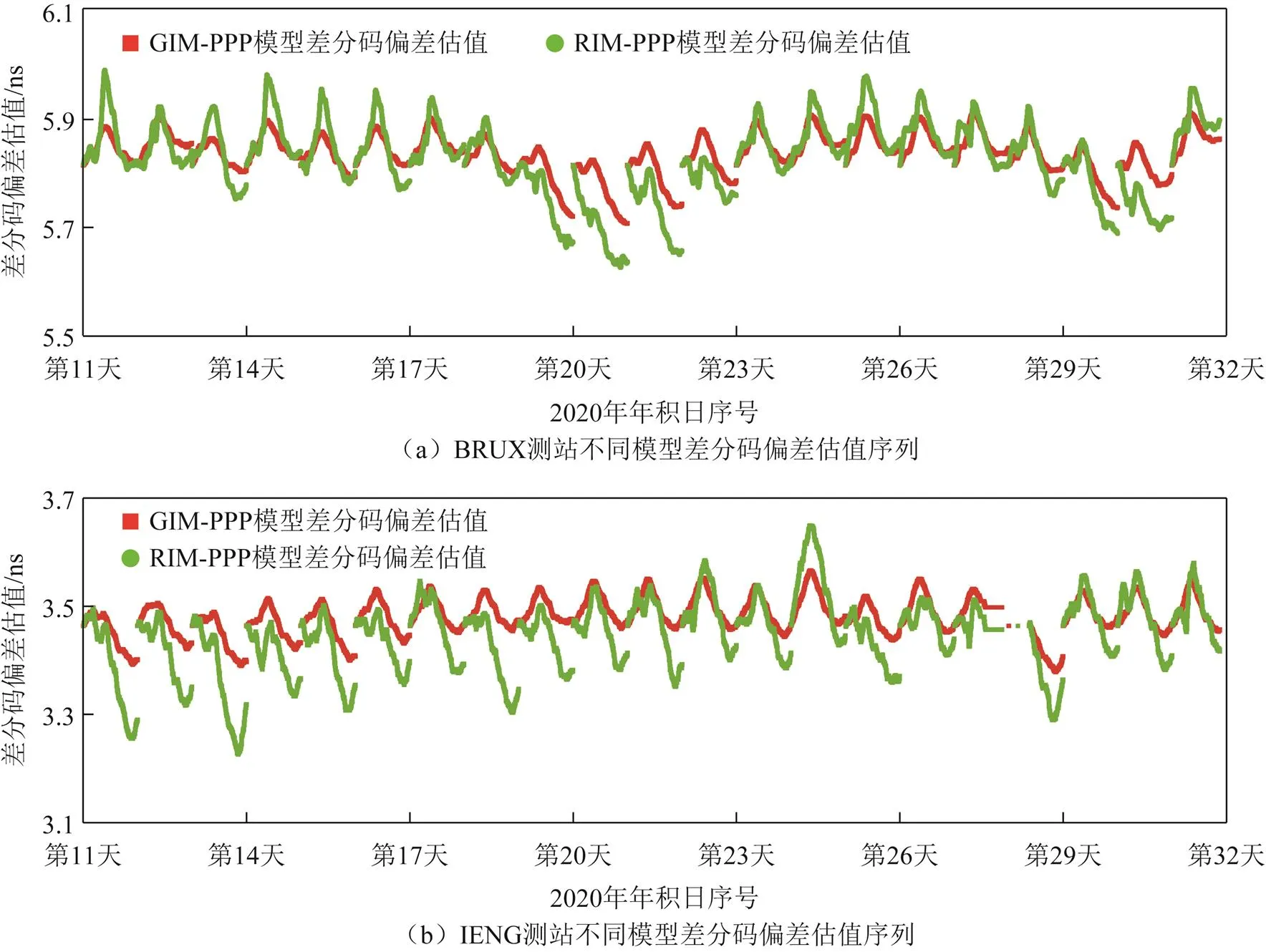
由式（6）可知，IF-PPP与UCUD-PPP解算获得的接收机钟差受DCB影响。为此，图3给出了全球基于全球电离层格网图的非差非组合PPP（global ionosphere map PPP，GIM-PPP）和基于区域电离层格网图的非差非组合PPP（regional ionosphere map PPP，RIM-PPP）解算获得的DCB序列，其中：GIM-PPP解算的DCB波动较小，这主要是由电离层延迟与DCB强相关；而GIM-PPP相对于RIM-PPP电离层模型精度较低，其对电离层延迟参数施加的约束较弱，同时DCB作为单天常数估计，因此GIM-PPP解算的DCB时域上更稳定。此外，GIM-PPP与RIM-PPP中DCB单天平均稳定性STD分别为0.023和0.052 ns，都明显高于PPP钟差解算稳定性；因此可以认为其对PPP单向授时及时间传递噪声稳定性评估影响较小。

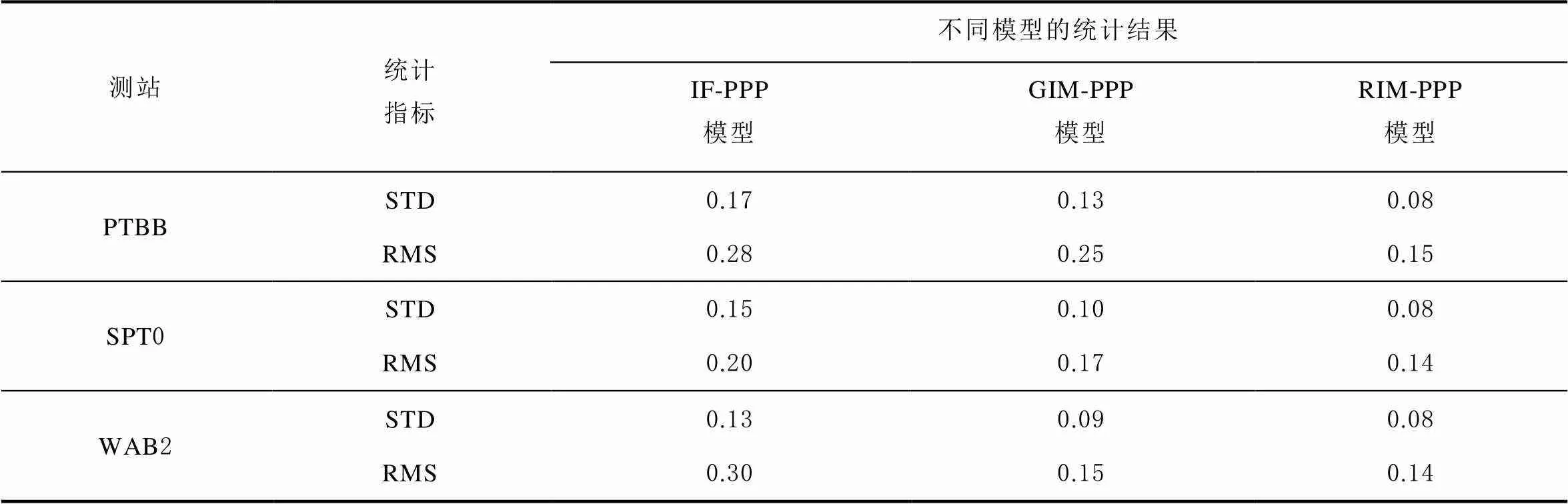
目前IGS提供的事后跟踪站钟差以IGST为基准，标称精度RMS为75 ps[27]，可将其作为参考真值进行对比。表3给出了以IGS最终精密钟差文件中测站接收机钟差产品为参考，连续21 d的IF-PPP、GIM-PPP和RIM-PPP模型单向授时的标准差和均方根统计值。从表3中可以看出：GIM-PPP和RIM-PPP模型钟差解算精度均优于IF-PPP模型；BRUX、IENG、PTBB、SPT0、WAB25个测站的单向授时RMS分别提高了21%、25%、10%、17%、49%和47%、47%、45%、29%、51%；2种模型的RMS相对IF-PPP平均分别提升了24%和44%。

（续）

2.4 时频传递性能评估

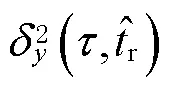
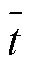
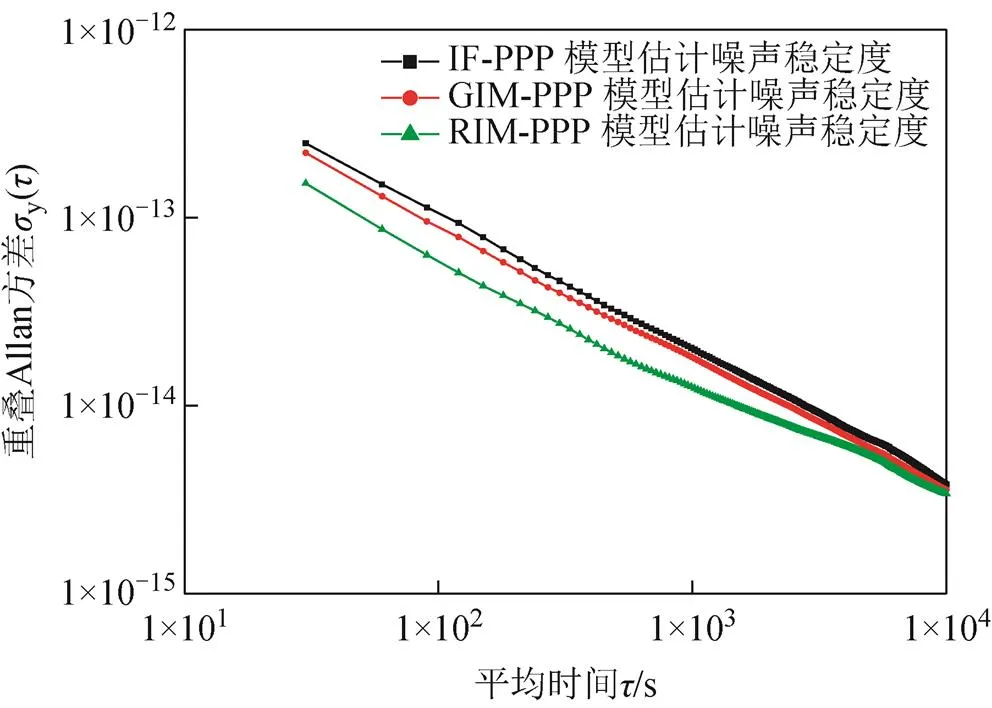
图5 IF-PPP、GIM-PPP和RIM-PPP模型的PPP估计噪声重叠Allan方差

3 结束语

本文对比分析了无电离层组合PPP和非差非组合PPP时间传递模型，给出了二者接收机钟差参数转换关系。在此基础上，结合2020年年积日第11—31天EPN跟踪站数据，采用重叠Allan方差等指标评估了IF-PPP及不同电离层改正的UCUD-PPP时间传递性能。

实验结果表明，基于全球电离层格网图的非差非组合PPP相比IF-PPP在单向授时精度及时间传递稳定性方面具有明显优势，当采用202个EPN站构建的区域电离层模型增强非差非组合PPP时，其性能进一步提升。相较于IF-PPP模型，GIM-PPP和RIM-PPP模型单向授时的精度平均分别提高24%和44%。在时间传递稳定度方面，与传统IF-PPP模型相比，GIM-PPP和RIM-PPP模型在短期项稳定度上表现出明显的改善。RIM-PPP模型的短期项稳定度明显提高，提高了约45%。

[1] ALLAN D W, WEISS M A. Accurate time and frequency transfer during common-view of a GPS satellite[C]// The Institute of Electrical and Electronic Engineers (IEEE). Proceedomgs of the 34th Annual Symposium on Frequency Control. Philadelphia: IEEE, 1980: 334-346[2022-07-26].

[2] JIANG Z. Time transfer with GPS satellites all in view[C]// The Technical Committee of Time and Frequency (APMP). Proceedomgs of Asia Pacific Workshop on Time and Frequency. Beijing: APMP, 2004: 236-243[2022-07-26].

[3] PETIT G. The TAIPPP pilot experiment[C]// The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of International Frequency Control Symposium Joint with the 22nd European Frequency and Time forum. Besancon: IEEE, 2009: 116-119[2022-07-26].

[4] PETIT G, JIANG Z. Precise point positioning for TAI computation[C]// The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum. Geneva: IEEE, 2007: 395-398[2022-07-26].

[5] YAO J, SKAKU I, JIANG Z, et al. A detailed comparison of two continuous GPS carrier-phase time transfer techniques[J]. Metrologia, 2015, 52(5): 666-676.

[6] PETIT G, HARMEGNIES A, MERCIER F, et al. The time stability of PPP links for TAI[C]// The Institute of Electrical and Electronic Engineers (IEEE). Proceedings of Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings. San Francisco: IEEE, 2011: 1-5[2022-07-26].

[7] ZHOU F, DONG D, LI W, et al. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations[J]. GPS Solutions, 2018, 22(2):1-10.

[8] 闫伟, 袁运斌, 欧吉坤, 等. 非组合精密单点定位算法精密授时的可行性研究[J]. 武汉大学学报(信息科学版), 2011, 36(6): 648-651.

[9] GE Y L, ZHOU F, DAI P, et al. Precise point positioning time transfer with multi-GNSS single-frequency observations[J]. Measurement, 2019, 146: 628-642.

[10] ROSE J A R, WATSON R J, ALLAIN D J, et al. Ionospheric corrections for GPS time transfer[J]. Radio Science, 2014, 49(3): 196-206.

[11] SU K, JIN S, HOQUE M M. Evaluation of ionospheric delay effects on multi-GNSS positioning performance[J]. Remote Sensing, 2019, 11(2):171.

[12] SHI C, GU S F, LOU Y D, et al. An improved approach to model ionospheric delays for single-frequency precise point positioning[J]. Advance in Space Research, 2012, 49(12): 1698-1708.

[13] ZHAO Q L, WANG Y T, GU S F, et al. Refining ionospheric delay modeling for undifferenced and uncombined GNSS data processing[J]. Journal of Geodesy, 2019, 93(4): 545-560.

[14] LOU Y D, ZHENG F, GU S F, et al. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models[J]. GPS Solutions, 2016, 20(4): 849-862.

[15] SENIOR K L, RAY J R, BEARD R L. Characterization of periodic variations in the GPS satellite clocks[J]. GPS Solutions, 2008, 12(3): 211-225.

[16] LEICK A, RAPOPORT L, TATARNIKOV D. GPS satellite surveying[M]. San Francisco: John Wiley & Sons, 2015: 404-405.

[17] LI X, ZHANG X, GE M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution[J]. Journal of Geodesy, 2011, 85(3): 151-158.

[18] KOUBA J. A guide to using International GNSS Service (IGS) products[EB/OL]. (2009-05-01)[2022-07-26]. http://acc.igs.org/UsingIGSProductsVer21.pdf.

[19] YANG X H, GU S F, GONG X P, et al. Regional BDS satellite clock estimation with triple-frequency ambiguity resolution based on undifferenced observation[J]. GPS Solutions, 2019, 23(2): 1-11.

[20] GUO W F, ZUO H M, MAO F Y, et al. On the satellite clock datum stability of RT-PPP product and its application in one-way timing and time synchronization[J]. Journal of Geodesy, 2022, 96(8): 1-14.

[21] LOU Y D, DAI X L, GONG X P, et al. A review of real-time multi-GNSS precise orbit determination based on the filter method[J]. Satellite Navigation, 2022, 3(1): 1-15.

[22] GONG X P, GU S F, LOU Y D, et al. An efficient solution of real-time data processing for multi-GNSS network[J]. Journal of Geodesy, 2018, 92(7): 797-809.

[23] SHI C, GUO S, GU S F, et al. Multi-GNSS satellite clock estimation constrained with oscillator noise model in the existence of data discontinuity[J]. Journal of Geodesy, 2019, 93(4): 515-528.

[24] GU S F, DAI C Q, FANG W, et al. Multi-GNSS PPP/INS tightly coupled integration with atmospheric augmentation and its application in urban vehicle navigation[J]. Journal of Geodesy, 2021, 95(6): 64.

[25] LUO X, GU S F, LOU Y D, et al. Amplitude scintillation index derived from C/N0 measurements released by common geodetic GNSS receivers operating at 1 Hz[J]. Journal of Geodesy, 2020, 94(2): 27.

[26] SONG W W, HE C P, Gu S F. Performance analysis of ionospheric enhanced PPP-RTK in different latitudes[J]. Geomatics and Information Science of Wuhan University, 2021, 46(12): 1832-1842.

[27] 李征航, 黄劲松. GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2010: 95-96.

Performance evaluation of PPP time transfer by different ionospheric correction strategies

GUO Jingyu, ZUO Hongming, GONG Xiaopeng, GUO Wenfei, GU Shengfeng, ZHAO Qile

（Research Center of GNSS, Wuhan University, Wuhan 430079, China）

precise point positioning (PPP); one-way timing; time transfer; regional ionosphere map (RIM); Allan deviation

郭敬雨, 左鸿铭, 龚晓鹏, 等. 不同电离层改正的PPP时间传递性能评估[J]. 导航定位学报, 2023, 11(3): 53-62.（GUO Jingyu, ZUO Hongming, GONG Xiaopeng, et al. Performance evaluation of PPP time transfer by different ionospheric correction strategies[J]. Journal of Navigation and Positioning, 2023, 11(3): 53-62.）

10.16547/j.cnki.10-1096.20230308.

P228

A

2095-4999(2023)03-0053-10

2022-08-24

国家自然科学基金项目（42174029，41904016）。

郭敬雨（1991—），男，河南周口人，硕士研究生，研究方向为PPP高精度时间传递。