多元回归格网改正量模型的大区域坐标转换方法

杨国创，尹 彤，王金月，高 严，孙泽宇

多元回归格网改正量模型的大区域坐标转换方法

杨国创1，尹 彤2，王金月3，高 严2，孙泽宇2

（1. 广东省地质测绘院，广州 510800；2. 自然资源部 测绘标准化研究所，西安 710054；3. 自然资源部 地图技术审查中心，北京 100036）

为了解决我国存量地理信息成果向2000中国大地坐标系（CGCS2000）的整体无缝转换问题，提出一种多元回归格网改正量模型的大区域坐标转换方法：采用格网改正量法建立统一的转换模型，格网节点改正量采用多元回归算法实现，待转点改正量采用双线性内插法获取，研究整套转换模型及其使用方法。实验结果表明，多元回归模型计算精度较高，且可保证转换结果的唯一性；格网改正量法是大区域转换的统一模型，能够实现大区域的无缝转换；格网转换方法效率高、可实施性强、准确度高。

2000中国大地坐标系（CGCS2000）；多元回归；格网改正量；双线性内插；坐标转换

0 引言

中国当前最新的国家大地坐标系2000国家大地坐标系（China geodetic coordinate system 2000，CGCS2000）是采用空间技术手段建立的高精度地心动态大地坐标系[1]。2008年7月启用之后，很多大地测量和测绘工程工作均基于CGCS2000框架展开。

由于之前我国先后采用1954北京坐标系和1980西安坐标系，所以在我国基础测绘及工程应用领域存在大量往期坐标系统成果资料，这些资料在我国的建设领域大量存在并产生着关键作用。CGCS2000的启用必然存在一个关键问题，即往期地理信息成果如何转换至CGCS2000坐标系下，如何采用一种通用方法完成全国海量的地理信息数据转换工作，可以考虑将格网改正量法应用到大区域成果坐标系统转换中。

目前，我国通过与空间大地网联合平差已获取了将近5万多个不同级别天文大地网点的CGCS2000坐标[2]，这些点在我国中东部地区分布较为均匀，西部地区依据地理环境和经济情况也整体覆盖；所以基于这些公共点可以实现1954北京坐标系、1980西安坐标系与CGCS2000之间的相互转换。

在文献[3-4]中，将反距离加权法和德劳奈（Delaunay）三角网法应用到我国速度场应用中，采用邻近点综合特征表述任一点特征并构建三角网的方法，效果很好。本文将重点研究如何利用公共点，采用多元回归模型，实现基于方形格网改正量的坐标转换方法，并结合某市的情况进行实验验证和精度分析。

1 基于多元回归模型的格网改正量计算方法

1.1 多元回归方程

多元回归方程是含有多个回归变量的多项式回归模型，在大地测量领域可用来转换不同参考框架之间的大地坐标或直角坐标[5]。在格网模型的格网节点改正量计算中可采用多元回归模型，通过搜索一定范围内的公共点及其坐标改正值来计算节点处的坐标改正值。其输入数据可以是搜索半径内符合条件的点，也可以是全部数据。因输入数据的数量影响模型计算速度，故可视情况而定。在每个格网节点处均须单独构建多项式曲面模型，根据每个节点半径范围内的所有公共点计算回归方程参数。

如图1所示，输入数据为节点周边半径范围内搜索的公共点，为搜索到的公共点个数，特征值为每个公共点的原坐标系和目标坐标系的经纬度差异（∆B,∆L）。

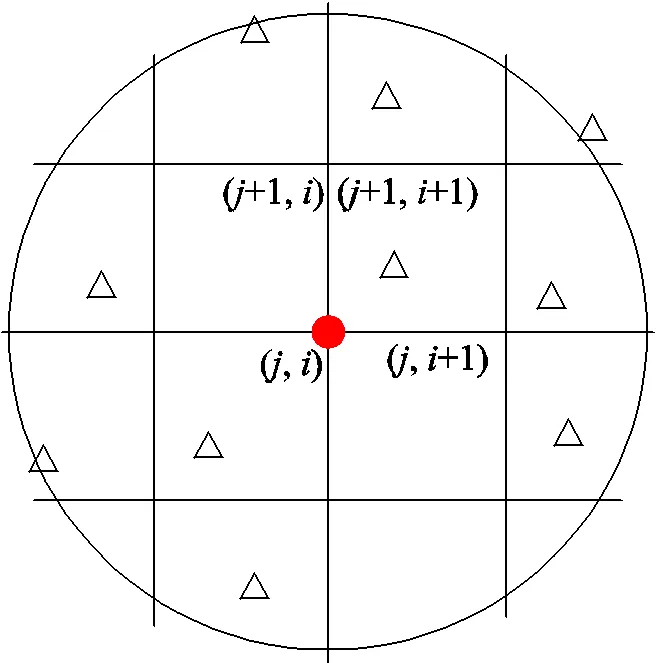
图1 格网节点处半径搜索（圆点为格网节点，三角为搜索到的公共点）

首先确定多元方程模拟量，计算节点半径范围内的每个公共点处2套坐标系统在纬度和经度位置的差异（∆B,∆L）（0<≤）；然后计算搜索范围内所有公共点的中心点位置（0,0）；最后根据以上数据在每个节点处构建多元回归多项式。节点处纬度和经度坐标改正量表达式为：

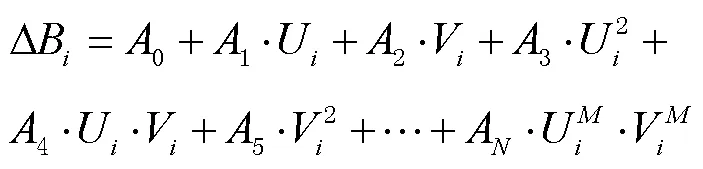
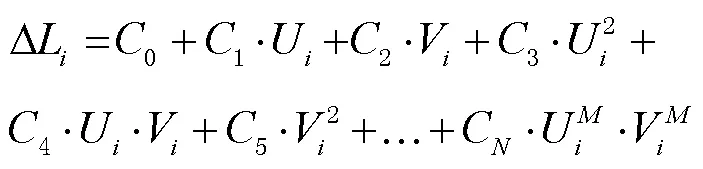
式中：A（0≤≤）为纬度特征项多项式系数；C为经度特征项多项式系数；U=B-0；V=L-0（B、L为节点在原坐标系的纬度和经度值）；为回归方程阶数。

将每个公共点处的经纬度差（∆B,∆L）以及U和V带入多项式中，形成组多项式方程，并采用最小二乘拟合计算A和C。最终将节点的经纬度带入多项式中，即可获取节点处的改正量值。0和0即为格网节点的坐标改正量估值[6]。

1.2 格网节点改正量数据存储

格网改正数据存储可以采用国际标准的格网文件格式，如：美国或加拿大大地测量局建立的标准格网格式[7-8]；一般研究中可以根据编程需要来设定。本文采用txt文本存储，存储格式为行号、列号、纬度改正量∆B、经度改正量∆L，同时配合元数据文件来说明格网起始经纬度和经纬度方向的格网间隔。

2 双线性内插算法

双线性插值是先后在2个方向或者2个变量上进行线性插值的算法。双线性内插法在矢量和影像转换中使用普遍，具有计算简单、转换结果平滑、过渡自然等特点[9-10]。本文涉及到如何通过格网4个节点经纬度坐标及对应的特征值，采用差值方法来获取格网内任意位置的特征值，即在经度和纬度方向上依次实施线性插值。如图2所示。

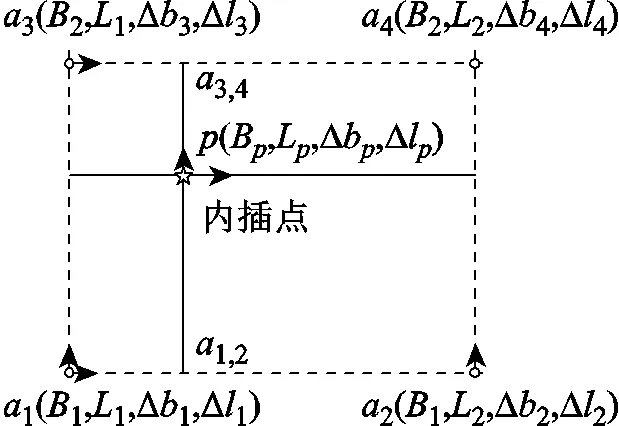
图2 格网内任意位置的双线性内插（圆圈为格网点，五星为内插点）

图2中，已知格网4个节点经纬度坐标和节点经纬度坐标转换改正量分别为1（1,1,∆1,∆1）、2（1,2,∆2,∆2）、3（2,1,∆3,∆3）、4（2,2,∆4,∆4）。内插点为待定点（B,L,∆b,∆l），其中位置参数（B,L）已知，需要计算特征参数坐标转换改正量（∆b,∆l）。

双线性内插算法首先在方向（东方向）上内插，然后在方向（北方向）内插。即先在纬度方向内插点1,2和3,4，然后由1,2和3,4内插点。具体流程如下（其中所有点的位置坐标已知）：

1）在1方向上进行线性内插，得到1,2（1,L,∆1,2,∆1,2），即：

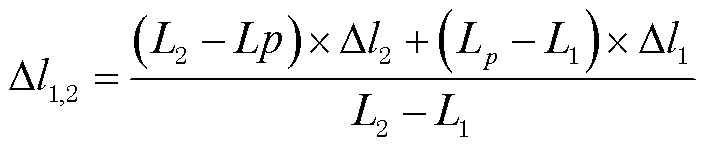
2）在2方向上进行线性内插，得到3,4（2,L, ∆3,4, ∆3,4），即：

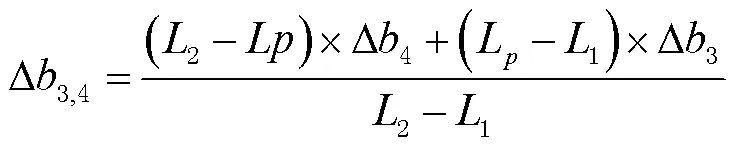
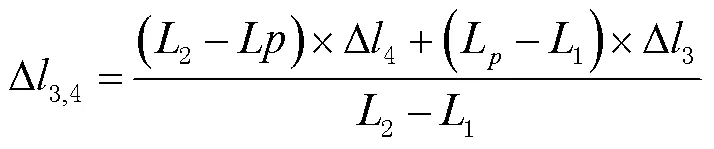
3）在B方向上进行线性内插，得到（B,p,∆b,∆l），即：

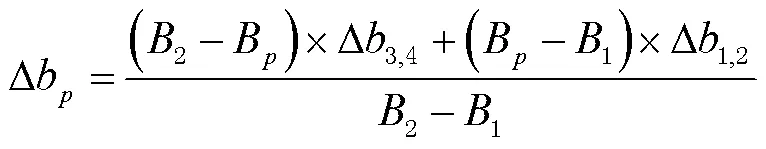
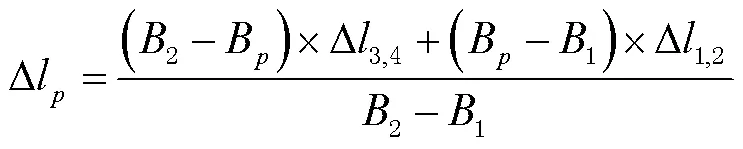
在这个模型中，只要输入区域内的任一点（格网内部、格网线上）的经纬度就可以插值该点的坐标改正量。坐标转换过程只需要在原坐标上加入改正量既可获取在目标坐标系的新坐标，从而可实现基于格网的坐标转换工作。转换后新的坐标为：

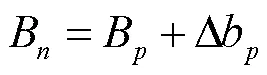
同时，在区域上插值获取的改正量具有连续性和唯一性特点[11]，这一点十分重要。

3 基于格网的坐标转换流程

改正量格网的坐标转换主要包括5个步骤：1）按照合适的经纬度间隔制作格网；2）基于公共点采用半径搜索法和多元回归方程计算格网节点处的坐标改正量；3）格网改正量文件制作；4）格网改正量文件精度验证；5）格网制作完毕后，基于格网文件采用双线性内插方法实现逐点坐标转换。

这个转换模型即顾及了公共点的空间相关性，又保证了区域转换的连续性，避免了图形间的接边误差，从而实现高精度、无缝隙的大区域坐标转换，其优势是小区域四参数、七参数等转换模型无法相提并论的。

3.1 区域改正量格网制作

格网制作的主要目的是确定格网上各个节点的经纬度值，首先确定格网起始经度和纬度值(0,0)，然后确定格网经纬度间隔（G,G），以及确定各个节点行列号（h,l）。

1）起始经纬度(0,0)的确定依据。依照转换区域的范围，一般采用长方形覆盖，须在所转换区域的边界向外延伸5 km。

2）格网间隔确定依据。所述格网点间隔是指建立格网的纵横相邻格网的经纬度等差异量，主要依据控制点的平均间隔。一般格网间隔要小于控制点的平均间隔，可以采用1″、1.5″或3″。

区域坐标改正量格网网形如图3所示。

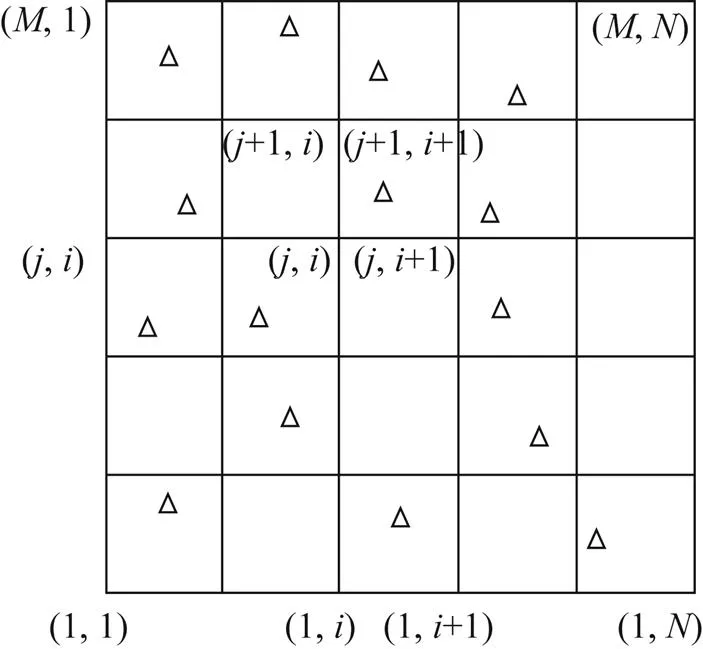
图3 区域格网网络覆盖（三角代表公共点）

3.2 基于多元回归计算格网节点改正值

采用多元回归方程，利用格网点周边公共点来计算格网节点处坐标改正量，如图4所示。

首先采用半径加四象限搜索法找到节点周边的公共点；然后将搜索到的公共点经纬度和原坐标系和目标坐标系的经纬度差异作为输入值，采用多元回归模型计算节点处的改正量。

遍历所有的格网节点之后，将节点及其改正量保存在文件中，以备坐标转换使用。可以绘制格网转换改正量分量图，来评估改正量模型的连续性和平缓性——从数值图来观察其连续性，一般情况下是连续的、平滑的、平缓的[12]。

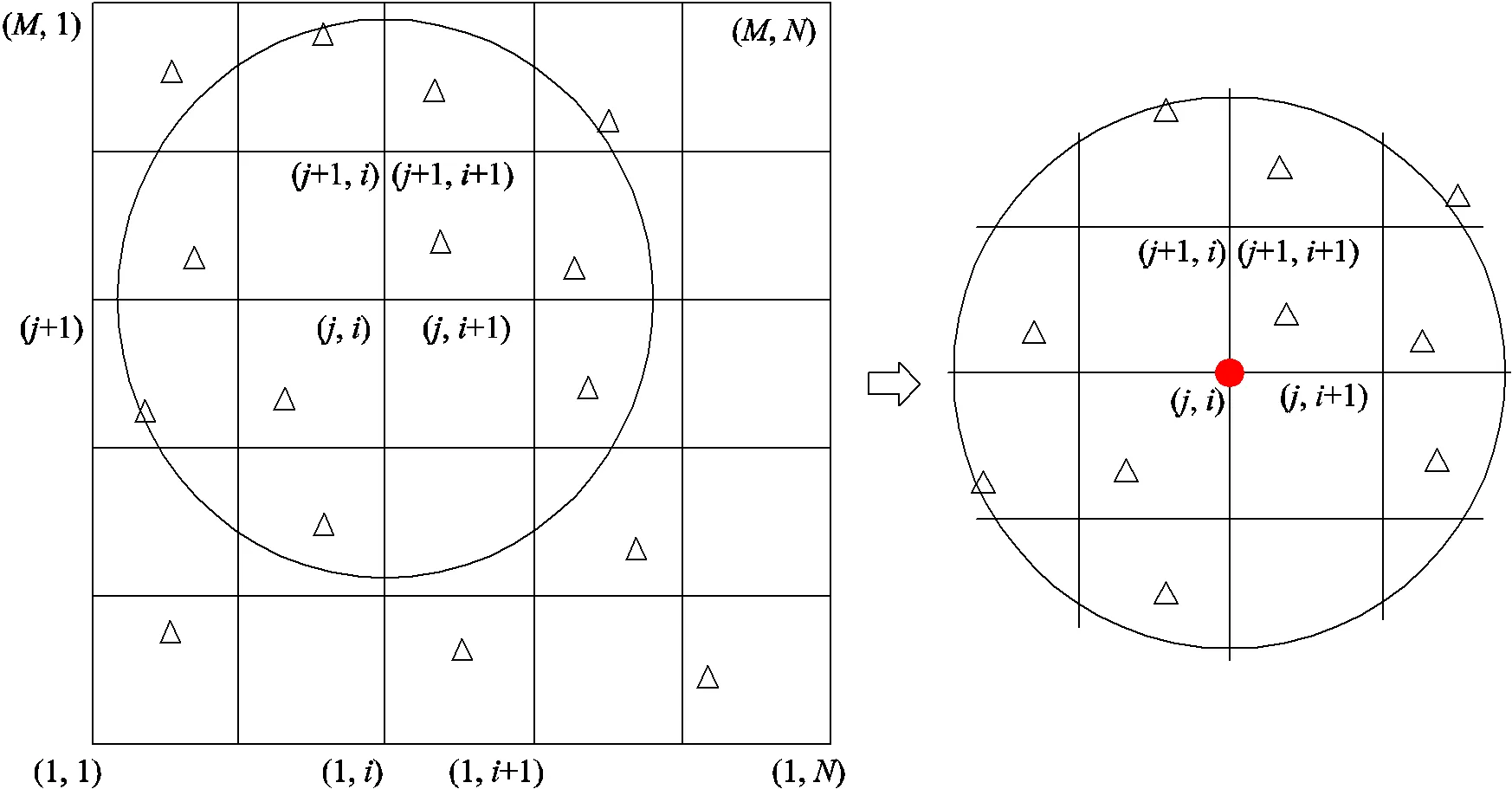
图4 基于多元回归的格网节点改正数计算（圆点为格网点，三角为公共点）

3.3 格网转换精度验证

为了保证格网改正量模型的正确性，须对格网文件进行连续性与符合性评估[13]。可以采用内符合精度和外符合精度验证。

1）内符合精度验证。为了保证格网改正文件的精度，需要采用内插方法对参与格网计算的公共点进行转换，并统计其转换后的精度。

2）外符合精度验证。采用外业实测的方法采集原坐标和目标系下的全球卫星导航系统（global navigation satellite system，GNSS）接收机测得的坐标，然后采用格网改正模型将原坐标下的GNSS成果转换至目标系下并与实测目标系成果进行比较。

4 实验与结果分析

4.1 实验数据概述

本次实验数据采用某市C级和D级点作为已知公共点，这些点均具有1980西安坐标系和CGCS2000坐标系成果，共计107个点（包括46个C级点、61个D级点）。公共点的经纬度坐标范围为34°20'N—36°07' N、108°23'E—109°55'E。

C级点和D级点的点位精度统计如表1所示。

表1 C级和D级点精度统计 mm

由于公共点分布比较均匀，确定本市改正量格网范围起始位置为108°20' E—109°58' E、34°17' N—36°10' N，格网经纬方向间隔均为1″，格网采用搜索半径为3″。公共点分布如图5所示。

图5 公共点分布（蓝色点将参与格网计算、红色点作为验证点）

4.2 格网改正量模型计算

根据前面确定的格网参数，计算并存储起始点位置及各个节点的行列号，保存在txt文件中。然后采用编写的多元回归格网算法软件逐个节点计算。其中选用97个点参与格网制作，其他10个点（C级点3个、D级点7个）作为外符合精度验证点。

输入文件为格网行列号文件、公共点文件、计算参数（搜索半径、起始点坐标等参数设置文件），经过约1.5 h的计算，获得格网改正量文件coordinate.dll。

4.3 采用双线性内插方法计算待转换点的改正量

读取转换图形或者文本的各个要素，并逐个根据待转换点的原始坐标确定其所在格网及4个节点的特征参数；采用双线性内插法以及格网中对应4个格网点的格网改正量确定待转换点的改正量；然后将待转点原坐标与改正量相加即可得到目标坐标系下的新坐标，并逐点逐要素实现转换。

4.4 精度分析

分别采用内符合和外符合检验的方法进行精度分析。

采用格网改正文件将公共点从原始坐标系转换至目标坐标系，然后与其目标坐标系的已知坐标进行比较。

内符合验证采用97个公共点，将其转换误差统计结果为：方向最小误差为1.1 mm，方向最大误差为9.2 mm，方向中误差为4.5 mm；方向最小误差为2.9 mm，方向最大误差为11.3 mm，方向中误差为6.2 mm。

同时，对转换精度误差区间分布进行统计：方向转换误差在0～5 mm区间的有65个点，方向转换误差在5～10 mm区间的有32个点，方向转换误差大于10 mm的有0个点；方向转换误差在0～5 mm区间的有33个点，方向转换误差在5～10 mm区间的有62个点，方向转换误差大于10 mm的有2个点。

外符合精度验证基于没参与格网改正模型计算的3个C级点和7个D级点，采用格网改正文件将公共点从原始坐标系转换至目标坐标系，然后跟其目标坐标系的已知坐标进行比较。外符合验证点转换误差统计为：

3个C级点外符合转换误差统计结果：方向最小误差为1.9 mm，方向最大误差为7.4 mm，方向中误差为4.8 mm；方向最小误差为4.1 mm，方向最大误差为5.8 mm，方向中误差为5.3 mm。

7个D级点外符合转换误差统计结果：方向最小误差为2.4 mm，方向最大误差为9.4 mm，方向中误差为6.9 mm；方向最小误差为5.3 mm，方向最大误差为11.3 mm，方向中误差为7.3 mm。

综合统计10个外符合点的坐标转换误差：方向坐标转换中误差为4.3mm，方向转换最小差异为2.0 mm，最大差异为9 mm；方向坐标转换中误差为7.1 mm，方向转换最小差异为4 mm，最大差异为11 mm。符合转换精度要求。

5 结束语

本文采用多元回归格网改正量模型进行地理信息数据的逐点无缝转换，经过理论分析和实验验证，得到以下几点结论：

1）国家坐标系统转换涉及到全国或各省海量数据的整体统一转换，格网改正量模型避免了传统的四参数或七参数转换的不足，能够实现转换前后图形元素的无缝接边；在格网模型所涉及的格网特征量计算方法、差值方法、格网间隔等参数固定的情况下，任意点的坐标转换结果是唯一的，确保了图件中点、线、面等元素的坐标转换结果的唯一性和统一性。

2）格网转换的本质是通过待转换点周边的控制点来实现坐标转换，距离转换点越近的公共点的特征表达权重越大，这种基于控制点的直接转换方法转换准确度和现势性更高；采用多元回归方程计算格网节点改正量的方法精度及其运算速度比较适合生产需求，且内外符合精度较好。

3）格网改正量模型可以根据区域进行任意切割使用，为转换参数的分区管理、加密处理和生产使用提供了方便，可操作性强，是我国开展大区域 CGCS2000坐标系统转换的实用方法。

[1] 郭充, 吕志平. 基于Bursa模型的格网坐标转换[C]// 测绘通报. 测绘科学前沿技术论坛摘要集. 北京: 测绘出版社, 2008: 979-983.

[2] 郭充. 面向CGCS2000的格网坐标转换方法及应用研究[D]. 郑州: 信息工程大学, 2009.

[3] 任营营, 王虎, 王解先, 等. 基于K-Means++的省内子块体划分及中国大陆水平相对运动速度场模型的建立与分析[J]. 地球物理学报, 2020, 63(7): 2516-2533.

[4] 任营营, 王解先, 王虎, 等. 基于局部无缝Delaunay三角网反距离加权法构建中国大陆速度场[J]. 武汉大学学报(信息科学版), 2021, 46(7): 1071-1080.

[5] 许琳琳. 分布式环境下的格网坐标转换方法与应用[D]. 郑州: 信息工程大学, 2012.

[6] 王惠文. 多元回归模型评价、模型分类以及模型预测理论研究及其应用[D]. 北京: 北京航空航天大学, 2013.

[7] 王凯时, 冯杨民, 刘立. 格网法在2000国家大地坐标系基准转换中的关键技术[J]. 测绘地理信息, 2022, 47(2): 15-18.

[8] 蒋光伟, 焦立芬, 田晓静, 等. 基于三角剖分与方向线拼接的高精度坐标转换格网模型的建立[J]. 大地测量与地球动力学, 2015, 35(2): 222-224.

[9] 朱毅, 丁云鹏, 李正会, 等. 利用三角剖分内插法精化似大地水准面模型[J]. 测绘科学技术学报, 2014, 31(6): 584-586.

[10] 赵辉, 张颜秋, 樊琦, 等. 基于格网模型的地理信息数据坐标转换[J]. 测绘与空间地理信息, 2020, 43(10): 201-203.

[11] 王谦, 赵俊三, 王涛, 等. 改进的高精度CGCS2000格网改正量自动计算模型设计与实现[J]. 地质灾害与环境保护, 2019, 30(3): 92-95.

[12] 郭充, 吕志平. 基于Bursa模型的格网坐标转换[C]// 测绘通报. 测绘科学前沿技术论坛摘要集. 北京: 测绘出版社, 2008: 979-983.

[13] 吕志平, 魏子卿, 李军, 等. CGCS2000高精度坐标转换格网模型的建立[J]. 测绘学报, 2013, 42(6): 791-797.

Large area coordinate transformation method based on multivariate regression grid correction model

YANG Guochang1, YIN Tong2, WANG Jinyue3, GAO Yan2, SUN Zeyu2

（1. Geology Surveying and Mapping Institute of Guangdong, Guangzhou 510800, China;2. Institute of Surveying and Mapping Standardization, Ministry of Natural Resources, Xi’an 710054, China;3. Supervision Center of Map, Ministry of Natural Resources, Beijing 100036, China）

In order to solve the overall seamless transformation of China's previous geographic information data results to the China geodetic coordinate system 2000 (CGCS2000), the paper proposed a large area coordinate transformation method based on multivariate regression grid correction model: the unified transformation model was established by using the grid correction model, by which the grid node correction was realized by multiple regression algorithm, and the correction of the points to be transformed was obtained by bilinear interpolation, to perform the calculation and application of the whole set of the transformation model. Experimental result showed that the multiple regression model could have high accuracy and ensure the uniqueness of the conversion result; and the grid correction method would be a unified conversion model of large area to help realize seamless conversion of large areas; moreover, the grid conversion method would have high efficiency, strong implementability and high accuracy.

China geodetic coordinate system 2000 (CGCS2000); multiple regression; grid correction; bilinear interpolation; coordinate transformation

杨国创, 尹彤, 王金月, 等. 多元回归格网改正量模型的大区域坐标转换方法[J]. 导航定位学报, 2023, 11(3): 185-190.（YANG Guochang, YIN Tong, WANG Jinyue, et al. Large area coordinate transformation method based on multivariate regression grid correction model[J]. Journal of Navigation and Positioning, 2023, 11(3): 185-190.）

10.16547/j.cnki.10-1096.20230325.

P228

A

2095-4999(2023)03-0185-06

2022-05-13

杨国创（1972—），男，广东阳春人，大学学历，测绘高级工程师，研究方向为大地测量、摄影测量技术应用及测绘管理。

尹彤（1989—），男，宁夏固原人，硕士，工程师，研究方向为定位与导航技术应用及测绘地理信息标准化。