基于Stanley序列的QC-LDPC码新颖构造方法

袁建国,蒯家松,张帅康

(重庆邮电大学 光电信息感测与传输技术重庆市重点实验室,重庆 400065)

0 引 言

低密度奇偶校验(low-density parity-check,LDPC)码作为一种逼近香农容量限、具有线性编译码复杂度的分组码[1-2],在通信系统中发挥着十分重要的作用。

准循环(quasi-cyclic,QC)LDPC码是一类重要的结构化LDPC码[3],其奇偶校验矩阵(parity-check matrix,PCM)具有准循环结构。构造良好的中长码长的QC-LDPC码,通常具有低错误平层[4]、译码可快速收敛、纠错性能优于随机LDPC码等优点。QC-LDPC码凭借编译码复杂度低、编译码可并行实现的优势,在移动通信、存储系统、深空通信、光通信等领域引起了广泛的关注[5]。

代数、组合等数学工具已被国内外学者用来设计性能优异的QC-LDPC码,如有限域[6]、循环差集[7]等。国内外研究表明,通过代数或组合工具能够构造出围长至少为6的QC-LDPC码[8-9]。在使用迭代算法进行译码时,短环(尤其4环)的存在会严重影响码字的纠错性能[10]。所以,设计具有大围长的QC-LDPC码更具有现实意义。

文献[11]提出一种利用Stanley序列中的元素去扩展原模图基矩阵来构造QC-LDPC码的构造方法,但是,其原模图基矩阵是通过渐进边增长(progressive edge growth,PEG)算法搜索而来,计算复杂度比较高,且构造出来的码字码长与Stanley序列中的元素相关,构造更短码长的QC-LDPC码会比较困难。因此,本文针对QC-LDPC码的短环结构会严重影响码字纠错性能的问题,基于文献[11]中提出的Stanley序列设计了一类围长至少为8的QC-LDPC码,且码长只与扩展系数相关,能够获得更短码长的码字,其构造方法简单且计算复杂度较低、易于硬件实现、纠错性能较好且无明显错误平层现象。

1 QC-LDPC码的构造方法

1.1 校验矩阵的构造

如果一类列重为J,行重为L的规则QC-LDPC码的零空间由奇偶校验矩阵H来表示,而奇偶校验矩阵H可以用循环移位矩阵(circulant permutation matrices,CPMs)和零矩阵(zero matrices,ZMs)来表示。且CPMs中的循环移位值构成了指数矩阵(exponent matrix,EM),用P=(ei,j)表示为

(1)

(1)式中：ei,j∈{-1,0,1,2,…,z-1}(z>0);J和L均为正整数,0≤i≤J,0≤j≤L。

当循环移位值ei,j=-1时,用大小为z×z的ZMs替换EM中相应位置的ei,j。当循环移位值ei,j≠-1时,用大小为z×z的CPMs替换EM中相应位置的ei,j,即可得到QC-LDPC码的奇偶校验矩阵H。因此,当CPMs的大小确定时,用CPMs对EM进行扩展得到奇偶校验矩阵H,CPMs大小用z×z来表示,z为扩展系数,奇偶校验矩阵表示为

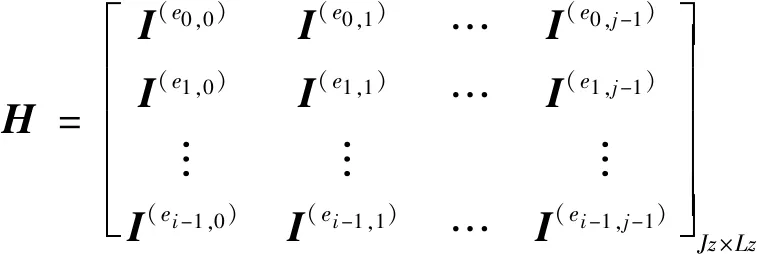
(2)

(2)式中,I(ei,j)表示由单位矩阵循环移位ei,j次得到的CPMs,其大小为z×z。

通过分析上述构造过程可以看出,构造QC-LDPC码等同于设计其奇偶校验矩阵H,而奇偶校验矩阵H是由其对应的EM扩展而来,因此,设计对应的EM是至关重要的一步。

1.2 环长分析

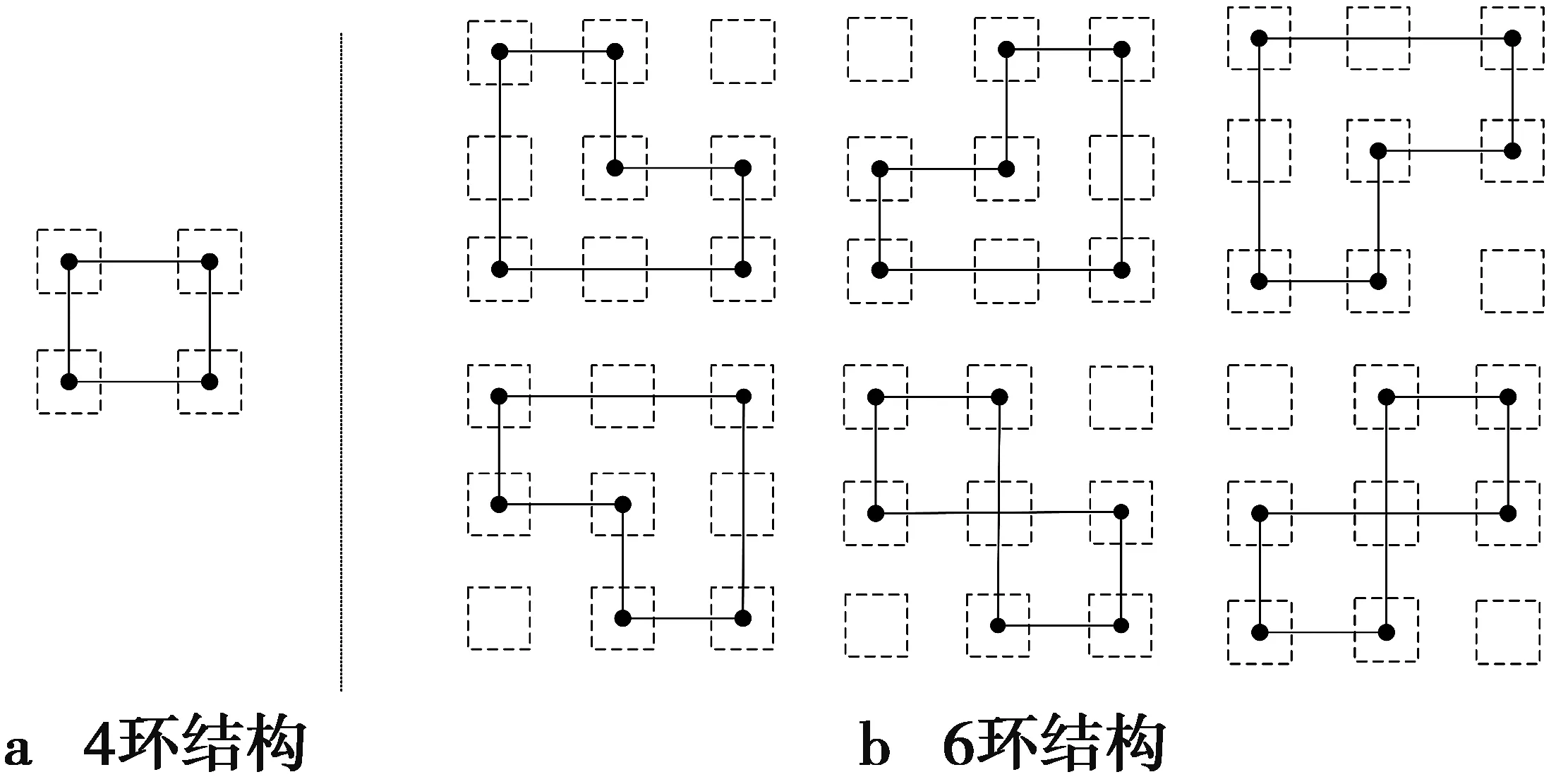
LDPC码的译码性能通常受环长、码字分布等影响,而短环的存在通常会导致译码不能完全收敛,严重影响码字纠错性能[12-13]。因此,在构造具有良好纠错性能的LDPC码时,至少要避免其奇偶校验矩阵Tanner图中不存在4环。研究表明,Tanner图中的环通常受指数矩阵和移位系数大小的影响,如引理1所述。

引理1[1]若QC-LDPC码的指数矩阵为(3)式所示,则该码字存在2n环的充分必要条件为(3)式成立。

(3)

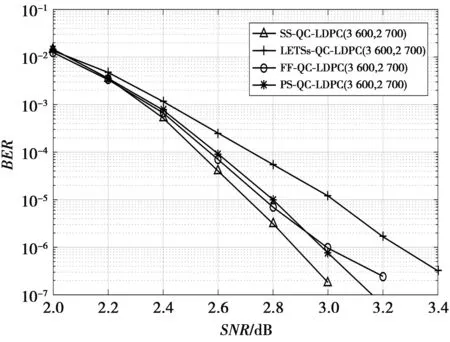
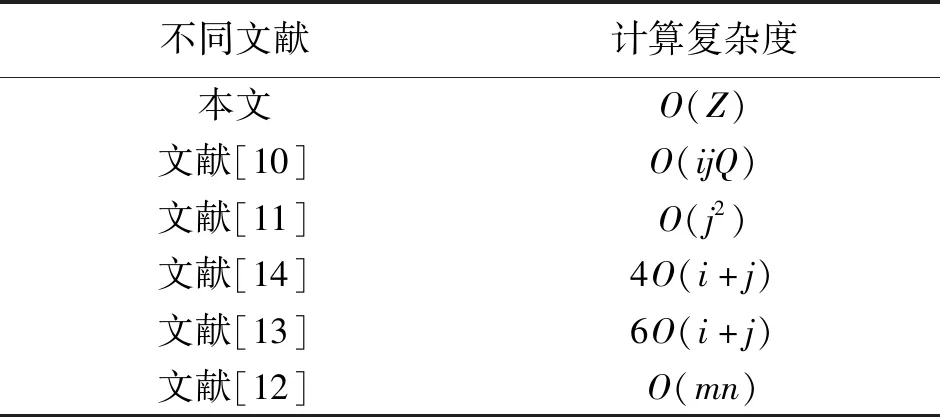
(3)式中：0≤jk

引理1指出了QC-LDPC码中环存在的条件,因此,在构造循环移位矩阵时,为避免短环,只需考虑搜索指数矩阵P中不满足(3)式的非负数值即可。

1.3 有限域构造

基于有限域的QC-LDPC码构造是一种经典代数方法[14]。若素域GF(Q)={0,1,…,Q-1},从GF(Q)中任意选择若干个数组成集合w1={i0,i1,i2,…,iM-1}(M

ei,j=ir×js(modQ)

(4)

(4)式中：0≤r

因此,当集合w1和w2中的值确定后,通过(4)式计算出循环移位值即可得到相应的指数矩阵。

2 Stanley序列

文献[11]已证明Stanley序列与最大公约数(greatest common divisor,GCD)条件之间是一种等价关系,因而在介绍Stanley序列之前,这里先简要介绍GCD条件,如引理2所述。

引理2[15]设x、y和t为3个行索引值,且0≤x

(dt-dx)/gcd(dt-dx,dy-dx)≥L

(5)

(5)式中,gcd(dt-dx,dy-dx)表示dt-dx和dy-dx的最大公约数。

文献[11]给出了计算Stanley序列中元素的方法,如引理3所述。

引理3[11]假设Stanley序列为S(h)={h0,h1,…,h∂-1},∂为正整数,符号v2(∂)表示最大非负正整数f满足2f|∂(∂能被2f整除)条件,则序列S(h)中第∂个元素可以通过(6)式计算得到。

(6)

(6)式中,u为正整数。

3 基于Stanley序列的QC-LDPC码构造方法

3.1 构造方法

本文考虑构造一类(J,L)QC-LDPC码,其具体的构造步骤如下。

步骤1构造集合ai。基于Stanley序列的特殊性质,考虑从该序列中任意选择L个元素构成集合ai={a0,a1,…,aL-1},且a0

步骤2构造集合bj。由引理1给出的环长存在充要条件,(3)式可等价于(7)式。

(7)

(7)式中：aik∈ai;bjk∈bj;bj0=bjn;aik≠aik+1;bik≠bik+1。

要使构造的QC-LDPC码奇偶校验矩阵Tanner图中不存在4环和6环,只需保证当n分别为2和3时,集合ai和bj中所有元素均满足(7)式不成立即可。因此,可通过验证集合ai和bj中的值是否满足(7)式在n=2和n=3时不成立来设计穷举算法。其搜索过程如下。

①确定z的值,z为任意正整数;

②若直接进行搜索,计算复杂度较高,这里先进行预处理。进一步分析环长存在的充要条件可知,当L=3时,其计算复杂度进一步降低,此时集合ai={a0,a1,a2},a0

③当n分别为2和3时,把步骤②得到的集合ai={a0,a1,a2}代入到(7)式中,在[0,z]依次搜索出使(7)式不成立的元素构成集合bj。为了进一步降低搜索难度,考虑先在[0,z]确定一个子集,如{0,1,2,…,9},先搜索该子集中使(7)式不成立的元素并选出3个元素{b1,b2,b3}(b1

④从步骤③得到的集合bj中任意选择J个元素构成集合bj={b0,b1,b2,…,bJ-1},且b0

步骤3构造指数矩阵P。利用步骤①和②得到的2个集合ai和bj,通过(4)式依次计算出对应的循环移位值ei,j,即可得到对应的指数矩阵P。

步骤4构造奇偶校验矩阵H。考虑用大小为Q×Q(Q≥z)的CPMs替换步骤④构造的指数矩阵P中对应位置的循环移位值,即得到其奇偶校验矩阵H。

通过步骤1—步骤4,进一步构造出一类码长为QL,码率为(L-3)/L的规则QC-LDPC码。

3.2 无4、6环证明

QC-LDPC码奇偶校验矩阵Tanner图中4环和6环存在类型如图1所示。

图1 4环和6环的结构图Fig.1 Structure chart of girth-4 and girth-6

根据引理1给出的环长存在充要条件可知,若所构造的QC-LDPC码的奇偶校验矩阵Tanner图中不存在4、6环,有(8)式成立。

(8)

1)无4环证明。

图1a给出了4环存在的结构,若其奇偶校验矩阵对应的Tanner图中不存在4环,可将(8)式展开成n=2的特殊形式,表示为

(ej0,l0-ej1,l0)+(ej1,l1-ej2,l1)≠0(modQ)

(9)

因为循环移位值ei,j是通过(4)式计算得到,即ei,j=aibj(modQ),显然(10)式成立。

0<(ej0,l0-ej1,l0)+(ej1,l1-ej2,l1)

(10)

因此,当移位系数满足Q≥z时,所设计QC-LDPC码的奇偶校验矩阵Tanner图中不含4环。

2)无6环证明。图1b给出了6环存在的6种结构,若其奇偶校验矩阵Tanner图中不存在6环,可将(8)式展开成n=3的特殊形式,表示为

(ej0,l0-ej1,l0)+(ej1,l1-ej2,l1)+(ej2,l2-ej3,l2)≠

0(modQ)

(11)

根据Stanley序列的特殊性质,并进一步分析本文所述的构造方法可知,集合ai和bj中所有的元素均满足(7)式不成立,而对应的循环移位值由公式ei,j=aibj(modQ)计算得到,显然(12)式成立。

0<(ej0,l0-ej1,l0)+(ej1,l1-ej2,l1)+

(ej2,l2-ej3,l2)

(12)

因此,当移位系数满足Q≥z时,所设计的QC-LDPC码的奇偶校验矩阵Tanner图中不含6环。

4 仿真结果与性能分析

本文采用MATLAB软件进行仿真验证所构造的SS-QC-LDPC码的纠错性能,采用二进制相移键控(binary phase shift keying,BPSK)进行调制,采用加性高斯白噪声(additive white Gaussian noise,AWGN)信道,译码算法选择置信传播(belief propagation,BP)算法,考虑到译码复杂度与纠错性能的折中,在码率分别为0.5和0.67时,译码迭代次数分别选取为50次和40次。

考虑行重J=6,列重L=3,构造出一类码率为0.5的QC-LDPC码。取z值为200时,得到集合ai={1,3,4}、bj={2,6,24,26,31,67}。当移位系数Q=400时,得到一个码长2 400的规则QC-LDPC码,记为SS-QC-LDPC(2 400,1 200)码。当Q=200时,得到一个码长为1 200的QC-LDPC码,记为SS-QC-LDPC(1 200,600)码。构造出的指数矩阵结构表示为

(13)

当码长为2 400时,将所构造的SS-QC-LDPC (2 400,1 200)码与文献[10]基于Hoey序列(Hoey sequence,HS)构造的围长至少为8的规则HS-QC-LDPC(2 400,1 200)码、文献[11]基于原模图(protograph,P)和Stanley序列构造的围长为8的非规则PS-QC-LDPC(2 400,1 200)码、文献[14]基于同构(isomorphism,I)理论构造的规则I-QC-LDPC(2 400,1 200)码和文献[12]基于消除无叶基本陷阱集(leafless elementary trapping sets,LETSs)和原模图构造的非规则LETSs-QC-LDPC(2 400,1 200)码进行性能对比。

不同QC-LDPC码的BER与信噪比(signal-to-noise ratio,SNR)之间的性能仿真曲线如图2所示。由图2可知,当BER为10-6时,本文所构造的SS-QC-LDPC(2 400,1 200)码比HS-QC-LDPC(2 400,1 200)码、PS-QC-LDPC(2 400,1 200)码、I-QC-LDPC(2 400,1 200)码和LETSs-QC-LDPC(2 400,1 200)码的净编码增益(net coding gain,NCG)分别提升了约0.11、0.12、0.37和0.64 dB。

图2 SS-QC-LDPC(2 400,1 200)码与其他4种码字的性能仿真图Fig.2 Performance simulation chart of the SS-QC-LDPC(2 400,1 200) code with the other four code-words

码长为1 200时,将所构造的SS-QC-LDPC(1 200,600)码与文献[10]构造的规则HS-QC-LDPC (1 200,600)码、文献[14]构造的规则I-QC-LDPC(1 200,600)码和文献[12]构造的非规则LETSs-QC-LDPC(2 400,1 200)码进行性能仿真对比。

不同QC-LDPC码的BER与SNR之间的性能仿真曲线如图3所示。由图3可知,当BER为10-6时,本文构造的SS-QC-LDPC(1 200,600)码与I-QC-LDPC(1 200,600)码、HS-QC-LDPC(1 200,600)码和LETSs-QC-LDPC(1 200,600)码相比,其NCG分别提升了约0.75、0.74和0.95 dB。

图3 SS-QC-LDPC(1 200,600)码与其他3种码字的性能仿真图Fig.3 Performance simulation chart of theSS-QC-LDPC(1 200,600) code with the other three code-words

进一步分析图2可知,码长为2 400,BER为10-6时,所构造的SS-QC-LDPC(2 400,1 200)码和HS-QC-LDPC(2 400,1 200)码、PS-QC-LDPC(2 400,1 200)码相比,其NCG提升不明显,但HS-QC-LDPC(2 400,1 200)码在高SNR时出现了错误平层现象,而PS-QC-LDPC(2 400,1 200)码是通过扩展原模图基矩阵构造的,其原模图基矩阵是通过PEG算法搜索而来,计算复杂度较高。同样,当BER为10-6时,SS-QC-LDPC(2 400,1 200)码和I-QC-LDPC(2 400,1 200)码、LETSs-QC-LDPC(2 400,1 200)码相比,其NCG提升较大,其原因是I-QC-LDPC(2 400,1 200)码的校验矩阵Tanner图中有6环存在,影响了码字纠错性能。而LETSs-QC-LDPC(2 400,1 200)码虽然是基于消除无叶基本陷阱集构造的,但在构造过程中未完全避免校验矩阵Tanner图中6环的存在,因而其纠错性能较差。进一步分析图3可知,在高SNR区域,I-QC-LDPC(1 200,600)码和HS-QC-LDPC(1 200,600)码出现了明显错误平层现象,所构造的SS-QC-LDPC(1 200,600)码的NCG与LETSs-QC-LDPC(2 400,1 200)相比提升较大且无错误平层现象。

为进一步说明本文所构造的QC-LDPC码的性能,考虑行重J=9、列重L=3,构造出一类码率为0.67的QC-LDPC码。取z值为200,此时集合ai={1,3,4}、bj={1,2,6,7,24,26,31,67,72}。当移位系数Q=400时,得到一个码长为3 600的规则QC-LDPC码,记为SS-QC-LDPC(3 600,2 700)码。其指数矩阵的结构表示为

(14)

为不失一般性,将所构造的SS-QC-LDPC(3 600,2 700)码与文献[11]构造的PS-QC-LDPC(3 600,2 700)码、文献[14]基于有限域(finite field,FF)构造的规则FF-QC-LDPC(3 600,2 700)码和文献[12]构造的非规则LETSs-QC-LDPC(3 600,2 700)码进行性能仿真对比。

不同QC-LDPC码的BER与SNR之间的性能仿真曲线如图4所示。由图4可知,当BER为10-6时,本文构造的码长为3 600的SS-QC-LDPC(3 600,2 700)码与FF-QC-LDPC(3 600,2 700)码、PS-QC-LDPC (3 600,2 700)码和LETSs-QC-LDPC(3 600,2 700)码相比,其NCG分别提升了约0.13、0.11和0.4 dB。

图4 SS-QC-LDPC(3 600,2 700)码与其他3种码字的性能仿真图Fig.4 Performance simulation chart of the SS-QC-LDPC(3 600,2 700) code with the other three code-words

进一步分析图4可知,码率为0.67,BER为10-6时,本文构造的SS-QC-LDPC(3 600,2 700)码与FF-QC-LDPC(3 600,2 700)码和PS-QC-LDPC(3 600,2 700)码相比,其NCG均有一定的提升,而且FF-QC-LDPC(3 600,2 700)码在高信噪比区域有明显的错误平层。在高SNR区域,PS-QC-LDPC(3 600,2 700)码和LETSs-QC-LDPC(3 600,2 700)码虽然无明显错误平层,但是本文构造的SS-QC-LDPC(3 600,2 700)码的纠错性能优于PS-QC-LDPC(3 600,2 700)码和LETSs-QC-LDPC(3 600,2 700)码。

因此,由图2—图4可知,本文构造的码字在长码长、短码长以及高码率情况下均具有较好的纠错性能且无错误平层现象。

5 复杂度分析

本文涉及的复杂度分析主要是校验矩阵H构造过程的计算复杂度和编码过程的计算复杂度分析。在相同码长、码率的条件下,本文构造的QC-LDPC码与其他对比文献构造的码字均是基于生成矩阵编码的,因而编码的计算复杂度相同。不同的是在构造校验矩阵H过程中涉及的方法不同,因此,这里只需要针对在构造H时所涉及的计算复杂度进行分析即可。

进一步分析本文构造方法的构造步骤可知,在构造校验矩阵时,通过在给定范围内搜索满足无4、6环条件的元素,得到集合bj,其计算复杂度为O(z)。文献[10]中,其构造的指数矩阵由H1和H2两部分组成,矩阵H1是从Hoey序列中选出某些特定的元素构成的,H2是通过推导出的避免4、6环的2个条件计算而来,其计算复杂度为O(ijQ)。文献[11]是利用Stanley序列中的元素扩展原模图基矩阵构造,其原模图基矩阵是通过PEG算法搜索而来,因而其计算复杂度为O(j2)。文献[14]中,先利用有限域上的2个集合求出矩阵Po,使用加法规则求出矩阵Po的同构矩阵PI,再求出完全连通指数矩阵,最后得到非同构码,计算过程主要是对矩阵的排列和最优值的搜索,因而其计算复杂度为4O(i+j)。文献[13]中,先基于有限域获得基矩阵,再通过推导出的避免6环的6个条件去计算出最优值,其计算复杂度为6O(i+j)。文献[12]中,先使用外部信息传输分析获得原模图LDPC码的阈值,再使用分层搜索算法消除校验矩阵H的子矩阵对应子图中的LETSs,其计算复杂度为O(mn)。综上所述,本文与其他文献的计算复杂度对比分析情况如表1所示。(上述m、n分别表示校验矩阵的行数和列数,i、j分别表示指数矩阵的行数和列数)。

表1 本文与其他文献的计算复杂度对比Tab.1 Comparison of the computational complexity between this paper and other documents

通过上述分析可知,本文构造校验矩阵的计算复杂度与扩展系数z呈线性关系,与其他对比文献相比,具有较低计算复杂度。此外,本文的构造方法只需要存储2个集合以及扩展系数即可,其他元素只需要通过四则运算以及模除运算即可得到,其参数元素存储量也比较小。

6 结束语

本文利用Stanley序列的特殊性质,并结合穷举搜索算法提出一种QC-LDPC码的新颖构造方法,该构造方法所构造的奇偶校验矩阵Tanner图中不存在环4和环6,且码长只与扩展系数z相关,构造更短码长的码字比较容易。仿真结果表明,在相同条件下,本文所构造的SS-QC-LDPC(2 400,1 200)码、SS-QC-LDPC(1 200,600)码和SS-QC-LDPC(3 600,2 700)码与同码率、同码长的其他码字相比,其NCG在一定程度上均有提升,纠错性能较好且无明显错误平层现象。此外,该构造方法的计算复杂度与其他对比文献的构造方法相比较低。