一种并联机构全关节逆运动学分析方法

孙 涛，王 梁，霍欣明，齐 杨，王 俊，李 祺

一种并联机构全关节逆运动学分析方法

孙 涛1，王 梁1，霍欣明1，齐 杨2，王 俊3，李 祺3

(1. 天津大学机构理论与装备设计教育部重点实验室，天津 300350；2. 天津职业技术师范大学机械工程学院，天津 300222；3. 天津市航天机电装备研究所天津市航天智能装备技术重点实验室，天津 300301)

机器人机构逆运动学分析是开展其性能建模和优化设计的基础．然而，现有并联机构运动学逆解方法主要是针对给定位姿下驱动关节运动变量的求解，而对于非驱动关节运动变量则需基于机构的几何特性，通过反复迭代消元计算获得，因而难以形成代数化求解流程和数字化分析软件．针对上述问题，提出一种基于有限旋量的并联机构全关节位置逆解求解方法并开展其数字化软件研发．首先，提出并联机构全关节位置解求解流程，构造并联机构末端及其支链的初始位姿，利用有限旋量建立运动方程，并通过数值方法对运动方程进行求解．以一类两转动并联机构4RSR-SS为例，计算各支链的全关节位置解，并与仿真结果对比验证解的准确性．然后，在此基础上，建立全关节位置解的数字化算法，基于B/S架构开展并联机构运动学分析软件开发，构建运动学逆解、轨迹仿真和工作空间等功能模块，通过对3-PRS并联机构的全关节逆运动学分析验证软件的有效性．最后，从冗余参数、方程数目等方面与现有方法进行比较．提出的全关节逆运动学分析方法的优点在于：可构建简洁的运动方程并同时求解给定目标位姿下的所有关节变量，避免冗余参数和计算；涉及的所有步骤均可利用代数运算求解，有利于实现并联机器人机构逆运动学分析的数字化．

逆运动学；并联机构；有限旋量；数字化；运动学分析软件

并联机构由于具有运动灵活、刚度性能好、响应速度快等优点而显示出广阔的应用前景[1-2]．逆运动学旨在分析机器人机构关节空间与操作空间的运动映射，是开展静力学及动力学建模、设计的基础．并联机构同时含有驱动关节和被动关节，前者决定了机构的输出运动特性，后者则对轨迹规划、工作空间分析以及碰撞安全性检测具有重要意义．因此，并联机构的逆运动学不仅应求解给定末端动平台位姿下的驱动关节运动，也应构建被动关节运动变量与末端运动的关系．

现有的并联机构逆运动学分析方法可分为两类：基于位移方程[3]和基于运动方程[4]．位移方程法以闭环矢量法[5]为代表，利用三维矢量描述机构的位置和姿态，进而建立关节、支链和末端位姿之间的位移映射关系[6]．闭环矢量法能够快捷地求出驱动关节运动变量，但是仍涉及大量分析推导．运动方程法以D-H 法[7]为代表，主要利用含有关节运动变量的齐次变换矩阵描述关节运动，基于机构末端运动与支链末端运动相同的原理构造运动方程．该类方法更有助于实现非驱动关节的快速求解，但是齐次矩阵中含有的元素较多，需要对方程进行筛选．基于齐次矩阵的代数特征，衍生出了矩阵李群、对偶四元数等代数方法．Wang等[8]利用矩阵李群对一种三自由度2PUR-2RPU机构进行了逆运动学分析．Yang等[9]利用对偶四元数对一类空间闭环机构进行了逆运动学分析．Aspragathos等[10]从计算成本等方面比较了上述3类数学体系，并指出相比于齐次矩阵，矩阵李群和对偶四元数方法具有表达格式紧凑、计算便捷的优点．然而，需要注意的是，运动方程法描述机构和支链从初始状态至目标状态的运动．由于缺乏对一般并联机构的初始化描述研究，目前该方法尚局限于特定并联机构的逆运动学求解．

近年来，随着计算机技术的发展，运动分析数字化软件为实现不同并联机构高效运动学求解提供了新思路，已成为重要的发展趋势．Gosselin[11]基于Matlab率先提出了球面并联机构位置、工作空间、灵巧度与奇异性分析的可视化软件SMAPS．Kucuk 等[12]和Inner等[13]则分别针对平面并联机构和六自由度并联机构开展了正逆运动学、奇异性和工作空间分析，设计了SIDEP和STEWSIM两款软件．针对平面并联机构与空间三平动并联机构的正逆运动学，Gil等[14]开发了基于Java 3D技术的并联机构运动学示教软件．与串联机构相比，并联机构具有复杂多样的拓扑结构，传统方法难以针对不同并联机构实现逆运动学模型的系统化构建，因此制约了上述软件的适 用性．

针对上述并联机构逆运动学分析及其数字化软件研发中的难点问题，本文拟提出一种基于有限旋量的全关节逆运动学分析方法，并开展数字化研究．有限旋量是描述刚体连续运动的最简格式，以此作为数学工具可以统一、同步地求出机构的全关节运动变量．而且有限与瞬时螺旋理论可以将并联机构的整个建模、分析、设计过程统一于一个数学框架内，使得逆运动学与其他运动学、静力学、动力学建模分析不会割裂．

本文旨在建立通用有效的并联机构全关节逆运动学分析的方法流程，并探索数字化实现方法．全文讨论基于有限旋量理论的并联机构全关节解的方法流程，并开展算例验证，提出并联机构全关节位置逆解的数字化算法，构建在线运动学分析软件，从冗余参数、方程数目等方面讨论本方法与现有方法的区别.

1 并联机构全关节逆运动学建模方法

如图1所示，刚体从初始位姿运动至目标位姿所经历的连续运动可以视为螺旋运动[15]．基于有限旋量理论，该刚体运动在坐标系中可描述为

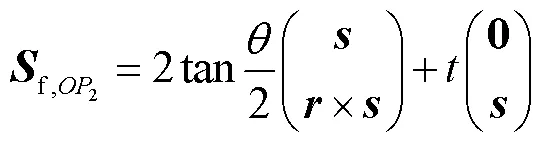
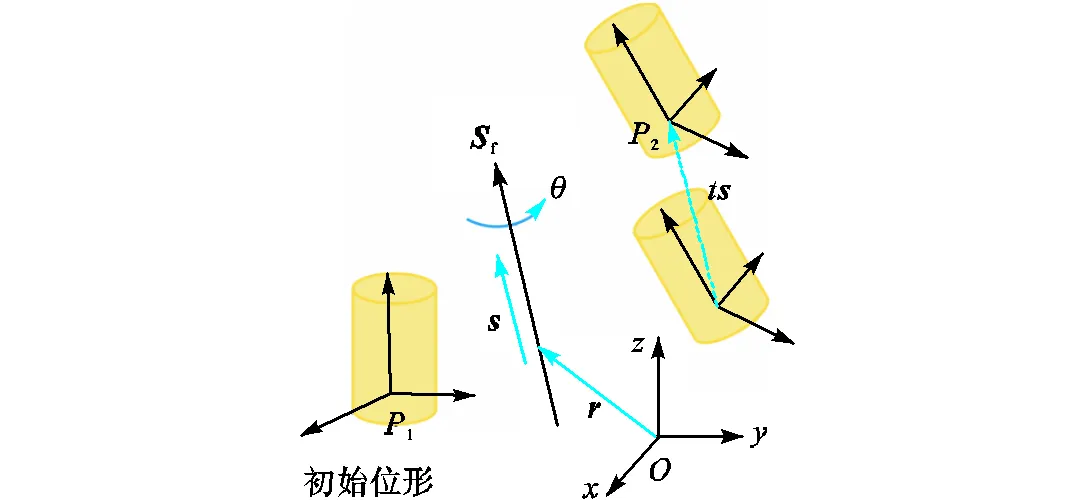
图1 刚体连续运动

并联机构单自由度关节的运动均可以看作是一个部件相对于另一部件的旋转或平移，因此可以用有限旋量描述．串联运动链的连续运动是关节运动的累积，由有限旋量三角积计算．并联机构由两个或两个以上的支链连接静平台和动平台，需要注意的是，每个支链的末端运动与并联机构动平台的运动相同，动平台的连续运动可以用各支链连续运动的交集表示．受此启发，本文提出了一种并联机构全关节逆运动学建模方法，如图2所示．

步骤1 机构初始化．

运动学描述动平台和运动关节从初始位姿到目标位姿的运动，因此，在构建运动方程时，须定义动平台的初始位姿并获得此位姿下关节运动轴线方位．为便于对机构进行初始化，本步骤提出了支链虚拟位姿的构建方法，将在第1.1节中详细阐述．

图2 并联机构逆运动学方法

步骤2 运动学建模．

并联机构的运动学建模可分为两个运动阶段：第1阶段是从虚拟位姿到初始位姿；第2阶段是从初始位姿到目标位姿．所有关节从初始位姿到目标位姿的运动变量可以通过两个阶段的关节运动相减来 求解．

步骤3 运动变量求解．

关节的旋转角度和平移位移被视为逆运动学方程的未知变量，关节运动的合成使得逆运动学方程呈现非线性的特点，难以计算求解，因此，将非线性的运动学方程求解转化为优化问题，并采用数值算法进行求解．在寻找精确解之前，先通过遗传算法获得变量的初始值以提高计算效率．

1.1 机构初始化

如图3所示，动平台和关节的目标位姿由它们相对初始位姿的角度或线位移来描述，在逆运动学问题中将它们视为运动变量．动平台的初始位姿可以在可达工作空间内任意选择，但是由于其他支链的约束，此时无法直接确定支链中关节的初始位姿，因此，需要通过定义虚拟位姿来初始化动平台及其对应的关节空间．

图3 初始位姿和目标位姿

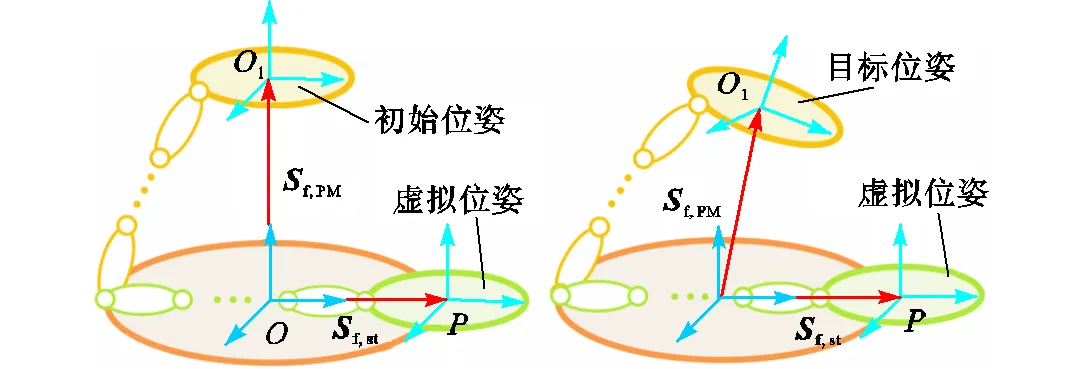
（a）虚拟位姿到初始位姿 （b）虚拟位姿到目标位姿

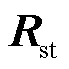
1.2 运动学建模

在完成机构初始化后，利用有限旋量构建机构的运动方程．并联机构末端动平台的连续运动可以表示为各支链连续运动的交集

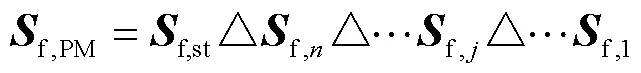
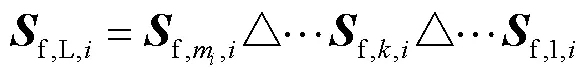
1.3 运动变量求解

对于具有-DoF运动关节的支链，存在个未知变量．为了降低计算成本，将方程分两个阶段求解，如图5所示．

在获得运动变量的基础上，第条支链第个关节的连续运动可表述为

方程右侧可简化为六维向量形式

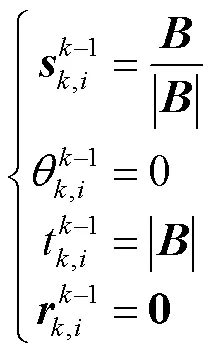
目标位姿下第条支链中第个关节的方向和位置向量可以描述为

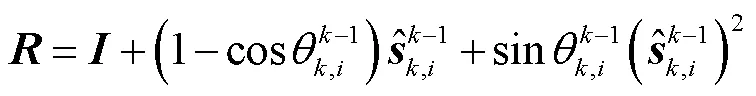
利用上述方法，可获得动平台任意目标位姿下所有关节的瞬时运动，此外，还可用于建立雅可比矩阵.

1.4 算 例

求解该并联机构机构的全关节运动学逆解．定义4条RSR支链和SS支链的虚拟位姿分别为动平台与静平台重合和SS杆垂直于静平台，此时

根据式(6)，RSR支链的连续运动可以描述为

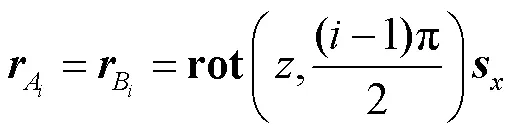
RSR支链中S关节的位置向量为

不考虑沿连杆方向的局部自由度，SS支链的运动可等效为SU支链，其末端运动为

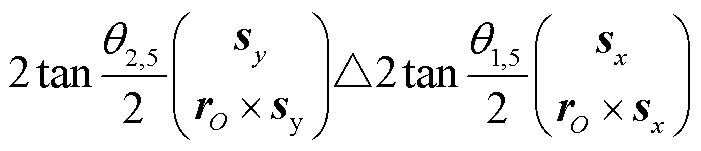
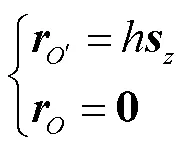
基于式(18)～(20)，构建Helix机器人的全关节运动方程

由于RSR和SS支链均少于6自由度，因此方程组(25)是超定的，解的迭代初始值应首先通过遗传算法获得，然后通过数值优化方法得到精确解，算法流程与图5一致．给定初始位姿和移动轨迹

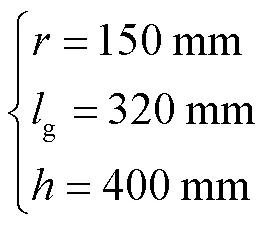
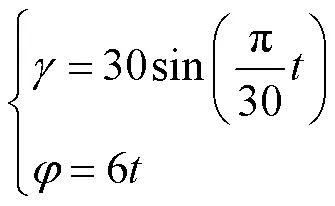
图7 第1支链和第2支链非驱动关节变量

图8 驱动关节的运动学变量

2 并联机构逆运动学数字化分析软件

快速准确地求解并联机构全关节运动学逆解对实现机器人轨迹规划、工作空间分析和运动检测具有重要意义．基于有限旋量的运动学求解方法无须利用经验进行判断，便于编程实现．本节拟开展并联机构逆运动学分析的数字化软件设计．

2.1 软件架构和设计

该软件旨在实现并联机构的运动学建模和分析，基于有限旋量的并联机构全关节逆运动学逆解数字化实现算法如下．

选择机构，输入尺度参数

选择功能模块

输入初始、目标位姿和相应约束条件

识别支链数量，对于支链执行

选择迭代步长和求解范围[min，max]

调用遗传算法解得初值

超定，调用数值优化算法求解精确解

恰定，调用迭代算法求解精确解

将解代回方程验证

if 验证通过

end

else

返回并重新确定初始值

输出结果

生成图形

end

end

软件共包含3个模块：逆运动学求解、轨迹仿真和工作空间分析，如图9所示．

图9 功能模块和输入输出

机构类型和尺度是3个功能模块共享的输入，其他不相同的输入参数作为3个模块各自独立的输入.

逆运动学模块主要是求解并联机构在给定目标位姿下的运动变量．当机构及其参数、初始位姿和目标位姿确定后，就可以得到从初始位姿到目标位姿的所有关节的运动变量．

轨迹模拟模块旨在检查在几何约束下机构的运动轨迹是否可行，几何约束由用户根据具体应用给出．在轨迹模拟中，如果关节运动违反给定的约束，机器人停止运动并响起警报，这是为了防止并联机构碰撞或损坏，将进一步保证运行过程中的安全性．此外，用户可查看关节运动随轨迹的变化曲线．

工作空间分析模块输入机器人的搜索边界和关节约束，输出为动平台的可达工作空间．

该软件基于B/S架构，采用Python的Flask框架进行开发，其功能架构如图10所示．

图10 软件架构

2.2 软件验证

[PP]S类机构[21]是一类含有3条PPS等效支链的1T2R并联机构，软件以本文所提出的方法为基础，将经典的10种[PP]S类机构的建模与分析过程数字化，本节以3-PRS机构为例说明软件的功能与有效性．

首先，在“机构”对话框中选择“PPS Class”和“Central Symmetry”选项，如图11所示．

式中：如果支链中沿静平台径向存在一个P关节，则，反之，则；和分别为动平台和静平台的半径；和分别为连杆1和连杆2的 长度．

1) 逆运动学求解

给定初始位姿和目标位姿分别为

自动计算得到的所有关节的逆运动学解如图12所示．

2) 轨迹仿真

给定初始位姿与逆运动学求解模块相同，关节和轨迹的约束为

当移动平台沿给定轨迹运动时，软件自动获取关节的运动轨迹并返回给用户，如图13所示．

3) 工作空间分析

输入搜索边界和约束

自动计算得到3-PRS并联机构期望运动的工作空间和伴随运动的工作空间如图14所示．

图12 逆运动学求解的计算结果

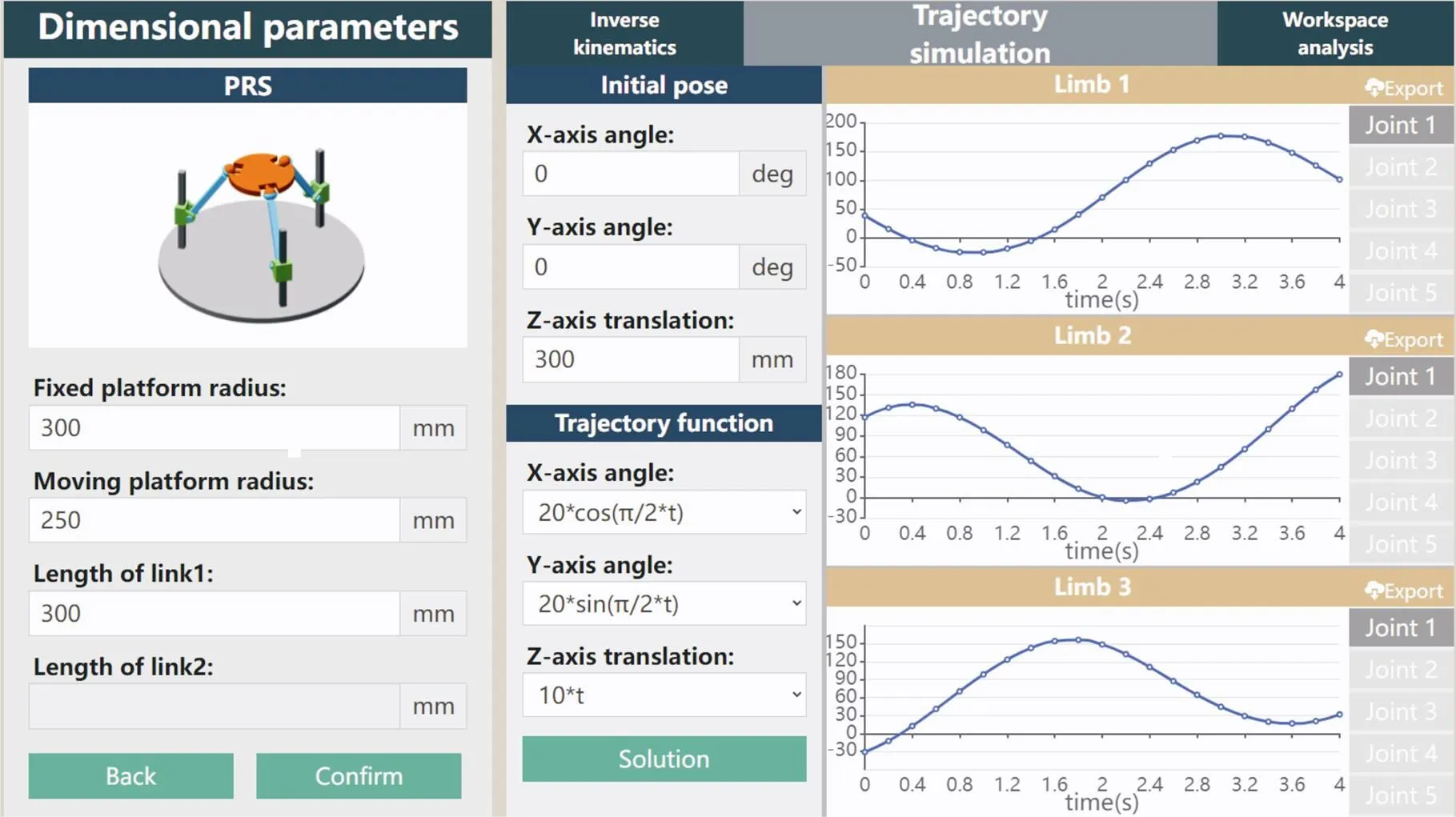
图13 轨迹仿真的计算结果

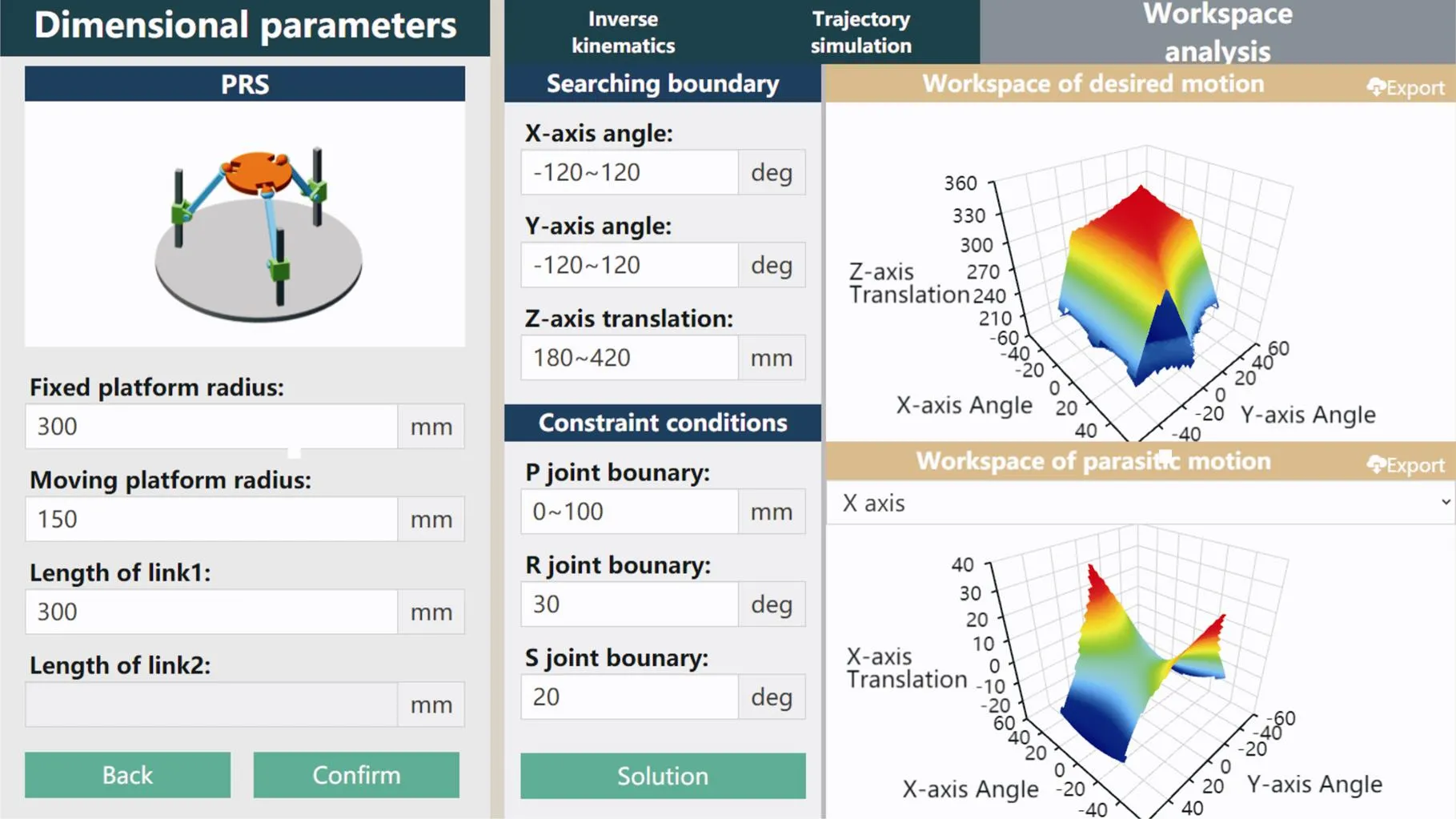
图14 工作空间分析的计算结果

3 讨 论

从适用性、计算成本和可编程性等角度对本文提出的基于有限旋量逆运动学分析方法与现有方法进行比较．

并联机构的逆运动学分析方法可以分为两类．一类是基于位移方程，主要利用关节和连杆之间的几何关系来建立矢量环路．一般地，该方法需要先求得驱动关节运动变量，然后利用更多的几何条件来求解其他变量．虽然采用易于求解的线性矢量方程提高了求解效率，但目前尚未有通用、系统的方法来构造几何条件和方程．因此，该方法较难应用于软件开发．另一类是基于运动方程的运动学分析方法，无需通过观察构造几何条件，主要方法包括D-H法、矩阵李群和对偶四元数，本文提出的方法也属于此种类型，该类方法的核心是构造并求解运动方程．D-H法和对偶四元数分别使用了12个和8个参数描述刚体运动，其中包含了部分被重复使用的参数，冗余参数将会提高分析和数值计算成本．而有限旋量使用6个元素，被认为是最紧凑的连续运动表达形式，因此，本文提出的方法能够以一种通用而简洁的方式解决逆运动学问题．此外，有限旋量的代数特征和易于数值计算的特点使得该方法特别适用于软件开发．

闭环矢量法、D-H法和有限旋量法之间的差异如表1所示．以UPS支链为例，在运动学求解中可以建立从U到S关节的闭环矢量，得到位移方程．首先求解P关节的变量和方向，由于方程不包括所有运动变量，因此通过添加几何条件来求解其他关节变量．应用D-H法则需要建立6个移动参考系，每个齐次矩阵有12个元素，方程数量多于运动变量，需要筛选方程．相比之下，有限旋量建立的方程包含6个元素和所有运动变量，可以直接求解．

表1 3种方法的比较

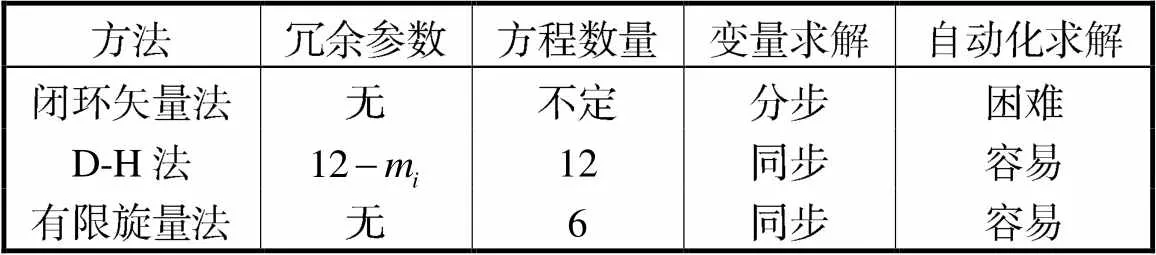
Tab.1 Comparison among three methods

基于有限旋量的方法由于方程是通过旋量三角积这一非线性运算求得，所以不易得到解析解，但与此同时，其在逆运动学建模中涉及最少的变量和方程，使得其在数值求解上较为方便，为开展并联机构全关节逆运动学分析数字化软件研发奠定了理论 基础．

4 结 论

针对现有并联机构逆运动学求解方法依赖观察和经验、存在冗余方程、难以实现数字化等不足，本文提出了一类基于有限旋量的并联机构全关节逆运动学求解方法，并研发了数字化逆运动学分析软件，全文结论总结如下．

(1) 提出了一种求解并联机构全关节运动学变量的方法，涉及机构初始化、运动学建模和运动学变量求解．为了方便获取关节轴线，在机构初始化中定义了虚拟位姿．基于有限旋量的简洁格式，可以在不观察几何条件的情况下列写运动学方程，以数值法对运动学方程进行求解，有效地得到所有关节运动变量．以一类两自由度并联机构为例，对所提方法进行了说明和验证．

(2) 将理论方法与计算机技术相结合，开发出适用于并联机构全关节逆运动学分析的数字化软件，功能模块包括逆运动学求解、轨迹仿真和工作空间分析，以3-PRS为例验证了软件的有效性．

(3) 讨论了本方法与基于向量和基于矩阵的方法的优缺点，本文所提的方法在标准化和自动化的建模求解中有较大的优势，有利于编程实现数字化的建模求解．

［1］ 王国锋，曹增欢，冯海生，等. 基于多阶段退化建模的谐波减速器实时可靠性评估与寿命预测[J]. 天津大学学报(自然科学与工程技术版)，2022，55(2)：122-132.

Wang Guofeng，Cao Zenghuan，Feng Haisheng，et al. Real-time reliability evaluation and life prediction of harmonic reducer based on multistage degradation mod-eling[J]. Journal of Tianjin University(Science and Technology)，2022，55(2)：122-132(in Chinese).

［2］ Sun T，Lian B. Stiffness and mass optimization of parallel kinematic machine[J]. Mechanism and Machine Theory，2018，120：73-88.

［3］ Merlet J P. Parallel Robots[M]. The Netherlands：Springer Science & Business Media，2006.

［4］ 于靖军. 机器人机构学的数学基础[M]. 北京：机械工业出版社，2008.

Yu Jingjun. The Mathematical Basis of Robot Mecha-nism[M]. Beijing：Machinery Industry Press，2008(in Chinese).

［5］ 宋轶民，贾殿魁，贺志远，等. 一种并联骨折手术机器人的安全运动控制方法[J]. 天津大学学报(自然科学与工程技术版)，2023，56(3)：221-231.

Song Yimin，Jia Diankui，He Zhiyuan，et al. Safety motion control for a parallel fracture surgical robot[J]. Journal of Tianjin University(Science and Technology)，2023，56(3)：221-231(in Chinese).

［6］ 黄 真，赵永生，赵铁石. 高等空间机构学[M]. 北京：高等教育出版社，2006.

Huang Zhen，Zhao Yongsheng，Zhao Tieshi. Advanced Spatial Mechanism[M]. Beijing：Higher Education Press，2006(in Chinese).

［7］ Spong M W，Hutchinson S，Vidyasagar M. Robot Modeling and Control[M]. New York：Wiley，2006.

［8］ Wang Y，Belzile B，Angeles J，et al. Kinematic analy-sis and optimum design of a novel 2PUR-2RPU parallel robot[J]. Mechanism and Machine Theory，2019，139：407-423.

［9］ Yang A T，Ferdinand F. Application of dual-number quaternion algebra to the analysis of spatial mecha-nisms[J]. Journal of Applied Mechanics，1964，31(2)：300.

［10］ Aspragathos N A，Dimitros J K. A comparative study of three methods for robot kinematics[J]. IEEE Transac-tions on Systems，Man，and Cybernetics，1998，28(2)：135-145.

［11］ Gosselin C M. Simulation and computer-aided kinematic design of three-degree-of-freedom spherical parallel manipulators[J]. Journal of Field Robotics，2010，12(12)：857-869.

［12］ Kucuk S. Simulation and design tool for performance analysis of planar parallel manipulators[J]. Simulation，2012，88(5)：542-556.

［13］ Inner B，Kucuk S. A novel kinematic design，analysis and simulation tool for general Stewart platforms[J]. Simulation，2013，89(7)：876-897.

［14］ Gil A，Peidro A，Reinoso O，et al. Implementation and assessment of a virtual laboratory of parallel robots developed for engineering students[J]. IEEE Transactions on Education，2017，57(2)：92-98.

［15］ Sun T，Yang S，Lian B. Finite and Instantaneous Screw Theory in Robotic Mechanism[M]. Singapore：Springer，2020.

［16］ 王 蕊，霍欣明，连宾宾，等. 面向骨折手术的三支链六自由度并联机构设计[J]. 天津大学学报(自然科学与工程技术版)，2022，55(3)：273-282.

Wang Rui，Huo Xinming，Lian Binbin，et al. Developing three-legged six-degree-of-freedom parallel mechanism for bone reduction surgery[J]. Journal of Tianjin University(Science and Technology)，2022，55(3)：273-282(in Chinese).

［17］ Dai J S. Euler-Rodrigues formula variations，quaternion conjugation and intrinsic connections[J]. Mechanism and Machine Theory，2015，92：144-152.

［18］ Klein F. A comparative review of recent researches in geometry[J]. Bulletin of the American Mathematical Society，1893，2(10)：215-249.

［19］ Qi Y，Song Y. Coupled kinematic and dynamic analysis of parallel mechanism flying in space[J]. Mechanism and Machine Theory，2018，124：104-117.

［20］ Rocha C R，Tonetto C P，Dias A. A comparison between the Denavit-Hartenberg and the screw-based methods used in kinematic modeling of robot manipulators[J]. Robotics and Computer-Integrated Manufacturing，2011，27(4)：723-728.

［21］ Li Q，Chen Z，Chen Q，et al. Parasitic motion comparison of 3-PRS parallel mechanism with different limb arrangements[J]. Robotics and Computer-Integrated Manufacturing，2011，27(2)：389-396.

An Approach for Inverse Kinematics Analysis of Full Joint of Parallel Mechanism

Sun Tao1，Wang Liang1，Huo Xinming1，Qi Yang2，Wang Jun3，Li Qi3

(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300350，China；2. School of Mechanical Engineering，Tianjin University of Technology and Education，Tianjin 300222，China；3. Tianjin Key Laboratory of Aerospace Intelligent Equipment Technology，Tianjin Institute of Aerospace Mechanical and Electrical Equipment，Tianjin 300301，China)

Inverse robotic kinematics is the basis of performance modeling and design. Current methods always focus on the mapping between actuator and manipulator spaces. However，for the passive joint，iterative eliminations are based on geometric characteristics. Therefore，the construction of an algebraic solution process and digital analysis software is difficult. To solve the aforementioned problems，an inverse solving method for full joint displacements of the parallel robotic mechanism is proposed by employing the finite screw and developing its digital software in this study. First，the procedure for obtaining the full joint position solution of the parallel mechanism is presented. The initial poses of the end of the parallel mechanism and its branches are constructed. Equations of motions are first established in the format of the finite screw and then solved numerically. Taking the 4RSR-SS parallel robot with two rotational motions as an example，the full joint displacement variables of each limb are calculated and compared with the simulation results to verify the accuracy of the solutions. Then，the digital algorithm for full joint displacements is established，and the inverse kinematics analysis software for parallel mechanisms is developed based on the B/S architecture，including inverse kinematics，trajectory simulation，and workspace analysis modules. The software is verified by analyzing the kinematics of the 3-PRS parallel mechanism. Finally，comparisons with the existing methods in terms of redundant parameters and number of equations are made. The advantages of the fully joint inverse kinematics analysis method proposed in this study are as follows：kinematic equations can be expressed in a general and concise manner；full joint variables under the given target pose could be solved by a single step instead of iterations；it is conducive to programming，which helps realize the digitalization of inverse kinematics analysis.

inverse kinematics；parallel mechanism；finite screw；digitalization；kinematics analysis software

10.11784/tdxbz202206033

TH112

A

0493-2137(2023)09-0942-11

2022-06-05；

2022-09-10.

孙 涛（1983— ），男，博士，教授，stao@tju.edu.cn.Email：m_bigm@tju.edu.cn

霍欣明，xmhuo@tju.edu.cn.

国家自然科学基金资助项目(62027812，51875391，51775367，51905378)；天津市科技计划资助项目(20201193，18PTLC-SY00080)；天津市自然科学基金资助项目(20JCQNJC00360)；天津市技术创新引导专项基金企业科技特派员项目(20YDT-PJC00450)；天津市航天智能装备技术重点实验室开放项目(TJYHZN2019KT002)；天津大学机构理论与装备设计教育部重点实验室开放基金资助项目．

the National Natural Science Foundation of China(No.62027812，No.51875391，No.51775367，No.51905378)，Tianjin Science and Technology Plan Project(No.20201193，No.18PTLCSY00080)，the Natural Science Foundation of Tianjin，China(No.20JCQNJC00360)，Tianjin Technology Innovation Guidance Special Fund Enterprise Science and Technology Specialists Project(No.20YDTPJC00450)，the Open Project Program of Tianjin Key Laboratory of Aerospace Intelligent Equipment Technology(No.TJYHZN2019KT002)，the Open Fund of the Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education of Tianjin University.

(责任编辑：王晓燕)