柔性关节的复合动态面控制仿真研究

洪 鹰，李辉鹭，肖聚亮，刘海涛

柔性关节的复合动态面控制仿真研究

洪 鹰，李辉鹭，肖聚亮，刘海涛

(天津大学机构理论与装备设计教育部重点实验室，天津 300350)

针对柔性关节机械臂轨迹跟踪控制中存在参数不确定性、建模误差和未知扰动等问题，为了保证柔性关节系统的控制精度，在建立其等效动力学模型的基础上，提出了一种新的复合动态面控制策略．该策略包含动态面控制技术、参数自适应算法、神经网络逼近器、鲁棒补偿器以及约束处理方案．首先，利用动态面控制技术进行控制器的设计，消除了反步法的“复杂性爆炸”问题．其次，采用参数自适应算法处理柔性关节系统动力学模型中的参数不确定性，神经网络逼近器用于在线逼近和补偿模型中的不连续摩擦、建模误差和未知扰动，鲁棒补偿器负责前两部分的残余误差，同时设计约束处理方案满足误差规定性能约束和提高控制器对神经网络近似误差和未知扰动的鲁棒性．再次，构建具有预测误差的复合学习自适应律，提高控制器对模型不确定项的补偿精度．李雅普诺夫稳定性分析表明，所提出的策略保证了闭环系统中的所有信号都是半全局一致最终有界的，跟踪误差最终以规定性能收敛到零附近的一个小邻域．最后，在Simulink环境中，基于单连杆柔性关节系统对该控制策略进行对比仿真验证，结果表明：该复合动态面控制策略能够显著提高柔性关节系统的跟踪性能并降低其超调量和稳定时间，验证了该复合动态面控制策略的有效性和优越性．

柔性关节；动态面控制；神经网络；自适应鲁棒控制；复合学习

近年来，柔性关节机械臂由于其重量轻、能耗低、负载自重比高、操作安全等[1-2]优点，在实际工程中起到十分重要的作用．因此，柔性关节机械臂的轨迹跟踪控制问题引起了广泛的关注．然而严重的非线性、参数不确定性、关节柔性引起的耦合以及外部扰动使得柔性关节系统的建模和控制变得特别困难[1,3].为了保证柔性关节系统的轨迹跟踪精度，已经有大量文献进行了研究．Le-Tien等[4]提出了一种基于级联结构的自适应鲁棒控制方案，精确补偿了柔性关节机械臂中的参数或结构化(也称为建模)不确定性，获得了较好的跟踪性能．然而，柔性关节系统存在高非线性的不连续摩擦力、弹性力矩、未建模动力学以及未知时变扰动等非结构化不确定性，而自适应鲁棒控制无法精确补偿非结构化不确定性[5]．

缓解上述问题的有效方法是神经网络控制，其作为通用逼近器具有强大的非线性映射能力．例如，Liu等[6]结合神经网络和动态面控制技术，考虑了具有不确定性的柔性关节机器人系统的轨迹跟踪控制问题．Wang等[7]利用约束变换函数和神经网络，设计了一种具有未知动力学和输出跟踪误差约束的柔性关节机械手的自适应神经网络控制器．但对于不连续摩擦和未知时变扰动，神经网络控制不能保证良好的逼近结果[8-9]．针对上述问题的有效解决方案是结合自适应鲁棒控制和神经网络的复合控制策略．该策略利用神经网络的非线性逼近能力进一步提高自适应鲁棒控制的性能与系统的抗干扰性能．Wang等[5]合成了一种神经网络学习自适应鲁棒控制器，在利用参数自适应算法对线性参数不确定性进行补偿的基础上，通过神经网络逼近未建模项和扰动，使直线电机具有良好的跟踪性能和抗扰动能力．

另外，目前应用神经网络等智能算法或参数自适应算法补偿柔性关节系统的模型不确定项时，主要依赖于跟踪误差去设计自适应律，没有充分考虑它们近似模型不确定项的最初意图，从而降低了算法对模型不确定项的补偿精度[10]．为了提高控制器对模型不确定项的补偿效果，Xu[11]通过具有预测误差的复合学习算法，提高了神经网络对柔性连杆机械臂不确定性的逼近精度和扰动观测器对扰动的估计能力．

虽然上述方法可以保证良好的轨迹跟踪效果，但是在某些场合下，不仅要保证柔性关节系统的轨迹跟踪精度，还要使其输出误差满足规定性能约束．目前在柔性关节系统的输出约束上主要采用障碍李雅普诺夫函数(barrier Lyapunov function，BLF)[12]或规定性能约束(prescribed performance constraint，PPC)[13]来实现输出误差的受限．然而相比PPC，BLF无法充分考虑误差的最大超调量和收敛速度要求．此外，PPC可以降低初始控制输入幅度[14]．同时，考虑输出误差约束还可以提高系统对未知扰动的鲁棒性[15]．

在上述研究工作的启发下，为进一步提高柔性关节系统的轨迹跟踪精度和扰动抑制能力，笔者首先建立柔性关节系统的动力学模型．然后基于动态面控制技术、PPC、参数自适应算法和神经网络，提出一种新的复合动态面控制策略．该策略在利用动态面控制技术实现柔性关节系统稳定控制的基础上，采用参数自适应算法和径向基函数(radial basis function，RBF)神经网络逼近器来在线补偿模型不确定项，且构造鲁棒补偿器负责前两部分的残余误差；同时设计约束处理方案满足误差规定性能约束和进一步提高控制器的抗扰动能力；此外利用预测误差形成新的复合自适应律，提高控制器对模型不确定项的逼近效果．通过李雅普诺夫理论证明了整个控制系统的稳定性．最后为了验证该控制策略的有效性，本文基于单连杆柔性关节系统对该控制策略进行了对比仿真．结果表明，该策略能够显著提高柔性关节系统的动态特性、轨迹跟踪精度以及抗扰动能力．

1 动力学建模

单连杆柔性关节系统的结构如图1所示．

单连杆柔性关节系统的动力学模型通常包含刚性连杆动力学和电机动力学，可通过拉格朗日公式描述[16]，即

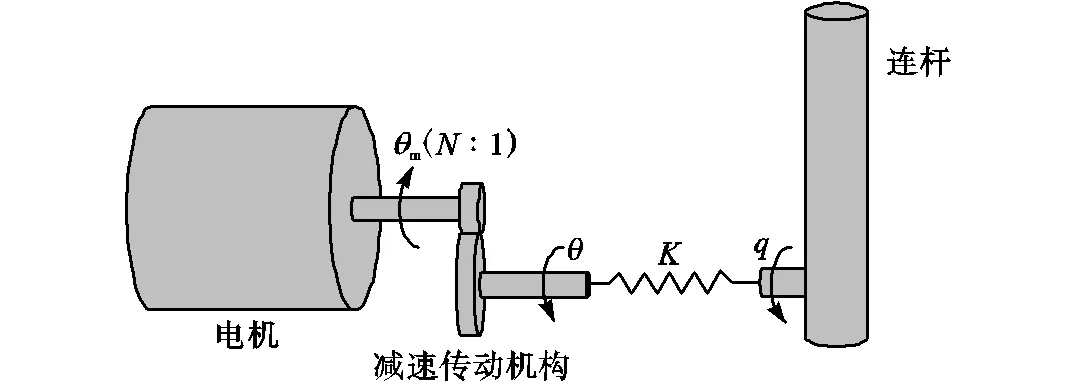
图1 单连杆柔性关节系统结构

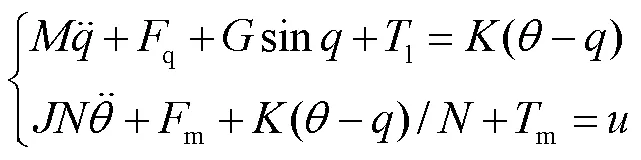
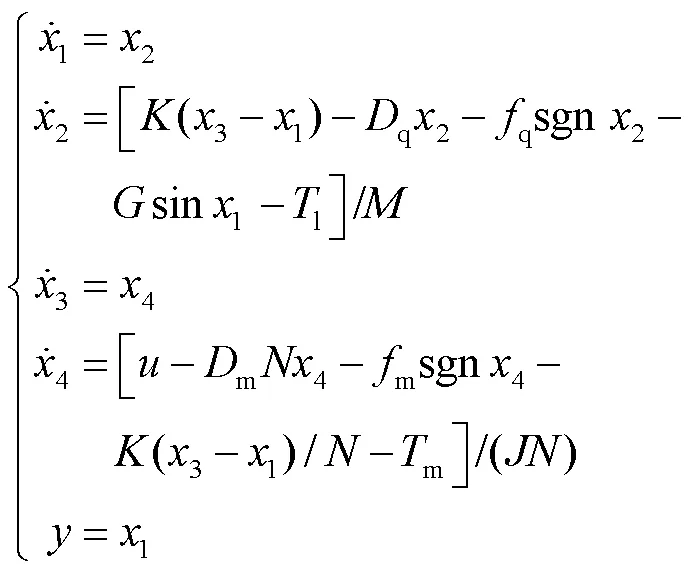
为了便于控制器的设计，需要假设所有状态变量均可得到用于反馈[17]．

2 控制器设计和稳定性分析

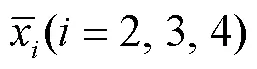
2.1 控制器设计

在控制器设计之前，先定义误差变量，即

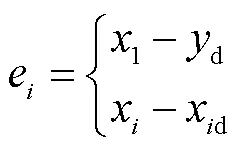
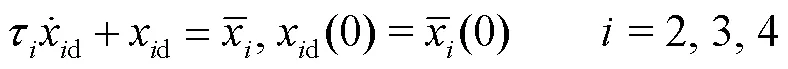
相应的滤波误差为

为了保证跟踪误差快速收敛，并达到一定的收敛精度，跟踪误差按式(6)进行设定．

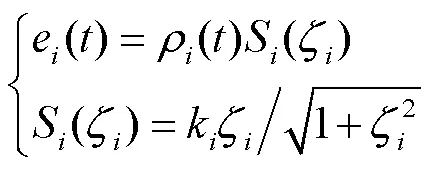
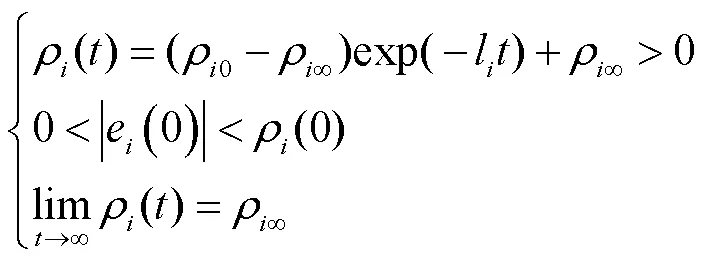
由式(6)、(7)可知，如果下列条件成立，则跟踪误差满足规定性能约束且方便后续设计约束处理方案提高系统对未知扰动的鲁棒性[13, 15]．

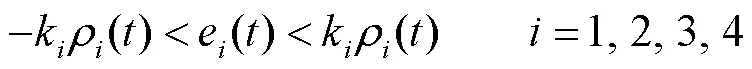
则等效无约束跟踪误差可描述为

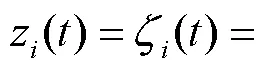
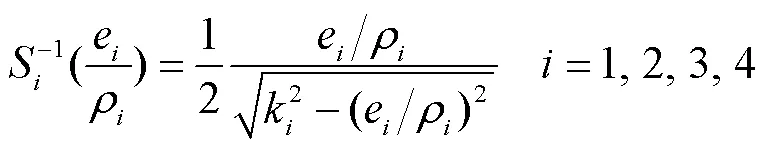
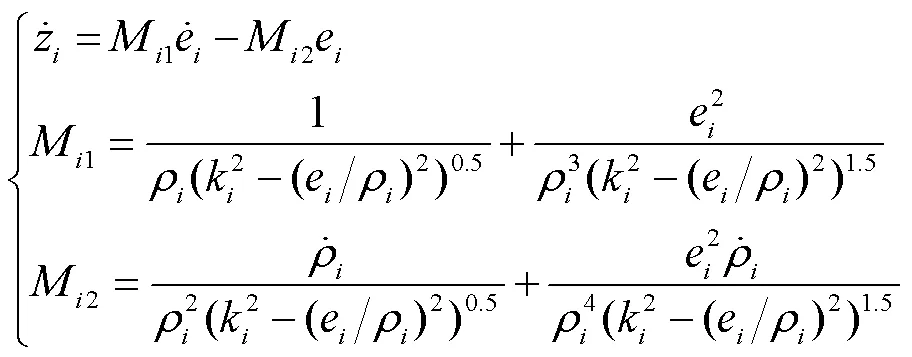
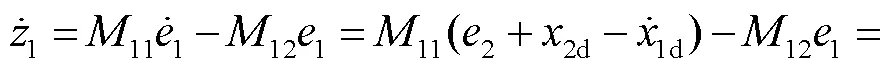
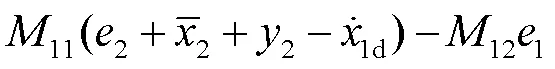
商景兰(1605—1676)，字媚生，浙江山阴(今绍兴)人。明朝吏部尚书商周祚长女，与妹商景徽皆有国色而能诗。商景兰16岁嫁与藏书家祁承烨之子祁彪佳为妻，二人以“金童玉女”的佳配被传为美谈。祁彪佳终身未纳妾媵，伉俪相重，世所罕见。顺治二年乙酉(1645)，清兵攻陷南京，祁彪佳自沉殉节，商景兰遵丈夫遗命接掌家业，并带领家族女性从事诗歌创作，闺阁唱和，登临题咏，一时传为胜事。后女祁德琼、子祁班孙先后离世，商景兰死后，祁氏一门风雅亦随家族破败而沦没。现存《锦囊集》，附于《祁彪佳集》之后。

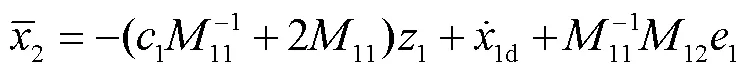
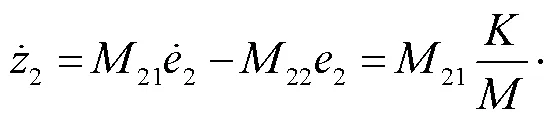
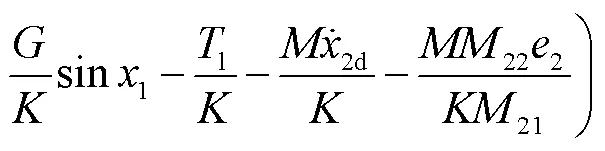
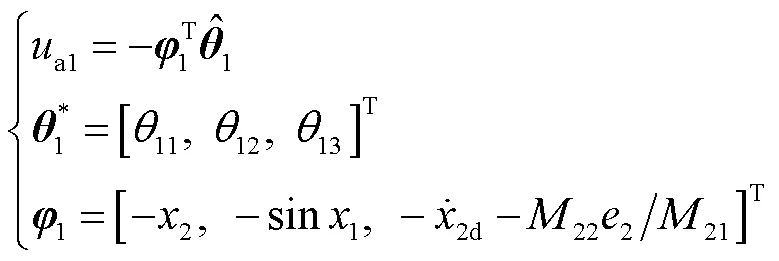
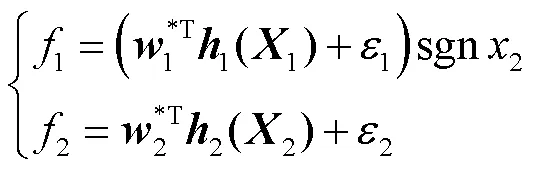
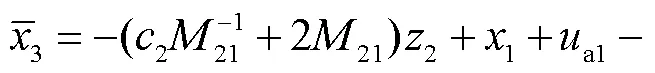
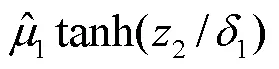
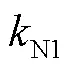
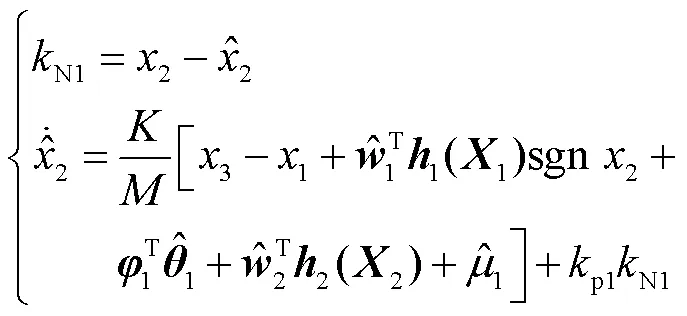
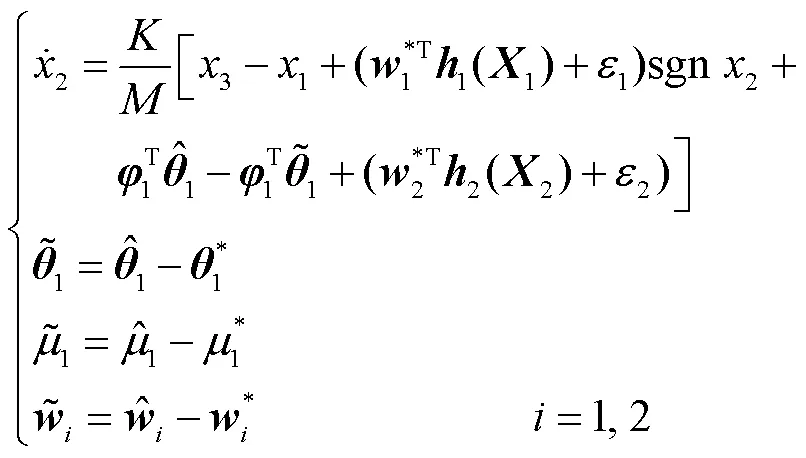
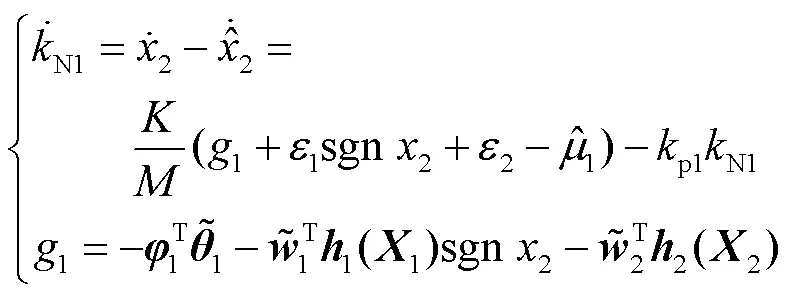
随后结合预测误差设计复合学习自适应律为

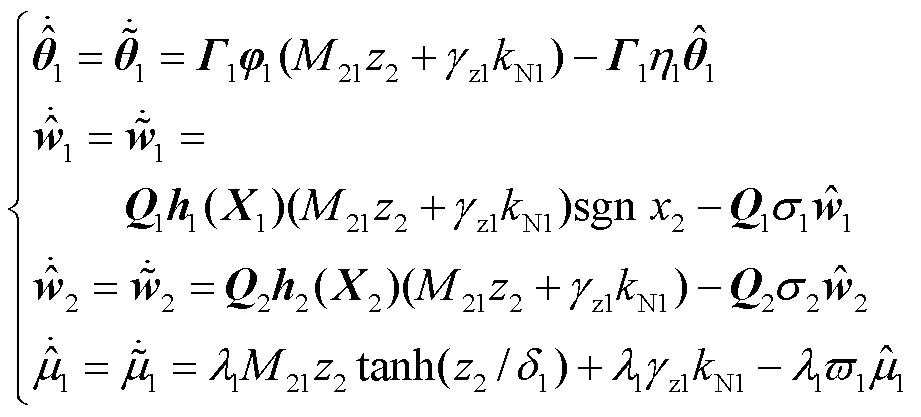
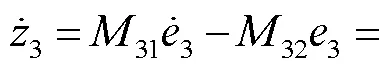
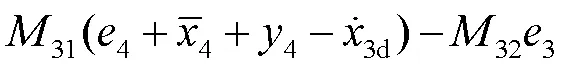
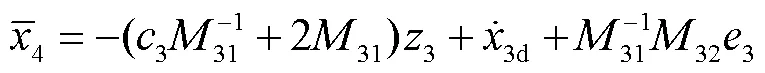
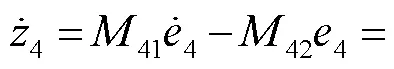
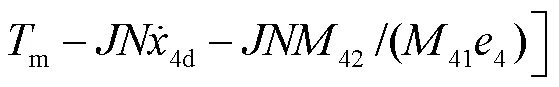
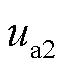
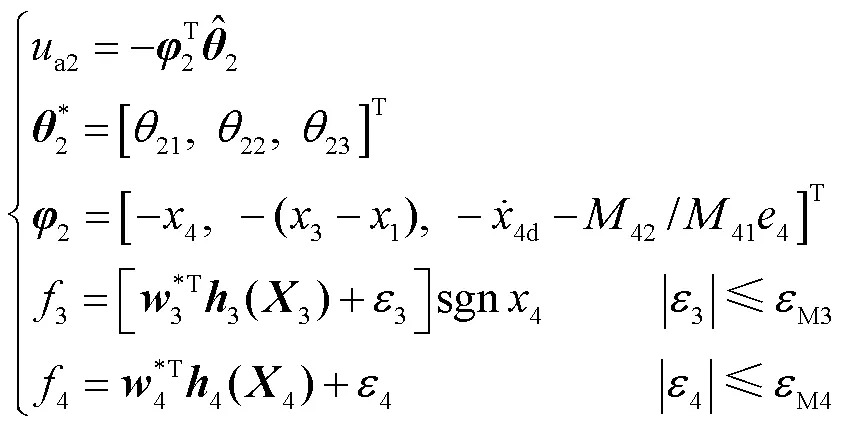
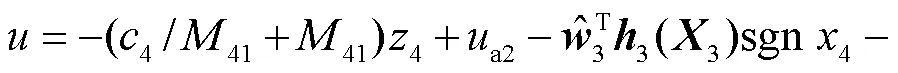
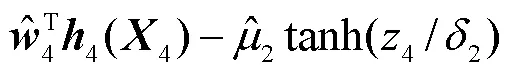
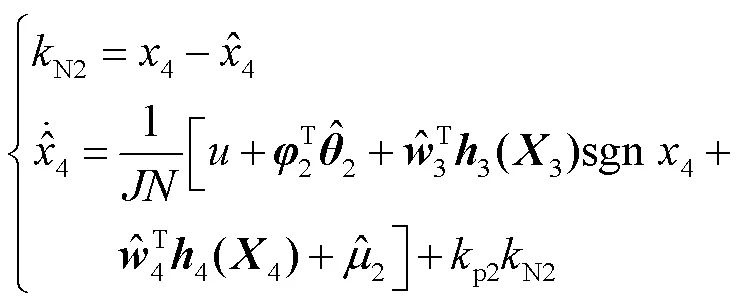
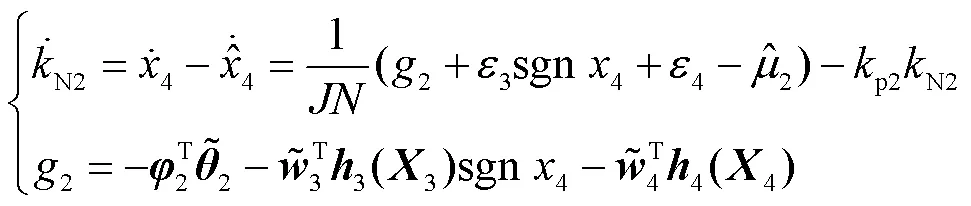
则结合预测误差设计复合学习自适应律为

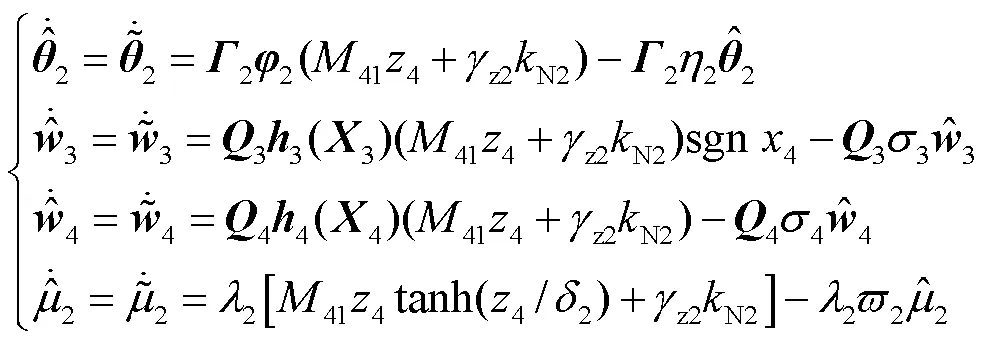
复合动态面控制策略的流程如图2所示．目前已经完成了整个控制器的设计，为了保证整个控制系统的稳定，下面进行稳定性分析．

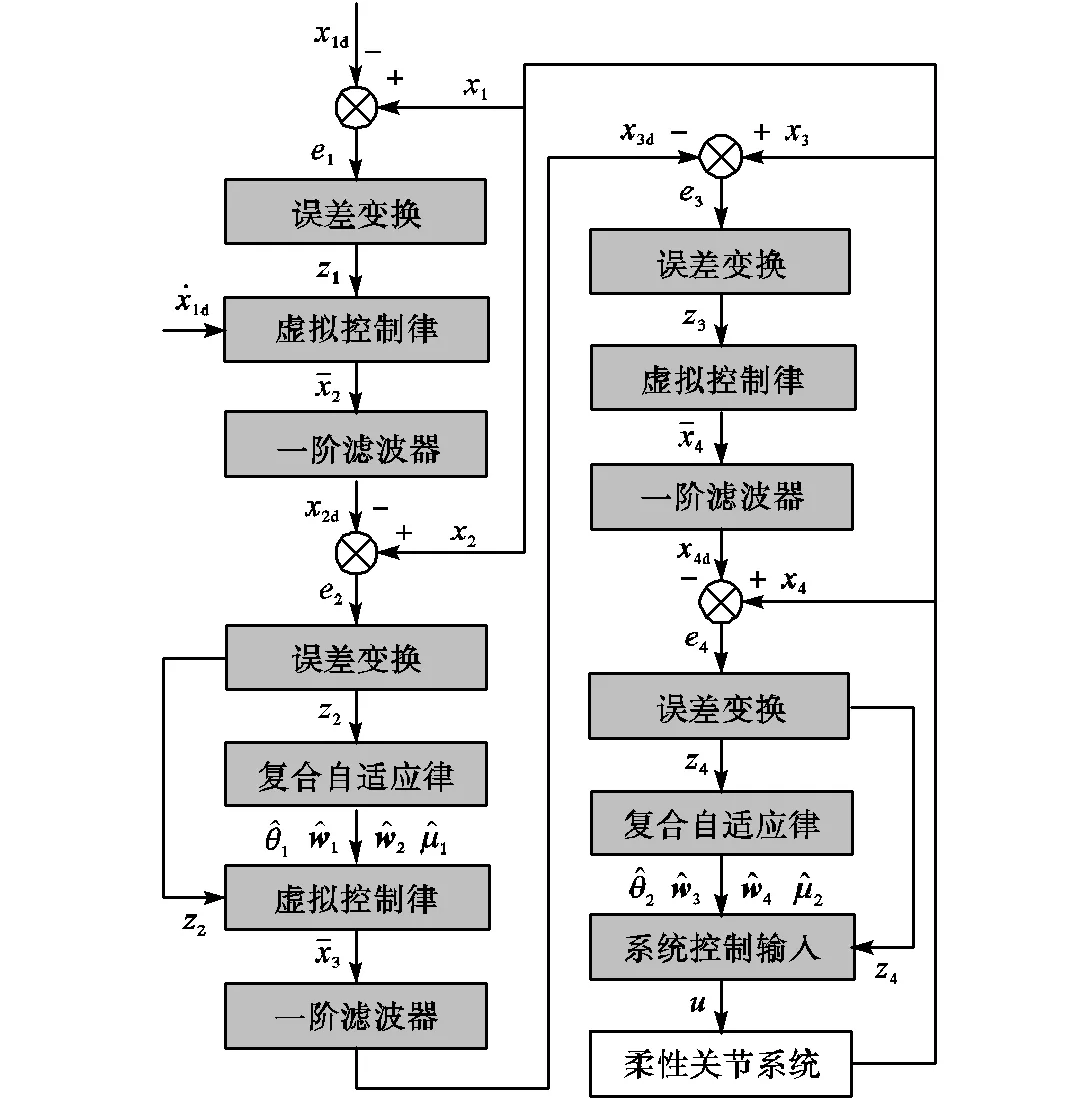
图2 柔性关节系统复合动态面控制流程

2.2 稳定性分析

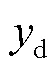
证明：选择李雅普诺夫函数为

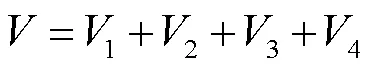
其中

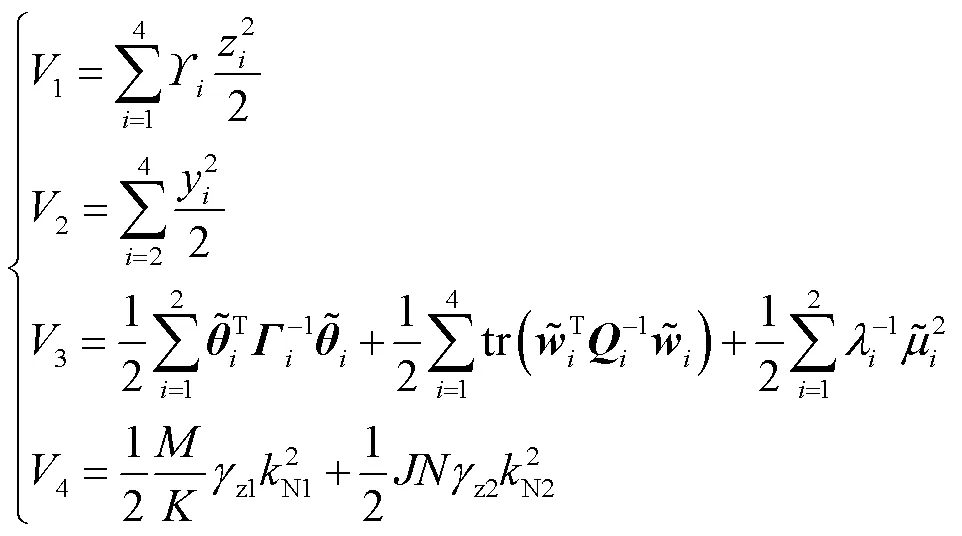
基于式(4)和式(5)，滤波误差的时间导数可以表示为

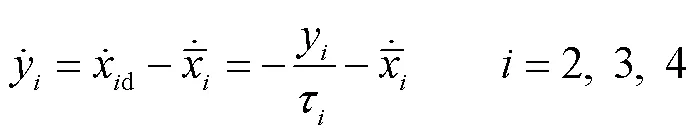
利用杨氏不等式可得

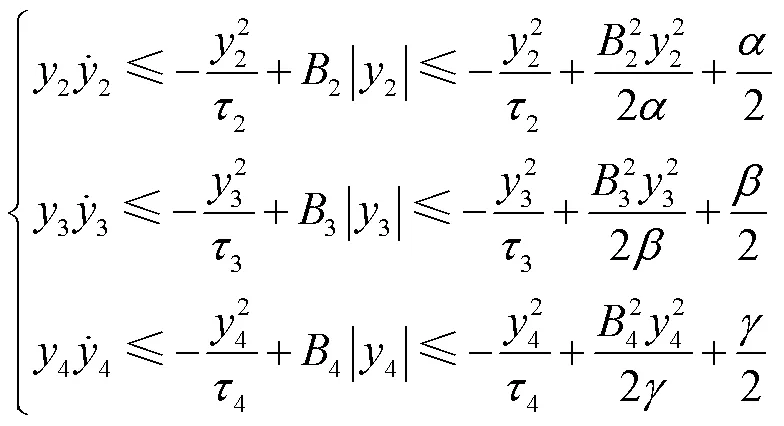
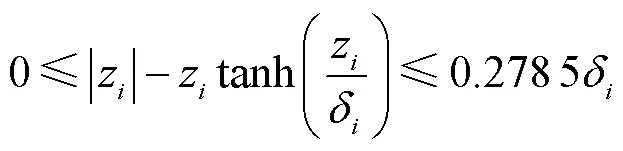
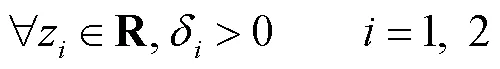
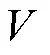
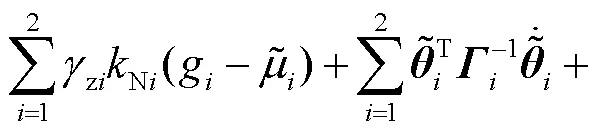
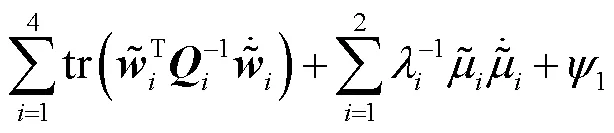
其中

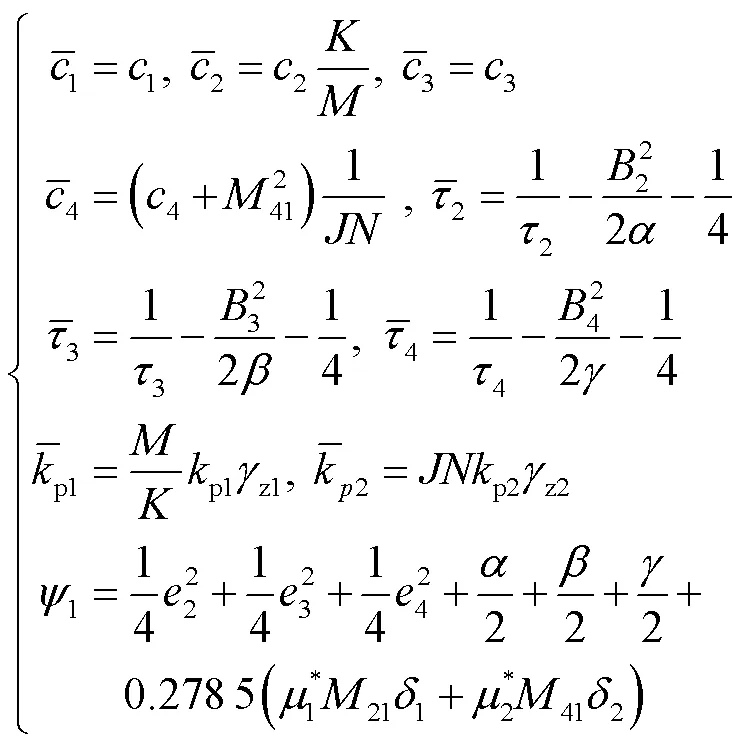
将式(20)、(29)代入式(35)得到

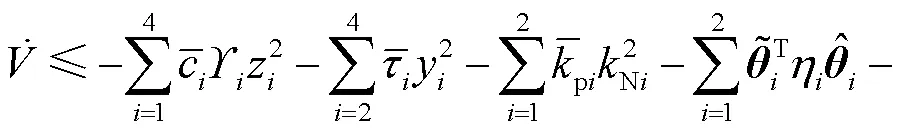
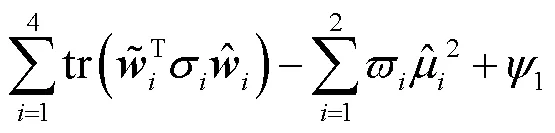
通过利用式(18)、(27)，可得

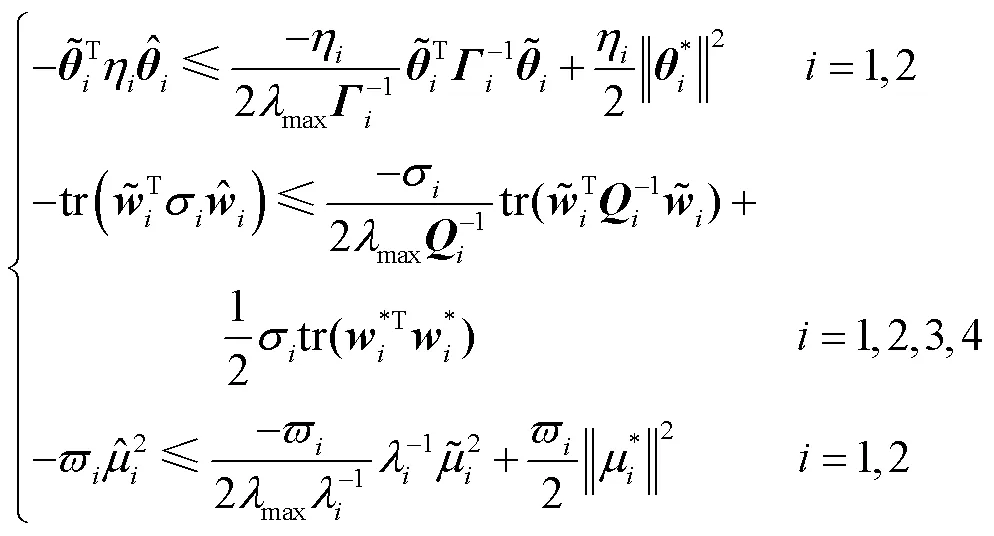
然后，选择以下设计参数以保证整个闭环系统的稳定性，即

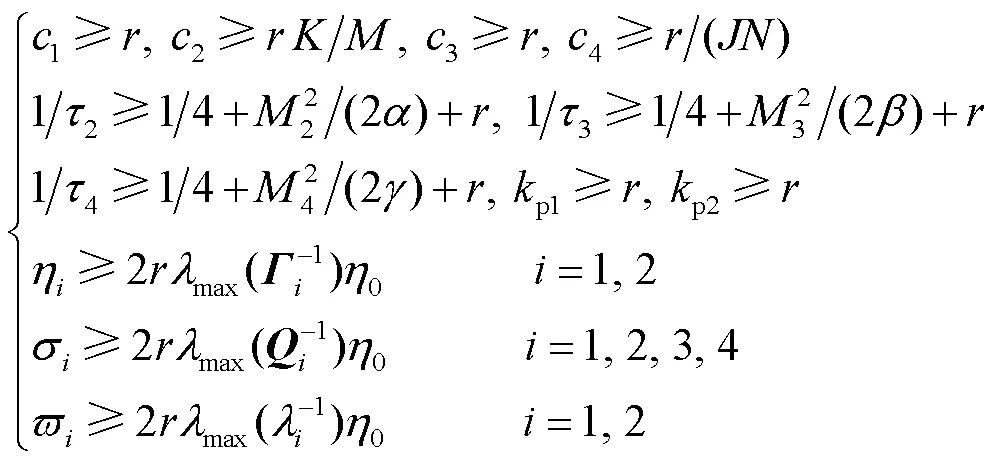
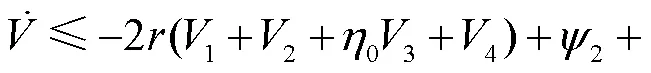
其中

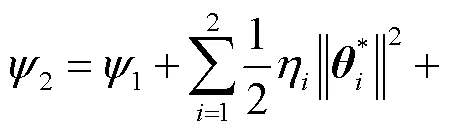
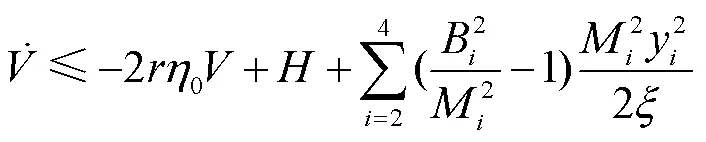
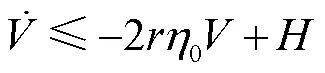
通过解式(42)的不等式得

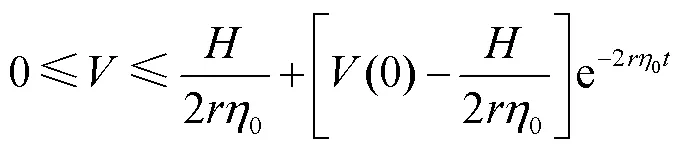
显然，闭环系统所有信号半全局一致最终有界，并且有

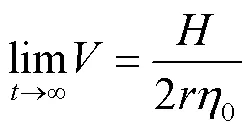
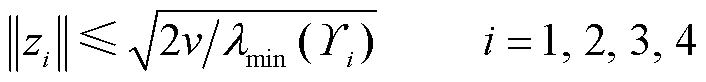
3 仿真验证

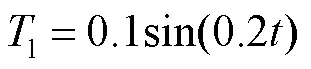
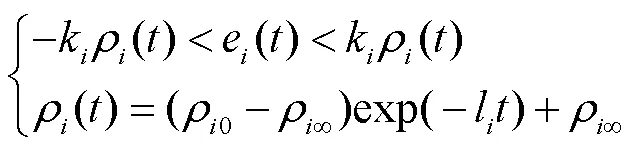
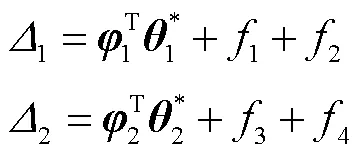
其中

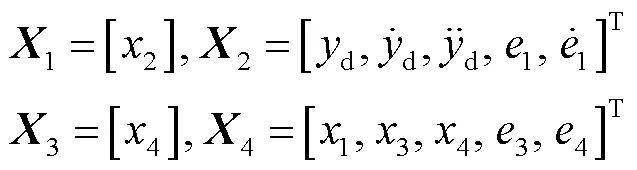
所选择的系统初始状态为

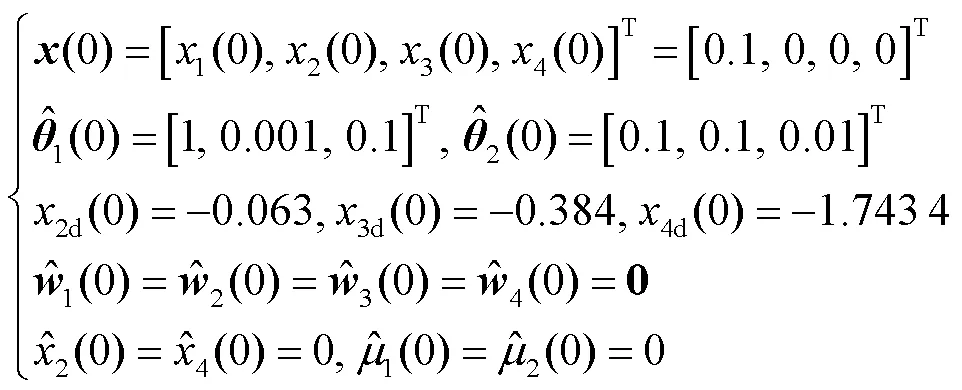
为了验证所提出的控制策略的有效性和优越性，本文将该策略与文献[6-7]中的控制策略进行比较．则定义策略1、策略2、策略3如下．

策略1：采用RBF神经网络逼近器的自适应动态面控制策略[6]．其虚拟控制律和控制输入力矩设计为

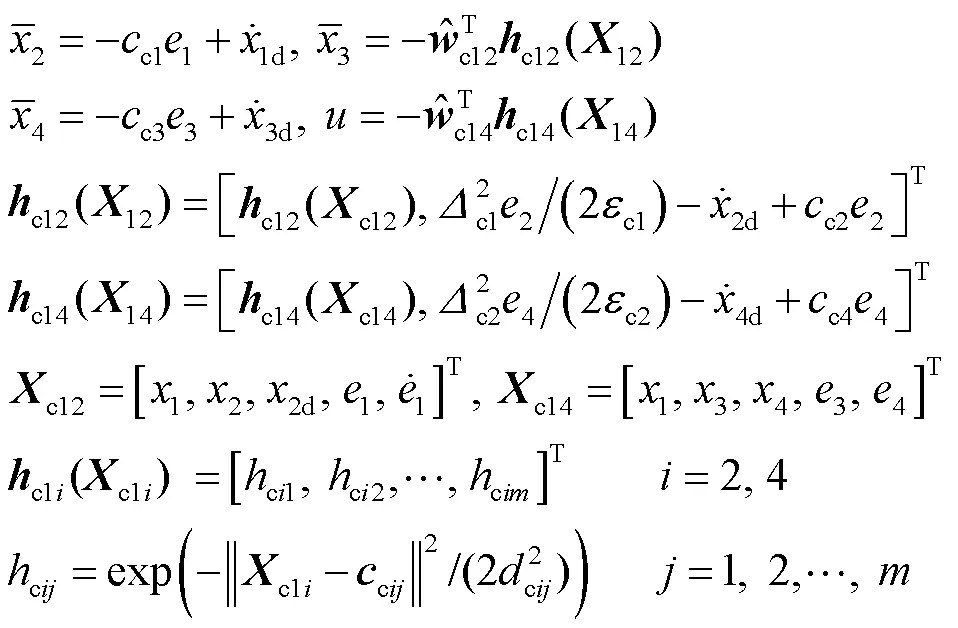
其中

对应的权值自适应律为

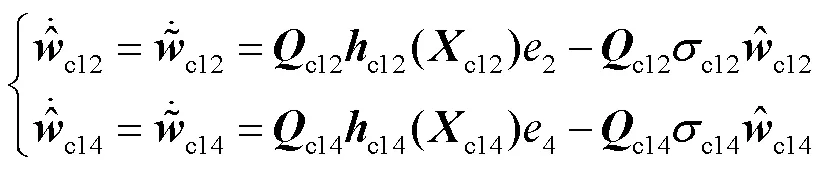
其中

策略2：具有规定性能约束的自适应神经网络动态面控制策略[7]．其虚拟控制律和控制输入力矩设 计为

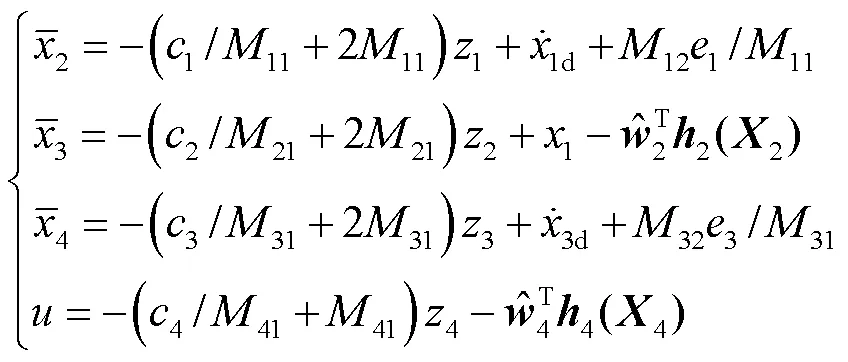
相应的权值自适应律为

策略3：复合动态面控制策略．

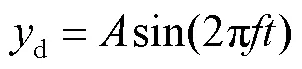
仿真结果如图3～图11所示．

表1 柔性关节系统动力学参数

Tab.1 Dynamic parameters of the flexible-joint system

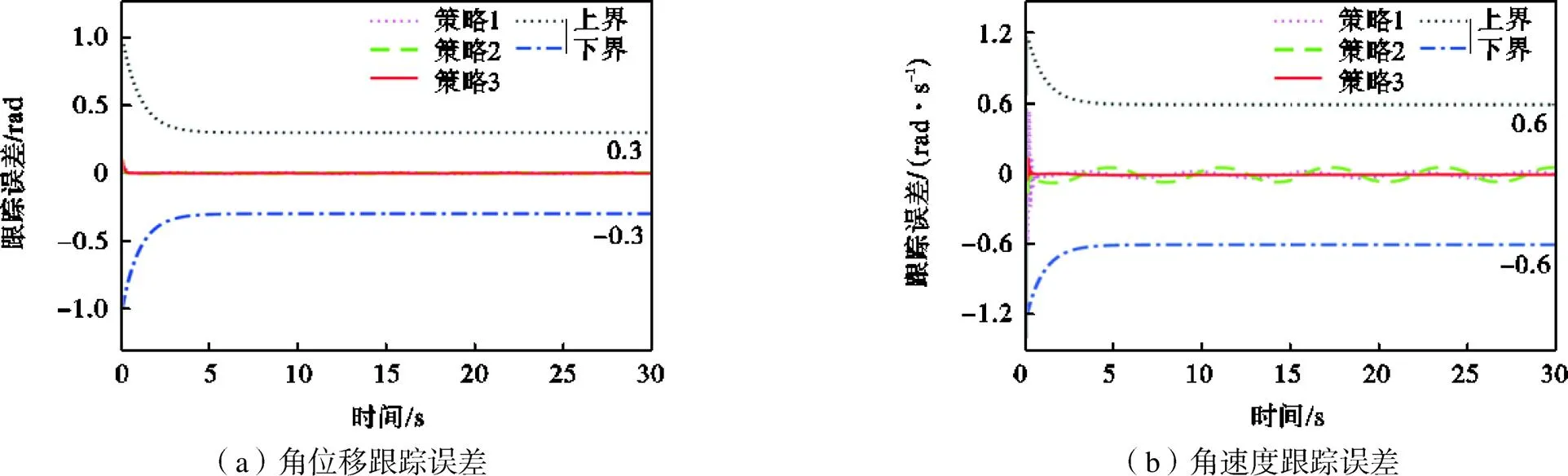
图3 具有规定性能的连杆侧跟踪误差曲线

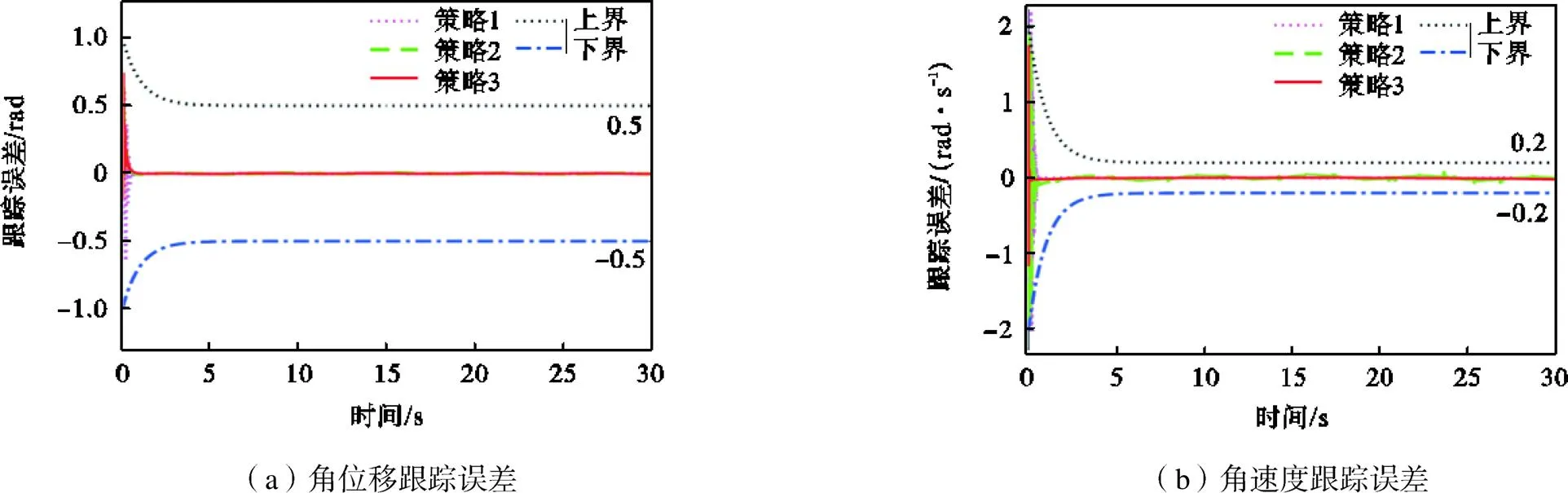
图4 具有规定性能的电机侧跟踪误差曲线

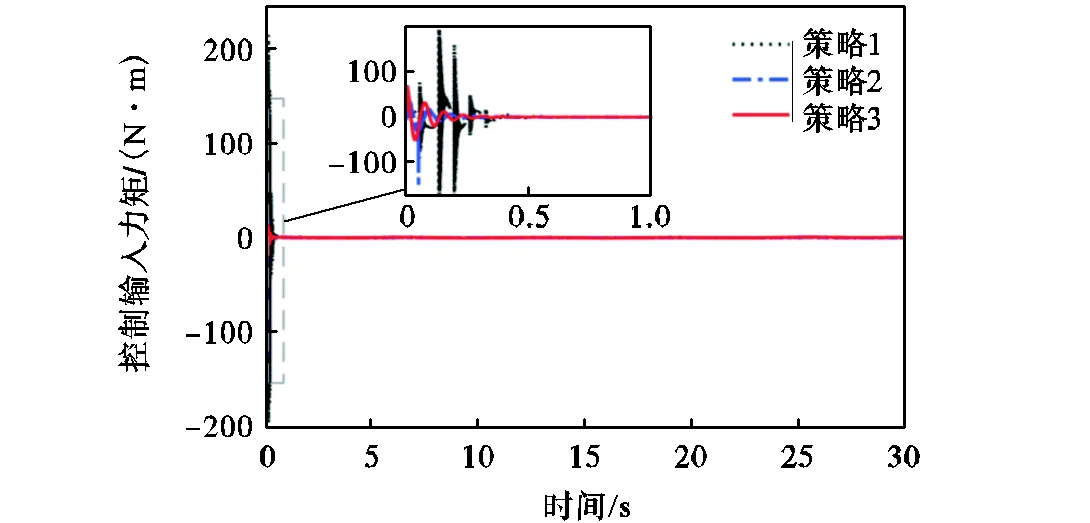
图5 3种控制策略下的控制输入曲线

图3和图4表明本文所提策略3的跟踪误差满足规定性能约束，且相比策略1、策略2，跟踪误差波动性较小．系统的控制输入如图5所示，可以看出所提出的策略3需要的初始控制输入力矩小于策略1和策略2．图6表示在正弦参考轨迹幅值为1rad，频率分别为1/(4π)Hz、1/π Hz的情况下，所提出的策略3的连杆侧轨迹跟踪效果．图7反映了正弦参考轨迹频率为1/(2π)Hz，幅值分别为0.5rad、0.8rad的情况下，策略3的连杆侧轨迹跟踪效果．图6和图7验证了本文所提出复合动态面控制策略的有效性．图8展示了连杆侧角位移跟踪曲线，从图8可以注意到3种控制策略都能达到令人满意的控制效果．图9表示连杆侧角位移跟踪误差(轨迹跟踪误差)，很好地说明了本文所提出策略的有效性和优越性，其中选择了最大跟踪误差和最大超调量的性能指标来比较柔性关节系统的跟踪性能．3种控制策略在稳态下的最大轨迹跟踪误差分别为0.00578rad(策略1)、0.00270rad (策略2)、0.00045rad(策略3)．另外，采用策略1、策略2和策略3的最大轨迹跟踪误差减少到稳态误差范围内所用时间分别为3.18s、4.75s、2.71s．

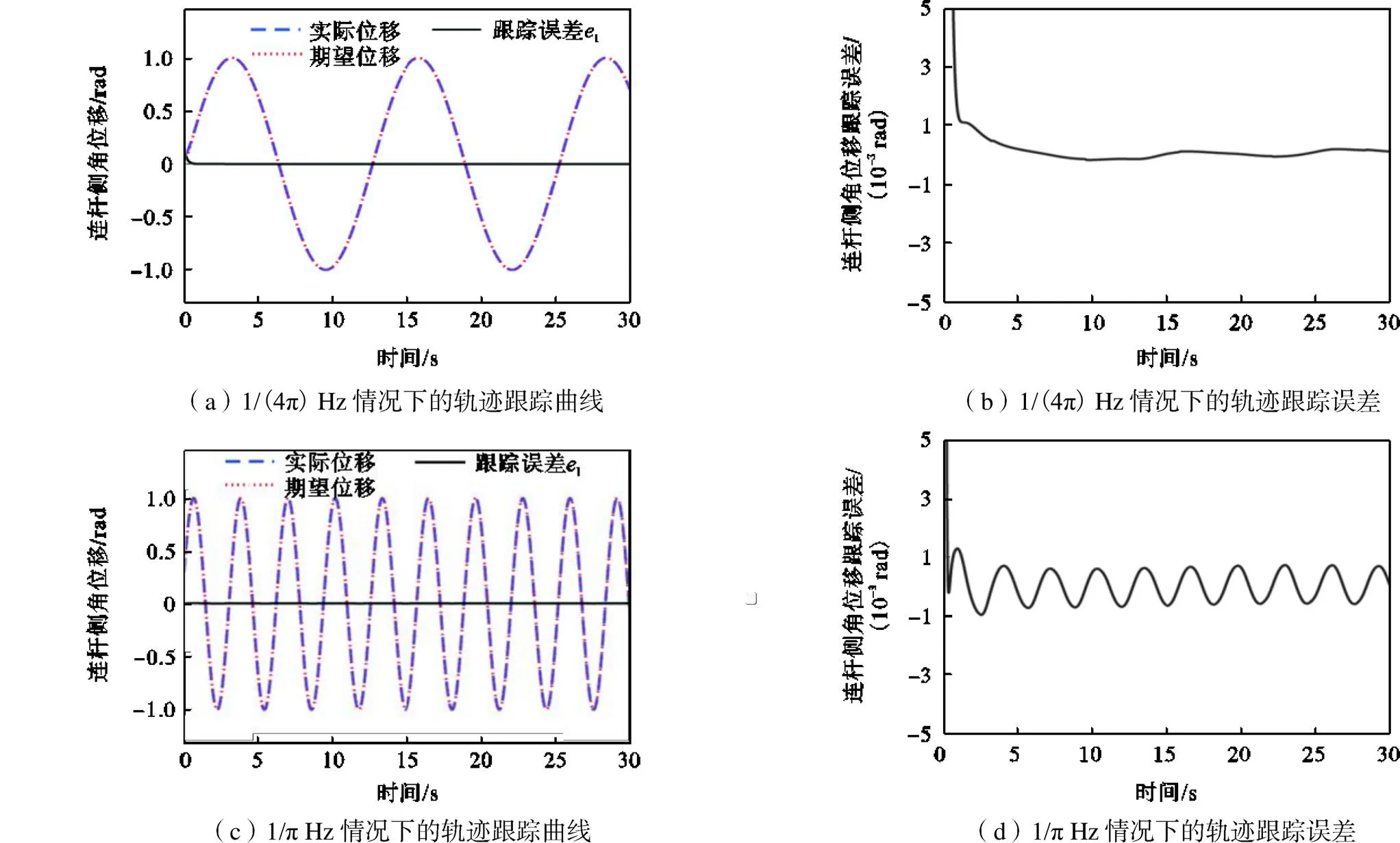
图6 不同频率下连杆侧轨迹跟踪曲线

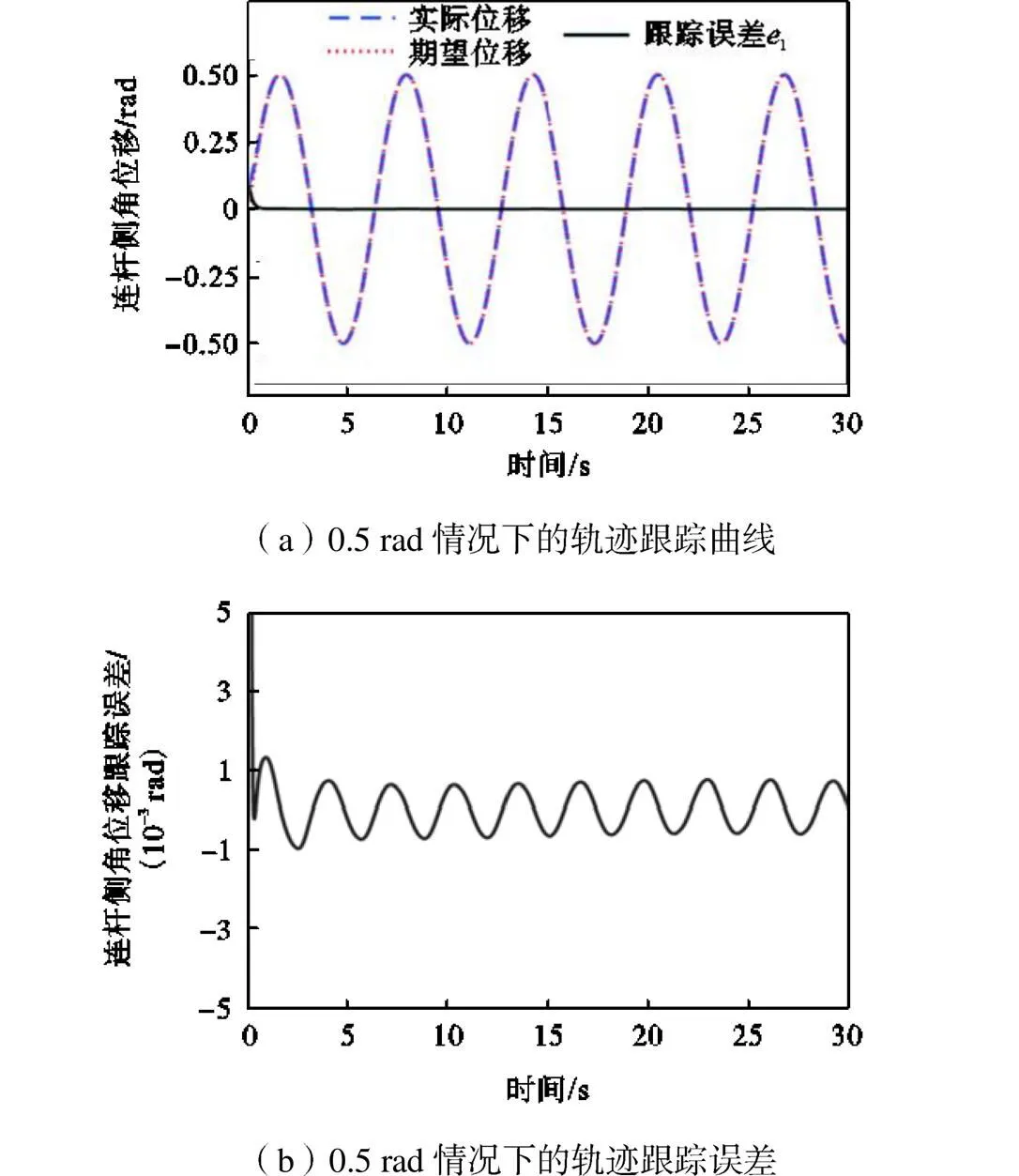
此外，3种控制策略轨迹跟踪误差的最大超调量分别为0.00583rad(策略1)、0.00466rad(策略2)和0.00119rad(策略3)．以上结果表明，本文所提出策略的轨迹跟踪误差避免了不必要的超调，减少了稳定时间，并在较短时间内以规定性能收敛到原点附近的一个足够小的邻域，且其稳态跟踪误差小于另外两种控制策略．

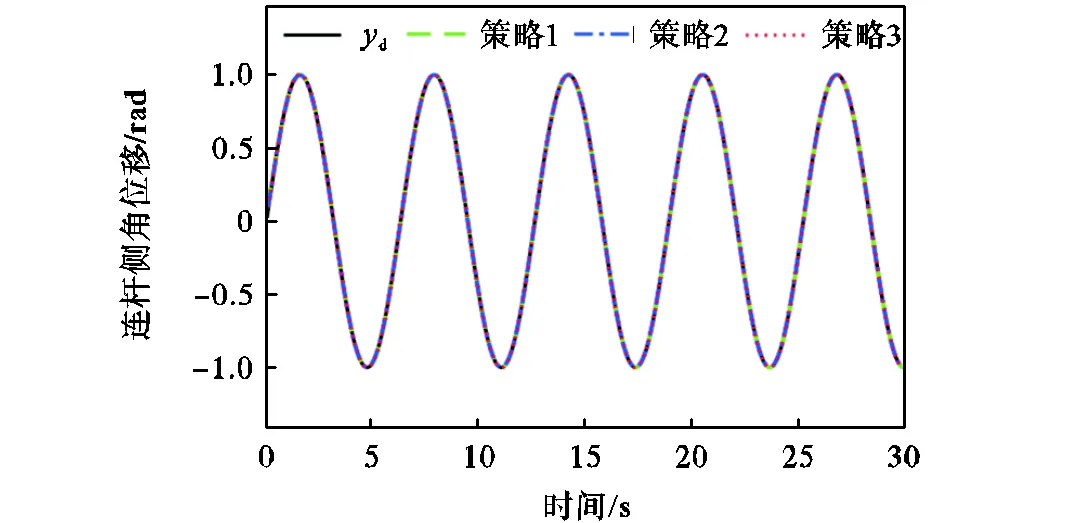
图8 3种控制策略下的连杆侧轨迹跟踪曲线

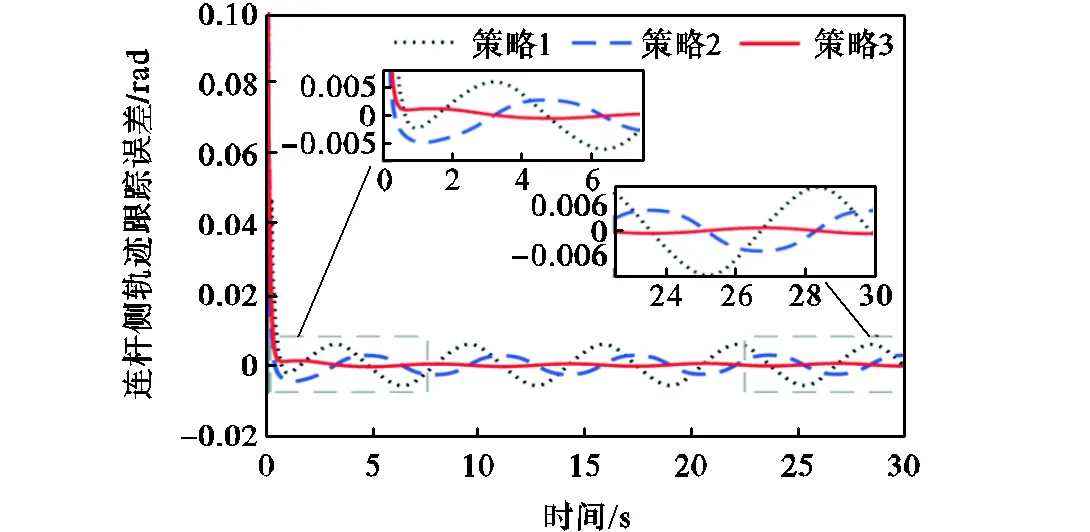
图9 3种控制策略下的连杆侧轨迹跟踪误差

图10 3种控制策略下对连杆侧模型不确定项的逼近

图10和图11分别展示了3种控制策略对连杆侧和电机侧的模型不确定项的逼近效果，可以看到本文所提出的复合动态面控制策略3比策略1和策略2的逼近效果更好．

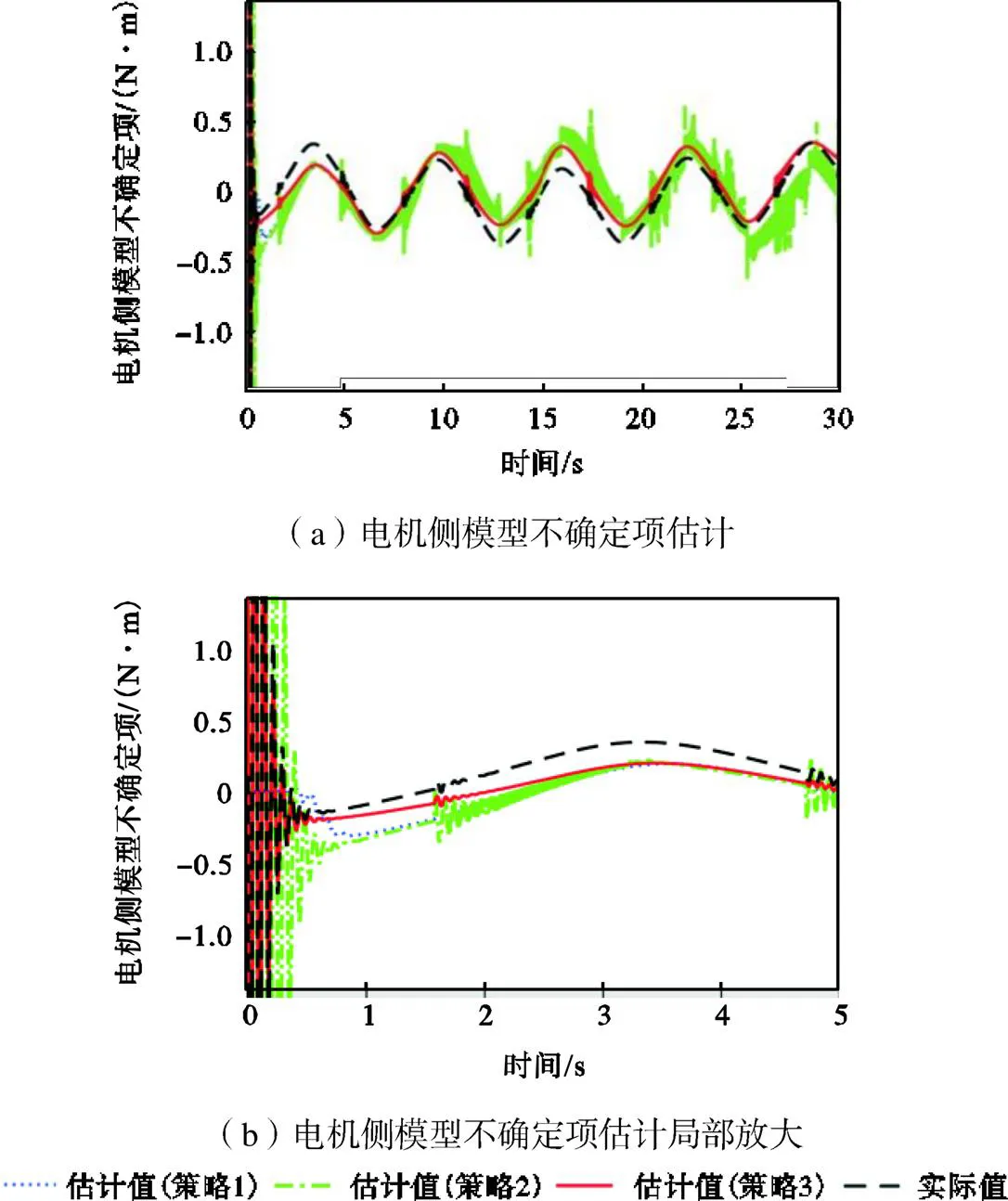
图11 3种控制策略下对电机侧模型不确定项的逼近

为了更清晰地评估控制策略1、策略2、策略3的性能，使用下面的性能指标[2]：误差平方积分(integral of square error，ISE)、误差绝对值积分(integral of the absolute error，IAE)和时间乘以误差绝对值积分(integral of time multiplied by the absolute value of error，ITAE)，具体可表示为

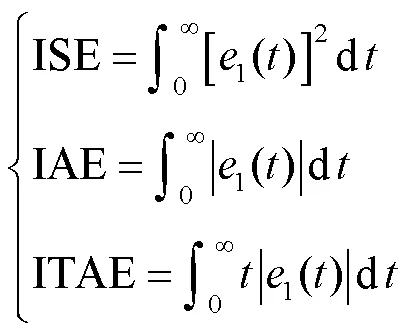
表2给出了3种控制策略的ISE、IAE和ITAE的值．从表2可以明显看出所提出的复合动态面控制策略3的ISE、IAE和ITAE的值低于采用RBF神经网络逼近器的自适应动态面控制策略1、具有规定性能约束的自适应神经网络动态面控制策略2．以上分析证明了所提出的复合动态面控制策略在面对具有参数不确定性、建模误差和未知扰动的单连杆柔性关节系统时，比另外两种控制策略具有更好的瞬态和稳态性能、更高的轨迹跟踪精度和更强的抗扰动能力．

表2 性能指标

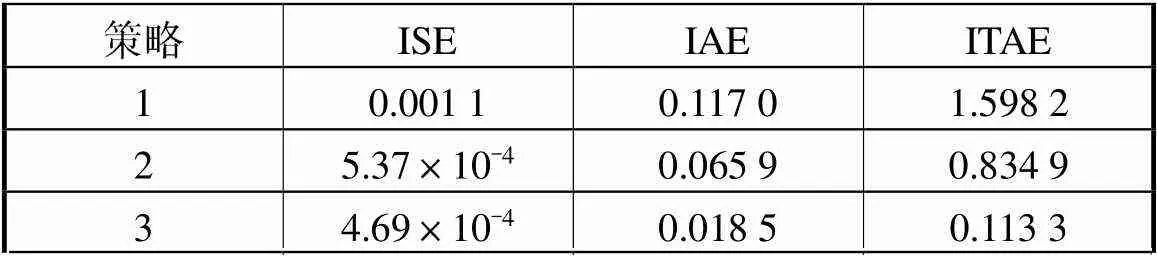
Tab.2 Performance indexes

以上讨论表明，在充分利用自适应鲁棒控制和RBF神经网络的优点的基础上，将预测误差加入自适应参数的更新律中，同时结合约束处理方案可以提高控制器对模型不确定项的逼近精度，进而提高柔性关节系统的跟踪性能和对未知扰动的鲁棒性．

4 结 论

为了进一步提高柔性关节系统的轨迹跟踪性能和扰动抑制能力，本文提出了一种基于动态面控制技术、PPC、参数自适应算法和神经网络的复合动态面控制策略．该策略利用参数自适应算法和神经网络补偿了柔性关节系统的模型不确定项，同时设计约束处理方案保证了误差规定性能约束和提高了系统对未知扰动的鲁棒性．另外，将预测误差加入复合学习自适应律，提高了控制器对模型不确定项的补偿精度．利用李雅普诺夫方法保证了闭环系统中所有信号的半全局一致最终有界性和整个系统的稳定性．对一个单连杆柔性关节系统的仿真结果表明，该系统的跟踪误差能够以规定的性能收敛到原点附近的一个小邻域．同时，与使用RBF神经网络逼近器的自适应动态面控制策略以及具有规定性能约束的自适应神经网络动态面控制策略相比，所提出的控制策略能够取得更优越的跟踪性能和扰动抑制能力．本文得出如下结论．

(1)所提出的控制策略不仅可以保证跟踪误差满足规定性能约束，还具有出色的轨迹跟踪性能和扰动抑制能力．该控制策略无需连杆状态的高阶导数信息，如加速度和加加速度，也无需知道柔性关节系统动力学参数大小．

(2)将预测误差纳入复合学习自适应律中，提供了更好的模型不确定项逼近能力和更高的轨迹跟踪精度．

(3)利用约束处理方案对未知的RBF神经网络逼近误差和扰动的潜在鲁棒性，进一步提高了柔性关节系统的轨迹跟踪精度和抗干扰能力．

［1］ Chaoui H，Sicard P，Gueaieb W. ANN-based adaptive control of robotic manipulators with friction and joint elasticity[J]. IEEE Transactions on Industrial Electron-ics，2009，56(8)：3174-3187.

［2］ 康荣杰，周永翔，杨铖浩. 面向非合作目标的柔性捕获器设计与动力学建模[J]. 天津大学学报(自然科学与工程技术版)，2022，55(2)：174-183.

Kang Rongjie，Zhou Yongxiang，Yang Chenghao. Design and dynamic modeling of a flexible catcher for noncooperative targets[J]. Journal of Tianjin University (Science and Technology)，2022，55(2)：174-183(in Chinese).

［3］ 洪 鹰，徐世超，肖聚亮，等. 基于在线辨识的机器人惯量前馈控制仿真研究[J]. 天津大学学报(自然科学与工程技术版)，2019，52(10)：1069-1080.

Hong Ying，Xu Shichao，Xiao Juliang，et al. Simulation study of robot inertia feedforward control based on online identification[J]. Journal of Tianjin University(Science and Technology)，2019，52(10)：1069-1080(in Chinese).

［4］ Le-Tien L，Albu-Schaffer A. Robust adaptive tracking control based on state feedback controller with integrator terms for elastic joint robots with uncertain parameters[J]. IEEE Transactions on Control Systems Technology，2018，26(6)：2259-2267.

［5］ Wang Z，Hu C X，Zhu Y，et al. Neural network learning adaptive robust control of an industrial linear motor-driven stage with disturbance rejection ability[J]. IEEE Transactions on Industrial Informatics，2017，13(5)：2172-2183.

［6］ Liu J K，Guo Y. Neural network based adaptive dynamic surface control for flexible-joint robots[C]//Proceedings of the 33rd Chinese Control Conference. Nanjing，China，2014：8764-8768.

［7］ Wang M，Ye H P. Adaptive neural dynamic surface control for flexible joint manipulator with prescribed performance[C]//2017 29th Chinese Control and Decision Conference(CCDC). Chongqing，China，2017：5311-5316.

［8］ Selmic R R，Lewis F L. Neural-network approximation of piecewise continuous functions：Application to friction compensation[J]. IEEE Transactions on Neural Networks，2002，13(3)：745-751.

［9］ Yang Y N，Dai T，Hua C C，et al. Composite NNs learning full-state tracking control for robotic manipulator with joints flexibility[J]. Neurocomputing，2020，409：296-305.

［10］ Xu B，Sun F C. Composite intelligent learning control of strict-feedback systems with disturbance[J]. IEEE Transactions on Cybernetics，2018，48(2)：730-741.

［11］ Xu B. Composite learning control of flexible-link manipulator using NN and DOB[J]. IEEE Transactions on Systems，Man，and Cybernetics：Systems，2018，48(11)：1979-1985.

［12］ Tee K P，Ge S S，Tay E H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems[J]. Automatica，2009，45(4)：918-927.

［13］ Bechlioulis C P，Rovithakis G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control，2008，53(9)：2090-2099.

［14］ Guo Q，Zhang Y，Celler B G，et al. Neural adaptive backstepping control of a robotic manipulator with prescribed performance constraint[J]. IEEE Transactions on Neural Networks and Learning Systems，2019，30(12)：3572-3583.

［15］ Zhang J X，Yang G H. Low-computation adaptive fuzzy tracking control of unknown nonlinear systems with unmatched disturbances[J]. IEEE Transactions on Fuzzy Systems，2020，28(2)：321-332.

［16］ Spong M W. Modeling and control of elastic joint robots[J]. Journal of Dynamics Systems，Measurement，and Control，1987，109(1)：310-319.

［17］ Wang H M，Zhang Y，Zhao Z H，et al. Finite-time disturbance observer-based trajectory tracking control for flexible-joint robots[J]. Nonlinear Dynamics，2021，106：459-471.

［18］ Xu B，Shi Z K，Yang C G，et al. Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form[J]. IEEE Transactions on Cybernetics，2014，44(12)：2626-2634.

［19］ Polycarpou M M. Stable adaptive neural control scheme for nonlinear systems[J]. IEEE Transactions on Automatic Control，1996，41(3)，447-451.

Simulation Study of Composite Dynamic Surface Control of Flexible-Joint Systems

Hong Ying，Li Huilu，Xiao Juliang，Liu Haitao

(Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300350，China)

Problems such as parametric uncertainties，modeling error，and unknown disturbance occur frequently in the trajectory tracking control of the flexible-joint manipulator. To ensure the control accuracy of the flexible-joint system，a composite dynamic surface control strategy was proposed based on the equivalent dynamics model. The strategy included dynamic surface control technology，parametric adaptive algorithm，neural network approxima-tor，robust compensator，and constraint-handling scheme. First，the controller was designed using dynamic surface control technology to eliminate the “complexity explosion” issue faced during the backstepping approach. Second，the parametric adaptive algorithm was employed to address the parametric uncertainties in the dynamic model of the flexible-joint system. The neural network approximator was utilized to online approximate and compen-sate for discontinuous friction，modeling error，and unknown disturbances in the model. The robust compensator was responsible for the residual error of the first two parts. Concurrently，a constraint-handling scheme was designed to ensure that the tracking error satisfies the prescribed performance constraints and to further improve the robustness of the controller against neural network approximation error and unknown disturbances. Third，a composite learning adaptive law with prediction error was constructed to improve the compensation accuracy of the controller for model uncertainties. The Lyapunov stability analysis demonstrates that the proposed strategy guarantees that all signals in the closed-loop system are ultimately semi-globally uniformly bounded；moreover，the tracking error eventually con-verges to a small neighborhood around zero with the prescribed performance. Finally，the control strategy was simu-lated and validated in Simulink using a single-link flexible-joint system. The results indicate that the composite dy-namic surface control strategy remarkably improves the tracking performance of the flexible-joint system and reduces its overshoot and settling time. This shows that the composite dynamic surface control strategy is more effective and superior to other strategies.

flexible-joint；dynamic surface control；neural network；adaptive robust control；composite learning

the National Natural Science Foundation of China(No. 52175025，No. 51721003).

10.11784/tdxbz202206013

TP241

A

0493-2137(2023)09-0973-12

2022-06-10；

2022-07-05.

洪 鹰（1962— ），男，博士，副教授，hying1122@126.com.Email：m_bigm@tju.edu.cn

肖聚亮，tjxjl@tju.edu.cn.

国家自然科学基金资助项目(52175025，51721003).

(责任编辑：王晓燕)