基于多维子平行六面体模型的可靠性分析方法及应用 *

2023-06-25钟顺江李振聪曹懿莎上官文斌赵克刚

汽车工程 2023年6期

吕辉，钟顺江，李振聪，曹懿莎，上官文斌，赵克刚

（1. 华南理工大学机械与汽车工程学院，广州 510641； 2. 中汽检测技术有限公司，广州 510530）

前言

在汽车结构系统中，受材料特性退化、制造装配误差、工况变化以及主观经验的影响，系统参数不可避免地存在不确定性。在实际工程中，这种参数不确定性会引起系统响应（如应力、应变、固有特性等）产生波动，并影响着结构系统的安全性和适用性［1］。因此，开展不确定条件下汽车结构系统的可靠性研究具有重要的工程意义。

在工程中，可靠性通常定义为在规定的时间内和给定的条件下，完成既定功能的能力。在传统的生产设计中，通常采用安全系数法来减少参数波动对系统性能的影响。为了确保系统安全可靠，往往需要设定很大的安全系数，导致系统设计过于保守。随着不确定性理论的发展，研究人员提出了概率模型［2］、区间模型［3］、模糊模型［4］等，并基于这些模型发展出了一些成熟的可靠性分析方法。然而，以上模型通常没有考虑参数之间的相关性，导致设计结果过于保守。近年来，为有效考虑不确定参数的相关性，人们提出了多维平行六面体模型（multidimensional parallelepiped model，MPM），它可以将独立和相关的不确定参数置于一个统一的框架之内进行研究［5］。Wang 等［6］基于MPM 提出了一种使用样本的统计特征获得不确定参数的边缘区间和相关系数的方法，并引入径向基函数代理模型进行了结构不确定性分析。Zheng 等［7］基于MPM 描述具有相关性的不确定参数，提出了一种基于非概率可靠性的拓扑优化方法。Ni 等［8］通过正则化将MPM转化成区间模型，基于泰勒展开和链式法则提出了一种不确定性分析方法，即1 阶摄动法（first-order perturbation method，FOPM），并分析了参数相关性对可靠性指标的影响。近几年，作者课题组将MPM 和蒙特卡洛仿真技术相结合，有效求解了汽车动力总成悬置系统特性的不确定性响应［9］。

可以看出，基于MPM 进行工程问题的不确定性和可靠性分析已经取得了较多研究成果。随着工程问题日趋复杂，可能还存在一些关键问题需要进一步解决。例如，现有研究主要将MPM 和FOPM 相结合进行可靠性分析，但FOPM 只有在泰勒展开点附近才具有较高的分析精度，也即其仅适用于处理小不确定度或弱非线性问题。然而，在越来越复杂的汽车结构系统中，一些系统参数往往具有较大的不确定度，并且部分参数之间同时具有一定的相关性［10］。MPM和FOPM相结合的方法在处理这类复杂情形时必然会产生较大误差。因此，很有必要提出一种适用于处理系统参数同时具有大不确定度和相关性的可靠性分析方法，以方便研究人员获得更为精确的可靠性设计结果。

针对上述存在的问题，本文基于MPM 建立一种多维子平行六面体模型，并在此基础上提出一种子平行六面体摄动法，用于处理汽车系统参数同时具有大不确定度和相关性的复杂情形；同时，基于子平行六面体摄动法对系统开展不确定性及可靠性分析研究。分析方法能为汽车系统可靠性设计提供参考和指导。

1 多维平行六面体模型

在汽车结构系统中，多源不确定性问题广泛存在。MPM 可将系统不确定参数的独立性与相关性置于一个统一的框架内进行研究［8］。当给定不确定参数的边缘区间和任意两个不确定参数之间的相关系数时，即可构造一个MPM 来量化系统参数的不确定域。

对于具有n个不确定参数Xi(i= 1，2，…，n)的n维问题，定义Xi的边缘区间为其不确定度为。其中和分别代表的中点和半径。描述参数相关性的n维相关矩阵可定义为

基于MPM所构建的不确定域可通过下式描述：

式中：ΔX=X-XC；T= diag(w1，w2，…，wn)；wi= 1/C=RTρ；e=(1，1，…，1)T。

为便于描述，以具有两个不确定参数Xp和Xq的二维问题为例，可根据样本数据建立一个包络所有二维样本点且面积最小的平行四边形，如图1 所示。图1 中的点A定义为“起点”，以“起点A”为端点的两条平行四边形的边定义为“边界区间”，分别表示为和。

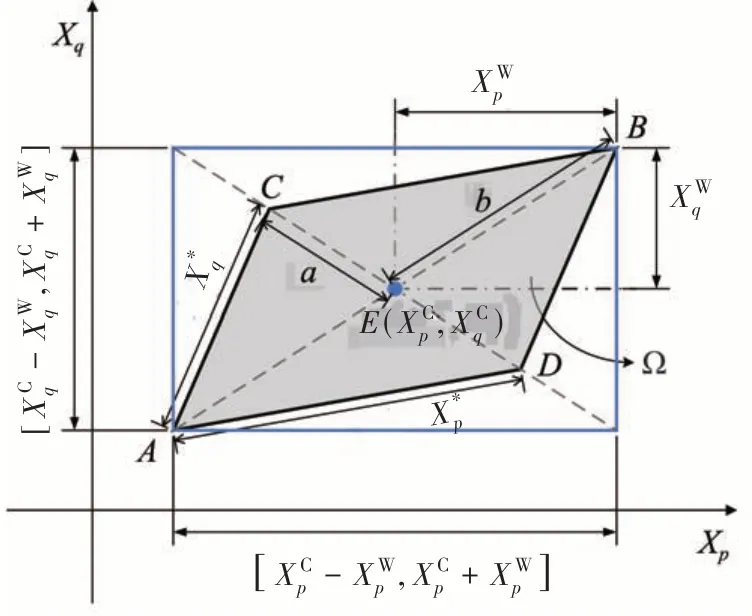
图1 平行四边形模型

在上述平行四边形模型中，变量Xp和Xq之间的相关系数定义为

式中a和b分别表示向量EC和EB的长度。

2 多维子平行六面体模型

本节将提出一种MPM 的拓展模型，即多维子平行六面体模型（multidimensional sub-parallelepiped model， MSPM）。假设n个不确定参数由一n维MPM来描述，为处理其大不确定性，将n维MPM 的每个“边界区间”Xi*均匀划分成m个子区间。通过这种划分方式，总共生成mn个形状相同但位置不同的MSPM。

由式（2）可知，为获得每个MSPM 所描述的不确定域的表达式，需要知道每个MSPM 的形状矩阵Csub和中心点坐标。分析易知。因此，建立MSPM表达式的核心问题为计算每个MSPM 的中心点坐标。为方便分析，下面首先介绍二维的MSPM模型。

2.1 子平行四边形模型

对于具有不确定参数X1和X2的二维问题，假设X1和X2的边缘区间为XI1和XI2；“边界区间”分别为X*1和X*2。X1和X2之间的相关性可通过式（3）表示。

图2 为一个平行四边形不确定域，其中每个“边界区间”被平均划分为m=4 个子区间。计算每个子平行四边形模型中心点坐标的具体步骤如下。

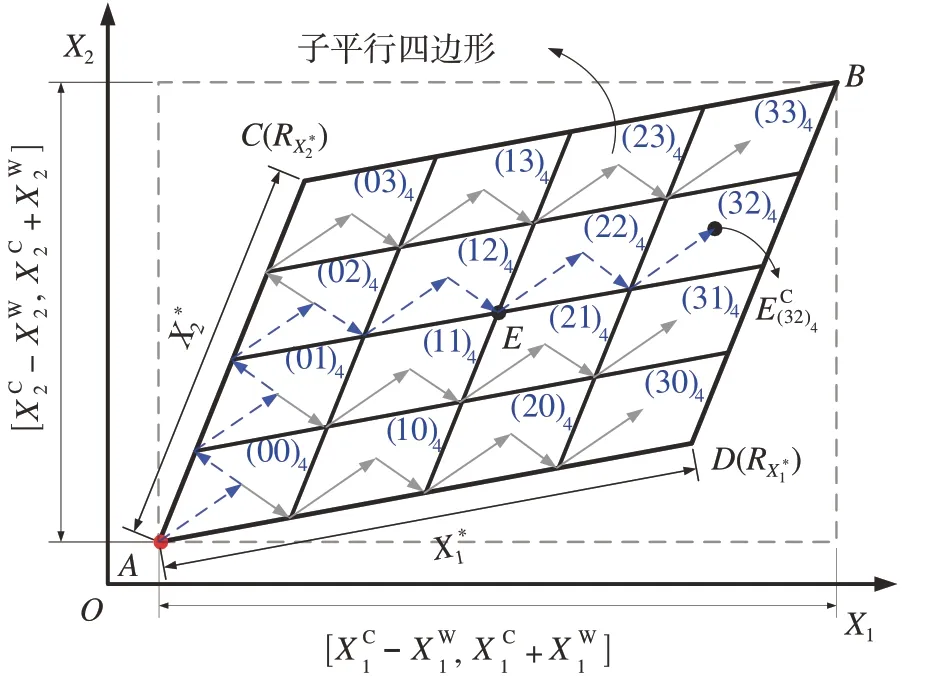
图2 子平行四边形模型

（1）根据图2 所示的规则使用m进制数字(ij)m，i，j= 0，1，…，m- 1 为每个子平行四边形编号。为的第i+ 1个子区间和的第j+ 1个子区间组成的子平行四边形的中心。

（2）将二维情形下的式的不等号改写为等号，可得到“起点A”、“边界区间”X*1的右端点D以及“边界区间”X*2的右端点C的坐标为

并记A点坐标为(AX1，AX2)，计算可得：

基于以上分析，任意子平行四边形模型的不确定域的表达式为

2.2 n维子平行六面体模型

对于更一般的n维问题，变量的边缘区间为XIi，i= 1，2，…，n；“边界区间”为X*=[X*1，X*2，…，X*n]T；相关矩阵ρ表示同式（1）。计算每个n维MPSM 中心点坐标的具体步骤如下。

（1）使用n位m进制数字(ij…k)m为每个n维MPSM 编号。的第i+ 1 个子区间、X*2的第j+ 1 个子区间、…、的第k+ 1 个子区间组成的n维MPSM的中心。为

（2）将式（2）的不等号改写为等号，可得到“起点A”以及所有“边界区间”的右端点的坐标。由此进一步求得MPM 中心点到所有“边界区间”右端点的向量坐标。

（3）根据n维MPSM 的划分规则以及向量加法，可得坐标系原点O到任意n维MPSM 中心点的向量的坐标。

“边界区间”X*i的右端点的坐标可通过求解方程C-1ΔX= -e-i得到。由此，任意“边界区间”X*i的右端点坐标为

式中：ρp是相关矩阵ρ的第p行元素组成的行向量；e-i=[11，…，1i-1，- 1i，1i+1，…，1n]T表示第i个元素为-1，其余元素为1的列向量。

基于上述过程，可得到任意n维MPSM 的中心点坐标为

因此，任意n维MPSM的不确定域表达式为

3 基于MSPM 的非概率不确定性及可靠性分析

为有效地处理汽车结构系统中不确定参数同时具有大不确定度和相关性的问题，本文提出了一种基于MSPM的非概率不确定性及可靠性分析方法。

3.1 非概率不确定性分析

假设系统响应函数为φ(X)，为求得φ(X)的不确定边界，将描述系统参数大不确定性和相关性的MPM 划分为一定数量的MSPM。这样不确定参数的不确定域被划分为多个子不确定域，从而在每个子不确定域中，不确定参数只具有较小的不确定度。为便于描述，将MPSP 的n位m进制数字编号(ij…k)m转化为十进制数字编号r=imn-1+jmn-2+…+km0+ 1，r= 1，2，…，mn。

在第r个MPSM中，系统响应函数φ(X)经正则变化转化为Φ(δ)r。Φ(δ)r可由其在子不确定域中心点δC处的1阶泰勒展开式近似替代：

式中：ΔXq=[0，…，ΔXq，…，0]；ΔXq为一微小增量。考虑到，系统响应函数为

考虑到δi∈[ - 1，1]，i= 1，2，…，n，所以Φ(δ)r的最大值和最小值可以由下式确定：

最后，通过汇总分析所有MSPM 子不确定域中Φ(δ)的极值，可确定原大不确定度问题的系统响应函数φ(X)的上下界分别为

为表述方便，上述非概率不确定性分析方法简记为子平行六面体摄动法（sub-parallelepiped perturbation method，SPPM）。

3.2 可靠性分析

在汽车结构系统中，由失效准则确定的极限状态函数为

式中：Xi(i= 1，2，…，n)为系统不确定参数，类似系统性能响应函数；g(X)为极限状态函数，也存在不确定性，记g(X)的最大和最小值分别为g(X)U和g(X)L。根据非概率可靠性理论，可定义系统的非概率可靠性指标［11］为

当η> 1 时，g(X)的下界大于0，系统可靠；当η< -1 时，g(X)的上界小于0，系统失效；当-1 <η< 1 时，g(X)可能大于0 也有可能小于0，系统可能可靠也可能失效。

极限状态函数g(X)一般为由系统响应函数φ(X)与常数C组成的函数，即g(X) =C±φ(X)。因此，进行系统可靠性分析时，可以直接利用不确定性分析中φ(X)的上下界计算得到g(X)的上下界，由此得到系统的可靠性指标η。

4 算例分析

4.1 汽车声固耦合系统模型

汽车车身结构和内部声场构成一典型的声固耦合系统。在本算例中，引用文献［12］中的一简化声固耦合模型进行分析，如图3所示。声腔为空气域，声腔和顶部的耦合界面为弹性边界，其余为刚性边界。

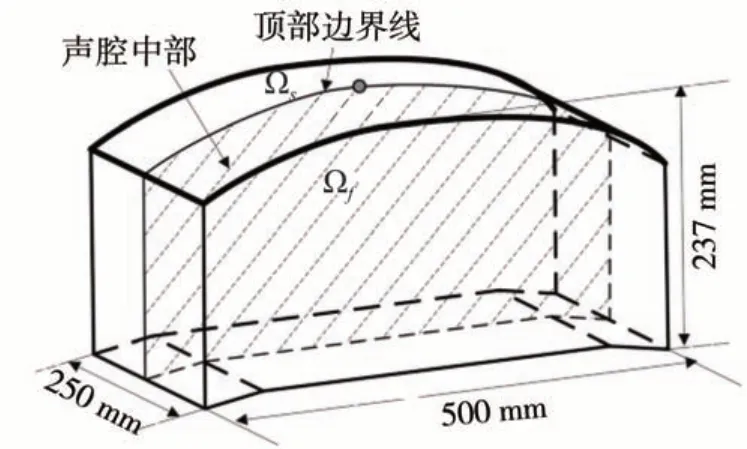
图3 声固耦合系统模型

该系统中声速c与空气的密度ρf具有负相关性［13］，因此，设置其不确定度为30%，相关系数为-0.3。壳结构的弹性模量E、泊松比υ、厚度t和密度ρs则设为确定参数，具体取值如表1所示。模型顶部边界线中点处竖直方向上施加频率为200 Hz 的单位正弦激振力。

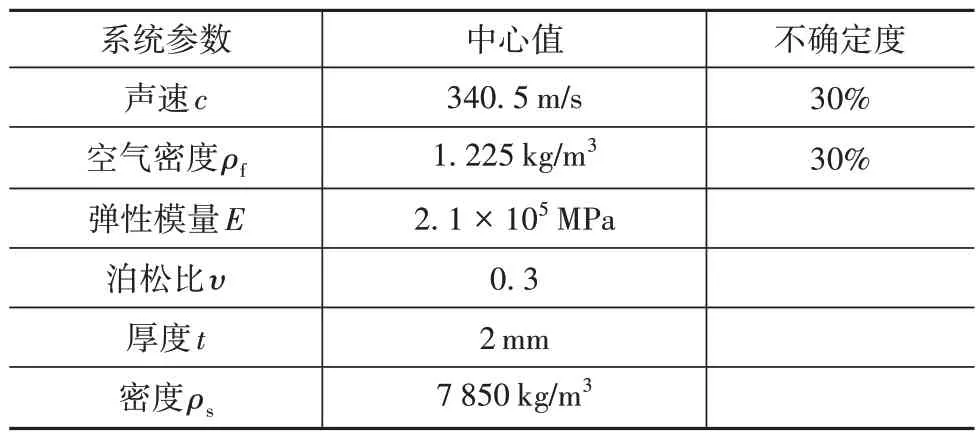
表1 声固耦合系统不确定参数取值

蒙特卡洛仿真（Monte Carlo simulation，MCS）在样本规模足够大的情况下能获得较高的计算精度，通常用于验证不确定性分析方法的有效性，因此本文选取MCS 作为参考方法［14］。使用MCS、FOPM 以及SPPM 计算沿顶部边界线分布的声压响应区间，结果如图4 所示。其中，SPPM（m）符号代表划分m个子区间的SPPM 方法。基于MCS 的概率收敛特性，此处设置其样本数量为10万。

图4 系统声压响应区间

鉴于系统声压响应的数量级较小，图4中FOPM和SPPM 的计算结果与MCS 的计算结果对比不明显。为了清晰地展示FOPM 和SPPM 预测声压响应区间的准确性，图5 给出了以MCS 为参考时，FOPM和SPPM计算的相对误差。

图5 声压响应的计算误差

从图5可知，FOPM 求得的部分节点的声压响应区间存在较大误差。特别地，FOPM 计算得到的节点8（x=215.7 mm）的声压下界相对误差高达36.39%。而对SPPM（2）来说，除节点8 处的声压响应下界误差为10.19%外，其余各节点的声压响应上下界的相对误差均在6%以下。此外，还可知SPPM（4）和SPPM（8）求得的声压响应上下界的相对误差均在1.5%以下，较多节点处的相对误差在0.1%附近。这说明，FOPM求得的系统声压响应区间差强人意，部分节点误差比较大；SPPM（2）计算的声压响应区间则较为准确，而且随着划分多维子平行六面体数量的增多，SPPM能获得更加精确的计算结果。

此外，MCS 计算系统响应特性的时间约为112800 s；FOPM 的计算时间约为6 s；SPPM（2）、SPPM（4）和SPPM（8）的计算时间分别为22、90 和358 s。因此，相较于FOPM，提出的SPPM 在略微降低计算效率的情况下有效提高了计算精度。

对此声固耦合系统进行可靠性分析时，考虑以下极限状态函数：

式中φ(X)为本算例中节点8（x= 215.7 mm）的声压响应。根据式（19），基于不确定性分析的结果，可计算得到节点8声学响应特性的可靠性指标，如表2所示。

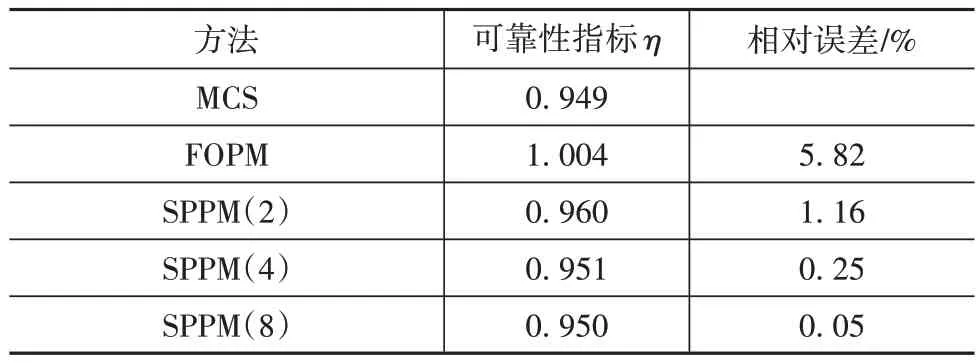
表2 声学响应的可靠性指标

从表2 可知：MCS 求得的非概率可靠性指标为0.949，系统有可能失效也有可能安全；而基于FOPM求得的可靠性指标大于1，说明系统设计是绝对可靠的；基于SPPM 求得的可靠性指标均小于1但大于-1，所以系统有可能失效也有可能可靠。可见，对系统参数同时具有大不确定度和相关性的声固耦合系统进行可靠性分析时，FOPM 带来的误差可能会影响可靠性分析结果，甚至造成系统可靠性评估错误。此外，还可知随着划分的多维子平行六面体数量的增加，基于SPPM计算的可靠性指标误差随之减小。

4.2 汽车盘式制动器系统

在本算例中，将以汽车盘式制动器系统的振动稳定性为研究对象，进一步验证所提出方法的有效性。图6 为一盘式制动器系统模型，在系统制动工作过程中，如果其处于不稳定状态，将会产生制动尖叫噪声［15］。文献［15］中给出该系统7.2 kHz 处的制动尖叫响应函数为

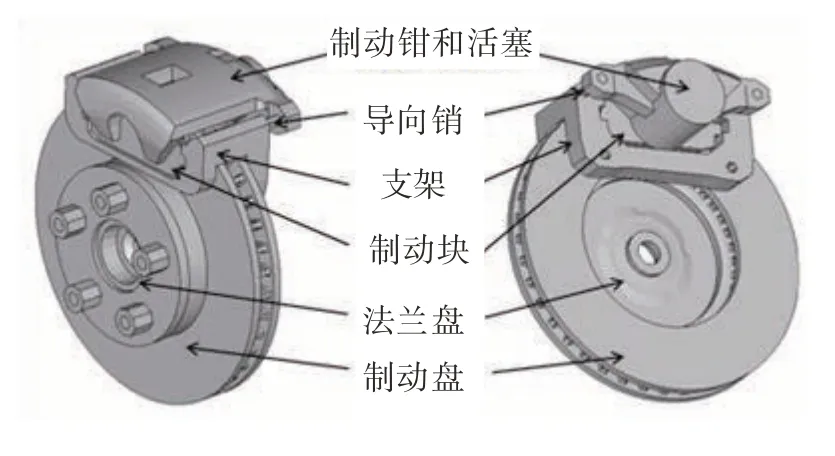
图6 盘式制动器模型

式中：ζ(X)为系统第7阶复模态阻尼比，即制动尖叫响应函数；f为摩擦因数；ρl为摩擦材料密度；p为制动压力；El为摩擦材料弹性模量。这些参数均视为不确定参数，表3给出了其不确定取值情况。

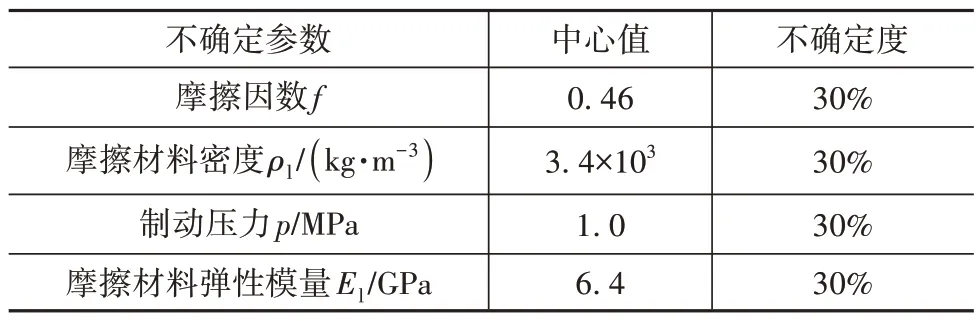
表3 制动器系统不确定参数取值

在制动器系统中，摩擦因数f与制动压力p［16］、摩擦材料的密度ρl与弹性模量El［17］通常具有一定的相关性。本算例设定不确定参数f和p的相关系数为0.3，不确定参数ρl和El的相关系数为0.3。

由MCS、FOPM 和SPPM 分别计算得到的系统尖叫响应区间结果如表4 所示。其中，MCS 的样本数为10万。

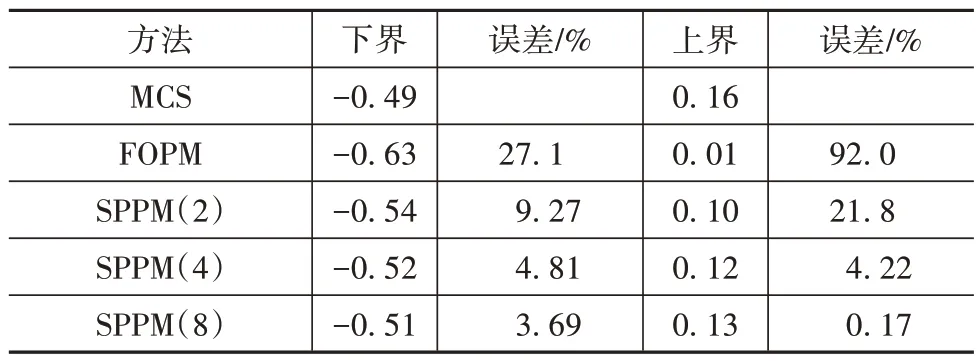
表4 尖叫响应的上下界及计算误差

从表4可知：FOPM 求得的响应下界和上界的相对误差较大，分别达到了27.1%和92.0%；而划分2、4、8 个子区间的SPPM 求得的下界和上界的相对误差分别为9.27% 和21.8%、4.81% 和4.22%、3.69%和0.17%。由此可知，随着SPPM划分的多维子平行六面体数量的增加，其计算的相对误差随之减小。在计算时间方面，MCS的计算时间约为107 s，而FOPM 和SPPM 的计算时间均小于1 s，计算效率远高于MCS。

由控制理论可知：制动器系统的复模态阻尼比若为正，则系统处于稳定状态；反之，系统不稳定。但由于对制动器系统进行仿真分析时，忽略了材料阻尼的影响，所以大部分学者将阻尼比大于-0.01视为稳定模态［18］。因此，考虑以下极限状态函数进行系统可靠性分析：

根据式（21），基于不确定性分析的结果，可计算得到系统稳定的可靠性指标，如表5所示。

表5 制动器系统稳定性的可靠性指标

从表5可知，基于以上3种方法计算的非概率可靠性指标均大于-1 且小于1。因此只考虑式（21）极限状态函数时，系统响应可能可靠，也可能失效。另外，以MCS为参考，基于FOPM 和SPPM（2）计算的非概率可靠性指标η的相对误差较大。而基于SPPM（4）和SPPM（8）计算的可靠性指标则更加接近参考值。这也同时说明划分多维子平行六面体的数量越多，基于SPPM计算的非概率可靠性指标越精确。

4.3 电动车动力总成悬置系统

为再进一步验证所提方法的有效性，考虑一个具有9 个不确定参数的电动汽车动力总成悬置系统（powertrain mounting system，PMS）的不确定性及可靠性分析问题。PMS作为影响汽车舒适性的重要子系统之一，其固有特性分析是汽车振动与噪声性能分析的一项重要任务。图7 为某一电动汽车的PMS模型，布置方式为三点式横向布置，电机总成质量为92 kg。系统其它主要参数如表6～表8所示。

表6 总成的转动惯量和惯性积kg·m2

表7 悬置的静刚度N/mm

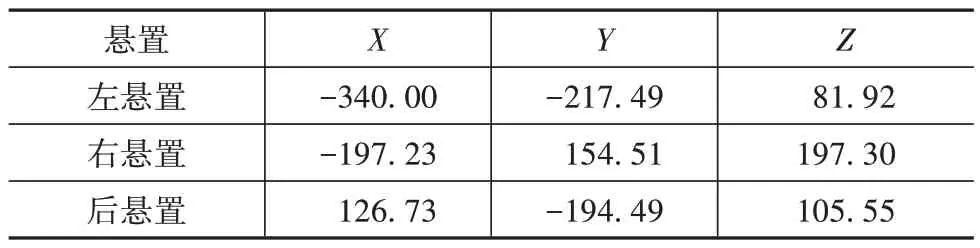
表8 悬置的安装位置mm

图7 电动车PMS模型

电动车PMS 橡胶悬置的刚度参数往往具有一定的不确定性和相关性，且已有研究大多数选择悬置刚度作为PMS 的主要研究参数。此外，对于PMS的振动特性，通常主要关注其竖直方向（Z方向）和绕定转子中心线旋转方向（θY方向）的固有特性响应。因此，本文重点研究PMS 各悬置的三向刚度存在不确定性和相关性时Z和θY方向的固有特性响应。系统固有特性的求解过程详见文献［19］。

本算例中，悬置各刚度参数的不确定度取为30%，中心值如表7 所示。同一悬置的三向刚度参数之间两两存在相关性，设其相关系数均为0.3；而不同悬置的刚度参数则相互独立。

使用MCS、FOPM 和SPPM 分别求得的Z和θY方向的固有特性响应区间及相对误差，结果如表9～表12所示。其中，MCS样本数设为1000万。

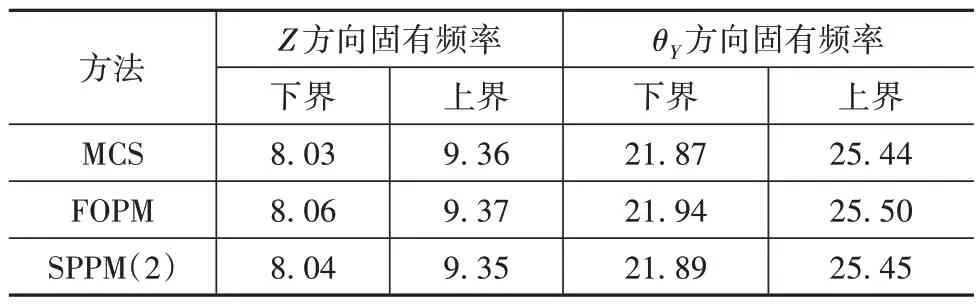
表9 PMS的固有频率Hz

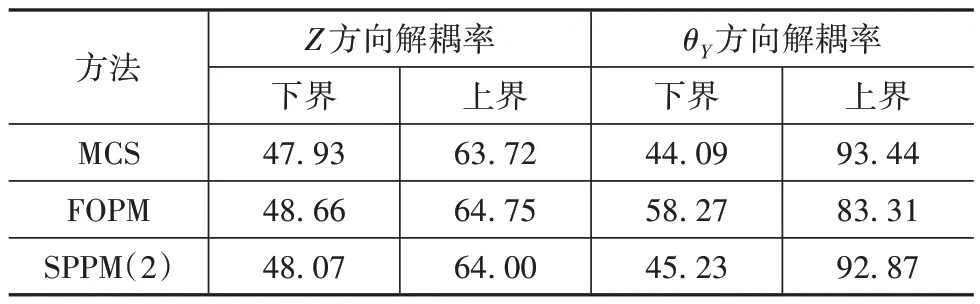
表10 PMS的解耦率%

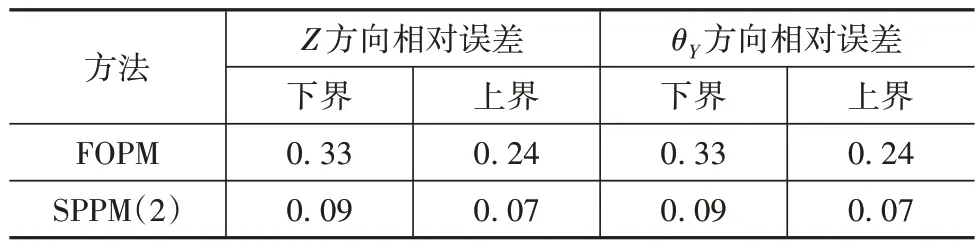
表11 固有频率的计算误差%

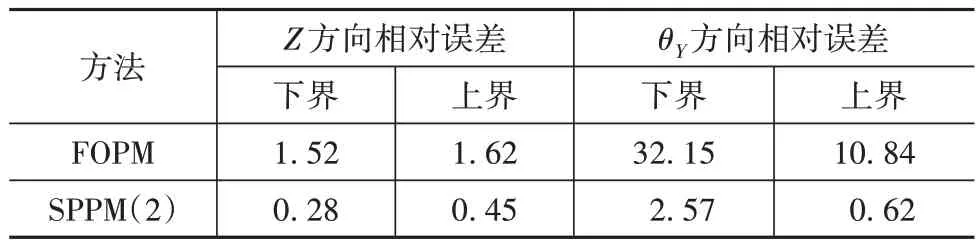
表12 解耦率的计算误差%

从表11可知，对于固有频率响应，FOPM 求得的响应上下界误差均小于0.5%；而SPPM（2）求得的响应上下界误差均小于0.1%。从表12 可知，对于解耦率响应，FOPM 在求解θY方向解耦率上下界时出现较大的误差，分别为10.84%和32.15%；而SPPM（2）求得的响应误差则均小于2.6%。综上所述，由于固有频率响应函数的非线性程度较小，FOPM 和SPPM都有着较高的精度；但对于非线性程度较高的解耦率函数，FOPM 计算结果出现较大偏差，SPPM（2）则能更好地预测其响应区间。在计算时间方面，MCS 的计算时间为1235.43 s，FOPM 耗时0.13 s，SPPM（2）耗时5.69 s，可见FOPM 和SPPM（2）计算效率远高于MCS。

在PMS 设计中，通常要求解耦率应尽可能大，以获得良好的隔振性能。一般考虑解耦率大于80%，进而可得以下极限状态函数：

式中：dZ(X)为Z方向的解耦率；dθY(X)为θY方向的解耦率。表13 给出了PMS 解耦率设计的可靠性指标。

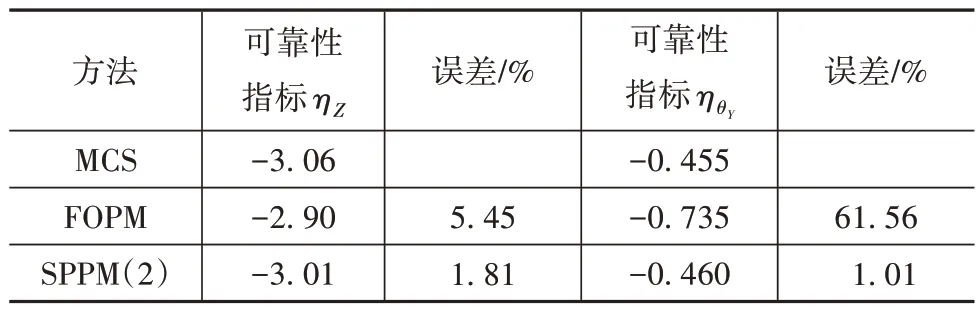
表13 解耦率的可靠性指标

从表13 可知，以MCS 作为参考，对于可靠性指标ηZ而言，基于FOPM 计算的相对误差为5.45%，而基于SPPM（2）计算的相对误差仅为1.81%；对于可靠性指标ηθY，基于FOPM计算的相对误差为61.56%，而基于SPPM（2）计算的相对误差为1.01%。可以看出，基于SPPM（2）计算的可靠性指标精度远优于FOPM。