矢量-角度几何映射的方向重要抽样分布函数近似化方法及多失效模式可靠性分析 *
2023-06-25王俊峰陈吉清兰凤崇刘青山
王俊峰,陈吉清,兰凤崇,刘青山
(1. 华南理工大学机械与汽车工程学院,广州 510640;2. 华南理工大学,广东省汽车工程重点实验室,广州 510640)
前言
在实际工程中,结构设计的不确定性和随机性普遍存在,如制造和安装误差、材料模型和属性、随机载荷以及其他不确定因素。可靠性分析已成为一种趋势和必要,也是可靠性设计优化的基础环节。目前已开发了多种可靠性分析方法,1阶和2阶可靠性方法是分别在极限状态面设计点处进行Taylor 展开取至一次和二次项来近似估计故障概率,这对处理强非线性问题存在缺陷[1]。而蒙特卡洛(Monte Carlo, MC) 模拟作为一种替代方法,用来估计基于样本点的计算模拟的故障概率,在非线性和维度上具有鲁棒性,其缺点是在小概率问题上,需要大量样本进行函数评估,比较耗时。为提高模拟效率,提出了各种改进方法,如重要抽样(importance sampling,IS)、子集模拟[2]、线抽样[3]、方向抽样 (directional sampling, DS)[4]和方向重要抽样 (directional importance sampling, DIS)[5-6]等方法,在不同程度上减少了计算负担。
本文中对DIS 方法进行研究,因为该方法在处理非线性问题方面具有优势,其基本理论来源于DS方法[7]。Ditlevsen 等[8]结合IS 方法思想提出了DIS方法,进一步提高了计算效率。目前DS 和DIS 方法已被应用于结构可靠性分析中,如时不变可靠性分析[8]、灵敏度分析[6,9-10]和可靠性优化[11]。该方法也可与机器学习或元模型结合应用,如神经网络[12]和Kriging方法[13]。
在DIS 方法中,有一个重要的环节是基于设计点来生成重要方向矢量 (important direction vectors,IDVs)。由于向量的多维性,原始概率密度函数(probability density function, PDF) 很难直接通过编程生成IDV,因此重构PDF 是必不可少的步骤。Gong等[14]结合DIS和径向基函数神经网络来计算隐式极限状态函数 (limit state function, LSF) 的设计点,并构建了重要性抽样的联合PDF,确保更多的样本属于失效域。Shayanfar 等[1]通过Kullbak-Leibler交叉熵度开发了一个接近最优的采样函数,并通过一个封闭的更新规则使其具有自适应性。
通常使用Ditlevsen 等[8]提出的重建方法。该方法通过创建一个通过原点并与设计点位置矢量正交的辅助超平面,采用了降维的思路。IDV 可以被分解为设计点方向的向量(一维空间)和超平面上的向量(n-1 维空间)。超平面上的向量可以通过将随机向量投射到超平面上得到,而设计点方向的向量则通过缩放这个方向的单位向量得到,这很容易通过程序实现,该方法也被Guo 等[15]应用。在作者之前的研究中,提出了另一种降维方法[16],基于矢量-角度几何映射的DIS 可靠性分析方法,先构造重要方向角度(important direction angle, IDA) 的PDF,然后将IDA 映射到多维IDV 上。IDA 的PDF 可以分析IDA/IDV 在高斯空间的分布特征,样本量分配方面更灵活。但该方法得到的分布函数是基于理论推导,涉及到积分等复杂计算,在IDVs 生成方面没有给出高效的实施策略。
基于此,为高效生成IDVs,对复杂分布函数进行近似构造,利用一维拉丁超立方方法插值抽样,快速得到具有分层均匀性的样本。另外,从多设计点、多失效模式、非线性和维度等方面讨论了DIS 方法的适用性和特点,并通过数值算例和车身工程问题进行了验证,为方法的改进以及可靠性评估提供参考。
1 方向重要抽样与样本生成
1.1 失效概率及其无偏估计
DS/DIS方法适用于变量服从独立的标准正态分布的可靠性分析,设随机向量x=(x1,x2,…,xn)T用极坐标表示为x=RA,其中R为极半径,A为向量x对应的单位方向向量。在极坐标下,DS 方法的失效概率PF可表示为[17]
式中:X、R和A分别是x、r和a的集合;φRA(r,a)为R和A的联合PDF ;(·)为自由度为n的卡方分布的累积分布函数 (cumulative distribution function,CDF);EA( ·)表示PDF 为fA(·)的期望值;fA(·)为单位方向向量A的PDF,由于DS 方法为均匀分布,因此,fA(·)服从单位球面上的均匀分布,可由每个分量随机生成。
生成N个样本ai(i=1, 2, ... ,N),如图1所示,以二维空间为例,每个ai对应一个子失效域Fi(i=1,2, ... ,N),并指向子失效域面的中心点di(i=1,2, ... ,N)。这些中心点也位于实际的极限状态失效面g(x)=0 上。容易看出,极限状态下的失效面是由一系列子失效域面近似组成。因此,失效概率可近似描述为
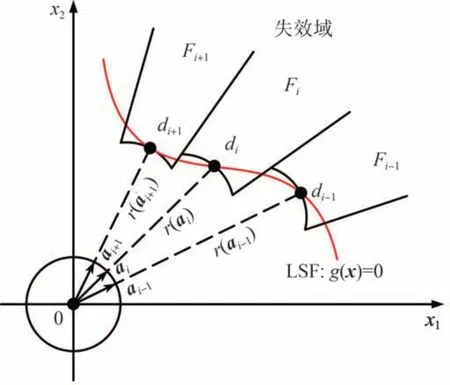
图1 DS方法样本与失效域示意图
为提高模拟效率,利用IS 方法的思想,可让更多的样本矢量指向对失效概率有较大贡献的区域,即与设计点矢量夹角在90°范围内的重要区域。如图2 所示,以二维高斯空间为例,过原点的虚线与设计点矢量aX互相垂直,虚线作为分界线,其矢量aX所在的一侧区域作为重要区域,该区域重要方向矢量 (IDVs) (如a1和a2) 与aX构成重要方向角(IDAs) (如θ1和θ2,均小于90°)。基于此,Ditlevsen等[8]提出了DIS方法,通过构建一个重要性PDF来代替原来的均匀PDF (即fA(·)),实现更多的IDVs 被引导到重要区域,从而提高抽样效率并加快了仿真过程的收敛速度。
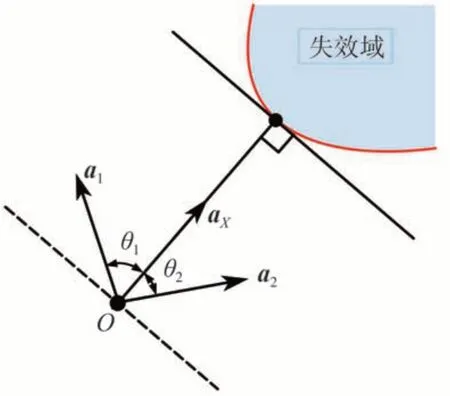
图2 重要区域、重要矢量和重要角
假设IDV 的PDF 为hA(a),DIS 方法失效概率由式 (1) 改写为[18]
由DIS 方法产生N个样本,失效概率的无偏估计为[17]
式中1.96表示置信水平为95%对应的系数。
1.2 分布函数与样本生成流程
DIS方法的重要PDFhA(a) 可描述为
式中:Φ(·)表示标准高斯分布的CDF;β为可靠性指标;>0 表示a与设计点矢量aX夹角小于90°,即a属于重要方向矢量;≤0 表示矢量a没有指向重要区域,因此,对应概率为0。
为更好地适应各种失效面,对DS 和DIS 的PDF进行加权求和,加权hA(a)可表示为
从式(7)可以看出,DIS 的PDF 是关于矢量建立的,文献[17]应用接受/拒绝采样方式生成IDVs,需要大量的样本作为代价,效率较低,比较通用的是Ditlevsen 等[8]提出的抽样方法,首先是随机抽样,即均匀方向抽样,然后对n维随机向量X进行分解,如图3所示。位于过原点并与ZL平行的n-1维超平面Z⊥上。加入一个随机变量V,假设V的CDF为
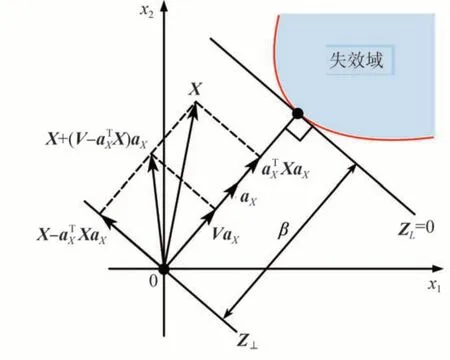
图3 DIS方法抽样示意图
矢量X+(V-aTXX)αX便服从式 (7) 的概率分布。向量的分布函数转换为一个一维变量V的分布函数,容易实现抽样。采用逆CDF 方法对V进行抽样,即v=F-1V(u),u是服从均匀分布U(0,1) 的随机数。逆CDF表示如下:
通过这种方式,可获得服从式 (7) 分布的IDVs。用到的参数有可靠性指标β、变量维度n以及权重系数p。文献[18]中对该方法的编程实现提供了开源代码。
2 矢量-角度几何映射的DIS 抽样函数近似构造
2.1 矢量-角度几何映射的DIS抽样方法
上节介绍一种生成IDVs 的抽样函数,从图3 可以看出,IDAs 是由X和V共同决定,由于X为随机矢量样本,因此难以控制IDAs,即少量样本情况下可能导致分布特征不准确。而矢量-角度几何映射的DIS 抽样函数可有效避免这个问题,接下来介绍该方法原理以及编程实现。
矢量-角度几何映射的DIS 抽样函数同样是把向量的重要性PDF转化为一个一维的PDF。虽然向量每个维度的分量不易控制,但每个向量与设计点的角度是一维的,如果确定了角度,便可通过几何映射生成相应矢量。因此需要把矢量的重要性PDF转换为角度的PDF,通过生成IDAs 再映射到对应的IDVs。这是该方法的基本原理[16]。如图4所示,θ为IDA,单位向量aV便是θ对应的IDV。单位向量aV可由下式计算得到:
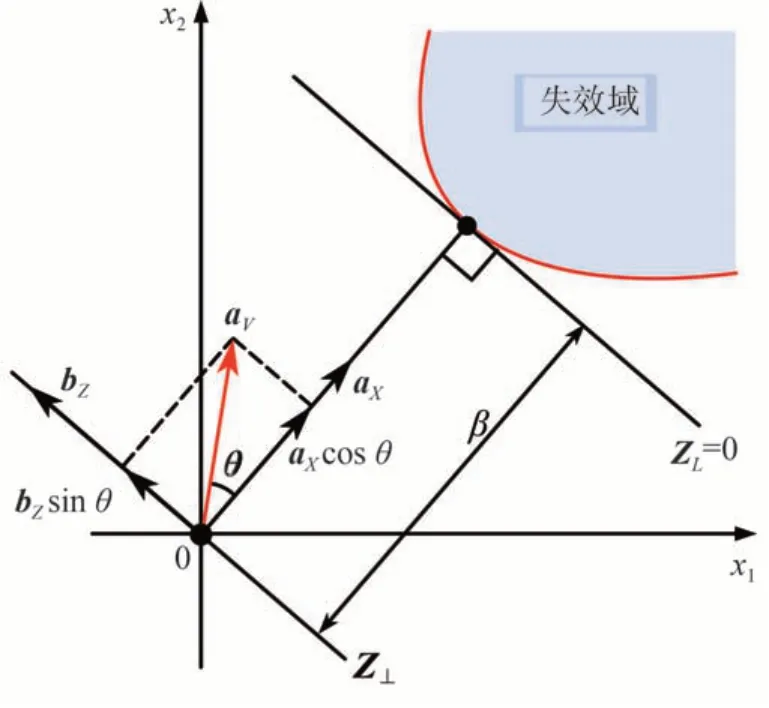
图4 基于矢量-角度映射的DIS方法抽样示意图
式中:aX为单位化的设计点向量;bZ是由上节超平面Z⊥上随机向量X-aTXXaX单位化后的结果。得到的aV同样为单位向量,且与aX的夹角为θ。
而θ的重要性PDF 可在超球坐标系下,利用矢量与角度的概率关系进行推导,推导过程可参考之前的研究工作[16],θ为IDA,因此θ∈[0°,90°),则
式中:gθ(θ|β,n)是关于θ的PDF,与上节方法类似,同样涉及到参数可靠性指标β和变量维度n,此处并没有对PDF 进行归一化处理;Q(β,n)是关于β和n的函数,即β和n确定后,Q(β,n)也唯一确定。β和n对样本分布的影响在文献[16]中有具体讨论。
得到的PDF 对应式 (6) 的PDF,因此,不涉及到参数p。而关于DS 与DIS 方法的加权组合,计算方式与上节不同,而是以p为权重进行样本量分配。假设样本量为N,则用于DS 方法抽样的样本量为N×p,用于DIS 方法抽样的样本量为N×(1 -p),如果不是整数,进行圆整,获得样本后再根据式 (7) 分别做可靠性分析,得到PDS和PDIS。最后计算总体失效概率为
2.2 抽样函数近似构造及插值编程实现
上节提出利用IDAθ来映射生成IDV 的方法,但θ的PDF 较复杂,同时还涉及到β和n两个参数,难以给出类似式 (9) 的逆CDF 显式表达。面对不同的可靠性问题,即β和n变化时,PDF 表达式也会发生改变。文献[16]中也没有提出高效的解决方案。一个解决思路是可利用近似代理模型来解决,比如利用响应面或机器学习构造分布函数的代理模型,然而若对β和n两个参数所有可能值同时考虑到近似模型中,需要大量的样本去学习和验证,比较繁琐和耗时。
本文中提出一种高效解决方法,利用插值函数近似构造,无须对β和n两个参数的所有值都进行学习,而是根据β和n的值实时更新模型,具体步骤如下。
首先,把IDA 均匀分为m个连续的小区间,每个区间间距看做一个步长,近似认为每个步长对应的PDF 是相同的,计算每个步长中点对应的PDF 值pi(i=1, 2, … ,m)。则第j(j=1, 2, … ,m) 个节点标准化后的累计值Pj为
式 (13) 便是近似的CDF 对应值,完成近似构造。近似精度受步长大小的影响,如图5 所示,展示不同步长下近似的标准高斯分布曲线。可以看出,步长区间越小越精确。
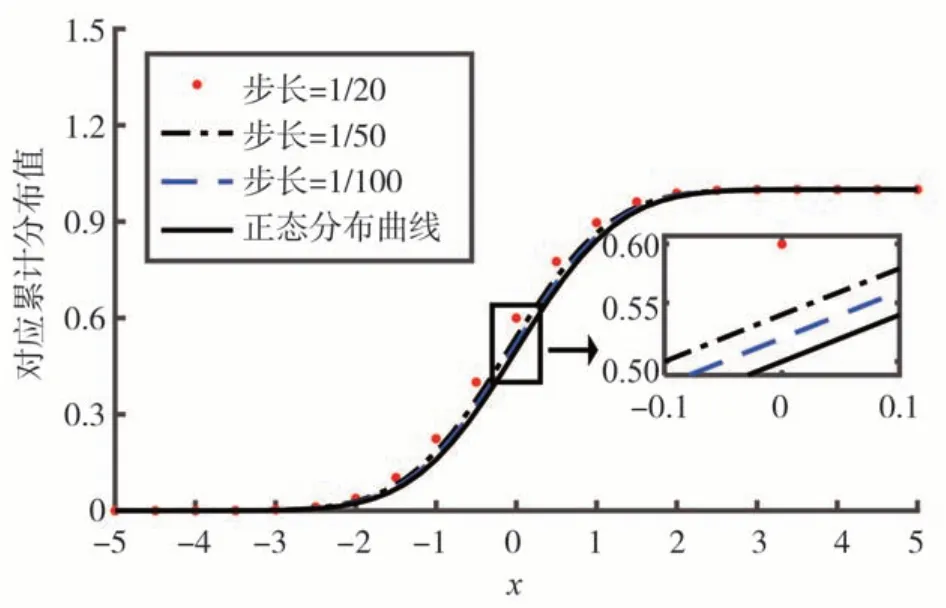
图5 不同步长近似正态分布曲线
其次,实现均匀分层抽样,设样本量为N,对分布值区间[0, 1]均匀等分,可以用一维拉丁超立方函数实现。得到N个样本对应的概率值Ps(s=1,2, … ,N),进一步利用一维线性插值方法计算对应的角度。为保证精度,区间数量m要尽量大,且大于样本量N。
编程实现时,经常会出现插值点不唯一,导致执行程序出错,为此,提出了两种改善策略:一是提高编程环境的数字精度,并对式 (13) 每个节点累加浮点相对精度;另一种方式是找到样本概率值最近的节点作为插值点。两种方式用“try”函数组合起来,如果一维插值方式没有任何语句生成错误则不执行第二种方式,否则执行第二种方式。插值方法还可以通过Kriging 元模型进行构造,这里不做进一步阐述。
编程时式 (11) 可不引入Q(β,n)函数,因为β和n确定时,Q(β,n)也唯一确定,不影响式 (13) 归一化结果,这也是式 (11) 没有采用文献[16]中提出的归一化公式的原因,减少了积分等复杂计算,提高了运算效率。
以设计点D(0, 1) 的二维空间为例,比较上节原方法与本文提出方法产生样本的分布情况。图6给出10 和20 个单位矢量样本在某个随机种子下的分布。从计算用时可以看出,所提方法在计算效率上并没有降低,且产生的样本分布具有分层均匀性,避免样本聚集。而原方法在设计点贡献大的地方缺失样本,还可能存在部分样本聚集的现象,导致分布不均匀。在样本多的情况下,两种方法趋于一致。
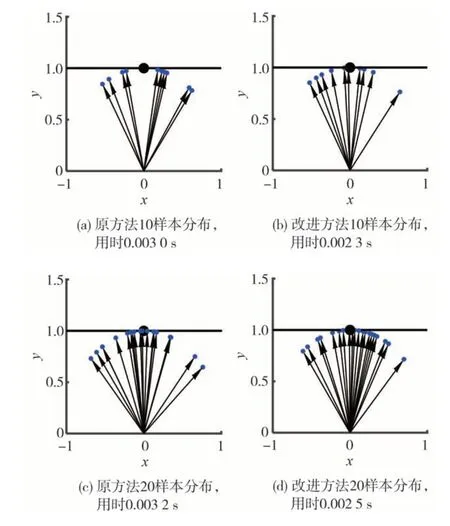
图6 两种方法抽样对比
3 多设计点与多失效模式评估策略
在实际工程中,可能存在多个设计点或失效域,如果考虑一个失效域,其他重要域就会被忽略,就会得到一个被低估的结果。因此,针对不同失效形式,评估策略是分别计算每个失效域的失效概率,然后加权求和,类似式 (12)。设共k个设计点,对应的可靠度为βi(i= 1,2,...,k),第i个设计点失效域的权重为[17]
根据2.1 节所述,分配到DIS 方法的样本量为N×(1 -p),这些样本再分配到第i个设计点失效域的样本量为N×(1 -p) ×wi,同样需要圆整。则式(12) 中PDIS的具体形式为
在一些多性能约束的优化设计或可靠性分析中,涉及到不同失效模式,包括串联失效系统和并联失效系统:串联系统的失效域是所有失效域的并集,即违反任何一个约束都是失效的;而并联系统的失效域是所有失效域的交集,即所有约束都违反时才失效。因此,在多性能函数约束的可靠性分析中,考虑不同失效模式具有重要意义。r(a)求解时应满足[17]:
式中L表示失效LSF的数量,也可以用LSF的形式描述,设gi为第i个LSF的表达式,有
4 算例
本数值算例[19]变量为二维,能以图解的形式更直观地展示该方法在处理串联失效模式和并联失效模式的特征和效果,同时利用数值积分方法计算了失效概率的解析解,来验证该方法的准确性。该算例包含两个LSF:
串联与并联失效域及其设计点如图7 所示。阴影区域为串联系统失效域,阴影区域交集部分为并联系统失效域,并联系统设计点为g1=g2= 0 的交点q*,其坐标为 (1.6184, 2.7806)。串联系统的设计点包括3 个,其设计点可靠度分别为β1、β2和β3。串、并联失效概率的解析解分别为
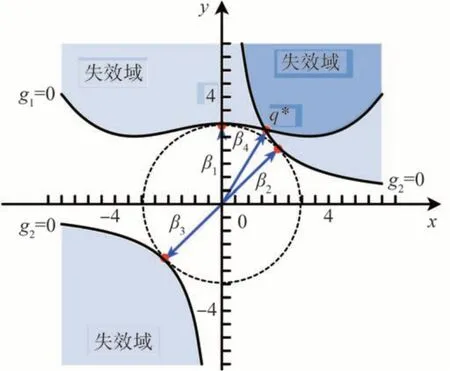
图7 数值算例串并联失效域及设计点
式 (19) 与式 (20) 作为串联系统与并联系统的失效概率基准值,对两种失效模式分别以样本量为20、40、100、150 和200 进行DIS 模拟。失效域均在设计点所在的重要区域,因此参数p设为0,即不需要进行DS 方法模拟。图8 展示了样本量为20 时的模拟示意图。

图8 模拟串并联失效示意图
每组样本仿真30 次,串并联结果分别如图9 和图10 所示。两种失效模式的模拟结果分布类似,不同样本下箱图分布几乎都在10%的误差以内,且平均值接近基准值,模拟结果精度高。随着样本的增加,误差减小,并收敛到基准值,具有较强的鲁棒性和准确性。

图9 串联失效模拟结果分布

图10 并联失效模拟结果分布
5 车身弯扭刚度可靠性分析
白车身的弯曲和扭转刚度对车辆性能有重要影响,比如噪声、振动与声振粗糙度(noise、vibration、harshness, NVH)、安全性、操控性能以及稳定性,还影响车身轻量化程度,是开发过程的一个关键参数,代表车辆的核心竞争力[20]。本案例将所提方法应用于某白车身弯扭刚度的可靠性评估中[21],以解决一个实际工程问题。
取其中8 个钣金件的厚度作为设计变量,结构示意图如图11 所示,变量均服从正态分布,标准差为0.05,均值与设计变量取值范围见表1。
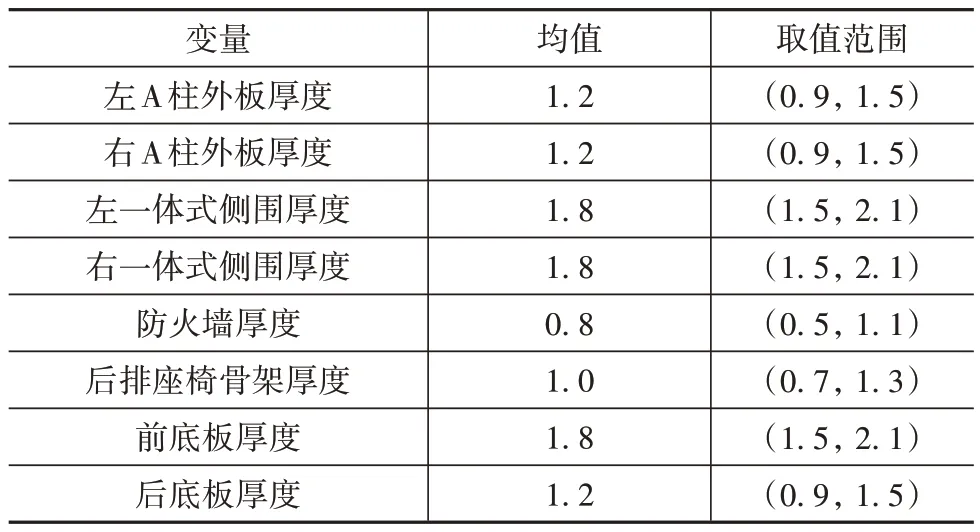
表1 变量名称及其取值mm
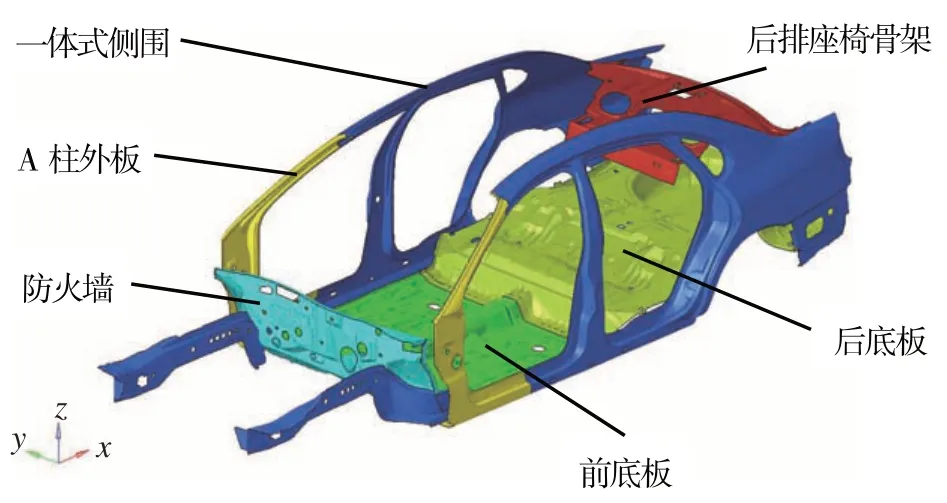
图11 白车身部分结构件
模型竖直(重力)方向为Z方向,施加在门槛梁上的力Fb与施加在减振塔上的力Ft均是Z向力,弯曲工况下左侧和右侧门槛梁下方节点在Z向变形最大值分别设为dLmax和dRmax,设d为减振塔载荷作用点的距离,扭转工况下减振塔左右加载点的Z向位移分别是dL和dR,可以得到弯曲刚度Kb和扭转刚度Kt的计算公式:
定义弯曲刚度和扭转刚度的下限分别是Kbmin和Ktmin,若研究同时失效的概率,属于并联系统,则LSF表示为
复杂工程问题的输入和输出响应为黑箱问题,没有显式表达,因此需要进行试验设计 (design of experiment, DOE),算法采用拉丁超立方采样,对8个变量创建DOE 模型,DOE 分析后利用二次响应面法拟合出式 (21) 的近似代理模型,Kb与Kt拟合的确定系数R-square分别为0.999和0.998,接近1,表明拟合精度高。
进一步建立式 (22) 的LSF 进行可靠性分析。由于变量较多,通过数值积分计算失效概率不再适用,则以样本量为106的MC 方法模拟10 次的平均值作为基准。
以5组不同样本量为例,分别模拟30次,并根据式 (5) 计算95%置信误差限。结果误差分布如图12 所示。误差条显示第25%、50%和75%分位数的误差值,从5 组结果看,75%分位数误差分布均在95%置信误差限内,误差估计从样本量为80起,75%的结果相对误差均在10%以内。
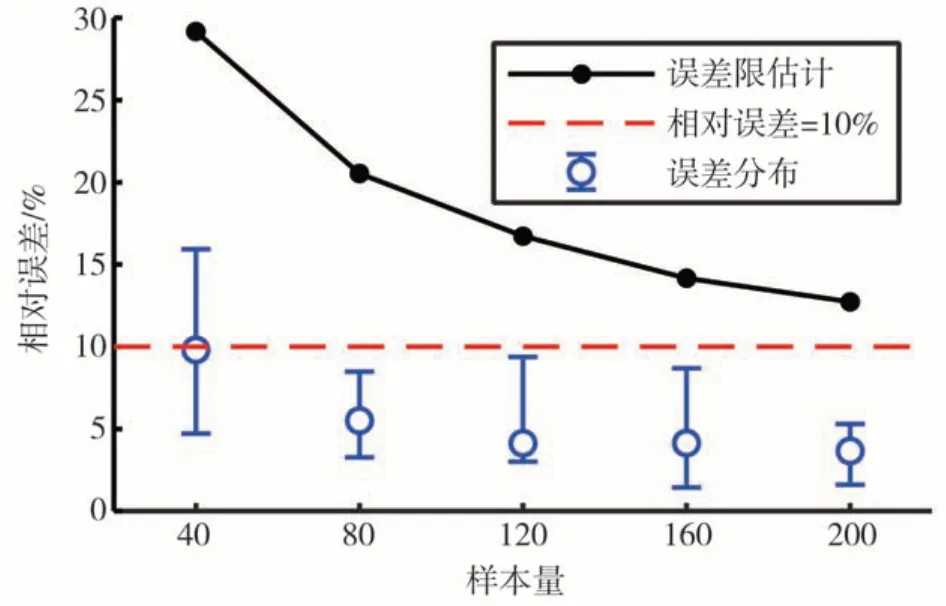
图12 DIS模拟结果误差分布
5 组模拟结果的平均值与MC 方法的基准值比较如表2 所示。平均值相对误差随样本增加而减小,但最大误差也只有2%左右,精度够高,且从图12 可以看出,随着样本增加,误差限变化不再显著。因此,综合权衡计算成本和精度,可采用小样本量多次模拟求平均值的方式获得高精度的结果。
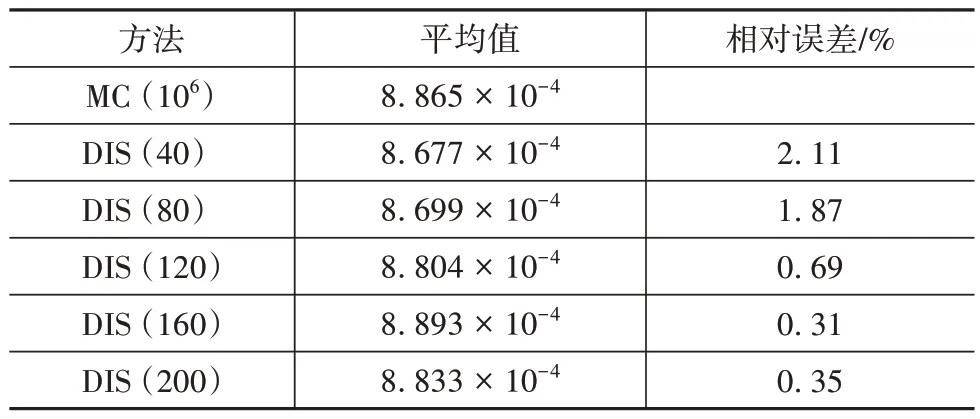
表2 5组DIS模拟结果的平均值及误差
6 结论
提出一种方向重要抽样方法分布函数的近似插值构造方法,先确定一维变量角度的分布函数,利用拉丁超立方采样,获取的重要角度分布具有分层均匀性。由重要角度再映射到矢量样本,有效避免了聚集现象。
利用权重分配方法进行样本分配,灵活处理非线性、多失效模式和多设计点的问题,通过数值算例和车身弯扭刚度的可靠性问题验证了该方法的适用性和准确性。在少量样本的情况下,也可以得到稳定的结果,样本量的选择可以参考置信度误差限,有助于权衡并控制精度与计算成本。采用多次模拟求平均值可以得到更加趋于准确的结果。
