基于MHD角速度传感器的面阵相机模糊图像复原

赵 苓，费 融，李醒飞，拓卫晓，邢伟达

基于MHD角速度传感器的面阵相机模糊图像复原

赵 苓1, 2，费 融1，李醒飞1, 2，拓卫晓1, 2，邢伟达1

(1. 天津大学精密测试技术及仪器国家重点实验室，天津 300072；2. 深海技术科学太湖实验室，无锡 214123)

在轨卫星平台上普遍存在着宽频带、低幅值的微角振动，随着对航天相机探测能力和遥感图像空间分辨率要求的不断提高，微角振动对星载光学系统成像质量的影响更加突出．针对高频微角振动造成的图像模糊问题，提出使用磁流体动力学(magnetohydrodynamics，MHD)角速度传感器测量面阵相机受到的微角振动，并根据面阵相机角运动信息构建点扩散函数，进一步采用基于全变差正则化的图像复原算法实现图像复原，从而提高图像质量．首先，在分析航天相机受到微角振动干扰产生像移原因的基础上，建立像移模型，并根据像点在焦平面上的移动轨迹构建点扩散函数．其次，搭建实验系统模拟航天相机在微角振动环境下的成像过程，在垂直于光轴的方向上施加单频正弦角振动干扰，并使用MHD角速度传感器进行探测．最后，利用基于全变差正则化的图像复原优化算法对模糊图像进行复原，并基于图像的调制传递函数对复原图像质量进行评价．实验结果表明：当微角振动频率在20～ 300Hz内，且产生的像移在13个像元以下时，复原图像的调制传递函数积分面积可达到静态图像积分面积的90%以上，图像细节清晰，对比度得到明显提升．对同一频点进行多次重复实验，结果表明该方法具有良好的重复性．相关实验结果表明，基于MHD角速度传感器的微角振动测量方法和图像复原算法相结合能够显著提高航天相机的成像质量．

MHD角速度传感器；微角振动；成像质量；图像复原

卫星上动量轮等机械部件的运作、姿态的调整等都会产生角振动．相关实验数据表明，卫星平台上普遍存在频率从0.1～1000Hz、幅值从亚微弧度到几百微弧度的微角振动，且幅值会随频率升高逐渐减 小[1-2]．随着遥感技术的发展，遥感图像的空间分辨率不断提高，如国外IKONOS、WorldView、GeoEye-2、我国高分2号等卫星的空间分辨率都达到了亚米级．对分辨率要求的提高，使得卫星微角振动成为影响航天相机成像质量的关键因素[3-4]．

为了补偿微角振动造成的像质下降，需要对图像运动模糊机理和补偿方法进行深入研究．目前，运动模糊图像的补偿方式可分为实时稳像和后期算法补偿两种．实时稳像系统复杂度高，对角振动测量和控制精度的要求都较高，并且会增加航天相机的体积和质量．而后期算法补偿虽然无法实现运动模糊的实时补偿，但实现成本低，仅需要航天相机的姿态角数据便可完成补偿，是补偿图像运动模糊的有效手段．

进行模糊图像后期算法补偿的前提是获得准确的航天相机姿态角先验信息．目前，航天相机的微角振动测量方法主要有陀螺仪[5]、线加速度计[6]和角运动传感器等．其中，以动力调谐陀螺仪、液浮陀螺仪为代表的传统陀螺仪测量精度较高，但其工作带宽一般小于20Hz，无法敏感高频角扰动．以激光陀螺仪为代表的光学陀螺仪精度较高，可达微弧度量级，带宽高500Hz，但其质量和体积较大[7-8]．线加速度计需要多个加速度计进行组合测量，这对加速度计的测量精度和安装位置精度都提出了较高的要求，并且二次积分时会导致高频误差的累积．目前，运用在卫星上的角运动传感器主要有基于流体旋转差动感应式(fluid-rotor differential induction，FDI)的角位置传感器和基于磁流体动力学(magnetohydrodynamics，MHD)的角运动传感器两种[9]．基于FDI原理的角位置传感器内部含有运动部件，传递函数复杂，测量精度依赖于内部检测元件的性能．相比FDI，基于MHD原理的角运动传感器工作原理简单，兼具测量频带宽(1～1000Hz)、精度高、低交叉轴灵敏度、内部无机械运动部件、可靠性高等优势[9-10]，适用于航天相机姿态角的测量，已在航天器姿态测量、视轴稳定及图像的运动补偿等方面取得广泛应用[11-12]．

MHD角速度传感器是由美国Bluehalo公司从20世纪80年代开始研究的，所研发的型号中ARS-24精度最高，但体积和质量都较大．针对微角振动测量和抑制系统的需求，先后研发的型号有ARS-12、14、15、16等，且已经在国外图像补偿领域取得应用．2006年，日本发射的“先进陆地观测卫星”使用了3个Bluehalo公司研制的ARS-12G型MHD角速度传感器正交安装，并与低频陀螺仪的输出数据进行融合，解决了仅依靠陀螺仪低频数据无法补偿的图像条纹噪声问题[13-14]．国内自2011年起，先后有兰州空间技术物理研究所、天津大学和上海交通大学开展了MHD角速度传感器基础理论以及相关型号的研发[8,15-16]．受到国内发展水平的限制，利用MHD角速度传感器测量航天相机角振动并进行运动模糊图像复原的研究尚鲜见报道．

本文首先推导了面阵相机在微角振动环境下成像时的像移模型，给出了基于MHD角速度传感器测量数据的点扩散函数(point spread function，PSF)构建方法；然后采用课题组自行研制的MHD角速度传感器搭建了微角振动环境下的模拟成像系统，在垂直于光轴方向加载微角振动干扰，并采集模糊图像．最后采用调制传递函数(modulation transfer function，MTF)对基于全变差(total variation，TV)正则化图像复原算法的复原结果进行评价．

1 基于MHD角速度传感器的PSF构建

1.1 MHD角速度传感器工作原理

本文所用MHD角速度传感器实物照片如图1(b)所示，其测量带宽为2～1000Hz，质量小于200g，频率响应曲线如图2所示．

图1 MHD角速度传感器工作原理和实物照片

1.2 像移模型分析

将面阵相机的成像过程看作小孔成像，以透镜组的光心为坐标原点，建立相机坐标系，如图3所示，其中轴与相机光轴重合．相机绕轴转动时，像点在焦平面上做，相同角振幅下，对像质的影响远远小于绕另外两个轴旋转时产生的影响. 绕轴的角振动会产生水平方向上的像移，绕轴的角振动则会导致竖直方向上的像移．考虑到两者的分析方法相同，本文仅对相机绕轴转动时引起的像移进行分析和补偿．

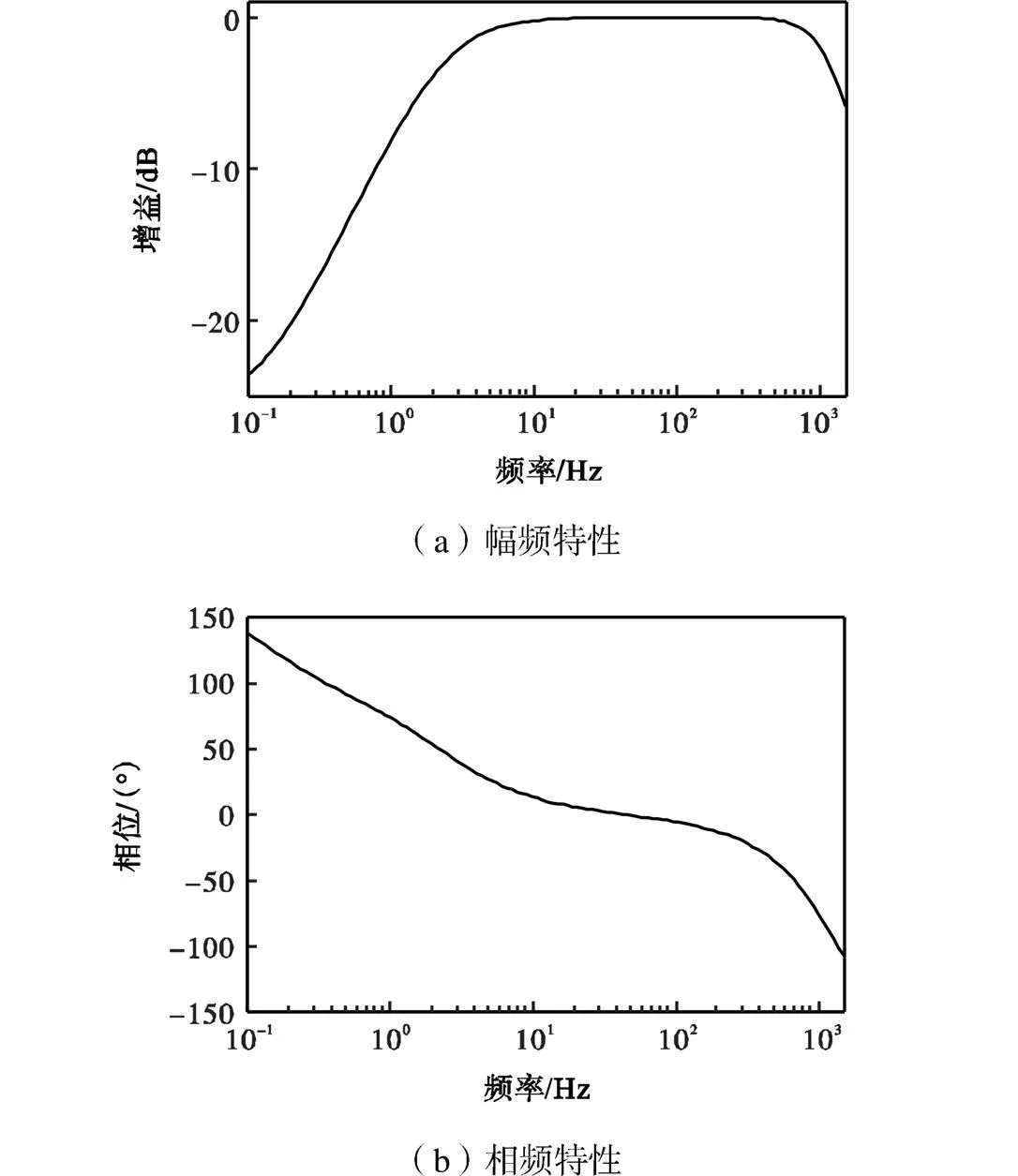
图2 MHD角速度传感器频率响应曲线

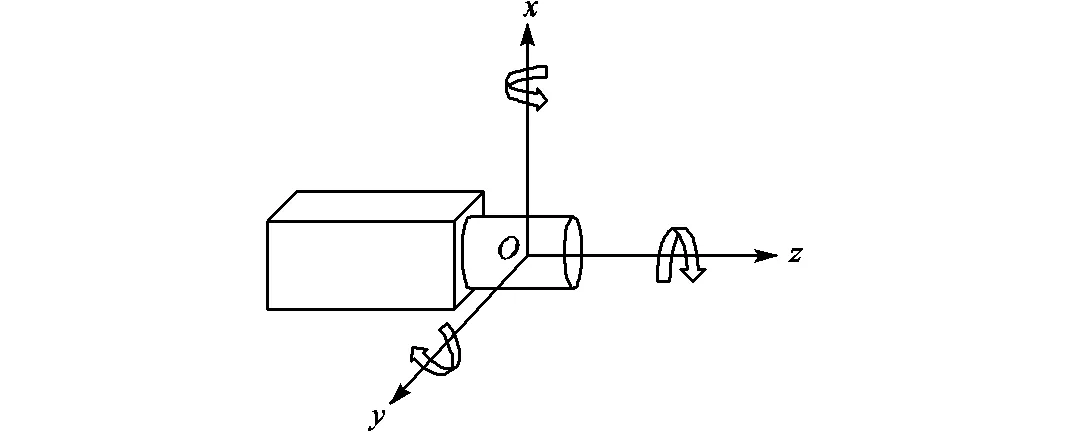
图3 以光心为原点建立的坐标系

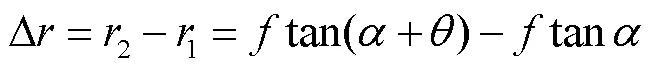
根据三角函数公式可得

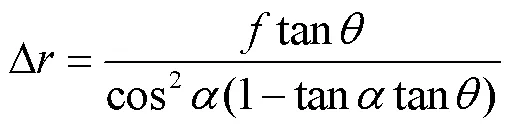
由式(2)可以看出，角振动引起的像移不仅与转动角度和焦距有关，还与物点和光轴夹角有关，图像边缘受到的影响比中心更大．

1.3 点扩散函数的构建

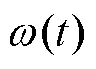
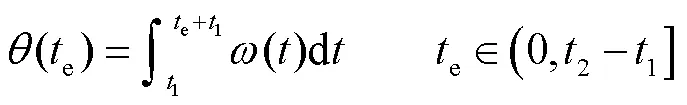
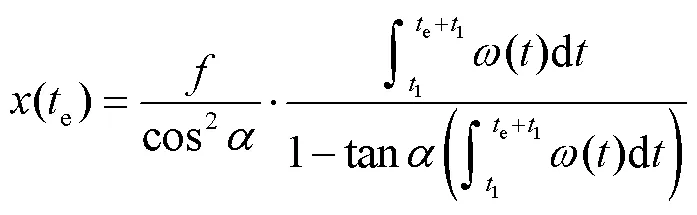
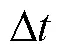
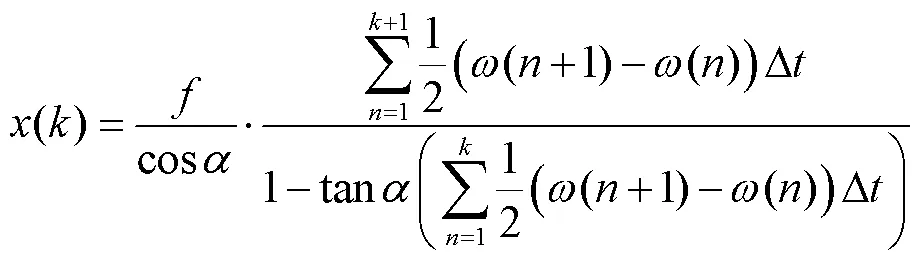
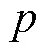
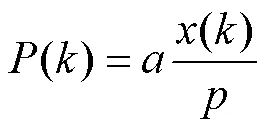
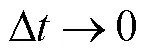
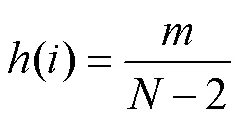
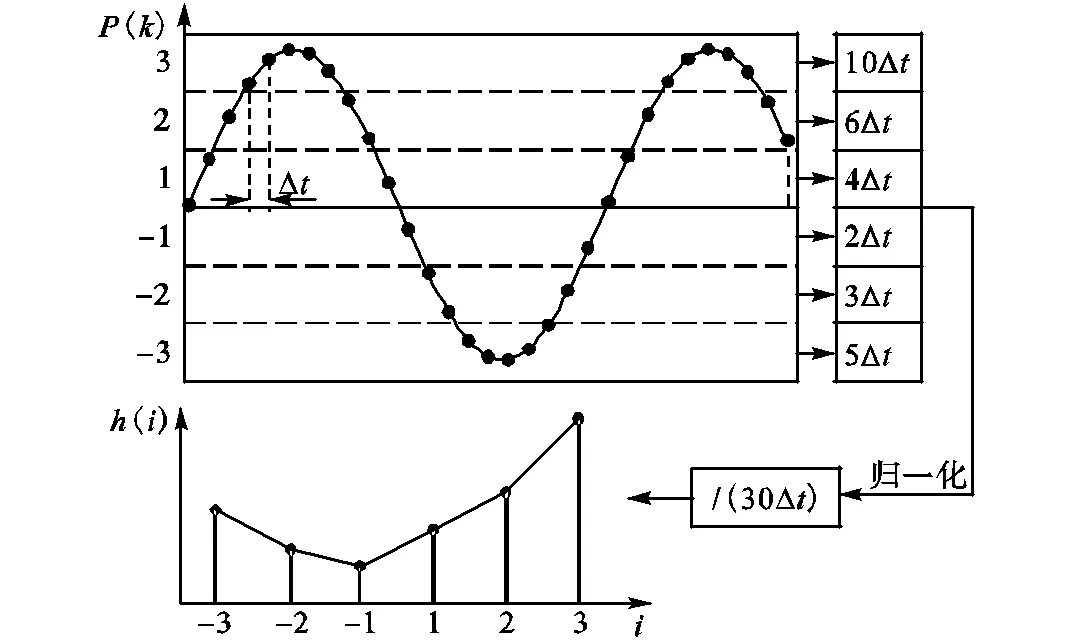
图5 通过统计采样间隔构建PSF

2 实验设计

本节通过设计实验，模拟面阵相机受到微角振动干扰时的成像过程，并对拍摄到的模糊图像进行复原．实验流程如图6所示，角振动源受到正弦激励后，会产生一个正弦角振动，成像系统受到角振动的影响，成像模糊．使用MHD角速度传感器测量成像系统所受角振动，积分得到角位移，并进一步计算像移轨迹，构建PSF．最后使用图像复原算法进行模糊图像复原，并对复原图像和模糊图像进行MTF分析，评价补偿效果．

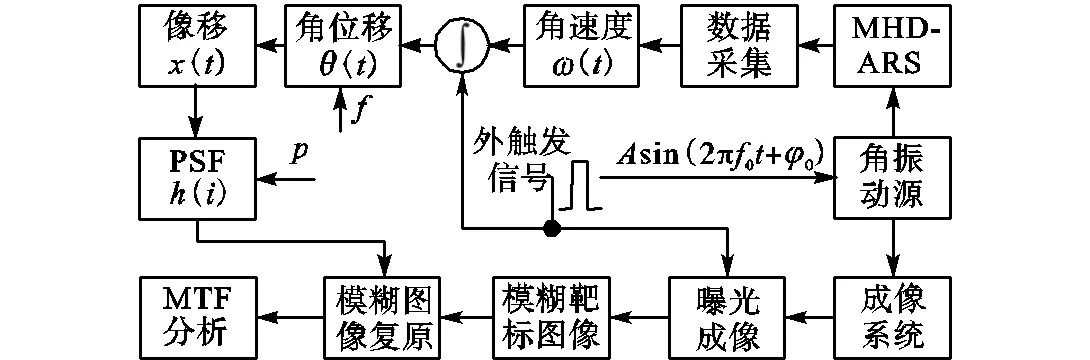
图6 实验方案流程

2.1 实验系统

实验系统的模型如图7(a)所示，实物图如图7(b)所示．该实验系统中，成像设备为面阵工业相机，相关参数列于表1．

图7 实验系统

表1 面阵相机相关参数

Tab.1 Parameters of the area scan camera

实验中选用的角振动激励源是105-AVT单轴高频角振动系统(简称角振动台)，无负载时，该角振动台可以提供5～2500Hz、转角范围±5°的角振动．面阵相机和MHD角速度传感器刚性固连在角振动台上，当上位机给角振动台一个单频正弦激励信号时，角振动台发生转动，同时MHD角速度传感器持续输出相机角速度，并由16位高性能NI数据采集卡进行采集后，传送至上位机．系统稳定运行后，相机开始曝光，对靶标成像，得到模糊靶标图像，并传输至上位机，实验靶标采用ISO 12233标准分辨率测试卡.

为了能准确得到曝光的起始时刻，相机采用外触发采集模式，触发信号由上位机给出．为了使靶标在不同曝光时长内都能成明亮的像，在靶标后面增加一个亮度可调的面阵LED光源进行照明．同时为了减少外界振动对实验的干扰，以上设备全部安装在气浮隔振平台上．

2.2 图像复原算法和质量评价方法

2.2.1 TV正则化算法

图像复原问题是数字图像处理领域的重要研究课题．1992年，Rudin等[17]将Tikhonov正则化中的图像2范数约束更改为图像梯度和约束，提出了著名的ROF模型用于图像去噪．该算法能够在去除噪声的同时保护图像边缘细节[18]，后被大量用于模糊图像的复原中．

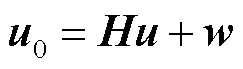
TV正则化复原优化算法将图像复原问题转换为求解无约束最优化问题，即

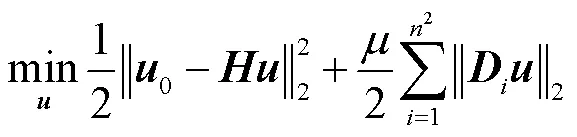
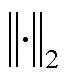
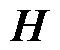
为了快速求解该最优化问题，已有诸多学者提出了多种算法，如分裂Bregman算法[19]、快速TV(fast total variation deconvolution，FTVd)算法[20]等，这些算法都致力于减少计算复杂度，提高运行速度．其中分裂Bregman算法[19]通过拆分算子将复杂的优化问题拆分为多个子问题，然后应用Bregman迭代法求解多个最优化子问题．

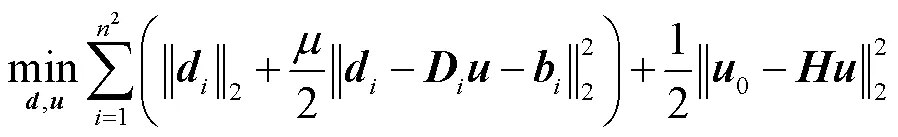
式(9)可分解为对以下2个子问题进行求解.

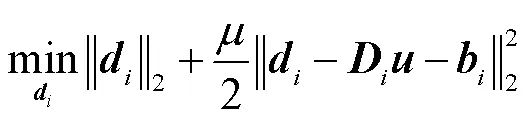
根据二维收缩定理可得出式(11)的闭合解为

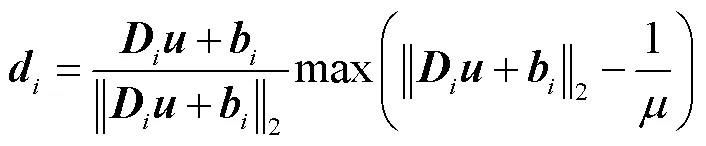
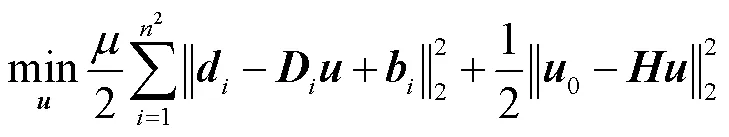
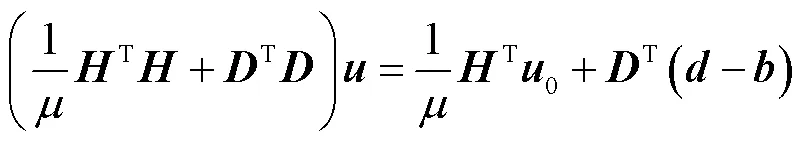
分裂Bergman算法通过以下步骤迭代求解最优化问题.

2.2.2 图像质量评价方法

图像的MTF可以用来评价光学系统的成像质量，它能反映出成像系统对不同空间频率目标的解像力[21-23]．传统的MTF测量方法需要分别测量成像系统对不同空间频率黑白线条的解像力，过程复杂，花费时间长．而倾斜刃边(slanted edge，SE)法只需要选取一张图像上的一个倾斜边缘，通过过采样细化刃边的灰度值变化，得到边缘扩散函数(edge spread function，ESF)，将ESF微分可得到线扩散函数(line spread function，LSF)，LSF的傅里叶变换即为完整的MTF曲线，过程如图8所示．ISO 12233标准分辨率测试卡上提供了一个小角度的倾斜边缘用于MTF 检测．

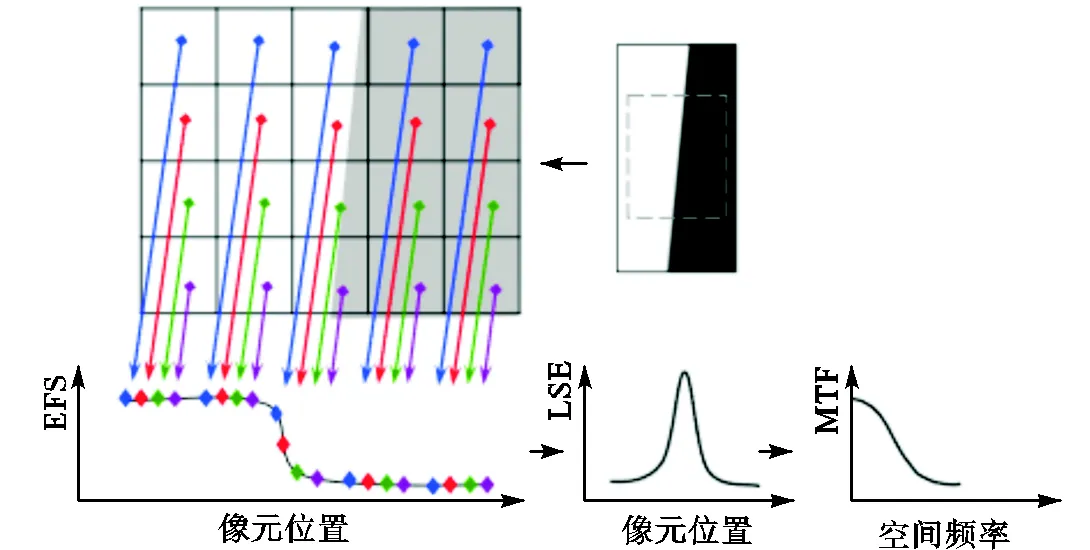
图8 倾斜刃边法获取MTF过程

3 实验结果与分析

3.1 图像复原结果

为了验证TV正则化图像复原算法对微角振动导致的模糊图像的复原效果，选择维纳滤波算法和RL(Richardson-Lucy)算法与TV正则化算法进行比较，这两种经典的非盲复原算法分别在频域和空域取得了理想的图像复原结果．给角振动台施加一个32Hz的正弦激励，产生10个像元的像移，采集模糊图像．使用3种方法对同一模糊图像进行复原，噪声方差取0.001，RL算法循环20次，复原结果如图9所示．从图9中可以看出：维纳滤波复原图像可分辨出文字和数字轮廓，但噪点被放大，图像颗粒感严重；而RL算法出现明显振铃现象；TV正则化算法能够抑制噪声，平坦区域未出现明显振铃，数字轮廓和文字恢复较好．综上，基于TV正则化的图像复原优化算法在本实验中的表现优于其他两种算法，故实验中选择TV正则化算法作为模糊图像复原的方法．

限于角振动台的带负载能力，仅对20～300Hz的角振动进行模拟．给高频角振动台施加20～300Hz的单频正弦激励，采集不同频率下的模糊图像，并使用TV正则化优化算法进行图像复原．限于篇幅，文中仅给出角振动频率为40Hz、110Hz、233Hz以及267Hz的图像复原结果，实验参数列于表2，模糊图像和复原图像如图10～图13所示．

图9 32Hz正弦激励下的不同算法图像复原结果

表2 40 Hz、110 Hz、233 Hz、267 Hz角振动实验条件

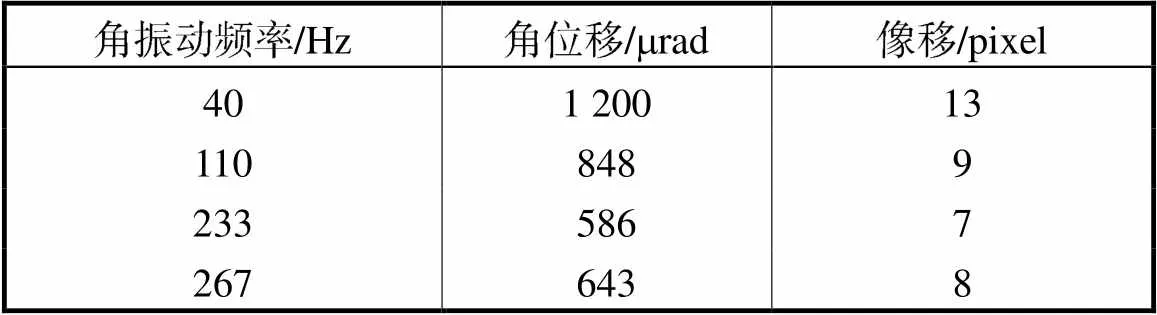
Tab.2 Experimental conditions at 40，110，233，and 267Hz angular vibrations

从视觉上判断，40Hz、110Hz、233Hz和267Hz 4种频率的正弦角振动都使模糊图像出现了“重影”现象，像质退化严重．利用TV复原算法复原后，重影消失，边缘轮廓清晰分明，图像的对比度和锐度都有了明显的提升，图像整体质量得到明显改善．

3.2 图像质量评价与结果分析

为了更进一步评价图像的复原质量，使用倾斜刃边法获得40Hz、110Hz、233Hz和267Hz频率下静态图像、模糊图像和复原图像的MTF曲线，如图14所示．从图14中可以看出，复原图像的MTF曲线整体高于模糊图像的MTF曲线，且与静态图像的MTF曲线接近，特别在低频部分，复原图像的 MTF 曲线甚至高于静态图像，图像轮廓得到了更好的复原，而高频部分下降较快，截止频率低于静态图像，但仍在可接受范围内．

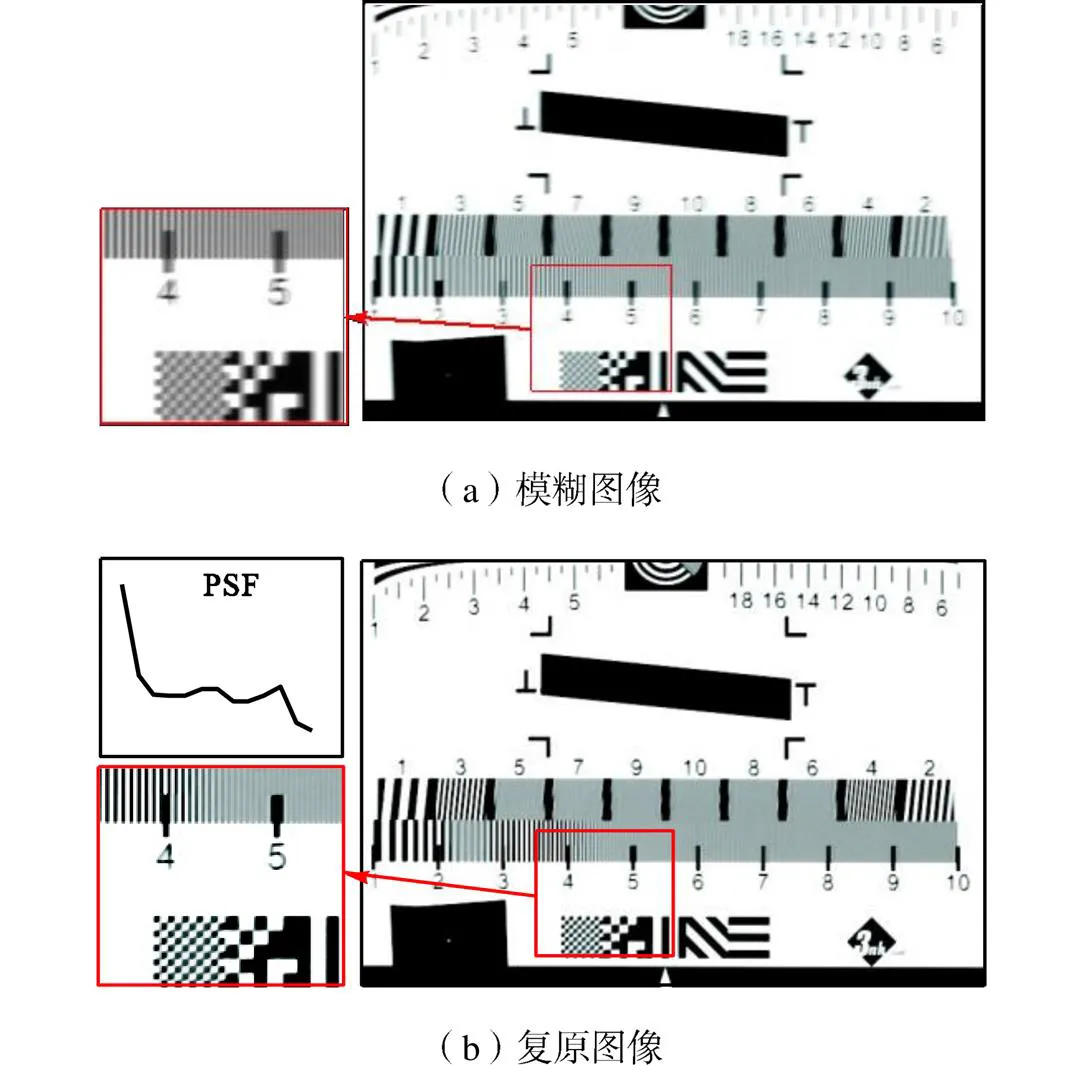
图10 40Hz正弦激励下的图像复原结果(a＝1.00)

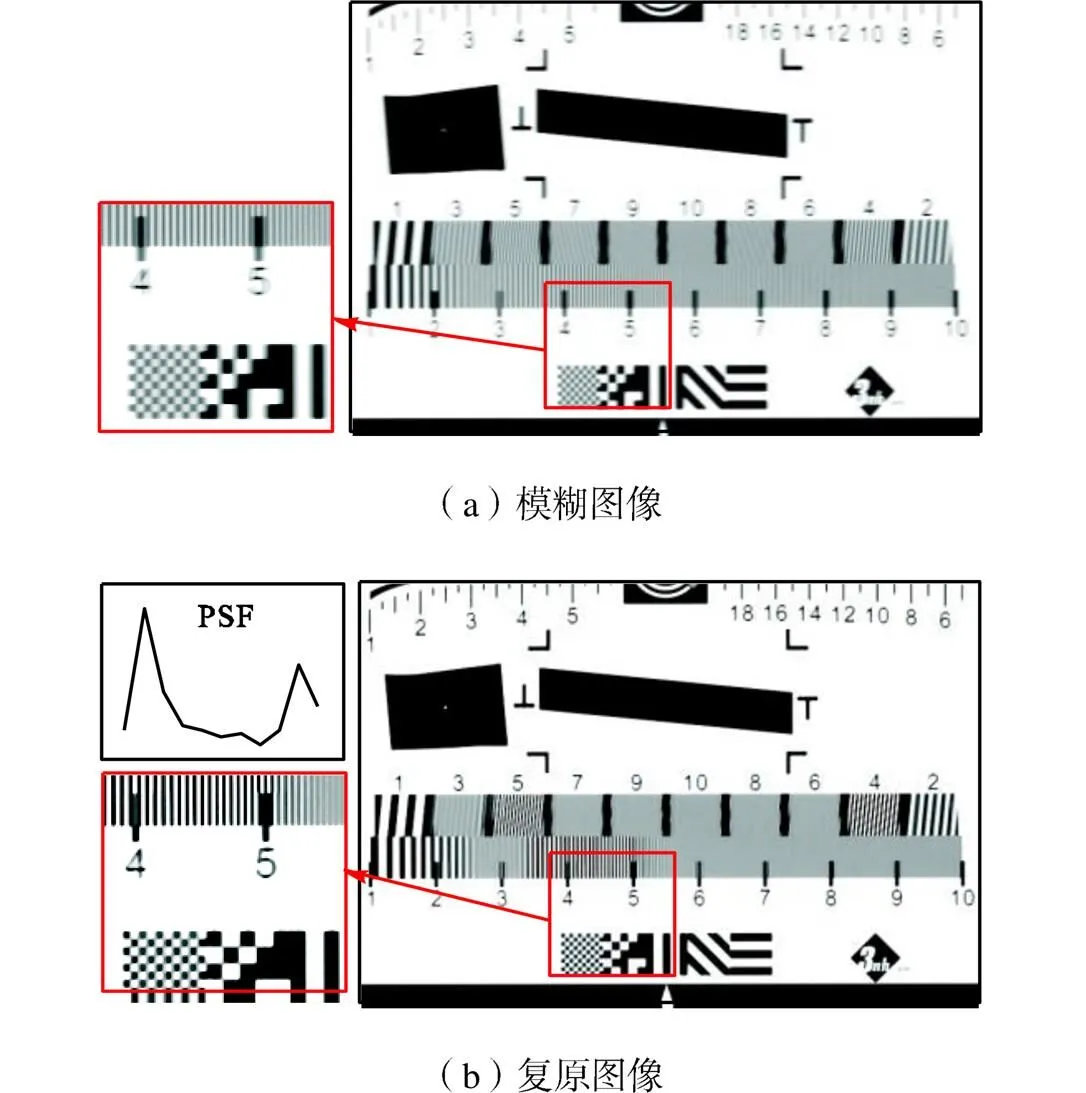
图11 110Hz正弦激励下的图像复原结果(a＝1.38)

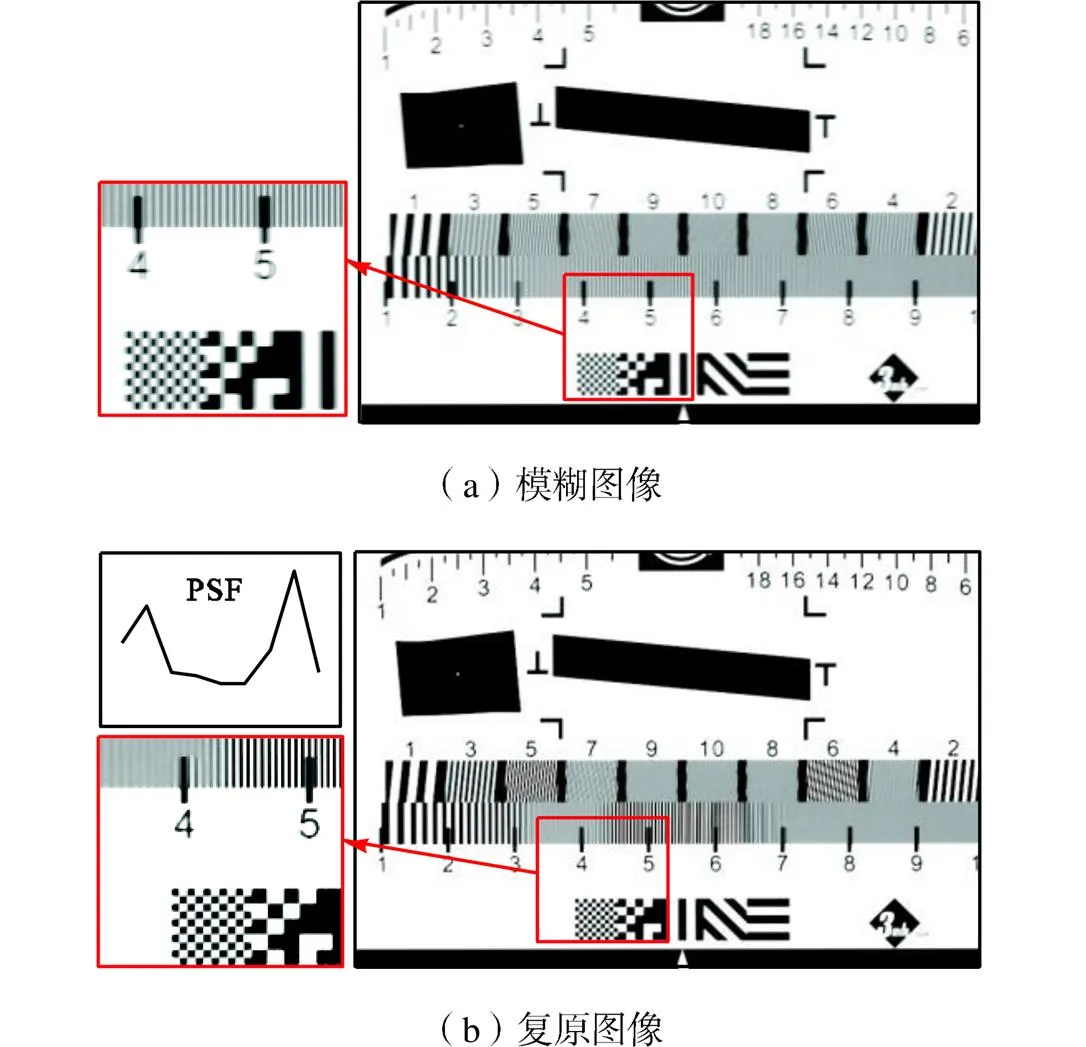
图12 233Hz正弦激励下的图像复原结果(a＝1.15)

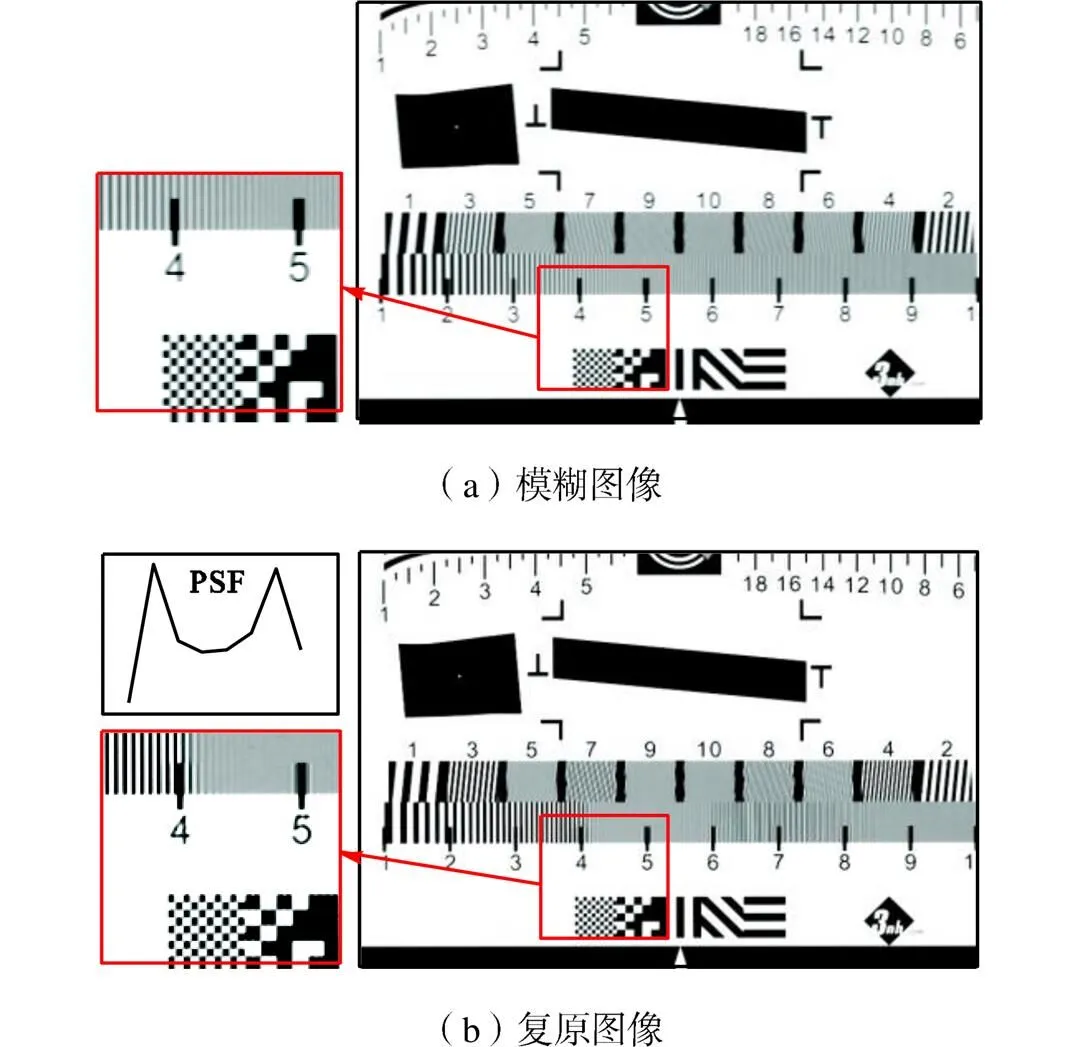
图13 267Hz正弦激励下的图像复原结果(a＝1.38)

在MTF分析中，图像MTF曲线与坐标轴围成的面积称为调制传递函数面积(MTFA)，是一个用来描述光学系统整体分辨能力的物理量．为了进一步量化评价图像质量的改善程度，将上述MTF曲线进行积分，积分范围分别为0～150cycle/mm(奈奎斯特频率)，所得结果列于表3．

从表3中可以看出，40Hz、110Hz、233Hz、267Hz的角振动产生的像移使成像系统的整体图像质量下降严重，图像复原后，复原图像整体质量与静态图像的整体质量相近，且高于模糊图像的整体质量2倍以上，复原效果良好，与直接观察得出的结论一致．

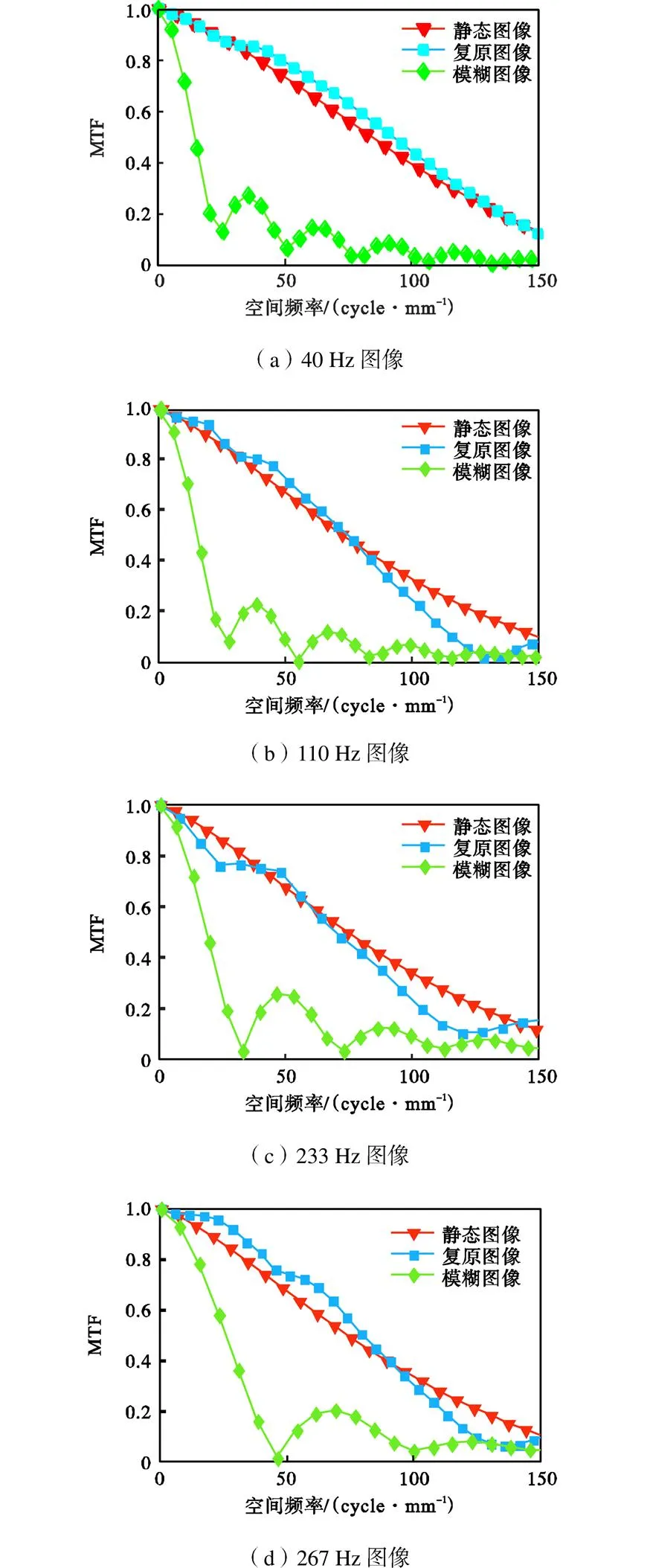
图14 40Hz、110Hz、233Hz和267Hz静态图像、模糊图像和复原图像的MTF曲线比较

表3 40Hz、110Hz、233Hz、267Hz角振动下的MTFA

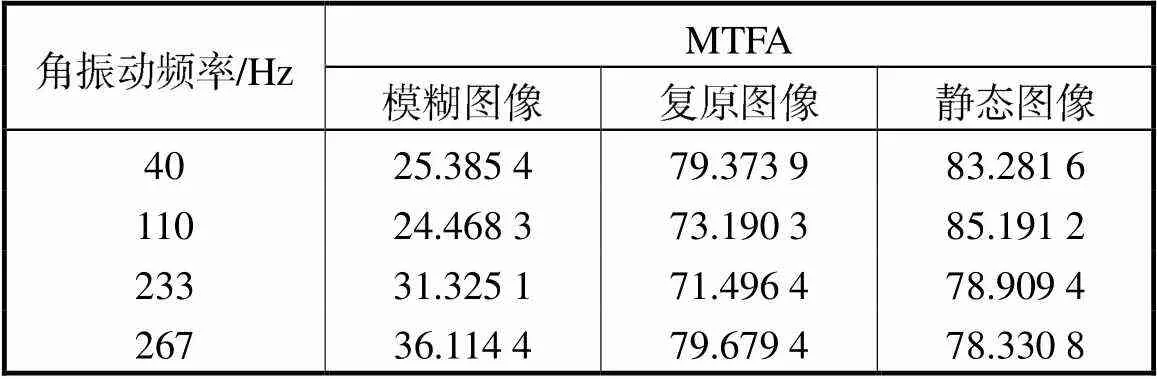
Tab.3 MTFA at 40，110，233，and 267Hz angular vibrations

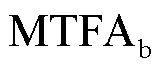
表4 不同角振动频率下的实验结果

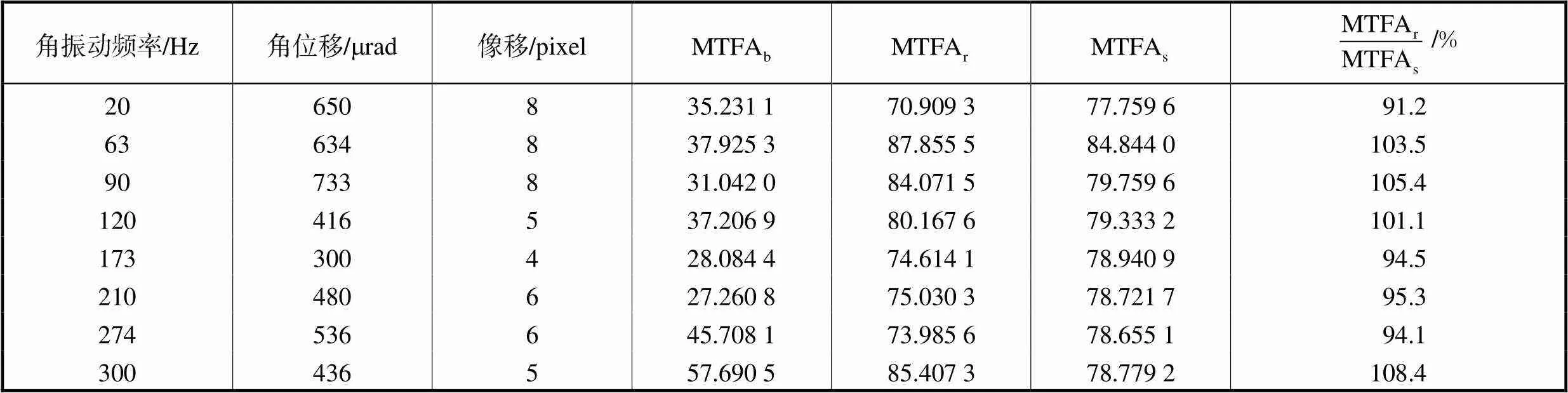
Tab.4 Experimental results at different angular vibration frequencies

对多个角振动频率下模糊图像的复原结果进行比较，可以看出，对20～300Hz角振动导致的图像模糊，图像复原算法能进行较好的复原，复原后的图像整体质量都有了一定的提升．

为验证提出的方法在各频点的重复性，任意选取20～300Hz内的10个频点，保持某一频点的激励幅值不变，进行模糊成像实验，重复采集该频点的10张模糊图像．分别对每一个频点的10张模糊图片进行图像复原，并对复原图像、模糊图像和静态图像进行MTF分析，计算MTFA值．

限于篇幅，仅给出175Hz角振动激励条件下的重复实验结果．在175Hz频率下，像点产生7个像元的像移，静态图像MTFA为117.63，其10次模糊图像结果MTFA和复原图像MTFA列于表5．实验过程中，曝光时长确定，但曝光开始时刻的角振动相位无法控制，使得曝光时间内测得的角振动在非整周期部分存在随机性，导致点扩散函数稍有差别，但像移的最大幅值未发生变化．

从表5的实验结果可以看出，在同一角振幅下，尽管曝光开始时刻角振动相位的随机性使模糊图像的MTFA出现了波动，但复原图像的MTFA达到了静态图像MTFA的90%以上，可以证明本文提出的方法在各频点处重复实验时，都能取得较好的效果．

表5 175 Hz角振动重复性实验结果

4 结 语

随着遥感技术的发展，对航天相机的空间分辨率要求越来越高，微角振动引起的像移对像质的影响不可忽视．本文提出使用MHD角速度传感器测量航天相机的微角振动，并通过基于TV正则化的图像复原算法完成模糊图像复原，提高图像质量．通过搭建模拟成像系统，模拟了面阵相机受到单频正弦微角振动时的成像过程，并使用MHD角速度传感器对成像系统受到的微角振动进行探测．图像复原结果表明：20～300Hz实验频率下，复原后图像的MTFA都提高到了静态图像的90%以上，图像质量得到了明显提高．基于MHD角速度传感器探测相机角振动的图像复原方法能够有效地补偿微角振动造成的图像运动模糊．

限于实验条件，本文仅对绕相机轴的角振动进行了模拟，但实际成像时，同时存在绕其他两轴的角振动，同样需要进行测量与补偿．为了更好地复原图像，需要进一步使用多个MHD角速度传感器对绕相机3个轴的角振动进行测量，并构建更准确的PSF.目前使用的TV正则化算法虽然方法成熟，噪声抑制能力强，但运算量大、运行速度过慢，仍需寻找更快速的复原算法，实现实时图像补偿．并且在算法运行过程中，尚有需要人工干预部分，应进一步完善文中提出的方法，构建能自动寻找最优参数的自适应复原算法．

［1］ 孙 阳，薛栋林，郑立功，等. 航天器平台在轨振动对遥感成像质量的影响[J]. 光学技术，2013，39(6)：553-558.

Sun Yang，Xue Donglin，Zheng Ligong，et al. Satellite platform on-orbit vibration’s influence to image quality of remote sensing[J]. Optical Technique，2013，39(6)：553-558(in Chinese).

［2］ 霍红庆，马勉军，李云鹏，等. 卫星微角颤振高精度测量技术[J]. 传感器与微系统，2011，30(3)：4-6，9.

Huo Hongqing，Ma Mianjun，Li Yunpeng，et al. High precision measurement technology of statellite’s angle micro vibration[J]. Transducer and Microsystem Technologies，2011，30(3)：4-6，9(in Chinese).

［3］ Lin Li，Li Wang，Li Yuan，et al. Micro-vibration suppression methods and key technologies for high-precision space optical instruments[J]. Acta Astronautica，2021，180：417-428.

［4］ Roques S，Jahan L，Rougé B，et al. Satellite attitude instability effects on stereo images[C]//2004 IEEE International Conference on Acoustics，Speech，and Signal Processing. Piscataway，USA，2004：477-480.

［5］ Fan Mo，Xie Junfeng，Liu Yuxuan. Vibration model of Ziyuan3 satellites considering frequency changing[J]. Journal of Vibration and Control，2020，26(17/18)：1484-1502.

［6］ Zhang Guo，Guan Zhichao. High-frequency attitude jitter correction for the Gaofen-9 satellite[J]. The Photogrammetric Record，2018，33(162)：264-282.

［7］ 边志强，张 健，牛升达. 惯性技术在航天器中的应用及展望[C]// 前沿技术与惯性技术的融合与应用研讨会文集. 大连，中国，2021：428-438.

Bian Zhiqiang，Zhang Jian，Niu Shengda. The application and prospect of inertial technology in spacecraft[C]// Proceedings of the Symposium on Integration and Application of Frontier Technology and Inertial Technology. Dalian，China，2021：428-438(in Chinese).

［8］ 吴文韬，李醒飞，刘 帆，等. 一种卫星微角振动高精度测量方法[J]. 航天器工程，2020，29(1)：16-22.

Wu Wentao，Li Xingfei，Liu Fan，et al. A high-precision measurement method for satellite micro-angular vibration[J]. Spacecraft Engineering，2020，29(1)：16-22(in Chinese).

［9］ 霍红庆，马勉军，李云鹏，等. MHD 角速度传感器在航天任务中的应用[J]. 真空与低温，2011(2)：114-120.

Huo Hongqing，Ma Mianjun，Li Yunpeng，et al. The application of MHD angular rate sensor in aerospace[J]. Vacuum and Cryogenics，2011(2)：114-120(in Chinese).

［10］ Laughlin D R. A magnetohydrodynamic angular motion sensor for anthropomorphic test device instrumentation[J]. SAE Transactions，1989：1648-1682.

［11］ Laughlin D R，Smith D. Development and performance of an angular vibration sensor with 1—1000 Hz bandwidth and nanoradian level noise[C]// Free-Space Laser Communication and Laser Imaging. San Francisco，USA，2002：208-214.

［12］ Lee D V，Velinsky S A. Analysis and experimental verification of a three-dimensional noncontacting angular motion sensor[J]. IEEE/ASME Transactions on Mechatronics，2007，12(6)：612-622.

［13］ Iwata T. Precision geolocation determination and pointing management for the advanced land observing satellite(ALOS)[C]// 2003 IEEE International Geoscience and Remote Sensing Symposium. Piscataway，USA，2003：1845-1848.

［14］ Iwata T，Kawahara T，Muranaka N，et al. High-bandwidth attitude determination using jitter measurements and optimal filtering[C]// AIAA Guidance，Navigation，and Control Conference. Chicago，USA，2009：6311.

［15］ 吴建铭，李建勋，张明举. 角随机颤振传感器导电流体环数学模型推导[J]. 测控技术，2018，37(7)：69-73.

Wu Jianming，Li Jianxun，Zhang Mingju. Mathematical model of conducting fluid ring for freedom angular flutter speed sensor[J]. Measurement & Control Technology，2018，37(7)：69-73(in Chinese).

［16］ 周海佳，李得天. MHD传感器敏感结构地面温度特性数值分析[J]. 西北工业大学学报，2018，36(增)：110-116.

Zhou Haijia，Li Detian. Numerical analysis of temperature sensitivity for sensitive mechanism in MHD sensor on ground[J]. Journal of Northwestern Polytechnical University，2018，36(Suppl)：110-116(in Chinese).

［17］ Rudin L I，Osher S，Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D：Nonlinear Phenomena，1992，60(1/2/3/4)：259-268.

［18］ 张 彬，于欣妍，朱永贵，等. 图像复原优化算法[M]. 北京：国防工业出版社，2019.

Zhang Bin，Yu Xinyan，Zhu Yonggui，et al. Optimal Algorithm for Image Restoration[M]. Beijing：National Defense Industry Press，2019(in Chinese).

［19］ Osher S，Burger M，Goldfarb D，et al. An iterative regularization method for total variation-based image restoration[J]. Multiscale Modeling & Simulation，2005，4(2)：460-489.

［20］ Wang Yilun，Yang Junfeng，Yin Wotao，et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences，2008，1(3)：248-272.

［21］ 孙崇尚，王 琦，丁亚林，等. 基于倾斜刃边法航空相机像移的调制传递函数测量[J]. 光学学报，2014，34(12)：108-113.

Sun Chongshang，Wang Qi，Ding Yalin，et al. Modulation transfer function measurement of image motion of aerial camera based on slanted-edge method[J]. Acta Optical Sinica，2014，34(12)：108-113(in Chinese).

［22］ Estribeau M，Magnan P. Fast MTF measurement of CMOS imagers using ISO 12233 slanted-edge methodology[C]// Optical Systems Design. St Etienne，France，2003：243-252.

［23］ Wong S，Jassemi-Zargani R. Predicting Image Quality of Surveillance Sensors[M]. Ottawa：Defence Research and Development Canada，2014.

Blurred Image Restoration of Area Scan Camera Based on Magnetohydrodynamics Angular Rate Sensor

Zhao Ling1, 2，Fei Rong1，Li Xingfei1, 2，Tuo Weixiao1, 2，Xing Weida1

(1. State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China；2. Taihu Laboratory of Deep Sea Technology and Science，Wuxi 214123，China)

Wide-band and low-amplitude micro-angular vibrations are common in orbiting satellite platforms. With the continuously improving requirements for the detection capability of aerospace cameras and the spatial resolution of remote sensing images，micro-angular vibrations can have a serious impact on the imaging quality of a satellite optical system. To solve the problem of image blur caused by high-frequency micro-angular vibrations，a magnetohydrodynamics(MHD)angular rate sensor was proposed to measure the micro-angular vibrations of an area scan camera by constructing a point spread function based on the angular motion information of the area scan camera and using the image restoration algorithm based on total variation regularization for image restoration，thereby improving the image quality. First，the reasons for the image movement caused by the micro-angular vibration interference of the aerospace camera were analyzed，the image movement model was developed，and the point spread function was constructed based on the movement trajectory of the image point on the focal plane. Second，an experimental system was designed to simulate the imaging process of the aerospace camera in a micro-angular vibration environment，and the single-frequency sinusoidal micro-angular vibration disturbances were applied perpendicular to the optical axis and detected using the MHD angular rate sensor. Finally，the blurred image was restored using the total variation regularization image restoration algorithm，and the restoration image quality was evaluated based on the modulation transfer function. The experimental results demonstrated that when the micro-angular vibration frequency lay between 20 and 300Hz and the resulting image movement was less than 13 pixels，the modulation transfer function area of the restored image could be increased to more than 90% of the static image with clear image details and a significantly improved contrast. After repeating the experiments on the same micro-angular vibration frequency several times，the image restoration results confirmed a good repeatability of the proposed method.The relevant experimental results showed that the combination of the micro-angular vibration measurement method based on the MHD angular rate sensor and the image restoration algorithm can significantly improve the imaging quality of the aerospace camera.

magnetohydrodynamics(MHD) angular rate sensor；micro-angular vibration；image quality；image restoration

10.11784/tdxbz202205051

TP751.1

A

0493-2137(2023)08-0796-11

2022-05-27；

2022-10-02.

赵 苓（1984—  ），女，博士，副教授，lingzhao84@126.com.Email：m_bigm@tju.edu.cn

李醒飞，lixf_mhd@163.com.

国家自然科学基金资助项目(61733012，62203322)；深海技术科学太湖实验室“揭榜挂帅”项目(2022JBGS03001)；中国博士后科学基金资助项目(2022M712372).

the National Natural Science Foundation of China(No.61733012，No.62203322)，the Enlisting and Leading Program of the Taihu Laboratory of Deep Sea Technology and Science(No.2022JBGS03001)，China Postdoctoral Science Foundation (No.2022M712372).

(责任编辑：孙立华)