防淤积型透空式防波堤波浪爬高试验及预测研究

于通顺，赵学文，唐俊辉，张振宇，陈星羽

防淤积型透空式防波堤波浪爬高试验及预测研究

于通顺1，赵学文1，唐俊辉2，张振宇1，陈星羽1

(1. 中国海洋大学工程学院，青岛 266100；2. 中国电力工程顾问集团东北电力设计院有限公司，长春 130000)

波浪爬高是防波堤堤顶高程设计和预估工程造价的重要影响因素．以防淤积型透空式防波堤为研究对象，采用1∶10的模型比尺，在64组不同工况下开展防波堤的物理模型爬高试验，并记录了不同工况下防波堤迎浪侧的最大波浪爬升高度，探究了防波堤的波浪爬升特征．分别运用多项式回归方法、速度水头方法与M5模型树算法并结合物理模型试验波浪爬高结果，发展透空式防波堤波浪爬高的预测公式．利用统计参数对3种方法发展的预测公式进行对比分析．结果表明：透空式防波堤背浪侧的波面变化滞后于迎浪侧，其最大波浪爬高小于迎浪侧，防波堤具有良好的消波效果；采用多项式回归方法与速度水头方法发展的预测公式能够在一定程度上实现对防波堤波浪爬高的预测，前者仅考虑了波高而忽略了其他波浪条件及防波堤结构参数对波浪爬升高度的影响，后者对波浪爬高的预测结果与试验值偏差较大，二者在实际应用过程中都存在一定的局限性；M5模型树算法发展的波浪爬高预测公式利用无量纲参数综合了各项波浪要素以及防波堤的结构参数等，拥有良好的统计指数，能够更好地预测透空式防波堤的波浪爬高，具有较高的实际应用价值．

透空式防波堤；波浪爬高；物理模型试验；多项式回归方法；速度水头；M5模型树；统计参数；预测公式

防波堤是港口工程中常见的防浪设施，可以阻拦港池外的波浪能进入港池内部，改善港池内水域的泊稳条件[1]．蓝色海湾生态海堤项目拟打造集水利、生态、安全于一体的综合防潮屏障，透空式防波堤作为新兴的防波堤结构形式，具有较高的应用价值与发展前景[2-4]．透空式防波堤主要由上部的挡板类结构与下部的支撑结构组成，不仅可以消除波浪能量，还可以实现港池内外的水体交换，防止港池内水体污染.由于透空式防波堤水体交换过程携带部分泥沙进入港池内，港池内会发生泥沙淤积，Yu等[5]提出了一种防淤积的透空式防波堤，在单层竖直挡板的基础上增加上、下两块拦沙板，并在防波堤外海侧设置泥沙含量采集室．上拦沙板置于挡浪板后，通过实时监测防波堤外海侧的泥沙含量的方式来控制上拦沙板上、下移动，进而改变港池内外水体的交换速率，起到防止堤后泥沙淤积的作用．

对于防波堤波浪爬高效应影响的研究大多以斜坡堤为研究对象，而对透空式防波堤的波浪爬高关注较少．现有的波浪爬高经验公式能否适用于透空式防波堤的波浪爬升存疑．因此，本文以防淤积型透空式防波堤为研究对象，开展了透空式防波堤的波浪爬高模型试验，基于物理模型试验结果考查了现有波浪爬升预测公式对于透空式防波堤的适用性，进一步结合多种预测方法发展了更适合防淤积型透空式防波堤波浪爬高的预测公式，并运用统计误差指数对预测公式进行对比分析．

1 透空式防波堤波浪爬高试验设计

1.1 试验模型及布置方式

防淤积型透空式防波堤的波浪爬升试验在中国海洋大学工程水动力实验室的波流水槽完成．试验水槽长30.0m，宽0.6m，高0.9m，首端装有推板式造波机，水槽末端设置消波区域，通过消波网来削弱反射波的影响．

根据《防波堤设计与施工规范》[14]的设计要求，对于越浪不明显的直立式防波堤，其堤顶高程应为设计高水位上不小于1.25倍设计波高处．单侧挡浪结构的透空式防波堤，其挡板入水深度与水深的比值宜位于0.3～0.5．综合考虑模型试验水槽的结构尺寸、试验设备参数等性能，依据重力相似准则，透空式防波堤的模型比尺定为1∶10，各类比尺大小见表1．

图1给出了本次模型试验布置示意，沙床整体位于水槽中间位置，长、宽、高分别为7.0m、0.6m和0.2m．透空式防波堤模型置于水槽中部，模型下部埋于沙床中．模型前侧沙床长度设为3m，后侧为4m．为方便记录波面时程，将1#、2#两台波高仪分别置于模型前2.2m和1.9m处，3#、4#两台波高仪置于模型后1.8m和2.0m处．

表1 模型比尺

Tab.1 Model scales

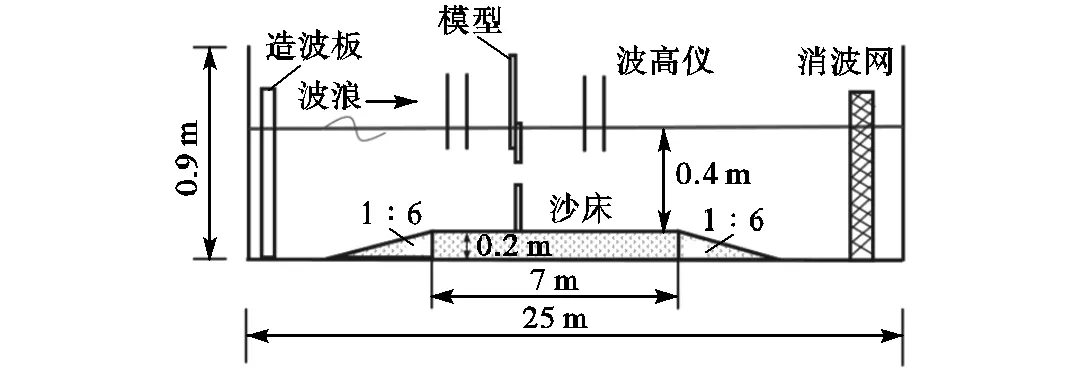
图1 模型布置示意

试验选取包含1个竖直桩及其两侧的相连防波堤作为研究对象，桩柱部分选择钢材作为设计材料，长、宽、高分别为0.06m、0.06m和0.9m，其两侧的挡板分别表示两段防波堤．试验中将桩柱两侧挡板做成整体结构，其中挡浪板长、宽、高分别为0.6m、0.02m和0.4m，上拦沙板和下拦沙板长、宽、高均分别为0.6m、0.02m和0.15m(见图2(a))．

试验过程中为控制下拦沙板的高度，将其分割成3块0.05m高的小板，通过改变拦沙板的数量来改变其高度．为防止水体从下拦沙板下侧通过，排除渗流通道对试验结果的影响，在下拦沙板下侧设置长、宽、高分别为0.6m、0.02m和0.15m的挡板，并将其埋入泥沙中．试验中所有挡板材料均为亚克力板，可插入桩柱中空缝隙中，并用螺纹杆连接，螺母固定．为防止波流作用下模型发生颤动或偏移，在桩柱下方焊接长、宽、高分别为0.15m、0.3m和0.0008m的薄板来安放模型，上部用铁块压实，并用“L”形角铁支架和“G”字夹将模型固定于水槽侧壁(见图2(b)).

图2 试验模型

1.2 试验工况

本次试验对防淤积型透空式防波堤在波浪条件下的波浪爬高开展研究，试验共计64组．表2为试验中波浪要素以及后续所用无量纲参数的取值范围.

表2 试验波浪参数与无量纲参数范围

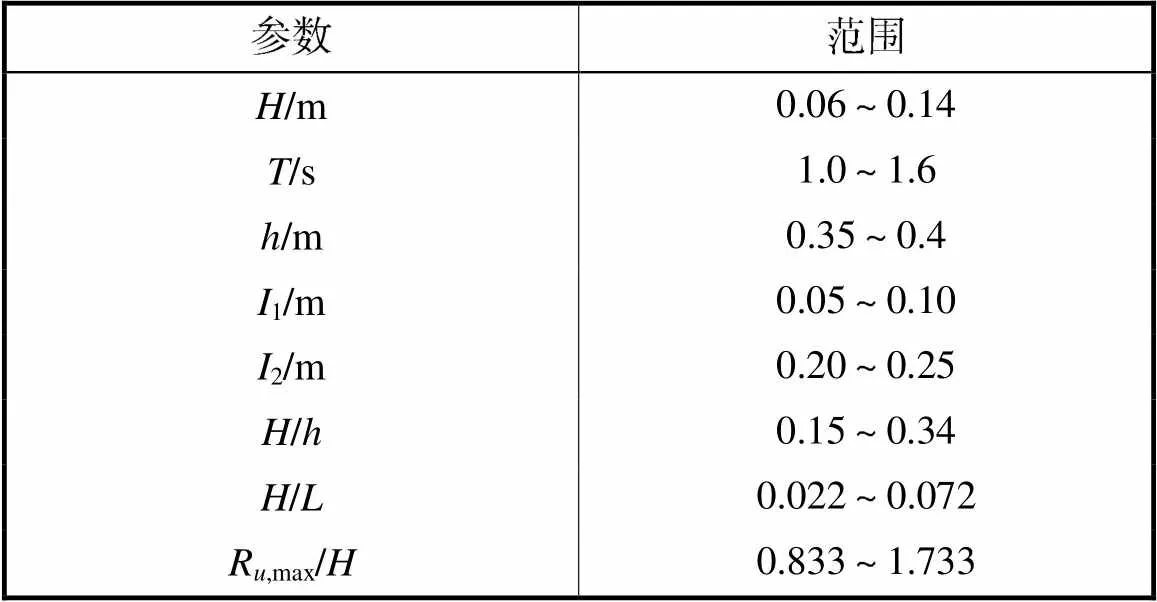
Tab.2 Ranges of experimental wave parameters and non-dimensional parameters

注：为波高；为周期；为水深；为波长；1与2分别为试验中上、下挡板与静水面之间的距离；R,max为防波堤迎浪侧波面最大爬升高度，m．

试验过程中每组工况试验重复3次并利用高清摄像仪记录波浪爬升过程．读取3次试验防波堤迎浪侧的最大波浪爬高，并取平均值作为该组工况下的最大波浪爬高值R,max．

2 试验结果与现有公式对比

2.1 试验现象

对水深0.4m、波高0.08m、周期1.6s工况下1个周期内透空式防波堤波浪表面的瞬时高程变化进行研究．当波浪到达防波堤迎浪侧时，波浪受到防波堤的阻碍作用，使得堤前水体壅高，波面由静水面(R＝0处)逐渐上升，达到最大爬升高度(R＝0.0763m处)．波面随即发生回落，到达波面最低点(R＝-0.04m处)．防波堤迎浪侧波面回落过程中伴随有浪花飞溅，发生明显的波浪破碎现象．从防波堤波浪爬升过程中可以看出，防波堤背浪侧的波面变化滞后于迎浪侧波面，最大波浪爬高小于迎浪侧．这是由于防波堤的阻碍作用使得传递到透空式防波堤后侧的波浪能量减小，最大波浪爬升高度随之减小．表3为本次试验的全部工况与迎浪侧最大波浪爬高结果．

表3 透空式防波堤波浪爬高试验工况及结果

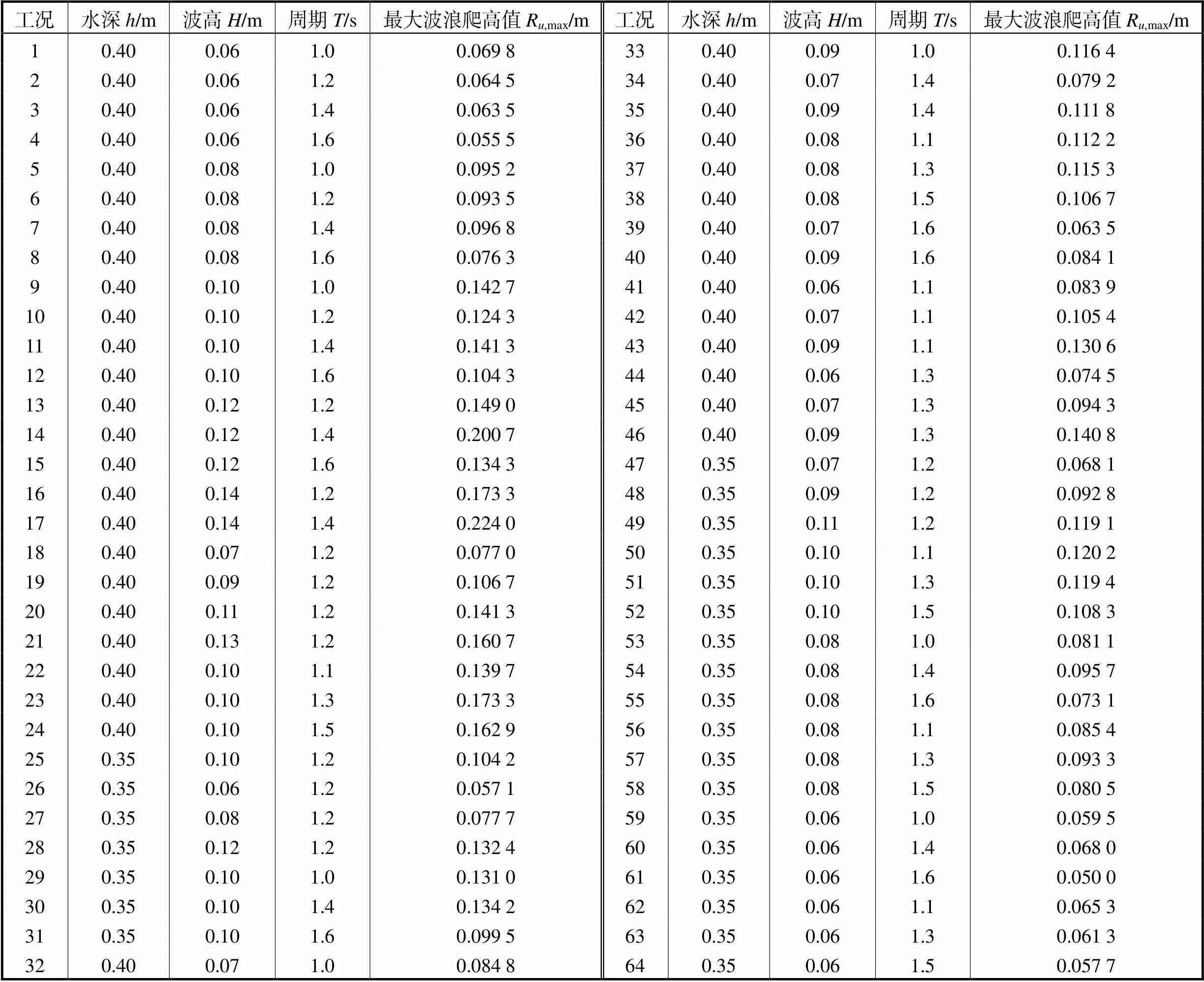
Tab.3 Wave run-upexperimental conditions and results of permeable breakwater

2.2 现有预测公式的适用性分析

选择相关性系数()、一致性指数(a)、散度指数(SI)以及偏差指数(Bias)作为度量指标进行统计学分析，来表征预测公式性能上的优劣．上述统计指数表达式分别为

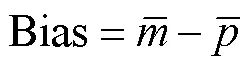
使用文献[12]和[13]中的预测公式预测透空式防波堤的波浪爬高，并与试验值做对比验证其有效性.预测值与实测值的对比如图3所示．

图3 使用已有公式预测值与实测值对比

表4为利用文献[12]和[13]的预测公式预测透空式防波堤波浪爬高结果的统计指数结果．从统计结果可以发现，现有公式对透空式防波堤的预测结果具有一定的准确性，但在波浪爬高较大时误差较大，且现有公式仅考虑了波高对直立堤爬高的影响．由于水体黏滞性等其他因素的影响，其有量纲的形式应用到实际工程中会降低预测结果的准确性．因此，本文拟采用多种预测方法针对透空式防波堤发展波浪爬高的预测公式，为实际工程中透空式防波堤的堤顶高程设计提供相应的参考．

表4 已有公式预测透空式防波堤波浪爬高统计指数

Tab.4 Statistical indicators for predicting wave run-up of permeable breakwaters by existing formulas

3 波浪爬高预测方法

3.1 多项式回归方法

多项式回归模型属于线性回归模型的一种，通过构造多项式函数来拟合各种指标的变化趋势，被广泛应用于信息学、金融学以及社会学等领域的预测中．

多项式函数是由常数及自变量经过有限次乘法与加法的混合运算得到，其基本表达式为

式中a为多项式系数．

3.2 速度水头理论

速度水头理论是估算海洋建筑物波浪爬升高度的一种较为经典的计算方法．基于Hallermeier[15]于1976年在圆柱形基础波浪爬高的研究中所提出的波浪爬高估算理论，即当在入射波传播至基础前方时，处于波峰处的水质点的动能会转化为波峰液面上2/(2)高度的势能．因此，本文中防淤积型透空式防波堤波浪爬高高度的估算公式可以表示为

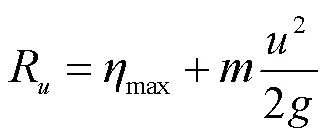
3.3 M5'模型树算法

机器学习方法通过实例数据或已有的经验规律来训练计算机，达到优化某种性能和标准的目的. M5模型树算法作为常用的机器学习算法之一，在工程领域得到了广泛的应用．它最早是由Quinlan[16]提出，并由Wang等[17]完善．M5模型树是将输入区域划分为若干个子区域，每个子空间内对应1个线性模型，通过若干分段线性模型的组合形成问题的最终解.图4为M5模型树的简单示例，其主要原理如下.

(1) 依据决策树原理构建树．根据原始数据得到初始的树状结构；将最具有识别力的属性作为子树的根节点；基于训练集中类值的标准差作为该节点误差的度量，将降低样本期望误差作为分割空间的标准，选择期望误差减少值(SDR)达到最大的属性作为分裂属性．

(2) 为解决决策树构建过程中产生复杂结构而引起的过度拟合问题，需要对决策树进行修剪．用某一节点训练集所有实例的预测值与实际值之间的绝对误差计算均值，引入补偿系数(＋)/(－)处理低估的期望误差，其中是该节点训练实例数量，是该节点预测值的线性模型所用的参数数量．通过引入补偿系数减少了属性项数，使得估计误差达到最小化，进一步简化了线性模型．

(3) 剪枝后决策树叶节点上相邻近的线性模型之间会出现突变点，使用平滑技巧修改相邻的线性方程，使得对应于不同方程的相邻输入变量的预测值更加接近．平滑公式表示为

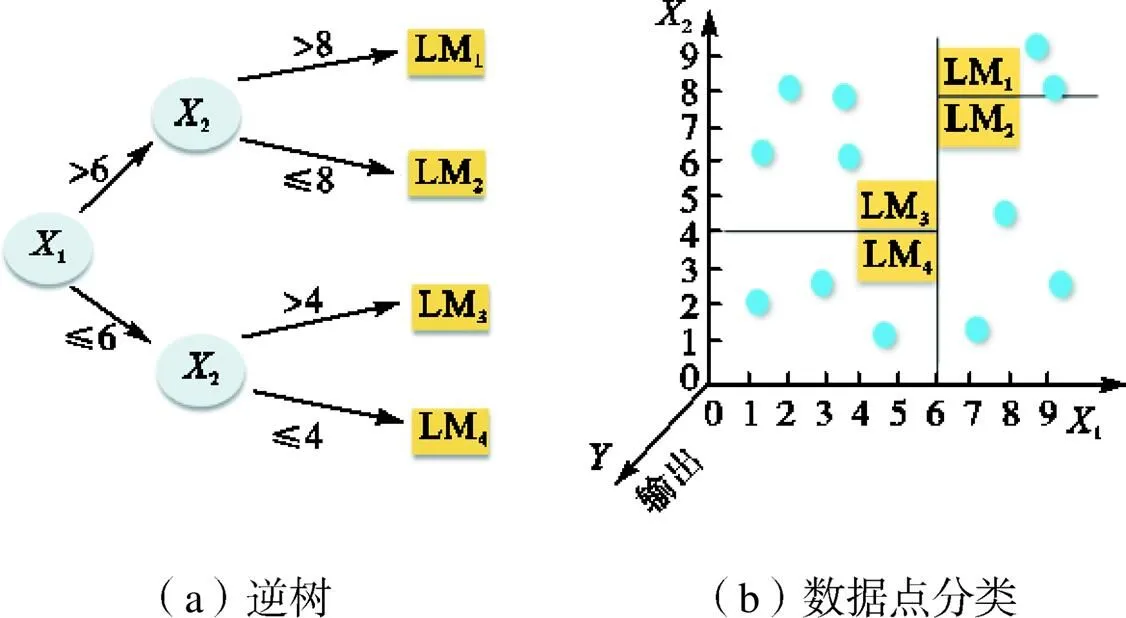
图4 M5′模型树流程

4 分析与讨论

4.1 采用多项式回归方法

图5 多项式函数拟合曲线

由多项式函数拟合曲线得到其函数关系为

多项式回归方法发展的预测公式的预测值与实测值的对比结果如图6所示．当波浪爬高值低于0.14m时，该公式的预测结果较好，数据离散程度较小．而当波浪爬高值大于0.14m时，数据的离散程度较大，该公式对波浪爬高值的预测可靠性降低．另外，该公式仅由波高参数发展而来，同一波高下波浪爬高的预测结果相同，未体现其他参数对波浪爬高的影响．

图6 多项式回归方法发展公式预测值与实测值对比

4.2 基于速度水头方法发展的新公式

在物理模型试验的基础上，运用速度水头方法，通过选取合适的波浪理论来求解速度水头方法中所需的各项波浪运动要素．通过对速度水头系数的拟合，得出透空式防波堤波浪爬高高度的预测公式．

通过计算可知，所有试验条件下的厄塞尔数值全部小于临界值15，因此本次试验工况应用微幅波理论对波浪要素进行计算．利用波高和周期计算波浪运动要素中的max和波峰处水质点最大水平速度(max)，而后拟合系数，明确海洋环境中R,max的预测公式.

计算波浪运动中的最大自由波面为

计算波面的最大水平分速度为

以静水面为原点建立波动域内的速度势函数(，，，)．式(11)中为波峰处水质点的纵坐标，为波数．

结合防波堤波浪爬高公式可以得出不同工况下的值，并与厄塞尔数U进行拟合．拟合结果如图7所示，图中曲线表示不同工况下值与厄塞尔数U的变化关系．

图7 速度水头系数与厄塞尔数拟合曲线

由对数拟合曲线结果可以得出透空式防波堤下波浪爬高的关系形式为

利用式(12)计算透空式防波堤波浪爬高结果与实测值进行对比，结果如图8所示．可以看出，随着波浪爬升高度的增加，预测值与实测值之间的离散程度逐渐变大，速度水头方法发展的预测公式的可靠性逐渐降低．对于较高的波浪爬升，该公式给出的预测结果偏于危险；而对于较低的波浪爬升，该公式预测结果则偏于保守．综合来看，基于速度水头方法结合微幅波理论对透空式防波堤波浪爬高的预测结果准确性较低．

图8 速度水头方法预测值与实测值对比

4.3 采用M5′模型树算法发展的新公式

基于M5′模型树算法的原理，为了发展预测透空式防波堤波浪爬高高度的新公式，首先要选择合适的无量纲参数作为控制参数．根据防淤积型透空式防波堤的模型试验，试验水深的不同会导致波浪剖面发生变化，进而对波浪要素(包括波高、波长周期以及水深等)产生干扰．此外，涉及到透空式防波堤参数的问题，本文引入了静水面与防波堤试验模型上、下挡板间距作为参考影响因素．另外，考虑到波浪自由表面的问题，当地的重力加速度也要考虑在内，本次试验研究中取9.8m/s2．综合考虑上述因素，本次试验中透空式波浪防波堤上波浪爬高效应具有较高影响的控制参数可表示为

为确定影响波浪爬高效应的无因次化参数与相对波浪爬高之间的皮尔森相关性，进行无因次化参数的多种组合作为输入参数，相对波浪爬高作为输出参数，对输入与输出参数进行非线性化处理以满足参数之间非线性的需要．运用M5′模型树算法发展不同参数组合下的经验公式，进一步通过统计指数对所发展的公式进行评价分析，明确不同波浪条件下的最优波浪爬高预测公式．

在M5′模型树算法程序中对模型试验所得到的数据集进行训练和测试．其中66%的数据用于训练，其余用于测试．控制参数的类型及其数量直接影响模型预测公式的准确性和实用性．直观上，包含更多控制参数(输入参数)的预测公式应更加准确、可靠．表5所示为控制参数与输出参数(R,max/)之间的皮尔森相关性计算结果．

表5 无因次参数与输出参数(R,max/)之间的皮尔森相关性

Tab.5 Pearson correlation between non-dimension pa-rameters and output parameters(Ru,max/H)

为了使得公式具有通用性，对式(9)中的参数进行无因次化处理．基于Kazeminezhad等[19]和Bonakdar等[20]在选择控制参数的研究，海洋建筑物基础上波浪爬高效应受到部分无量纲化参数的影响，具体参数如表6所示．

表6 波浪爬高预测公式的M5′模型构建

Tab.6 Construction of the M5′ model for wave run-up prediction formula

在海洋波浪环境作用下，相对波浪爬高参量(R,max/)与无量纲参数(相对水深、波陡及散射参数)之间并不是线性相关．但M5′模型树是1个多元分段的回归模型，在叶节点产生线性模型．因此，为了满足M5′模型树应用的要求，要利用非线性技巧对输入参数与输出参数进行对数化处理，以满足参数之间的非线性要求．

对所有的原始数据分类后，对每个生成的子集使用非线性技巧(对数化处理)，然后运用M5′模型树算法对表6中的MT1～MT4模型发展相应的公式．最后，利用统计指数对上述模型所发展的预测公式的性能进行表示，结果如表7所示．相较于MT1模型，其他3种模型所发展的预测公式有较好的统计误差结果，这与选取的控制参数数量有关，即更多的控制参数所发展的预测公式具有更高的准确性、可靠性.从数学角度来看，MT4模型拥有最佳的统计指数结果．另外，MT4模型包含1与2两个结构参数，能够更好地反映防波堤透空段在波浪能量垂向分布中所占的比重．因此，透空式波浪防波堤上由MT4模型发展的波浪爬高预测公式为

表7 M5′模型所发展新公式统计指数结果

Tab.7 Statistical index results for the new formula devel-oped by the M5′ model

由式(14)可以看出，相对波浪爬高参量(R,max/)值由相对波高(/)以及防波堤参数(1/)与(2/)共同决定．因此，防波堤的波浪爬高值的预测结果与波浪运动要素以及防波堤的性能参数都有关，该预测公式具有较高的准确性和可靠性．

图9为基于M5′模型树算法发展的透空式防波堤波浪爬高预测公式的计算值与物理模型试验的实测值之间的对比分布．可以看出，随着波浪爬升高度的增加，采用M5′模型树算法发展的预测公式得出的预测值与试验实测值的离散程度随波浪爬高逐渐增大，准确性降低．但预测值与实测值总体上具有较高的一致性，离散程度较小，因此基于M5′模型树算法发展的预测公式具有较高的可靠性．

图9 M5′模型树算法预测值与实测值对比

5 结 论

以防淤积型透空式防波堤为研究对象，采用物理模型试验的方法探究了不同工况下波浪爬高特征.分别采用多项式回归方法、速度水头方法以及M5′模型树算法提出了透空式防波堤波浪爬高预测方法，得到如下结论．

(1) 采用多项式回归方法拟合的预测公式能够较好地预测防波堤的波浪爬高，但该公式仅由波高参数发展而来，忽略了其他波浪条件以及结构物参数对波浪爬升高度的影响，在实际工程应用中具有较大的局限性．

(2) 速度水头方法结合波浪运动理论发展的预测公式拥有可靠的理论依据，但预测结果表明该方法对波浪爬高结果的预测与试验值偏差较大，统计指数所反映的公式性能也较差，难以准确预测透空式防波堤的波浪爬高．

(3) M5′模型树算法发展的波浪爬高预测公式综合考虑了各项波浪要素以及防波堤的结构参数等，具有良好的统计指数，能够更好地预测透空式防波堤的波浪爬高．相比其他两种方法发展的预测公式，M5′模型树算法采取参数无量纲化的方式拓宽了该公式的适用范围，提高了其在实际工程中的应用价值．

［1］ Vahidi M，Pirooz M D，Nikoo M R，et al. Optimization of double-layer perforated breakwater based on risk assessment of uncertainties[J]. Ocean Engineering，2022，265：112612.

［2］ Elsheikh A K，Mostafa Y E，Mohamed M M. A comparative study between some different types of permeable breakwaters according to wave energy dissipation[J]. Ain Shams Engineering Journal，2022，13(4)：101646.

［3］ Li Y T，Wang D T，Sun T T，et al. Fully coupled simulation of interactions among waves，permeable breakwaters and seabeds based on N-S equations[J]. China Ocean Engineering，2021，35(1)：26-35.

［4］ Koraim A S，Heikal E M，Rageh O S. Hydrodynamic characteristics of double permeable breakwater under regular waves[J]. Marine Structures，2011，24(4)：503-527.

［5］ Yu T，Li Y，Chen X，et al. Experimental study on wave- and current-induced scour around an anti-deposition permeable breakwater[J]. Ocean Engineer-ing，2022，257：111565.

［6］ 李春潮，曾南海，刘东征. 科伦坡港口城外防波堤堤顶高程的确定[J]. 水运工程，2015(9)：94-98.

Li Chunchao，Zeng Nanhai，Liu Dongzheng. Determination of top elevation Colombo port city off-breakwater[J]. Port & Waterway Engineering，2015(9)：94-98(in Chinese).

［7］ 郑丽娜. 论“设计波浪入射角度对防波堤顶高程取值的影响”[J]. 中国水运，2018，18(5)：151-152.

Zheng Lina. On “The influence of design wave incident angle on the crest elevation of breakwater”[J]. China Water Transport，2018，18(5)：151-152(in Chinese).

［8］ Diwedar A I. Investigating the effect of wave parameters on wave runup[J]. Alexandria Engineering Journal，2016，55(1)：627-633.

［9］ Guo Xiaoyu，Wang Benlong，Liu Hua. Numerical simulation of irregular wave overtopping against a smooth sea dike[J]. China Ocean Engineering，2012，26(1)：153-166.

［10］ 朱嘉玲，王 震，孙天霆，等. 斜向规则波作用下斜坡堤波浪爬高试验研究[J]. 中国港湾建设，2017，37(2)：33-37.

Zhu Jialing，Wang Zhen，Sun Tianting，et al. Experimental study on wave run-up of sloping seawall under oblique regular waves[J]. China Harbour Engineering，2017，37(2)：33-37(in Chinese).

［11］ Bonakdar L，Etemad-Shahidi A. Predicting wave run-up on rubble-mound structures using M5 model tree[J]. Ocean Engineering，2011，38(1)：111-118.

［12］ 朱昭力，柯维林，陈国平，等. 不规则波作用下带挑檐直立堤爬高与越浪量试验[J]. 水运工程，2019(4)：21-24.

Zhu Zhaoli，Ke Weilin，Chen Guoping，et al. Experiment of wave run-up and overtopping of vertical breakwaters with wave return wall under irregular waves[J]. Port & Waterway Engineering，2019(4)：21-24(in Chinese).

［13］ 刘 堃，陈哲淮，唐 云，等. 低桩承台直立结构波浪爬高与越浪量[J]. 水运工程，2018(9)：38-41.

Liu Kun，Chen Zhehuai，Tang Yun，et al. Wave run-up and overtopping discharge on low pile platform vertical sea dike[J]. Port & Waterway Engineering，2018(9)：38-41(in Chinese).

［14］ 中华人民共和国交通运输部. JTS 154-1—2011 防波堤设计与施工规范[S]. 北京：人民交通出版社，2011.

Ministry of Transport of the People’s Republic of China. JTS 154-1—2011 Code of Design and Construction of Breakwaters[S]. Beijing：People’s Transportation Pub-lishing House，2011(in Chinese).

［15］ Hallermeier R J. Nonlinear flow of wave crests past a thin pile[J]. Journal of the Waterways，Harbors and Coastal Engineering Division，1976，102(4)：365-377.

［16］ Quinlan J R. Learning with continuous classes[C]//5th Australian Joint Conference on Artificial Intelligence. Singapore：World Scientific，1992.

［17］ Wang Y，Witten I H. Induction of model trees for predicting continuous classes[R]. New Zealand：The University of Waikato，1996.

［18］ Skovgaard O，Jvendsen I A，Jonsson I G. Sinusoidal and Cnoidal Gravity Waves Formulae and Tables[M]. Lyngby：Institue of Hydrodynamics and Hydraulic Engineering，Technical University of Denmark，1974.

［19］ Kazeminezhad M H，Etemad-Shahidi A. A new method for the prediction of wave runup on vertical piles[J]. Coastal Engineering，2015，98：55-64.

［20］ Bonakdar L，Oumeraci H，Etemad-Shahidi A. Run-up on vertical piles due to regular waves：Small-scale model tests and prediction formulae[J]. Coastal Engineering，2016，118：1-11.

Experimental and Prediction Study on Wave Run-Up of Anti-Deposited Permeable Breakwater

Yu Tongshun1，Zhao Xuewen1，Tang Junhui2，Zhang Zhenyu1，Chen Xingyu1

(1. College of Engineering，Ocean University of China，Qingdao 266100，China；2. Northeast Electric Power Design Institute Co.，Ltd.，China Electric Power Engineering Consulting Group，Changchun 130000，China)

Wave run-up is an important factor influencing the elevation design and project cost estimation of breakwater. In this paper, an anti-deposited permeable breakwater was taken as the research object, the physical model run-up experiment of the breakwater was carried out under 64 different working conditions with a model scale of 1∶10, and the maximum wave run-up height on the wave side of the breakwater under different working conditions was recorded, thereby exploring the wave run-up characteristics of the breakwater. The prediction formulas for the wave run-up of the permeable breakwater were developed using the polynomial regression method, velocity stagnation head method and M5model tree algorithm respectively combined with the results of the physical model experiment, which were further compared and analyzed by means of statistical parameters. First, results show that the wave surface change on the back side of the permeable breakwater lags behind that on the wave side, and the maximum wave run-up on the back side is less than that on the wave side, indicating that the breakwater has a satisfying wave dissipation effect. Second, the prediction formulas developed by the polynomial regression method and velocity stagnation head method respectively can predict the wave run-up of breakwater to a certain extent. The former only considers the wave height but ignores the influences of other wave conditions and the breakwater’s structural parameters on the wave run-up height, while the latter has a large deviation between the prediction results and experimental values of wave run-up, indicating that both have certain limitations in practical applications. Third, the wave run-up prediction formula developed by the M5model tree algorithm uses non-dimension parameters to integrate various wave parameters and the breakwater’s structural parameters, so it has good statistical indexes and can better predict the wave run-up of the permeable breakwater, which is of high practical application value.

permeable breakwater；wave run-up；physical model experiment；polynomial regression method；velocity stagnation head；M5model tree；statistical parameter；prediction formula

10.11784/tdxbz202211028

P753

A

0493-2137(2023)08-0831-09

2022-11-17；

2023-02-21.

于通顺（1986—  ），男，博士，教授.Email：m_bigm@tju.edu.cn

于通顺，tshyu707@ouc.edu.cn.

国家自然科学基金资助项目(51739010)；山东省泰山学者计划资助项目(ts20190914).

the National Natural Science Foundation of China(No.51739010)，the Taishan Scholars Program of Shandong Province (No.ts20190914).

(责任编辑：武立有)