基于循环对抗神经网络的快速最小二乘逆时偏移成像方法

2023-06-19黄韵博黄建平李振春刘博文

中国石油大学学报（自然科学版） 2023年3期

黄韵博, 黄建平, 李振春, 刘博文

(中国石油大学(华东)地球科学与技术学院,山东青岛 266580)

地震偏移成像的目标是通过地震数据对地下构造对应的反射系数模型进行精确成像[1]。提高成像的分辨率对于非常规油气勘探及小尺度地质目标的刻画十分重要。但是,常规的偏移算子只是正演算子的转置,而不是它的逆,无法完全逆转地震波传播效应[2],因此常规偏移方法存在分辨率低、照明不均、偏移假象以及低频噪音严重等问题[3-4]。为了得到更加精确的成像结果,可以将成像问题放入最小二乘反演框架,利用迭代最小二乘法求解,即最小二乘偏移[5-8]。近年来,最小二乘偏移已被证明能够提高不完整数据[9]成像质量和均衡不均匀地震波照明。最小二乘偏移包括模型域最小二乘偏移[10-12]和数据域最小二乘偏移[13-20]。模型域的最小二乘偏移是通过少量的迭代计算出Hessian矩阵的逆矩阵,将其直接作用于常规偏移结果,得到高精度成像结果。但是,Hessian矩阵十分庞大,对存储量要求极高[21]。数据域的最小二乘偏移则是通过迭代最小二乘法,逐步更新反射系数模型,这种方式不需要存储Hessian矩阵,但是需要大量迭代计算量。近年来,深度学习被广泛应用于地球物理领域以解决断层识别[22]、地震数据去噪[23]以及初至拾取[24]等问题,并取得了良好的效果。笔者采用循环对抗神经网络[25]来近似替代Hessian矩阵的逆矩阵,将训练后的网络直接作用于逆时偏移[26-27]的结果,快速提高成像质量。选取3个速度模型,通过有限差分正演和逆时偏移成像得到训练数据中的输入数据,通过雷克子波与反射系数褶积得到训练集中的输出数据。同时,再选取另外两个模型作为验证集,测试网络训练后的预测效果,验证集不参与模型训练。

1 方法原理

1.1 偏移理论

对于给定的反射系数m和线性正演算子L,观测数据d可以表示为

d=Lm.

(1)

地震成像的目标是寻找准确的m来拟合观测数据d,常规逆时偏移成像可以表示为

mmig=LTd.

(2)

式中,mmig为逆时偏移成像结果的矩阵表示;LT为逆时偏移算子的矩阵表示。LT只是正演算子的转置,并不是它的逆,故逆时偏移的成像结果并不能精确表示真实反射系数模型。

对真实反射系数m的求解可以放在最小二乘框架下进行,本文中定义最小二范数的目标泛函f(m)为

(3)

由此可以得到反射系数m的最小二乘解为

m=(LTL)-1LTd.

(4)

这里(LTL)-1即Hessian矩阵的逆矩阵,式中LTd为逆时偏移的结果,因此逆时偏移成像结果和真实反射系数模型之间的关系可以表示为

m=H-1mmig.

(5)

常规二维声波方程表达式为

(6)

式中,σ(x)=1/ν(x)为介质的慢度场;ν(x)为对应的介质速度场;fs(ω)为震源项,表示脉冲震源点在xs处,圆频率为ω。基于反演问题近似线性的假设,对于这个二维声波方程,其Hessian矩阵的表达式可以写成如下形式:

GT(xs,y,ω)×G(x,xr,ω)GT(y,xr,ω)}dω.

(7)

式中,G(xs,x,ω)为激发点的格林函数;G(x,xr,ω)为接收点xr的格林函数;fs(ω)为震源子波在频率域的表示。格林函数项反映了成像过程中地震波的照明问题,而震源子波项则对成像分辨率产生影响。

结合式(5)和式(7)分析可得,逆时偏移结果受到Hessian矩阵的影响,表现出成像分辨率低、照明不均及偏移噪音等问题。求解得到Hessian矩阵的逆矩阵,将其作用于逆时偏移的成像结果,便可以得到真实的反射系数模型,这种方式即模型域最小二乘逆时偏移。但是,直接求解Hessian矩阵的逆需要很大的计算量和存储量,对于实际应用来说适用性不好。另一种方式是数据域最小二乘逆时偏移,即通过迭代算法不断更新反射系数,使得模拟出来的数据和观测数据之间的误差达到最小或期望值。数据域最小二乘逆时偏移同样需要大量的计算成本。本文思想与模型域最小二乘逆时偏移类似,采用循环对抗神经网络来近似表征Hessian矩阵的逆矩阵,将训练后的网络直接作用于逆时偏移的成像结果,得到高质量的成像剖面。

1.2 循环对抗神经网络

对抗神经网络(GAN)在源域向目标域的转换问题上有良好的适用性,常被用于风格迁移。常规的神经网络是通过反传算法寻找一个输入到输出的最佳映射关系,网络的本质可以看作一个复杂的高阶多项式。对抗神经网络一般有两部分网络组成,一部分作为生成器,另一部分作为鉴别器。在网络的训练过程中,生成器充当常规神经网络的角色,将输入转换为和输出类似的数据,而鉴别器会以生成器的输出数据作为输入,尝试区分哪些是生成的数据,哪些是训练集里的真实数据。通过这种对抗式的训练,生成器和鉴别器都在不断优化,最终得到期望效果的生成器作为预测网络。

循环对抗神经网络由2个镜像对称的对抗神经网络组成,共同构成一个环形网络。如图1所示,cycleGAN有2个生成器和2个鉴别器。对于源域数据X,由红色虚线代表的单向GAN生成Y1和X1,Y1进入鉴别器鉴别真伪。反过来,作为目标域的数据Y也可以作为输入,由绿色虚线代表的另一个单向GAN生成X2和Y2,X2进入鉴别器做真伪鉴别。生成器由编码器、转换器和解码器构成,编码-解码结构与大多数卷积神经网络类似,用卷积层和反卷积层来实现特征提取和还原,转换器的结构由多层Resnet来实现。鉴别器由基本的卷积神经网络来实现,其判别图像需要从输入图像上提取特征,最后添加一维输出的卷积层来确定所提取的特征是否属于特定类别。

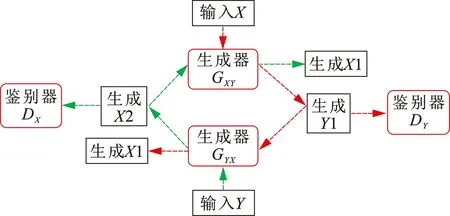
图1 循环对抗神经网络结构Fig.1 Structure of cycle-consistent adversarial neural network

1.3 损失函数

损失函数是衡量网络输出结果好坏的标尺,同时也是反传过程中修正张量梯度的依据。对于一个给定大小的训练批次,假设源域的数据分布为px,目标域的数据分布为py,则每一个训练数据x和y的数据分布可以表示为x～px和y～py。因此常规GAN的目标函数可以表示为

LGAN(GXY,DY,X,Y)=Ey～py[logDY(y)]+Ex～px[log(1-DY(G(x)))].

(8)

在训练过程中,生成器GXY试图生成更像反射系数的GXY(x),而鉴别器DY则试图区分开生成的GXY(x)和目标域中真实的反射系数y。因此,生成器的目标是使目标函数最小化,而鉴别器的目标是使目标函数最大化。对于第一个GAN,其最终目标是minGmaxDYLGAN(GXY,DY,X,Y),同样地,对于另一个GAN,其目标为minGmaxDYLGAN(GXY,DX,Y,X)。

由上述目标函数的约束,理论上GAN可以将任意的源域映射至目标域。但是,只有这个约束可能导致生成器只是生成一个具有反射系数特点的结果,而结构内容与源域数据并不一样,即通过训练只实现了风格的迁移,并没有保证内容不发生变化。对于任意一个源域数据x,需要保证x→GXY(x)→GYX(GXY(x))≈x,这也称为前向循环一致性。同样地,对于任意一个目标域数据y,也需要其满足反向循环一致性,即:y→GYX(y)→GXY(GYX(y))≈y。因此cycleGAN引入了循环一致性误差函数如下:

(9)

通过上述误差函数的约束,对于源域或者目标域的任一数据,经过两个生成器的循环,最后可以有效还原至原始数据特征。但是,当训练完网络进行应用时,风格完成迁移但内容发生改变的情况还是会发生。通过分析可知,应用时只采用了一个生成器作为预测网络,而循环一致性误差函数没有对中间变量进行约束。因此,本文中引入身份误差函数对中间变量进行约束,其表达式为

(10)

因此对cycleGAN进行训练时,其整体误差函数如下所示:

L(GXY,GXY,DX,DY)=LGAN(GXY,DY,X,Y)+LGAN(GYX,DX,Y,X)+Lcycle(GXY,GYX)+Lidentity(GXY,GYX).

(11)

1.4 训练集制作

如图2所示,本文中选取了BP2.5D模型、SEAM模型以及Pluto模型作为基础模型来制作训练数据。通过有限差分正演和逆时偏移得到三个模型对应的成像结果。同时,基于速度模型生成了反射系数模型。考虑到反射系数模型与偏移成像结果的频带范围差异性较大,采用褶积的方式,用雷克子波对反射系数模型做褶积,作为目标域数据。最后采用裁切、重采样等数据增强方式得到了300对训练数据。部分训练数据如图3所示,第一排为源域的逆时偏移成像数据,第二排为目标域的褶积结果。

图2 用于生成训练集的速度模型和对应的逆时偏移成像结果Fig.2 Velocity model used to generate training set and corresponding reverse time migration imaging results

图3 部分用于训练的输入输出数据Fig.3 Some input and output data used for training

1.5 训练

循环对抗神经网络的训练流程如图4所示,对于源域至目标域的单向GAN,训练时先固定生成器GXY,单独训练鉴别器DY,提升鉴别器对生成器输出结果的鉴别能力,然后再固定鉴别器DY,单独训练生成器GXY,使其生成更具有目标域风格的结果,绕开鉴别器的识别。通过这种对抗式的训练方式,能够极大提升生成器GXY向目标域映射的能力。同理,对于另一个目标域反映射至源域的单向GAN,也采用同样的对抗式训练。当两个GAN训练一轮后,将所有损失函数的值累加,判别其是否满足期望的误差大小,若大于期望误差,则进入下一轮训练,相反,若小于期望误差,则结束训练。最后,将生成器GXY作为期望的预测网络,用于近似替代Hessian矩阵的逆,对新的逆时偏移成像结果进行预测处理,输出高质量的成像结果。

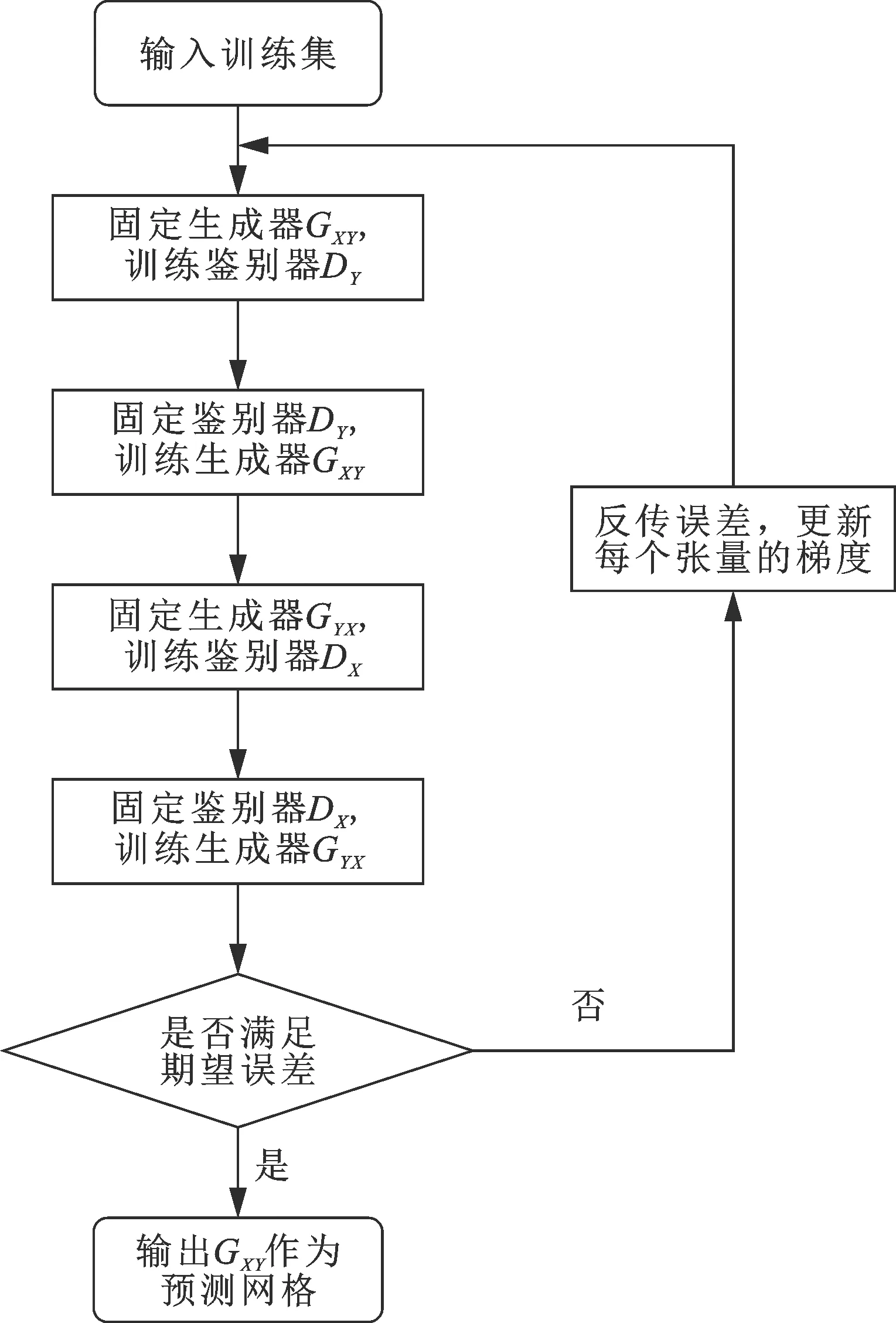
图4 循环对抗神经网络训练流程Fig.4 Training process of cycle-consistent adversarial neural network

网络训练的迭代次数设置为200次,学习率为0.0002,在进行到第100次迭代后,学习率逐步下降。网络的循环一致性误差权重为10,身份误差的权重设置为5。基于pytorch平台,使用单个NVIDIA RTX5000 GPU训练,训练总耗时10 h。

2 模型试算

2.1 Marmousi模型预测

图5(a)为Marmousi速度模型,对其进行有限差分正演和逆时偏移后,得到的偏移成像结果如图5(c)所示。由于受到Hessian矩阵的影响,RTM成像结果在浅层有较多的低频噪音。同时,受模型深部高速屏蔽层的影响,模型底部构造成像分辨率低。图5(d)是网络预测的结果,对比图5(c)可得,预测出的成像结果整体分辨率有了较大提升,反射层位更加精细。浅层的低频噪音大大减弱,在两侧有少量残留,训练好的网络所得成像结果中的炮点痕迹不可见。深层的成像质量也得到了提升,但是也有一些错误成像出现,这是因为RTM的成像结果中存在一些杂乱的成像能量,被网络误认为层位并恢复出来。

图5 Marmousi模型预测结果Fig.5 Prediction results of Marmousi model

2.2 Sigsbee2A模型预测

图6是Sigsbee2A模型的预测结果对比。图6(a)是速度模型,模型中有横向展布较大的高速盐丘。同样的,对其进行有限差分正演和逆时偏移后,得到图6(c)所示的逆时偏移成像结果。Sigsbee2A模型的成像剖面同样存在着明显的低频噪音和炮点痕迹,在速度差异较大的分界面附近以及盐丘内部存在着一些偏移假象和噪音,同时,由于盐丘对地震波的屏蔽作用,盐下成像能量十分微弱。图6(d)是网络对图6(c)的预测结果,对比图6(c)可以看出,预测结果的成像分辨率得到了提升,成像能量照明均匀,浅层没有低频噪音影响和炮点痕迹消失,盐下成像质量提升明显,盐丘边缘和内部的偏移假象也得到了压制。在成像质量提升的同时,预测结果中的绕射点成像效果变差,这可能是因为训练集的数据不包含绕射点的成像数据,网络未能学习到与绕射点相关的特征。针对此问题,后期可以在数据集中加入具有绕射点相关特征的数据,提升网络的泛化能力。