新课程理念下基于HPM视角的计算教学实践与思考
2023-06-19郝勤秀
郝勤秀


【摘 要】体现课程内容的一致性、整体性是《义务教育数学课程标准(2022年版)》的基本要求。新课标在课程理念部分明确提出要“关注数学学科发展前沿与数学文化,继承和弘扬中华优秀传统文化”。新课程理念下基于HPM视角的计算教学,注重让算理具有丰富的意义,让学生真正经历算法的形成过程,实现“再创造”,让数学文化充满课堂。
【关键词】新课标 HPM视角 计算教学 实践与思考
计算是所有数学活动的基础,计算教学在小学数学教学中有着举足轻重的地位。多年来,许多教师对计算教学的探索形成了许多宝贵的经验:让学生更好地在理解算理的基础上掌握算法(来源于教材),从而能正确计算并灵活运用。事实上,如果坚持“唯教材”论,那么学生对算理的理解、算法的掌握,可能会浮于表面,导致学生的知识不成系统,这有违新课标“体现课程内容的一致性、整体性”这一基本要求。基于此,本文拟从HPM(数学史与数学教育)角度研究计算教学。
一、问题的提出——为什么一定要“从高位算起”
学校一位青年教师执教“两、三位数除以一位数”这节课后,学生问她一个问题:“列竖式计算除法时,为什么一定要从高位算起?你看我从低位算起也可以(如图1)。”这位青年教师当时被问蒙了,简单回答道:“除法竖式计算一般都从高位算起。”
针对这个问题,笔者在一定范围内做了调查,绝大部分学生没有想过这个问题,觉得书上就是这样的。几乎所有的教师在课上也没有引导学生思考过这个问题,一般都是结合问题情境引导学生理解算理,然后很顺当地形成算法。为什么从高位算起呢?教师们大致有这几种想法:一是认为除法从高位算起,简便;二是结合分物品的现实经验出发,先分多的,再分少的;三是认为这是除法竖式计算的法则。学校的这位青年教师就是第三种想法。这引起了笔者的思考,我们究竟应该怎样进行计算教学?
每一种运算法则的形成都有其历史过程,只有了解人类是如何发明计算方法的,才能对如何让学生真正“理解算理、掌握算法”做出更好的判断。数学史和数学教学的结合已是国际数学课程改革的趋势,HPM视域下的计算教学是《义务教育数学课程标准(2022年版)》理念下的新样态。
二、教改措施——HPM视域下的计算教学
“两、三位数除以一位数”这个内容很重要,它是后续学习“除数是两位数的笔算除法”的基础。以苏教版数学为例,教学时,教师一般会利用教材提供的情境进行教学;通过学习让学生理解算理、掌握算法:从高位算起,一位位地算,哪一位上不够商1要商0……看似是非常完整、有深度的教学,实际上没有真正揭示计算方法的本质。
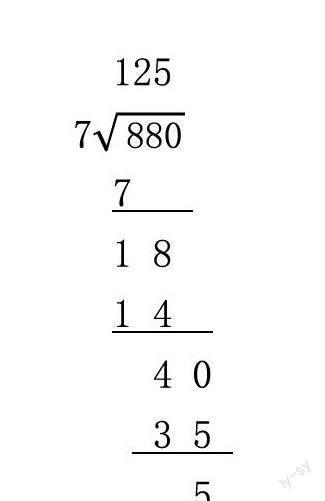
加减法和乘法都是从低位开始算起的,为什么列竖式笔算除法时要从高位算起呢?克莱因指出,历史是教学的指南。追本溯源,与现在比较接近的是出现于公元980年的Gerbert方法。以“880÷7”为例,现在是这样写的:
Gerbert方法是这样的,除数7写成“10 3”,商写在被除数的右边:
该过程的第一步,880除以10商88,但实际除以7,显然多“分掉”264(3×88=264),实际剩下264需要继续分,第二步商26,“分掉”260,剩下4,再加上這里多“分掉”的78(3×26=78),实际剩下82……像这样一直分下去,最后把每次的“过程商”加起来就是最后的商。
Gerbert方法经过历史演变,变成下面的除法竖式(如图2)。变化后的过程将标准算法中隐藏的位值原理凸显出来,表面上看起来复杂,实则更直观也更易理解。
竖式的演变过程证明了一点:除法竖式是为了计算简便,这为我们探究“笔算除法为什么从高位算起”提供了思路。
从除法模型角度分析:除法计算是平均分的数学模型。比如48÷3,可以理解为把48根小棒平均分成3份,每份是多少根?平均分的时候可以先分“捆”,每10根小棒1捆,还剩下1捆和8根小棒合起来再平均分,每份6根,最后结果为每份1捆带6根,也就是16根;也可以先分“根”,每份2根,剩下2根不够分,接着分4捆,每份1捆,最后把剩下的1捆和2根合起来再平均分,每份4根,所以最终结果是2+10+4=16(根)。通过上述分小棒的过程,我们发现,从“根”开始分比从“捆”开始分的过程更复杂。结合实际,在平均分的时候,人们更愿意从大单位开始分,这与列竖式计算除法时从高位算起相对应。
从计算过程来看:除法竖式的计算和其他运算一样,也是一位一位地算,如果被除数每一位上的数都正好被除数整除,那么从高位算起与从低位算起几乎无差别。实际上,一般情况下各数位上的数平均分后会出现“盈”“亏”情况,在这种情况下,从高位算起就占优势。比如:计算41÷2,从个位算起,个位上的1除以2不够除,要从十位“借一当十”,再和个位上的1合起来除以2,11÷2=5……1,接着十位上剩余的3和个位上的余数1合起来是31再除以2,这时又遇到个位上的1不够除的情况,需要再从十位上“借一当十”……一直这样操作下去,最后还要把若干次“过程商”加起来。被除数越大,从低位算起时需要向较高位“借一当十”的步骤越多,过程越烦琐。
从除法竖式的书写形式来看:在二年级第一次接触“有余数的除法”时,除法竖式完整记录了每一步的计算过程。为了保证知识的系统性和连续性,在“两、三位数除以一位数”的竖式计算中,也要从高位算起,这样才能和“有余数的除法”一样,完整展现每一步的思考与计算过程。如果从低位算起,计算过程中有时会因为不够除而要向较高位“借一当十”,而且余数也经常会出来“调皮捣蛋”,过程显得“混乱”,一道竖式无法展示思维的全过程。
通过以上分析可知,除法竖式计算从低位算起也可以,只是从高位算起更合理。对比加减法和乘法,它们本质一样。加、减法和乘法在列竖式计算时从高位算起也是可以的,只是遇到进位或退位时不方便罢了。所以,四则运算中不管哪种运算,强调从低位算起和高位算起的本质都是相同的,都是为凸显计算程序的优化、简便。
结合本文开始那个学生产生的疑问及以上分析,笔者在设计“两、三位数除以一位数”的教学时,把除法竖式的“历史”作为知识背景,整合教材内容,将教材例题3和4放在一节课中尝试教学,力求让学生经历“再创造”除法竖式的历程。
层次一:出示例题情境图让学生读懂题目,尝试列式并组内交流。分小棒,可以先分“捆”,再分“根”;也可以先分“根”,再分“捆”。
40÷2=20 6÷2=3
6÷2=3 40÷2=20
20+3=23 3+20=23
设计意图:分的过程可以从两个不同的角度去思考,为之后尝试列竖式笔算除法提供思维方向。
层次二:尝试列竖式计算46÷2,讨论到底从高位算起,还是从低位算起。
设计意图:除法竖式书写过程和“现实分”的过程是一致的。教师引导学生初步体会从高位算起和从低位算起都可以。
层次三:改编例题,将46个羽毛球改成36个。现在你还能尝试列竖式计算吗?学生独立计算,交流体会。
设计意图:让学生充分讨论,体会“从高位算起和从低位算起都行,但从高位算起更简便”。
层次四:综合运用(略)。
三、实践效果及反思
心理学研究表明,计算教学要借助充分的感性材料,让学生通过操作感知并形成相关活动经验,在此基础上建立起清晰的表象,再抽象、概括出计算方法,并通过概括实现具体化,即进一步理解、巩固具体问题的解决。笔者认为HPM视域下计算教学的样态应该如下:
(一)让计算教学具有生命力
有意义的计算教学才有生命力。有意义的计算教学需具备两点:一是对于计算本身而言的,在计算教学中,算理必须厘清;一是计算教学必须揭示算法最本质、最原始的内涵。计算方法在经过动态演化形成静态的结构后,从某种程度上来说掩盖了其深层次、最本质的东西。除法算式虽是程序性规则的教学,忌直接告知,要让学生看看数学规律背后的故事,学生一定有这样的期待。
(二)让学生真正经历过程
让学生真正经历过程,这里的过程,一是指已经形成的知识结构过程,二是指知識的历史形成过程。让学生充分感受、重演数学知识的历史,尽管他们的发现可能是零碎的、初步的,甚至是错误的,但恰恰是这样的过程让学生与数学家感同身受,让学生感受到数学知识的趣味和内在美。同时,为了让学生能真正经历过程,教师要为他们创设良好的探究环境,激发学生探求数学真知的兴趣和动力。另外,教师要为学生“经历计算”创造良好的、适切的条件,从而帮助学生建立起现实知识与历史文化之间的联系。
(三)让计算教学充满文化味
纯粹为了训练计算技能而学习,通过不停地机械训练,学生算得“又对又快”,计算能力也能逐渐提高,但他们对数学知识的学习热情会逐渐降低,甚至产生厌恶感。所以,让计算教学充满文化味显得尤为重要,教师要让学生在学习计算的过程中通过不断探索、相互交流来理解和感悟其历史文化的积淀。
或许,学生在这样的环境中学习,计算速度不及普通课堂,从表面来看效率甚至会降低,但事实上,我们进行数学教学的目的不仅仅是让学生拥有知识层面的东西,更重要的是培养学生“具有能够适应终身发展和社会发展需要的必备品格和关键能力”从这个意义上讲,HPM视域下的教学方式是最有效、最长效、最智慧的,符合新课标的基本要求,体现了新课标的课程理念
【参考文献】
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022 .
[2]刘超,代瑞香,陆书环,等.数学史与数学教育[M].杭州:浙江大学出版社,2013.
[3]郑玮,郑毓信.HPM与数学教学中的“再创造”[J].数学教育学报,2013(3).
[4]赵伟,李小强.除法缘何要从高位算起[J].小学教学(数学版),2017(12).
[5]高敏.规范,都曾经不规范——浅谈小学数学教学中的竖式计算教学[J].中小学数学(小学版),2016(6).
