数形结合巧解题

黄烨华

通过观察图形来探究数量关系，或利用数量关系来描述图形特征，从而使复杂的问题简单化，这种思想方法称为数形结合思想.用数形结合的思想解题可分为两类：①利用几何图形的直观性表示数的问题，它常常借用数轴、直角坐标系、函数图象等；②运用数量关系来研究几何图形问题，常常要建立方程（组）或建立函数关系等.下面简单介绍“数形结合”巧解初中数学题的几种情形.

一、数形结合巧解图形变化规律问题

初中阶段的图形变化规律题中往往涉及数字的变化，图形关系在发生规律性的变化时，数量关系也会随之出现规律性的变化.解题时我们应从分析图形结构的形成过程入手，从简单到复杂进行归纳猜想，从而获得隐含的数字规律，并用代数式描述出来，进而解答相关问题.

例1 图1是小明用火柴搭的1条、2条、3条“金鱼”……，则搭 n 条“金鱼”需要火柴_________根.

分析：本题虽然是图形问题，但依然可以采用数形结合思想来解.可以将火柴棒摆成的金鱼“形”转化为火柴棒的“数”量.

解：1条金鱼，有8根火柴；

2 条金鱼，有 14 根火柴，比 1 条金鱼多 6根；

3 条金鱼，有 20 根火柴，比 2 条金鱼多 6根，比1条金鱼多2×6根；

……n 条金鱼，有（）根火柴，比（n-1）条金鱼多 6 根，比（n-2）条金鱼多 2×6 根，……，比1条金鱼多（n-1）×6根；

这样，利用递推的方法就可以推算出第n条金鱼需要8+6×（n-1）=6n+2根.

点评：本题主要考查图形的变化规律.解答此类题目的方法是：从变化的图形中发现不变的部分和变化的部分及变化部分的特点.

二、数形结合巧解二元一次方程组问题

二元一次方程组和一次函数的结合很好地诠释了“数”与“形”的结合，我们可以利用两直线的交点坐标确定方程组的解，也可以利用方程组的解确定两直线的交点坐标.在利用一次函数图象解二元一次方程组时，两函数图象的交点的横坐标是 x 的值，纵坐标是y的值，正确找出交点坐标是解题的关键．

例2 用图象法解某二元一次方程组时，在同一直角坐标系中作出相应的两个一次函数的图象（如图 2 所示），则所解的二元一次方程组是（

）分析：题目已经给出方程组的图象，我们根据图象可以明确两条直线的斜率，进而直接将图象中两直线的交点坐标P带入方程即可以验证准确与否.

解：由图可知，两直线都过P（1，1）点，其中一条直线斜率为 k=-1，另一条直线斜率为k=2.对比选项，只有选项 D 满足条件，其中直线 x + y - 2 = 0的斜率为k=-1，直线2x - y - 1 = 0的斜率为 k=2，而且都满足过 P（1，1）.答案为D项.

评注：通过图象求解二元一次方程组问题，除了关注交点坐标外，还要看图象能提供哪些其他信息，同时要关注选项，对比出选项的异同点.

三、数形结合巧解二次函数问题二次函数蕴含了丰富的数形结合思想，在平面直角坐标系中，二次函数图象的开口方向、顶点坐标、对称轴以及与坐标轴的交点等都与其系数 a，b，c 密不可分.因此，在解答二次函数问题时，要把图形的性质特征与数量关系相互转化，通过观察图象分析图形与数量之间的关系，通过分析数量关系的变化判断函数图象的运动轨迹，从而求解.

例 3 图 3 为二次函数 y=ax2+bx+c 的图象，在下列说法中：①ac＜0；②方程ax2+bx+c=0 的根是 x1=-1，x2=3；③a+b+c＞0；④当 x＞1时，y随x的增大而增大；⑤2a-b=0；⑥b2=4ac＞0.结论一定成立的是（ ）.

分析：此题考查了二次函数的图象.我们可以借助于二次函数的图象和性质特征完成解题.

评注：“数形结合”要牢牢地抓住“数”的性质和“形”的特征，本题考查了同学们对二次函数的图象与系数的关系的理解和运用，同时也考查了观察图象的能力.同学们一定要重视对定义、概念以及原理的学习，这些都是数形结合的根源.

四、数形结合巧解统计问题

解答统计问题的重点在于收集数据、分析数据、将数据用图形的方式表达出来，这充分显示了数形结合思想方法的灵活运用.条形统计图、扇形统计图和折线统计图是初中数学统计学中的重点.如果是关于比重的问题，可以使用扇形统计图.如果是关于数据集中分析的问题，可以使用条形统计图.如果是关于数据变化规律问题，可以使用折线统计图.利用統计图简洁明了的特点展示数据，可以让我们对结果或者规律一目了然.

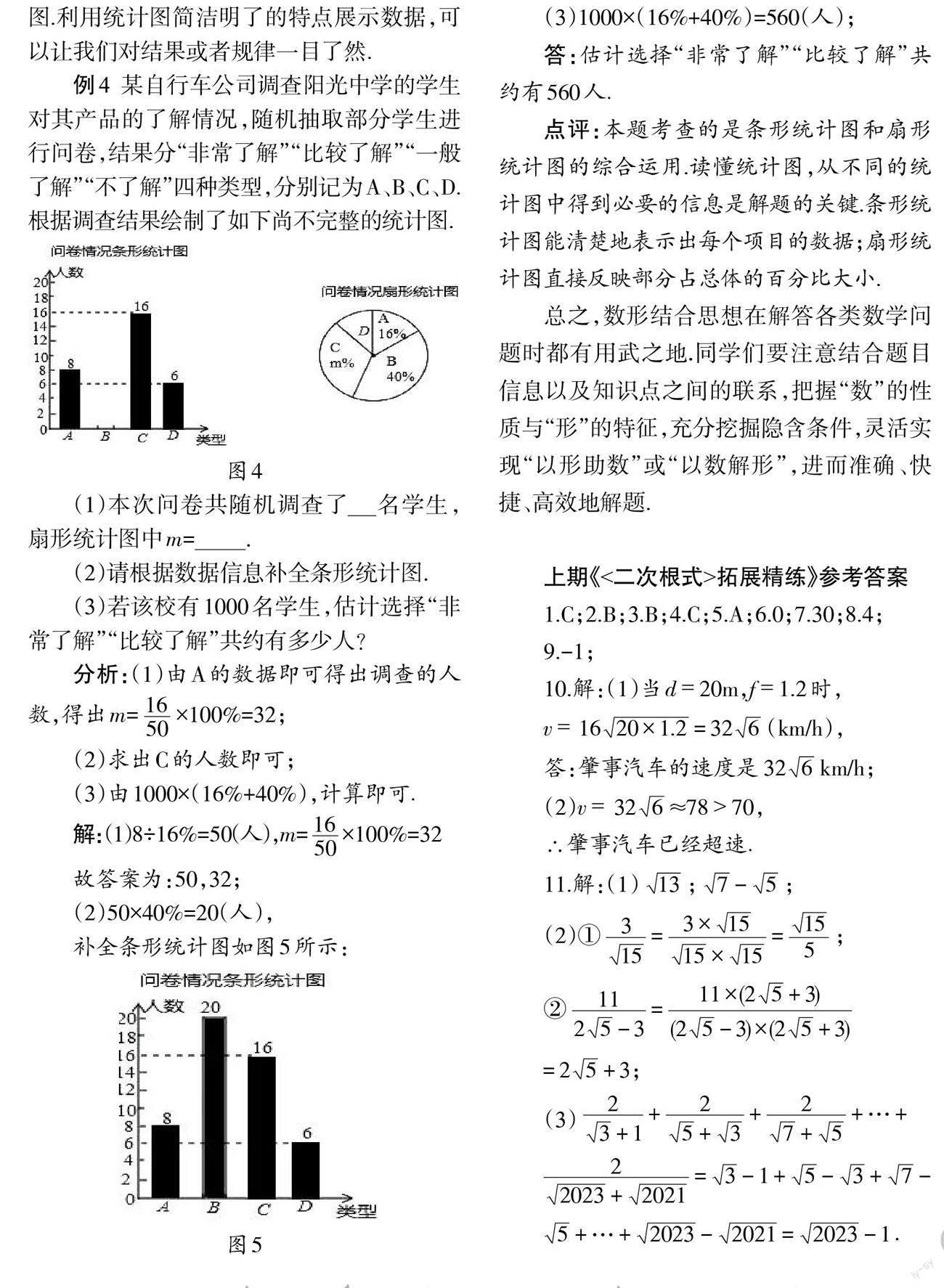
例4 某自行车公司调查阳光中学的学生对其产品的了解情况，随机抽取部分学生进行问卷，结果分“非常了解”“比较了解”“一般了解”“不了解”四种类型，分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图.

（1）本次问卷共随机调查了名学生，扇形统计图中m=．

（2）请根据数据信息补全条形统计图．

（3）若该校有 1000 名学生，估计选择“非常了解”“比较了解”共约有多少人？

点评：本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图，从不同的统计图中得到必要的信息是解题的关键.条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小.

总之，数形结合思想在解答各类数学问题时都有用武之地.同学们要注意结合题目信息以及知识点之间的联系，把握“数”的性质与“形”的特征，充分挖掘隐含条件，灵活实现“以形助数”或“以数解形”，进而准确、快捷、高效地解题.