论数形结合思想在小学数学课堂教学中的应用

郑平芳

［摘  要］ 在小学数学课堂教学中，要充分应用数形结合的思想，以“形”助“数”，可以简化数学问题，促进学生对数学知识的深化理解。数形结合思想在小学数学课堂教学中的应用通常有三种策略：一是以“形”的直观促进“数”的体会，增强概念理解；二是以“形”的形象启迪“数”的计算，深化算理剖析；三是以“形”的具体推动“数”的思考，呈现数量关系。

［关键词］ 数形结合；小学数学；课堂；教学；应用

小学生的空间思维和逻辑思维还不够成熟，常常会对枯燥的数学学习产生厌烦的心理。在小学数学课堂教学中，要充分应用数形结合的思想，以“形”助“数”，可以简化数学问题，激发学生的数学学习热情，提高学生的思维灵敏度，促进学生对数学知识的深化理解。既然数形结合与小学生的认知水平相符，而且对学生的数学学习有极其重要的作用，那么该如何巧妙运用呢？

一、以“形”的直观促进“数”的体会，增强概念理解

数学概念抽象性强，小学生由于身心发展的因素，往往無法透彻地理解概念。倘若按照传统教学方式施教，很难让学生全面而深刻地理解抽象的数学概念。因此，需要适时关注学生的身心发展，借助数形结合的思想，以“形”的直观促进“数”的体会，以此增强学生对数学概念的理解。与此同时，需要适时启发学生的想象，使其将已有知识经验和生活经验进行联通，实现对数学概念全面深度的解读。

以“形”的直观促进“数”的体会，增强概念理解，其实就是借助直观形象模型，理解抽象的数学概念，助推学生探究、感知和深化数学概念。对此，通常应做到“三个需要”：

一是引入数学概念时，需要图形演示。在引入数学概念时，把数和形结合起来，把抽象的概念和形象的图形联系起来，把概念的本质属性用图形演示出来，不但可以帮助学生丰富感性的材料，而且可以帮助学生奠定建构概念的基础。

二是形成数学概念时，需要借形设问。数形结合，“数”是数学概念知识，“形”是数学问题的背景。借形设问，就是借助问题的情境，显示数学问题的形象性，引导学生观察、分析、比较、抽象和概括，启迪学生的思维，保障概念的形成。

三是揭示数学概念时，需要画图体验。小学生的生活经历少，要他们凭借生活经验，变实际问题为数学问题，有相当大的难度。因此，需要根据教学内容的实际，引导学生用画图工具画图。通过画图，建立表象；通过画图，领悟概念；通过画图，揭示概念；通过画图，发展空间观点；通过画图，体验数形结合。

案例1  认识小数

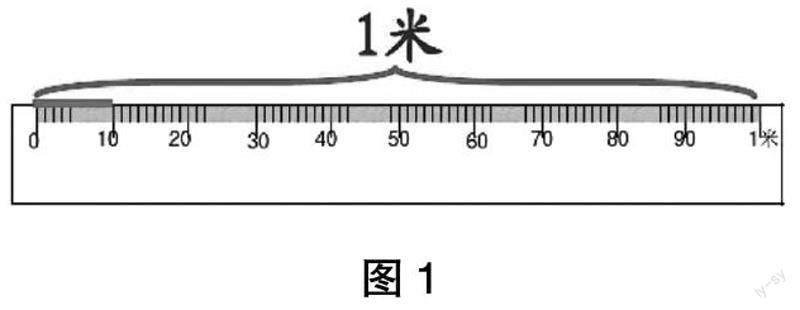
师：大家看，老师手中是什么？（教师出示米尺的直观图，见图1）

生（齐）：米尺。

师：不错，这是一把米尺，现在将它平均分成10份，每一份是……

生1：1分米。

生2：1/10米。

生3：0.1米。

师：非常好，生3所述的0.1米中的0.1是1个一位小数。下面，谁能说一说你们对一位小数的认识。

生4：分母是10的分数。

生5：其值在0到1之间。

师：那现在需要测量比1米长的物体，该怎么办？

生6：可以再接上一把和它一样的米尺。

师：非常不错的建议，大家看，这是多长？（出示两把米尺连接的图示，并指着第二把米尺2分米的位置）

生7：1米2分米。

师：现在需要测量很长的物体，让我们再接上一把米尺，这是多长？（又连接上一把米尺，并指着第三把米尺8分米的位置）

生8：2米8分米。

师：刚才所说的1米2分米和2米8分米，你们会用小数表示吗？

生9：1.2米和2.8米。

师：非常好，看来我们已经知道了值的区域。

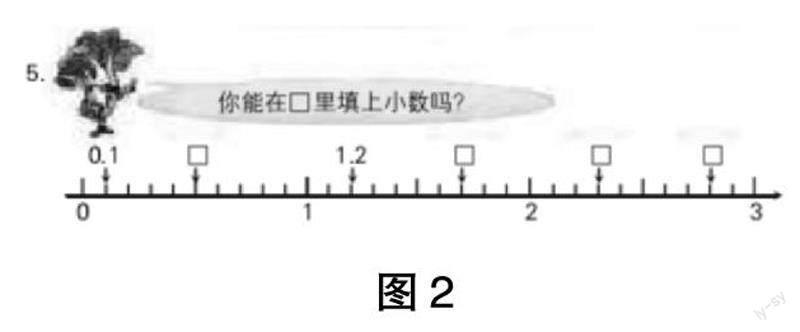
师：下面，我们一起来看图2所示的数轴，并试着完成本题……

数轴教学时可以自然渗透数形结合的数学思想，让学生感知到数轴上点与数的一一对应关系。然而，直接抛出数轴，学生可能无法抽象感知。教师不失时机地展示数轴的“前身”，通过实物米尺帮助学生对数轴形成初步感知。随着米尺的出现，教师巧妙地融合整数部分为0的小数与整数部分不为0的小数，为学生提供更加直观的体验，让学生清楚地掌握小数值的大小区域，增强对小数概念的理解和认识，从而向学生自然渗透数形结合的数学思想。

二、以“形”的形象启迪“数”的计算，深化算理剖析

引导学生学习数学，目的之一是为了让学生有一双数学的眼睛，有一个数学的头脑。学生会用数学的眼睛观察，会用数学的头脑思考，这是学生发展和生存必备的数学素养。以“形”的形象启迪“数”的计算，深化算理剖析，这就既要让学生了解“计算方法”的来龙去脉，又要让学生弄清“计算方法”的基本道理，让学生觉得数学计算不是冰冷的、干瘪的、枯燥的，而是热烈的、丰满的、滋润的。因此，教师在数学教学中要让学生明白“算理”与“算法”的孰重孰轻。有的教师在数学的计算教学中，误认为算理可有可无，抛开算理计算照样进行。于是，在数学教学中教师只是让学生尽快知道计算方法，再用大量的重复练习跟进。这样进行数学的计算教学，虽然见效快，但时间一长，学生就会忘记。显而易见，计算教学中的“算法”，不能蜻蜓点水、走马观花、急功近利，应该引导学生借助图形，深化对算理的剖析。只要深化了对算理的剖析，计算方法自然就会瓜熟蒂落、水到渠成、迎刃而解。

数学算理十分抽象，不易理解、记忆和掌握。然而在整个小学阶段，“数的运算”占有很大的比重。数形结合具有生动、形象和直观等优势，在小学数学教学中，以“形”的形象启迪“数”的计算，有利于学生深化算理的剖析。

案例2  一个数乘分数

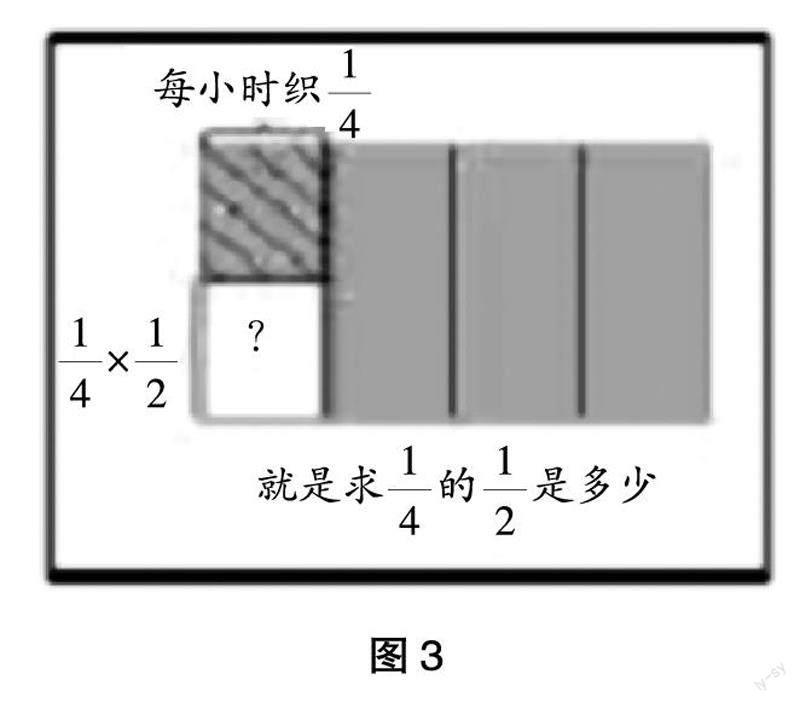
计算：1/4×1/2。

师：我们不着急计算，先动手折一折，并告诉老师1/4×1/2表示的是什么，好不好？（学生动手操作，教师巡回指导）

师：刚才看了大家的折出的1/4×1/2，尽管折法各不相同，但本质却是一致的。这里的1/4是谁的1/4？1/2呢？大家请看图3，从中你发现了什么？

生1：1/4×1/2就是求1/4的1/2。

师：很好，阐述简洁，理解正确！下面，请大家再来探索1/4×2/3。（学生又一次进行热烈地探索，教师巡视）

生2：如图4，这是我根据之前的探索得出的结论。

师：生2真是会动脑筋的好孩子，居然在这么短的时间内完成了迁移应用。其他人理解了吗？

生（齐）：理解了。

师：很好，我们来说一说3/4×2/3表示的是什么意思？

生3：就是求3/4的2/3是多少。

师：那a×（ ）/（ ）表示的是什么？

生4：表示的是a的几分之几是多少。

……

本例中，先通過“折”让学生建立表象，再利用数形结合让学生触摸精神内核，从而轻松理解算理，为之后掌握计算方法奠定了良好的基础。当然，学生对算理的理解无法一蹴而就，但有了数形结合的助力，就让学生的思考和知识内化有了依托，就让其认知结构的完善更加自然。学生是富有创造性的个体，有了教师的引导，自然就能借助图形拾级而上，促进数学观念的形成，真正理解和掌握算理。

三、以“形”的具体推动“数”的思考，呈现数量关系

数形结合就是把抽象的数学语言和直观的几何图形结合起来，把问题的数量关系和图形位置关系结合起来，达到“以形助数”或“以数解形”。数形结合可以借助简单图形、符号和文字合成的示意图，促进学生的具体形象思维和抽象逻辑思维协调发展，把数学知识之间的联系加以沟通。数形结合能让数学问题中的数量关系凸显出最本质的特征，能使数学问题中的数量关系变得直观。在解决数学问题的过程中，根据具体数学问题的情形，变图形问题为数量关系的问题，或变数量关系的问题为图形问题，可将抽象的数学问题具体化，复杂的数学问题简单化，从而化难为易，优化解决问题的途径。

在小学数学教学中，应用数形结合思想，以“形”的具体推动“数”的思考，呈现数量关系，有三个得天独厚的优势：一是小学数学教材中数形内容的编排，是由易到难、螺旋上升、交替呈现，这为应用数形结合思想提供了可能；二是小学生处在数学学习的初始阶段，学生头脑中对于数与形的分离符并不明显，是学生建构数形结合思想的最佳时期；三是小学生的身心特点决定了小学生的学习特点，小学生的思维是由直观形象思维逐渐向抽象逻辑思维过渡。数形结合正是小学生直观形象思维向抽象逻辑思维过渡的一种媒介，这种媒介便于小学生借助形的形象思考数的抽象，利用数的抽象提升形的内在逻辑，从而发现数量关系。

众所周知，小学生往往以形象思维为主，直观形象的图形更能帮助他们理解数学问题。在实际教学中，不少学生由于难以自主地沟通“数”与“形”，出现做题难、慢、错的状况，使得高效教学成了泡影。合理利用“形”的具体，推动“数”的思考，可以清晰呈现一些复杂的数量关系，促进学生的深度思考与探究，提高学生的解题速度和能力。

案例3  鸡兔同笼

问题情境：一些鸡和兔被关在一个笼子里，数一数，共有头5个，共有腿14条，笼子里有几只鸡？几只兔？

师：你们有想法了吗？

生1：2只鸡，3只兔。

生2：不对，是3只鸡，2只兔。

师：这一定是你们猜想后的想法，既然有了争议，我们何不画图来促进思考呢？（学生立刻投入画图的活动中，教师巡视，并拍下有效信息）

师：我们一起来看一看刚才大家的思考过程。（教师课件展示部分学生的画图过程）

师：请这几名学生分别说一说你们是怎么思考的？

生3： 我是先画了1只鸡和1只兔，数一数；接着又画了1只鸡和1只兔，再数一数；就又画了1只鸡，得出结果一共3只鸡和2只兔。

生4：我是全部画成了鸡，发现腿不够，然后就把1只鸡改成了兔，还是不够，又把1只鸡画成了兔。

生5：我是全部画成了兔……

师（微笑）：你们的想法都很有创意……

由于鸡兔同笼的问题在现实生活中很难探找到原型，从而造成学生理解困难。大部分教师会选择中高年级学生来施教，而执教者却大胆借用二年级学生进行施教。从整个教学过程可以发现，教学之所以比较成功，主要源于教师的提议“画图来促进思考”，为学生之后的一系列思考提供了很好的方向。学生在画图时各显神通，充分施展自身的创造潜能，让看似复杂的问题得到顺畅的解决。就这样，复杂的“鸡兔同笼”问题，在执教者的精心设计下，变得简单而具体。这样的深度思考，能让学生的思维灵动起来，能极好地提高学生的学习兴趣，培养学生的数学能力，使课堂教学事半功倍。

总之，“形”的直观可以为学生提供恰当的形象材料，可以让抽象的知识形象化，不仅利于学生高效学习数学知识，还利于让枯燥的数学学习充满乐趣。因此，教师在教学中应适切利用好数形结合这一手段独特的优势，帮助学生理解概念、明晰算理、理清数量关系，促进学生的形象思维和逻辑思维全面发展，为学生的可持续发展奠定良好而扎实的基础。