点动成线，线动成面，面动成体

［摘  要］ 教师只有在理解数学知识的基础上，把握学生的认知基础，通过精心创设问题情境，精准把脉知识的发生、发展过程，才能与学生产生共鸣，从而突破重、难点，提升学生的思维能力. 在教学过程中，以情境教学为起点，以教学任务为走向，以问题设计为驱动，以问题解决为目标，架构知识教学联结性，可以使学生在潜移默化中习得知识，这也体现了学科的育人价值.

［关键词］ 问题情境；问题关联；问题解决；知识生成；思维发展

“线段的垂直平分线的性质”是人教版八年级上册13.1.2的内容，教学这一内容时，要促进学生知识合理生成，促进学生思维合理发展，对一线教师来说并不容易，教学这堂课对教师来说都是一个不小的挑战. 笔者受邀观看一区级赛课，其中一位选手获得了一致好评，现将这堂课的教学过程整理出来，并阐述自己的一些思考.

基本情况分析

1. 教学内容及解析

本节内容有线段的垂直平分线的性质、线段的垂直平分线的判定、线段的垂直平分线的集合定义以及尺规作图. 在此之前，学生已经学习了全等及轴对称的相关知识，知道了轴（成轴）对称的定义、线段的垂直平分线的定义以及轴对称的性质，本节内容是在学生前面所学知识的基础上，进一步研究线段的垂直平分线的性质，能为后面学习画轴对称图形、等腰三角形以及最短路径问题打基础. 因此，本节课的学习能为学生的系统学习、更好地梳理知识起到铺垫作用. 由此，可将本节课的教学重点确定为：线段的垂直平分线的性质和判定.

2. 教学目标及解析

本节内容的教学目标为：（1）理解并掌握线段的垂直平分线的性质和判定定理，了解线段的垂直平分线是到线段两端点距离相等的点的集合；（2）会利用线段的垂直平分线的性质及判定定理进行简单的推理、计算.

达成上述目标的标志是：（1）通过实际操作，经历线段的垂直平分线的性质和判定定理的形成过程；通过观察、探究、猜想、证明，构建线段的垂直平分线的性质和判定定理；借助信息技术形象感知线段垂直平分线的集合定义. （2）学生能够在合作探究及展示的过程中大胆表达，最终解决问题，体验用数学的眼光看待事物，发展学生的演绎推理能力.

3. 教学问题诊断分析

本节课的教学是基于学生对事物的基本认识过程而设计的. 学生在上一章已经学习了三角形的全等和角平分线的性质，这些知识能为线段的垂直平分线性质的学习做好知识准备. 本章第一节“轴对称”的学习，使得学生对线段的垂直平分线的学习有了一定的认识，但由于线段的垂直平分线的判定比较抽象，学生难以理解，所以教师教学时应深入浅出地讲解. 理解“线段的垂直平分线是到线段两个端点的距离相等的点的集合”需要建立在对线段的垂直平分线的性质和判定的理解基础上，所以难度较大，由于学生没有轨迹的概念，因此理解起来很困难，故教学时要求教师结合图形进行说明. 由此可将本节课的教学难点确定为：线段的垂直平分线的判定以及线段的垂直平分线的集合定义.

教学过程展示

1. 情境引入，激活思维

师：（引入语）古人说，“凡事预则立，不预则废”. 在每个人的心中，都有一座美丽的校园，你们想设计一下吗？现在，和老师一起，拿起你面前的白纸，一起来规划这座美丽的校园吧！

师：我们折叠这张纸，使得下方和这张纸的右边重合，再在折出来的图形上用笔任意取一个点，不妨设为A点，这个点就是我们要修建的图书馆的位置. 把这张纸展开，我们就得到了一个与点A对应的点，假设为点B，这个点是我们要修建的教学楼的位置，这条折痕是我们学校的主干道，我们用l来表示. 连接AB，根据前面所学的知识，我们知道l是线段AB的垂直平分线.（如图1所示）

师生活动：教师在黑板上现场展示，学生跟随教师的节奏自己动手操作.

教学分析  创设问题情境能调动学生的参与积極性，能引发学生的认知冲突  ［1］. 学生只有经历知识产生的过程，才能感悟知识的实质. 教学时，教师不仅要让学生明白“学什么”，还要让学生明白“为什么学”，这样学生才能真正地领悟线段的垂直平分线的性质与判定. 教师进行情境教学的素材来源于学生熟悉的事物，这正是学生思维的触发点，能激发学生的学习兴趣，且教师在教学过程中将情境的创设指向学习目标，这就能引发学生的探究兴趣，能为接下来的高效教学开路.

2. 感受新知，探究本质

问题1：在l上任意取一点P，连接PA，PB，比较PA和PB的长短.

追问1：比较两条线段的长短，有哪些方法？

追问2：类比学习角平分线的性质，我们可以先测量线段的长度. 请同学们用直尺测量PA，PB两条线段的长度.

追问3：除了测量，你们还有其他比较线段长短的方法吗？（众生：证全等）

追问4：一会儿我会专门介绍这个方法. 大家发现了吗？一开始我们在折纸，翻折一下，PA和PB能重合吗？

追问5：人工操作往往存在误差，因此我们可以借助计算机来进行验证. 已知线段AB， l是线段AB的垂直平分线，现在我们在l上任意取一点P，连接PA，PB，大家看看PA和PB是否相等. （几何画板具有度量功能，能测量出PA，PB的长度）

追问6：现在我们让点P在l上移动，请大家观察PA，PB的长度是否依然相等.

追问7：通过实验，我们可以猜想，线段的垂直平分线上的点到线段两端点的距离？

生：相等.

师：现在，请同学们在学案上写下我们的猜想.

师生活动：学生跟随教师的节奏，通过动手测量、翻折、几何画板度量、直观感知等操作，初步感知了线段的垂直平分线的性质，引发了学生探究线段的垂直平分线的性质的欲望.

教学分析  观察、猜想、证明等数学活动，是学生理解性质的必备过程，且探究过程应进一步体现数学知识生成的合理性. 学生通过测量、翻折、几何画板度量、直观感知等操作，加深了对性质探究过程的理解，促进了思维的合理发展.

問题2：刚才有同学提到可以通过全等来证明PA=PB，现在我们就通过几何证明来验证. 要想证明全等，我们得先找到已知和求证，已知是什么？

生：l⊥AB，AC=BC（C为AB的中点）.

追问1：我们再严谨一些，要加上点P在l上，求证的是什么？

生：PA=PB.

追问2：证明全等需要几个条件？

追问3：要证明全等，现在我们有几个条件？

追问4：要证明全等，我们还差哪一个条件？

追问5：我们知道点P是l上任意一点，那点P在l上运动时，P，C，A三点一定会构成三角形吗？

追问6：我们现在证明的是点P不在线段AB上，那点P在线段AB上的情形呢？

例1  如图2所示，在△ABC中，AB的垂直平分线交AB于点E，交AC于点D，连接BD.

（1）若AD=9 cm，则 BD=____cm；

（2）若AC=20 cm，△DBC的周长为35 cm，则BC的长为____cm.

师生活动：教师引导学生验证猜想PA=PB，并板书证明过程. 此过程由师生共同完成. 接下来教师指导学生完成例1，过程中师生齐答，教师则展示解答过程.

教学分析  教师引导学生论证性质，逐渐将线段的垂直平分线的学习引向深入，从而加深学生对性质的理解. 在进行推理的过程中，教师运用分类讨论思想，完善了对性质的证明，培养了学生严密的逻辑思维能力.

问题3：现在我们将这个性质的条件和结论互换位置，换位置后还成立吗？也就是到线段两端点的距离相等的点在这条线段的垂直平分线上吗？

追问1：我们解决例1时得到了AD=BD，反过来，如果AD=BD，那点D在线段AB的垂直平分线上吗？

追问2：怎么证明？

生：作辅助线.

追问3：因为我们要证明的结论中有两部分，一是垂直，二是平分，所以可以利用辅助线，先给出其中一个结论，再证明另一个结论. 比如取AB的中点E，此时DE就是 AB边上的中线（如图3所示），那现在我们只需要证明什么？

生：证明垂直.

追问4：要证垂直，也就是证∠AED=∠ BED，可以采用什么方法？

追问5：当然，也可以过点D作AB边的高线DE（如图3所示），那现在只需要证明什么？用什么方法证明？

师生活动：教师不断追问，完成对线段的垂直平分线判定的证明. 教师展示证明过程，完成文字语言和符号语言的书写.

教学分析  线段的垂直平分线的判定抽象程度较高，学生理解晦涩，在本堂课中，教师并没有采用常规的方法——将性质的条件和结论倒置，引导学生证明，而是充分挖掘例1的价值，将学生置于具体的问题情境中，通过由具体到抽象的思路，引导学生逐步完成对判定的证明. 学生完成例1轻而易举，教师引导学生再次挖掘，学生突破判定不再费力.

3. 合作探究，集思广益

例2  如图4所示，AD=BD，AP=BP，DP与AB交于点E，证明：DP⊥AB，AE=BE.

师生活动：教师展示例2，学生分小组讨论，教师适时辅导，学生整理出结果后分小组展示. 多数学生利用“SAS”来证明结论，教师引导学生通过线段垂直平分线的判定定理来解决问题.

教学分析  学生小组合作探究，运用已有知识来思考并解决问题，逐渐形成知识共同体. 教师同时参与讨论，给出中肯的建议与评价，帮助学生进行更深入的学习，渗透了“以解决问题为目标，以加强学生学习主动性为原则，以学习过程互动化为手段”的核心思想   ［1］. 学生利用全等三角形来证明，教师在肯定学生讨论结果的同时，引导学生利用刚才学习的线段的垂直平分线的判定来解决问题，培养了学生应用知识的能力和思维发散能力.

问题4：例2中有两个点到线段AB两端点的距离相等，还能找到更多的点吗？

追问1：现在我们要去找等线段，仍然可以借助圆规. 任意取一个大于线段AB一半的半径，即半径大于 AB，再分别以A，B两点为圆心画圆弧，它们的交点到A，B两点的距离相等吗？

追问2：改变半径，再分别以A，B两点为圆心画圆弧，这时我们又得到一个交点，这个交点到A，B两点之间的距离相等吗？

追问3：同样地，我们也可以在线段AB的下方找到点（教师边说边演示），这个点到A，B两点之间的距离相等吗？（如图5所示）

追问4：运用同样的方法我们可以找到很多这样的点，这些点到A，B两点之间的距离相等吗？（如图6所示）

追问5：它们是怎样的一条轨迹？

师生活动： 教师利用圆规进行演示，学生观察并回答；教师再借助几何画板动态演示，学生发现这些点构成了一条直线，接下来教师引导学生总结出“线段AB的垂直平分线就是与线段A，B两个端点距离相等的点的集合”.

教学分析  如何认识线段的垂直平分线的集合定义，是本节课的难点. 关于把一个几何图形看成是满足某种条件的点的集合的思想，在教学角平分线时已有渗透，所以教学本课时，教师循序渐进，让学生认识到，把一个图形看成满足某种条件的点的集合，必须符合下面两个条件：①图形上的每一个点都满足某个条件；②满足这个条件的每一个点都在这个图形上. 通过几何画板的动态演示，教师将抽象问题直观化，学生不仅加深了对知识的印象，而且提升了思维能力.

4. 新知应用，启思明智

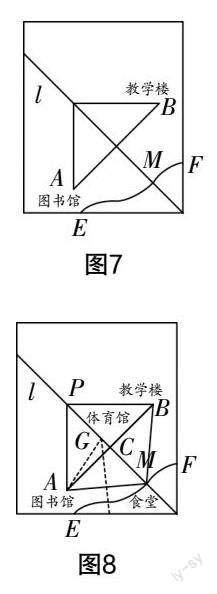
问题5：同学们，现在我们带着这节课学习的内容，继续完成学校的设计. 现在有一条小道EF（教师在图中画出小道，边画边提问，如图7所示），我们要在小道EF上找一个点修建食堂，使得食堂到A，B两点的距离相等，那食堂应该建在哪儿呢？

追問：我们还想修建一个体育馆，使得体育馆到图书馆、教学楼和食堂的距离都相等，你能找到体育馆的位置吗？

师生活动：学生根据教师的提问回答，教师在黑板上展示（如图8所示）；学生思维受阻时，教师给予适时、适当的点拨.

教学分析  学生此前已经经历了操作、猜想、证明、应用的过程，得到了线段的垂直平分线的判定定理，这里通过“建食堂”，让知识活学活用，提升了学生解决问题的能力；通过“建体育馆”，变式问题，提升难度，要求学生熟识问题本源，培养了学生的类比迁移能力和发散思维能力. 利用交轨法确定某个点的位置，让知识回归本源——数学源于生活，又应用于生活. 实际上，将知识转化为能力的主要途径是操作，在操作中，学生得以体验、感悟，形成新的稳定的心理特征，再通过新的情境问题，能力得以增强，并形成新的能力结构.

5. 小结巩固，提升思维

问题6：通过这节课的学习，你们学到了哪些知识？

师生活动：学生发言，教师结合学生的发言进行补充，最后教师总结、布置作业.

教学分析  教师适时的形成性评价和终结性评价，有助于学生及时了解自己学习过程中存在的问题，能为学生的后续学习奠基.

教学感悟

1. “点动成线”——问题情境，建构情境教学整体性

对于本课时的教学，教师从学生熟悉的情境出发，易于激发学生的兴趣，能提高学生的课堂参与度. 整堂课的教学围绕情境问题“校园设计”展开，这是第一条主线，体现了“数学问题情境化”，情境引入不突兀，情境搭建自然，情境应用科学合理. 本节课的点睛之笔在最后——寻找“体育馆”，即寻找两条垂直平分线的交点，学生的探究兴趣一下子被调动起来，这种以情境问题搭建变式训练的教学方式，能让学生学会把新的问题转化为已有知识经验来解决，从而提升学生解决问题的能力. 本课时的教学，以生活情境为起点，以教学任务为走向，以问题设计为驱动，将课时目标的达成融于情境教学当中，注重发挥学生的主观能动性，使学生在潜移默化中习得了知识.

2. “线动成面”——问题关联，架构知识教学联结性

本节课的第二条主线是“情境问题数学化”. 本课时要解决的数学问题有三：一是线段的垂直平分线的性质，二是线段的垂直平分线的判定，三是线段的垂直平分线的集合定义. 教师通过课堂“情境问题数学化”，将生活实际问题引入数学，让学生倍感亲切. 接下来，学生通过完成例1，加深了对线段垂直平分线性质的理解. 在此基础上，教师继续挖掘例1的价值，通过条件和结论互换，引导学生发现并总结线段的垂直平分线的判定定理. 紧接着，教师在例1的基础上通过增加条件，向学生出示例2，学生则通过合作探究，得出结论，教师顺势而导，引导学生得到“线段的垂直平分线是与线段两个端点距离相等的点的集合”. 由于几何思维是依据图形产生的，所以教学线段的垂直平分线的集合定义时，教师动手画图，并借助几何画板进行验证，通过不停地变化，引导学生借助图形进行直观思考和分析，并进行逻辑推理活动，使得本节课的教学目标得以顺利达成，学生的逻辑思维能力得以提升. 问题是数学的核心，问题解决就是数学教与学的关键  ［2］ . 可以说，本节课，“情境问题数学化”这条主线是建立在例1的基础上完成的，教师以问题关联的形式，由浅入深，由低级到高级，架构了线段的垂直平分线的相关知识，促使教学达到了“由一题，会一类”的效果.

3. “面动成体”——问题解决，关注课堂教学知识发展过程的合理性、学生思维过程的合理性及课堂教学的合理性

数学教学的基础是理解数学、理解学生、理解教学. 理解数学，就是精准把脉知识的发生、发展过程. 教师只有在理解数学知识的基础上，通过预设逻辑主线，精心创设问题，才能揭示知识的内在发展本质，使学生关注知识发展过程的合理性，从而突破重、难点. 理解学生，就是理解学生当前学习期的认知特点和认知规律，把握认知基础 ，准确定位，这样才能立足于学生的最近发展区，根据学生的学习经验、思维特点等，开展数学活动. 理解教学，就是以新课标为依据，以数学知识为主线，以核心素养为导向，以学生的认知为基础  ［3］，采取与之相匹配的教学策略与教学手段. 教师只有精准把脉学生的认知基础，注重预设与生成之间的关系，才能采取与之相匹配的问题解决策略，使学生的思维发展顺理成章. 对于本课例的教学，教师以情境“校园设计”为载体，在整个探究过程中，留给学生足够的时间与空间，让学生亲身经历“观察—探究—猜想—证明”的完整过程，感受证明的必要性. 同时，教师借助几何画板，让几何图形“动”起来，让学生有深深的代入感，促进了学生对线段的垂直平分线性质和判定定理的理解. 本节课，教师精心设计各环节的教学内容，突出了几何学习的主线，达到了“做一道，会一类”的教学目标，体现了学科育人的价值，对学生的长远学习有深远的意义.

参考文献：

［1］苏文涛. 基于CLES模型的问题解决教学探究［J］. 进展：教学与科研，2019（12）： 47-48.

［2］苏文涛. 信息技术下“问题解决导向式”教学模式浅谈［J］. 数学教学通讯，2021（11）：6-9.

［3］孙洁，朱月红. 合理设计探究活动  用数学的方式育人——“中心对称与中心对称图形”教学感悟［J］. 中学数学，2021（11）：8-10.