基于Simulink 的SPWM 逆变电路谐波分析

林 倩，杨姝玥，黄翔东

（1.青海民族大学 物理与电子信息工程学院，青海 西宁 810007；2.天津大学 电气自动化与信息工程学院，天津 300072）

0 引 言

随着电力电子技术的快速发展，逆变电路已广泛应用于光伏发电[1]、直流输电[2]、风力发电[3]等方面。当使用蓄电池、干电池、太阳能电池等直流电源向交流负载供电时，需要用到逆变电路[4]。此外，交流电动机变频调速器、不间断电源、感应加热电源等电力电子设备的电路关键部分均为逆变电路。而脉宽调制（Pulse Width Modulation, PWM）技术凭借其电路响应速度快、输出波形效果好、调频调压不受限于元件参数等特点，成为了逆变电路的核心技术[5]。

但在实际电网中，谐波可能会在电力系统的各个环节中产生[6]。以用电终端为例，由于自身固有的非线性特性，使其所产生的高次谐波依然是当前影响电网供电质量的主要因素[7]，这也引起了人们的广泛关注。目前，国内外已经有一些关于谐波分析的研究，如：2018 年，Kiyak 采用离散小波变换分析高谐波失真的电主轴发电机产生的电压信号，从而获得准确的基波分量幅值时间变化[8]；2020 年，N. H. Baharudin 等人基于瞬时无功功率理论来抑制配电系统非线性负载的电流谐波，使电流总谐波失真[9]小于8%；2023 年，叶宗彬等人利用滑窗离散傅里叶变换技术，在1 /6 个基波周期内实现了快速检测谐波，成功降低了谐波的检测延迟[10]。上述各类谐波的描述和分析对减少和抑制谐波的研究具有重要意义。

本文以SPWM 逆变电路为例，基于Simulink 实现双极性和单极性调制逆变电路的建模与仿真，并对比两者输出电压谐波性能的优越性，定量分析重要参数对单极性调制电路谐波成分的影响，从而充分把握谐波特性，以达到减少或抑制谐波的目的。

1 逆变电路的基础理论

1.1 电压型单相SPWM 逆变电路原理

PWM 控制是指对脉冲宽度进行调制的技术，通过调制不同脉冲宽度来等效合成所需要的波形信号[11]。例如，调制波由正弦波和三角波调制合成，其脉宽随正弦波规律变化而变化，能够控制逆变电路中一种非常重要的逆变器件，即绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor, IGBT），这种调制技术也被称为SPWM[12]。

SPWM 逆变电路分为电压型和电流型，其中最常用的是电压型SPWM 控制技术。本文使用的电压型单相桥式SPWM 逆变电路原理如图1 所示，直流信号为电压源Ud，由电阻R与电感L串联构成阻感性负载，全控型IGBT 功率开关器件V1~V4与二极管VD1~VD4并联，起反馈能量作用。此外，信号Ur与载波Uc通过调制电路控制IGBT 的通断，控制V1~V4四路驱动信号。

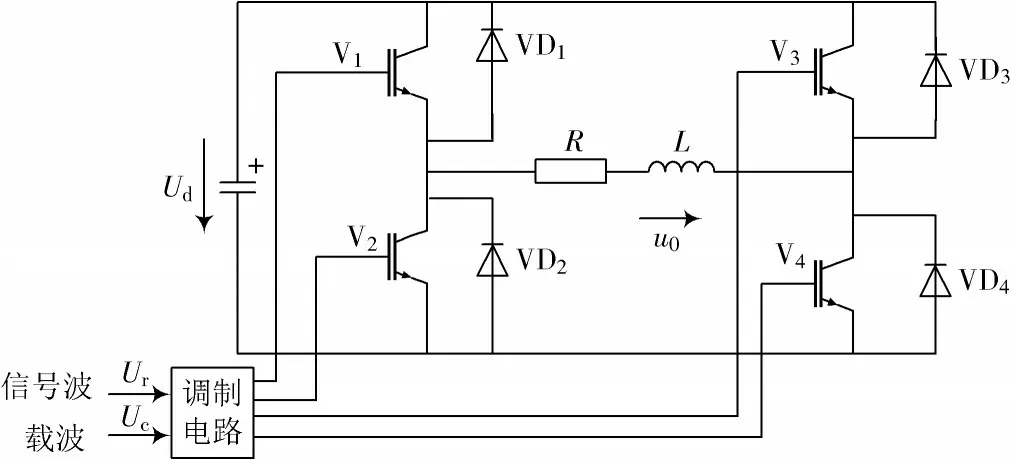
图1 单相桥式SPWM 逆变电路原理图

1.2 调制原理

调制度和载波比是SPWM 技术中两个重要的参数[13]，其中调制度M为正弦调制波参考信号幅值Urm与三角波幅值Ucm之比，也称调制比，公式如下：

载波比P为三角载波信号频率fc与正弦调制参考信号频率fs之比，计算公式为：

在实际应用中，SPWM 逆变器的输出基波电压常采用电压平均模型进行计算[14]。当载波信号频率远远高于输出电压的基频，且调制度M≤1 时，基波电压的幅值U1m为：

式中Ud为电压源的幅值。该公式对于SPWM 技术具有重要意义，它表明在M≤1、fc≫fs的情况下，SPWM 逆变电路输出基波电压的幅值与调制度呈“M”线性关系。因此通过控制调制信号，可方便地调控逆变电路输出电压的频率和幅值。再者，电压型逆变器输出电压的谐波通常分布在载波频率fc的整数倍周围，而且对第P次谐波分量影响最大（P为载波比）[15]。

2 Simulink 仿真及结果分析

为了分析谐波特性及验证理论，本文设计了对应的逆变电路，并对结果进行仿真分析，主要包括双极性SPWM 逆变电路仿真、单极性SPWM 逆变电路仿真和重要参数对单极性SPWM 逆变电路谐波成分的影响。

2.1 双极性SPWM 逆变电路仿真

利用Simulink 模块建立双极性SPWM 逆变电路模型。如图2 所示，整个逆变电路由控制电路和主电路组成，其中主电路的4 个桥臂由IGBT 搭建，阻感性负载由Series RLC Branch 搭建，并设置阻感性负载的电阻R为1 Ω，电感L为2 mH，直流电源幅值为300 V。同时，控制电路采用子系统封装的形式构造一个SPWM 发生器来控制主电路。

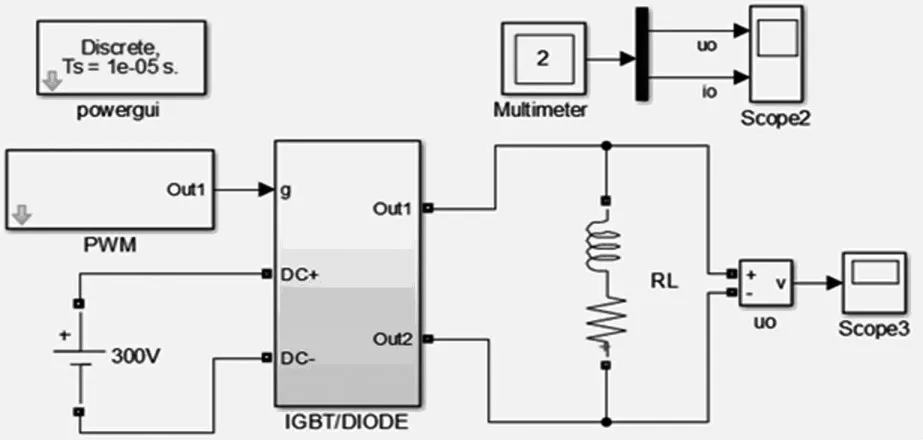
图2 SPWM 逆变电路模型

双极性SPWM 控制电路模型如图3 所示，其中等腰三角载波由Repeating Sequence 模块产生，正弦调制波由Fcn 函数与调制度相乘而得，Data Type Conversion 子系统将输出数据类型转换为双精度浮点型。通过设置合理的调制度和载波比，就可以采用Multimeter 测量模块得到输出电压。

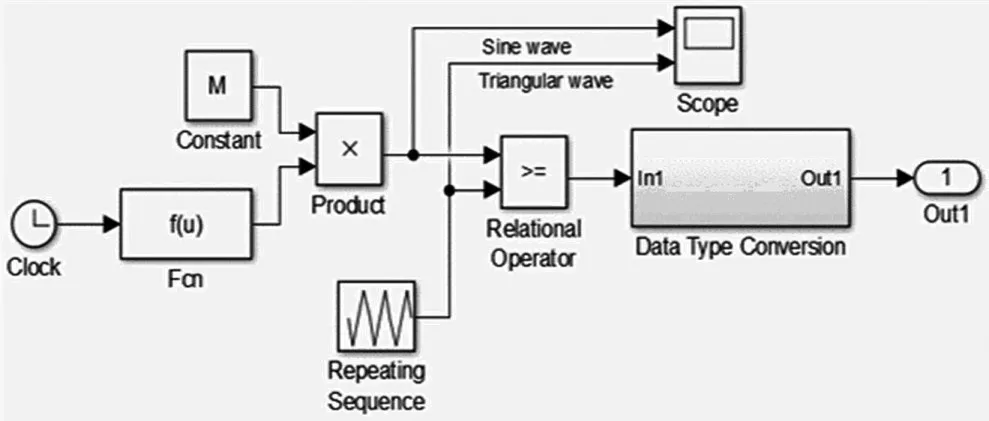
图3 双极性SPWM 控制电路模型

仿真结束后，得到的双极性调制前正弦波和三角波的波形如图4 所示，其中蓝色曲线是周期由载波频率决定的等腰三角波，黑色曲线是周期由调频比决定的正弦调制波。从图中可以看出双极性调制的特点，即PWM波形在半个周期中有正值和负值。

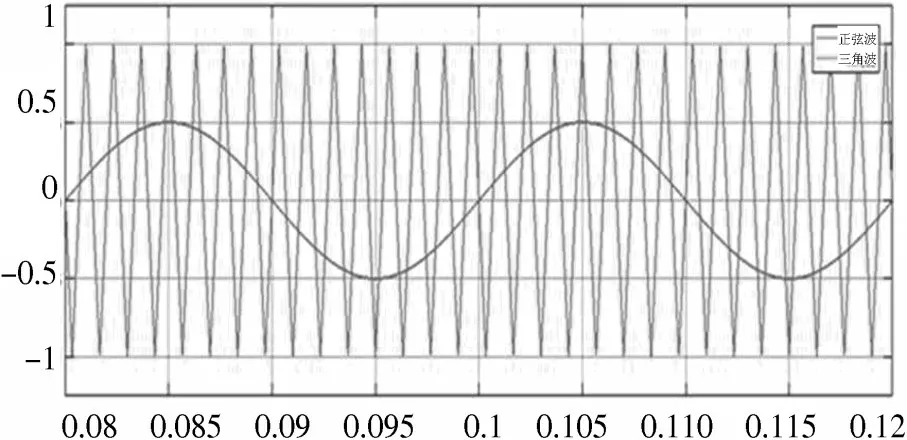
图4 双极性调制前正弦波与三角波的波形

接着，采用Specialized Power Systems 中powergui 模块实现电路元件和状态空间方程的连接与转换，并利用FFT Analysis 功能对输出电压进行傅里叶分析，具体分析结果如图5 所示。

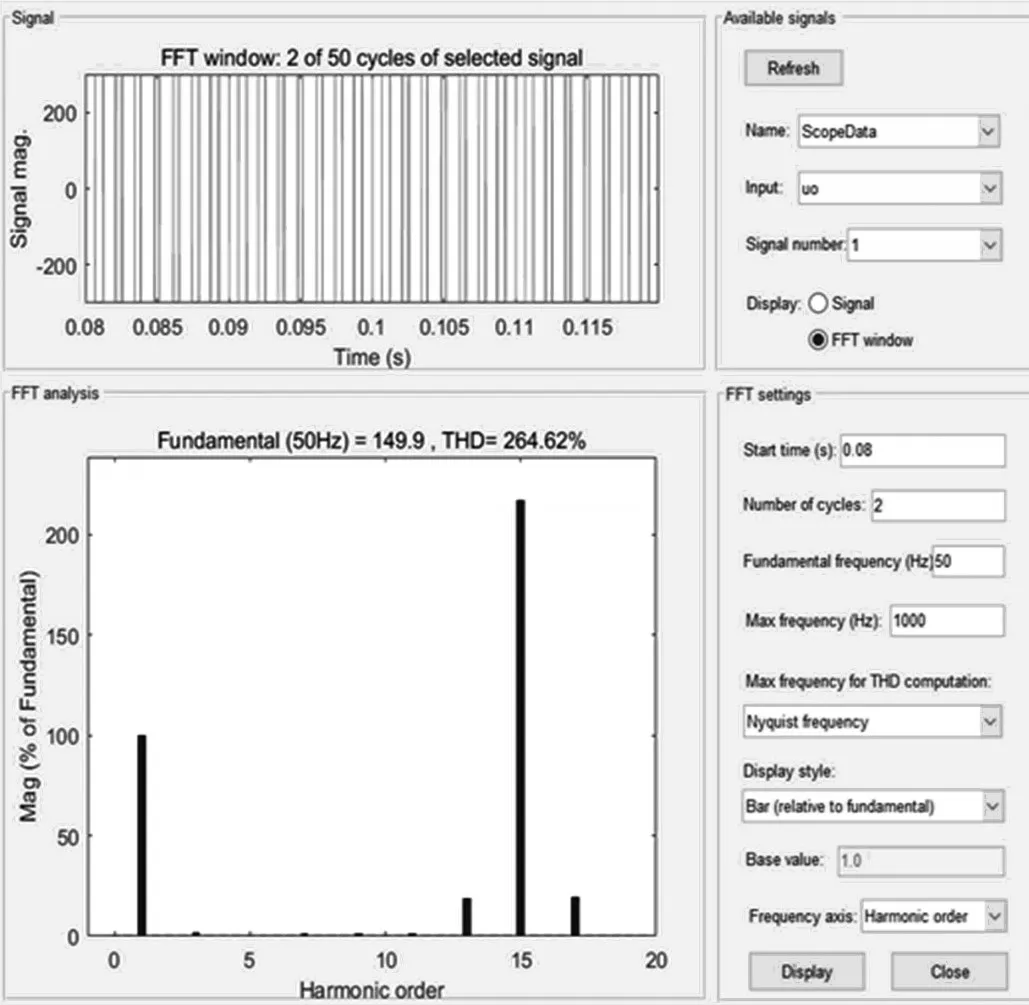
图5 M=0.5，P=15 时双极性逆变电路输出电压的FFT 分析结果

从图5 中可以看出，双极性逆变电路的基波电压幅值为149.9 V，与式（3）的理论值150 V 相吻合。在谐波当中，第15 次谐波最为严重，谐波分量已经达到了基波的2.16 倍，其次是第13 次谐波，总谐波失真为264.62%。

2.2 单极性SPWM 逆变电路仿真

建立单极性SPWM 逆变电路模型，其主电路与双极性相同，区别在于单极性控制电路模型更为复杂，具体模型如图6 所示。其中在等腰三角载波处乘以一个Square wave pulse子模块，通过将方波脉冲幅值增大2倍后加上常数1 获得；其余模块的参数设定与双极性逆变电路基本一致。

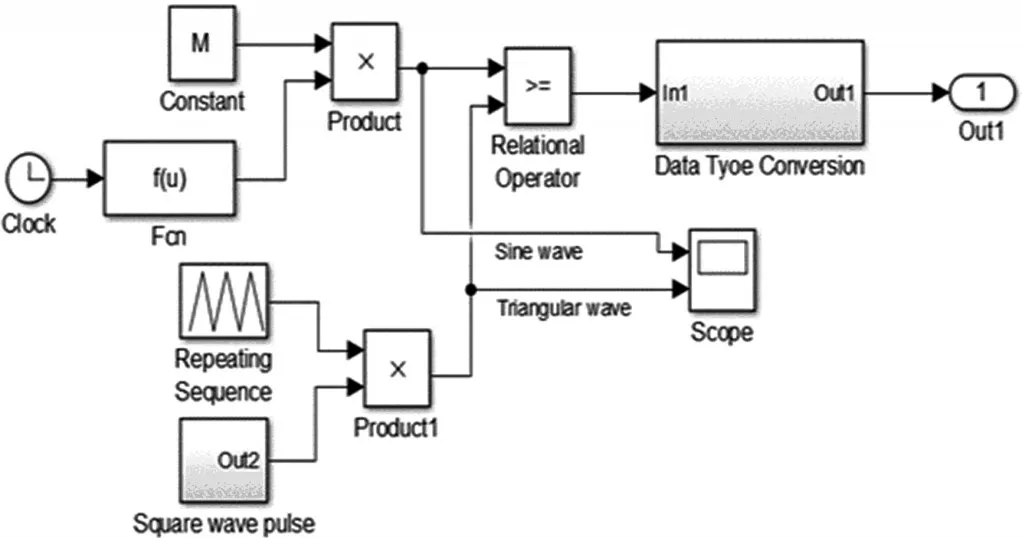
图6 单极性SPWM 控制电路模型

仿真结束后，得到的单极性调制前正弦波和三角波的波形如图7 所示，蓝色曲线仍为等腰三角波，黑色曲线仍为正弦调制波。

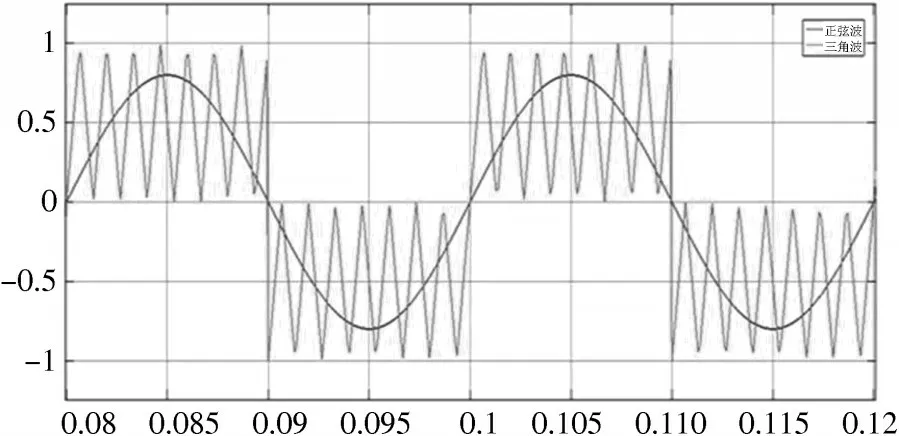
图7 单极性调制前正弦波与三角波的波形

图7 中单极性调制的特点是：PWM 波形在半个周期中只在单极性范围内变化。

同样对输出电压进行傅里叶分析，结果如图8 所示。结合图7 可知：当三角载波为正时，输出电压为正；当三角载波为负时，输出电压为负。此外，单极性逆变电路的基波电压幅值为151.4 V，接近式（3）的理论值，说明输出电压的基波幅值与调制度呈“M”线性关系。然而谐波分布与双极性相比有明显不同，不再含有开关次整数倍谐波，即第15 次谐波，第14 和16 次谐波分别为基波的71.54%和71.31%。值得考虑的是，最低次谐波为第12 次，其幅值为基波的10.11%，明显优于双极性调制的结果。此外，总谐波失真为122.81%，比双极性小了141.81%，这说明单极性逆变电路输入波形的失真程度较小，高次谐波所占分量较小。

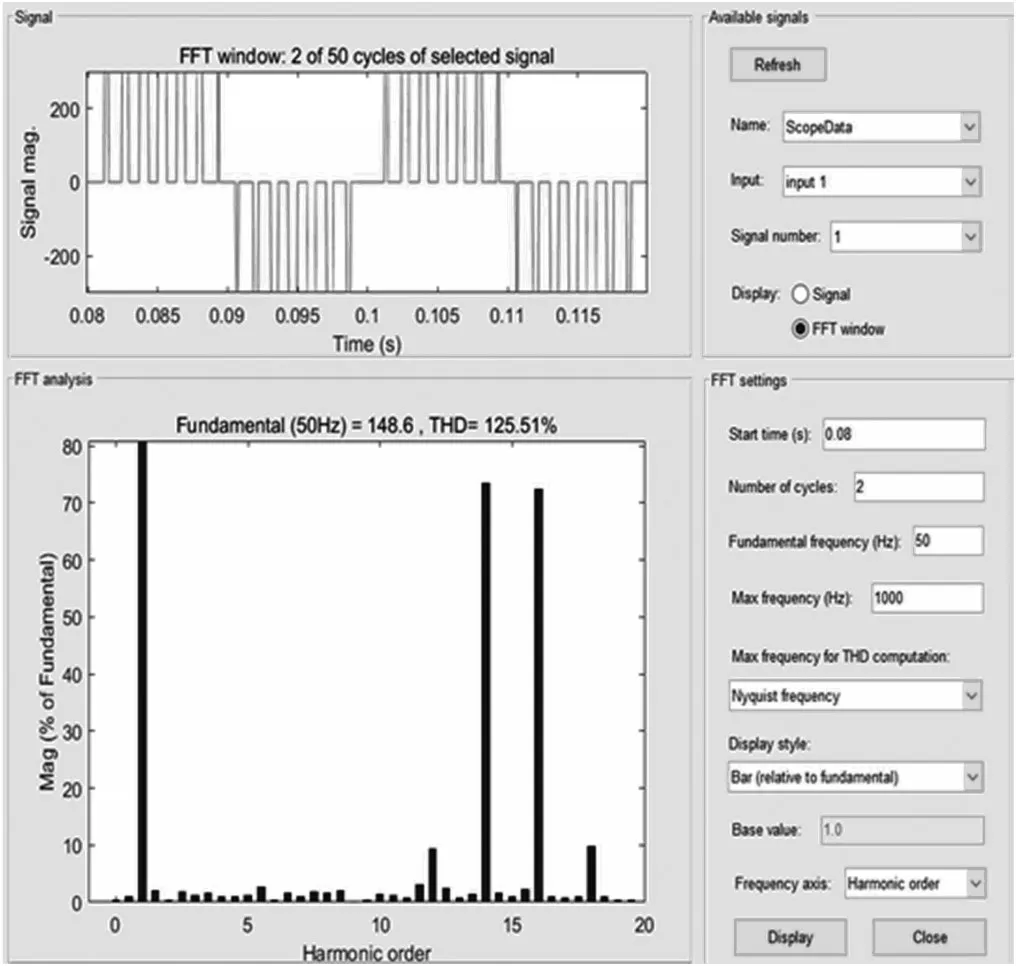
图8 M=0.5，P=15 时单极性逆变电路输出电压的FFT 分析结果

由此可见，在线性调制条件下，单极性调制时的谐波性能比双极性调制更具有优越性。因此，下文分析重要参数对单极性SPWM 逆变电路谐波成分的影响。

2.3 重要参数对单极性SPWM 逆变电路谐波成分的影响

本文将调制度设为0.8，载波比保持不变，得到的单极性逆变电路输出电压的FFT 分析结果如图9 所示。

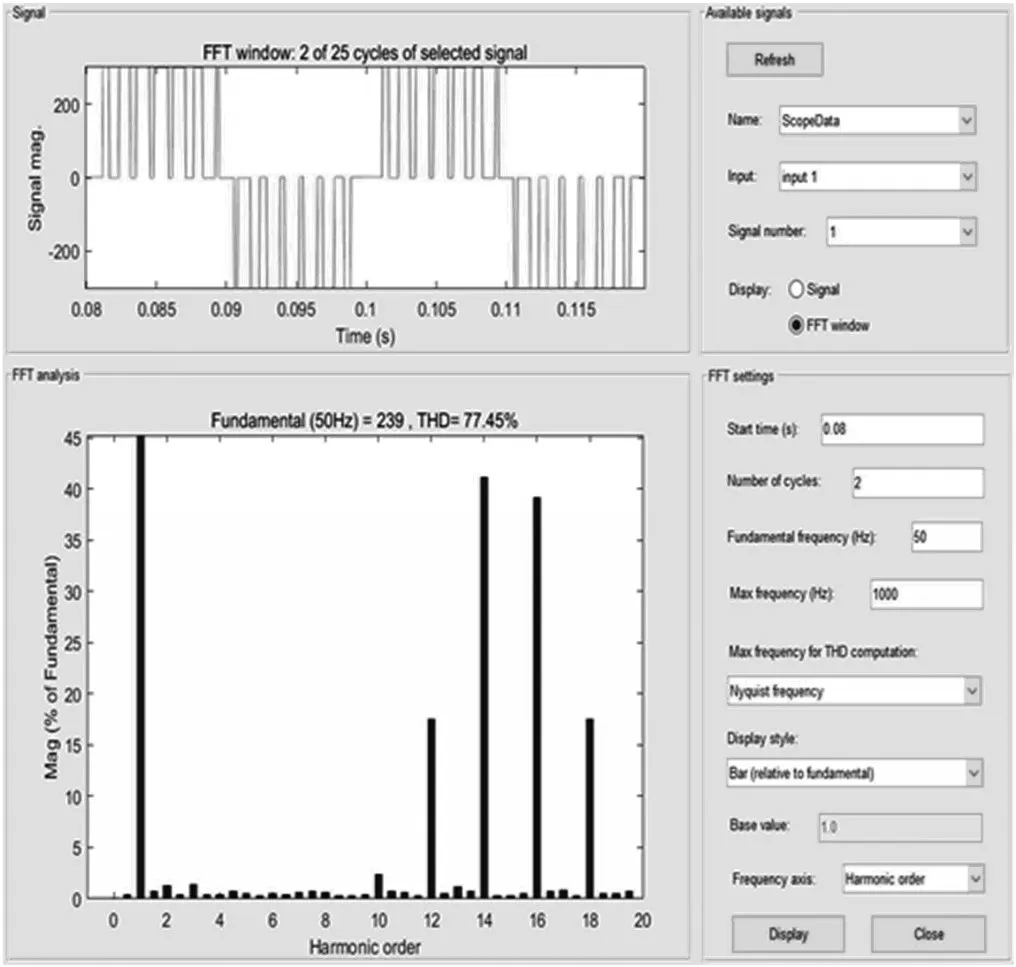
图9 M=0.8，P=15 时单极性逆变电路输出电压的FFT 分析结果

由图9 可知，基波幅值增加到239 V，不过仍与理论值相近。输出电压中依然不含开关次整数倍谐波，但第12 次谐波有所增加，为基波的17.49%，第14 和16 次谐波有所降低，分别为基波的41.15%和39.18%，最终总谐波失真降为77.45%。

将调制度设为0.8，载波比设为20，得到的输出电压的FFT 分析结果如图10 所示。

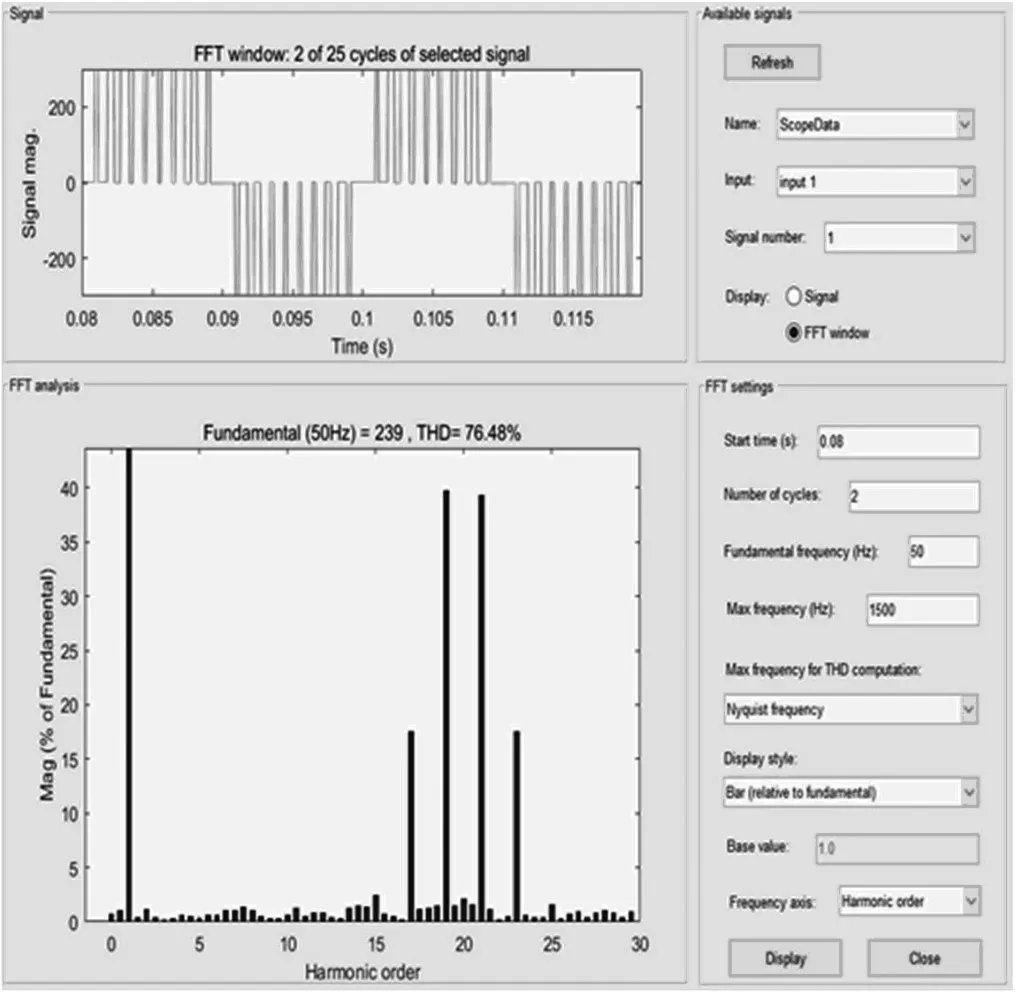
图10 M=0.8，P=20 时单极性逆变电路输出电压的FFT 分析结果

由图10 可知，基波幅值保持不变，输出电压中开关次整数倍谐波依然被消除，不含第20 次谐波，第19 和21 次谐波分别为基波的39.69%和39.34%，而最低次谐波增加到第17 次，但总谐波失真持续降为76.48%。

通过以上仿真结果可知，SPWM 逆变器的谐波特性与调制度、载波比这两个重要参数密切相关。当载波比不变，调制度越大时，总谐波失真就越小，则输入波形的失真程度也越小；当调制度不变，载波比越大时，最低次谐波离基波便越远，总谐波失真也相对减小。由此得出，合理增大调制度和载波比可以减少输出电压的谐波成分，从而有效改善输出电压的质量。

3 结 论

本文基于电压型SPWM 逆变电路，分别对双极性和单极性两种调制方式进行建模仿真，并对比两者的谐波特性，发现在线性调制情况下单极性调制的谐波性能更好。其次针对重要参数调制度和载波比，进一步分析两者对单极性逆变电路谐波成分的影响，仿真结果验证了模型的正确性，并证明该模型具有方便、灵活、直观等特点。此电路仿真模型虽然简单，但在软件中能够采取多种方式实现，后续可根据实际情况对相关元件及参数进行优化，设计出最佳的谐波抑制方案。