翼伞后缘偏转过程的流固耦合动力学特性
2023-06-16高兴龙张青斌李志辉
高兴龙,陈 钦,*,张青斌,李志辉
(1. 中国空气动力研究与发展中心,绵阳 621000;2. 国防科技大学 空天科学学院,长沙 410073)
0 引 言
翼伞是一种双层结构的柔性矩形翼,上、下翼面用翼型的肋幅分隔成若干气室,翼型前缘开口,在前进飞行中形成“冲压空气”,维持若干个气室的内压以保持翼型[1]。当翼伞系统需要进行机动转弯和雀降等操纵动作时,会对翼型后缘进行下拉偏转操作来实现。
翼伞后缘偏转的操纵过程会显著改变翼面的整体气动布局,同时需要多根操纵绳精确协同控制,是典型的气动与结构紧耦合问题,涉及到的动力学问题复杂多变。对于翼伞系统操纵过程的动力学机理问题研究一直是降落伞领域的关键技术和热点问题。著名的美国X-38 太空成员返回飞行器利用翼伞后缘下偏进行减速着陆的操纵,成功实现了太空人员返回安全着陆,是迄今为止世界上最大最先进的翼伞研究项目[2]。除此之外,比较典型的应用案例有美国研制的联合精确空投系统(joint precision airdrop system,JPADS),该系统是一个高空、全天候、GPS 制导的精确空投系统,包括超轻型和轻型两种布局,前后两者的最大载重量分别约为998 kg 和4536 kg,空投精度优于50~100 m。其他案例还有加拿大的“雪雁”(SnowGoose)侦察系统和“夏尔巴人”(Sherpa)精确空投系统、欧洲的SLG-Sys 自主滑翔伞降系统等[2]。
目前对于翼伞后缘偏转的动力学行为研究主要依靠数值仿真和试验,其中数值仿真主要采用流固耦合仿真技术对冲压翼伞动力学行为进行预测。目前国内外专门针对翼伞流固耦合过程的动力学机理研究已经逐渐由传统的完全试验法、半试验半理论法和完全理论法三种手段,转向了基于先进CFD 和CSD 方法的大规模并行数值仿真技术。Tang 等[3]基于LS-DYNA 软件中的ICFD 流体求解器和结构求解器仿真计算了翼伞后缘下偏过程的结构变形行为。Tezduyar 所领导的团队基于DSD/SST 有限元方法开展了冲压翼伞系统的流固耦合计算仿真[4]。Fogell等[5]基于松耦合、利用CFD 和CSD 方法对翼伞稳态飞行的充气外形进行流固耦合仿真,研究了翼伞结构变形和周围的流场特性。Altmann[6]使用势流理论和简化有限元法分析了翼伞的流固耦合问题。近年来,国内专门针对翼伞系统的流固耦合研究也逐渐增多,Nie 和Cao[7]基于Dirchlet/Neumann 迭代方法研究了翼伞充气过程的流固耦合问题,腾海山团队[8,9]基于LS-DYNA 求解器对翼伞稳态构型进行了流固耦合仿真,同时对大型翼伞操纵转弯过程的气动特性进行仿真分析。汪龙芳等[10]基于索膜有限元模型和CFD 方法对翼伞稳态飞行的气动变形进行了三维数值模拟,并分析了气室的“鼓包”现象。孙青林等[11-12]研究了襟翼偏转过程翼伞系统的气动性能变化。郭一鸣等[13]基于松耦合方法和参数辨识开展了翼伞变形和下偏情况的动力学和气动性能仿真。但是针对翼伞后缘下偏过程的气动与结构耦合动力学特性研究较少,本文分别考虑翼伞后缘偏转过程的非线性气动特性和结构响应行为,采用数值仿真与试验对比的方法深入分析了翼伞单侧和双侧后缘偏转过程的流固耦合动力学特性。
本文基于Structured ALE(S-ALE)流固耦合方法对翼伞后缘偏转过程进行动力学建模和仿真分析。研究翼伞三维模型后缘偏转过程、伞衣结构场和周围流场的时变演化规律及分布特性,为进一步指导大型翼伞精确空投系统的飞控系统设计和技术应用提供参考。
1 流固耦合建模
1.1 问题描述及假设
本文所研究的翼伞后缘偏转过程是针对充满鼓包状态的翼伞三维模型进行的。翼伞系统包括伞衣、伞绳和挂重载荷,几何模型如图1 所示。实际流固耦合仿真过程只考虑伞衣结构与流场的双向耦合作用;伞绳在翼伞偏转过程承受拉力,且通过伞绳施加后缘下拉过程的作用力载荷;忽略伞绳与周围流体的耦合作用和绳索的阻尼效应。
1.2 结构动力学
翼伞伞衣为柔性织物结构,一般由透气量极低的抗撕锦丝绸材料制成,本文忽略伞衣织物结构的透气量,则结构域的控制方程可以表示为[14]:
其中,ρs为材料密度,u为结构质点的速度矢量,σs为柯氏应力张量,fs为作用在结构的外部力, Ωs代表结构域的速度边界。
1.3 流体动力学
翼伞系统周围流体域的动力学方程为[15]:
其中,ρf、uf分别为密度和速度矢量,ff和 σf分别为外部力和应力张量, Ωf代表流体域的速度边界。通过引入ALE 格式,网格可以自由移动。在参考构型下不可压缩流的ALE 格式控制方程为:
其中,流体速度uf=v-w,v和w分别为参考构型下的流体质点速度和材料网格点速度,g是单位密度的外力矢量。 当v=w时,公式为拉格朗日形式;当v≠w时,公式为欧拉格式。同时给出Dirichlet 和Neuman形式的边界条件如下:
其中,n是法向矢量,h为流固耦合边界接触力矢量。
1.4 罚函数法
在翼伞系统的整个后缘偏转过程中,伞衣结构变形与周围流场变化相互作用,通过流固耦合界面信息的传递保证相互作用过程的能量守恒。通常有限元模型很难实现流体和结构网格的完全匹配,本文基于欧拉-拉格朗日描述下的罚函数法进行流体与伞衣结构间节点力信息的传递,该方法允许非匹配的流体和结构网格[16]。
流固耦合界面为伞衣织物结构表面,罚函数的穿透力fc计算公式为:
其中,ks代表罚函数的刚度系数;m为积分时间步;dm代表结构节点在第m个时间步进入流体域的穿透深度,与结构和流场网格节点的相对运动速度有关,可以在积分过程进行迭代计算。
利用穿透深度和相对运动速度可以在每个时间步内判断穿透是否发生,若穿透发生则在流固耦合界面上对流场和结构网格节点施加大小相等、方向相反的作用力,以满足流固耦合界面的受力平衡:
假设流体为渗透性介质,采用显式动力学积分方法对仿真模型进行迭代计算,从而完成流固耦合信息的关联和传递。
2 仿真方法验证
首先针对翼伞气室单元后缘偏转过程进行仿真计算,初步验证本文所采用方法的计算收敛性和可行性。建立翼伞气室结构的三维有限元模型,并在后缘沿操纵绳方向施加下拉载荷。流场域完全包裹结构模型,流场网格采用结构化网格。为避免因流体和结构单元之间尺寸差异过大而导致显式动力学积分过程可能出现的非物理特征“沙漏现象”,进而引起计算发散,流场网格尺寸与结构网格尺寸尽量接近1∶1,如图2 所示。

图2 翼伞气室流固耦合仿真网格模型Fig. 2 Mesh model of the parafoil cell for the FSI simulation
本文采用S-ALE 求解方法对流固耦合模型进行仿真计算,S-ALE 方法与传统ALE 方法的基本理论相同,均包括了映射过程的对流输运、界面重构和欧拉流场与拉格朗日结构相互作用的流固耦合过程[17]。不同的是,在网格的处理方法上,S-ALE 方法采用自动生成网格技术,即流场网格根据控制点设定的方向、增长率、网格尺寸、网格密度等参数在仿真过程中随着时间步的推进逐渐产生,仿真前无需单独建立流场网格。这可以极大减小网格处理时间并提高计算效率。经过仿真测算,与传统ALE 方法相比,S-ALE 方法的计算效率可以提高60%[18]。
计算的来流速度为15 m/s,来流攻角为0°,流场和结构域的计算结果如图3~图5 所示。
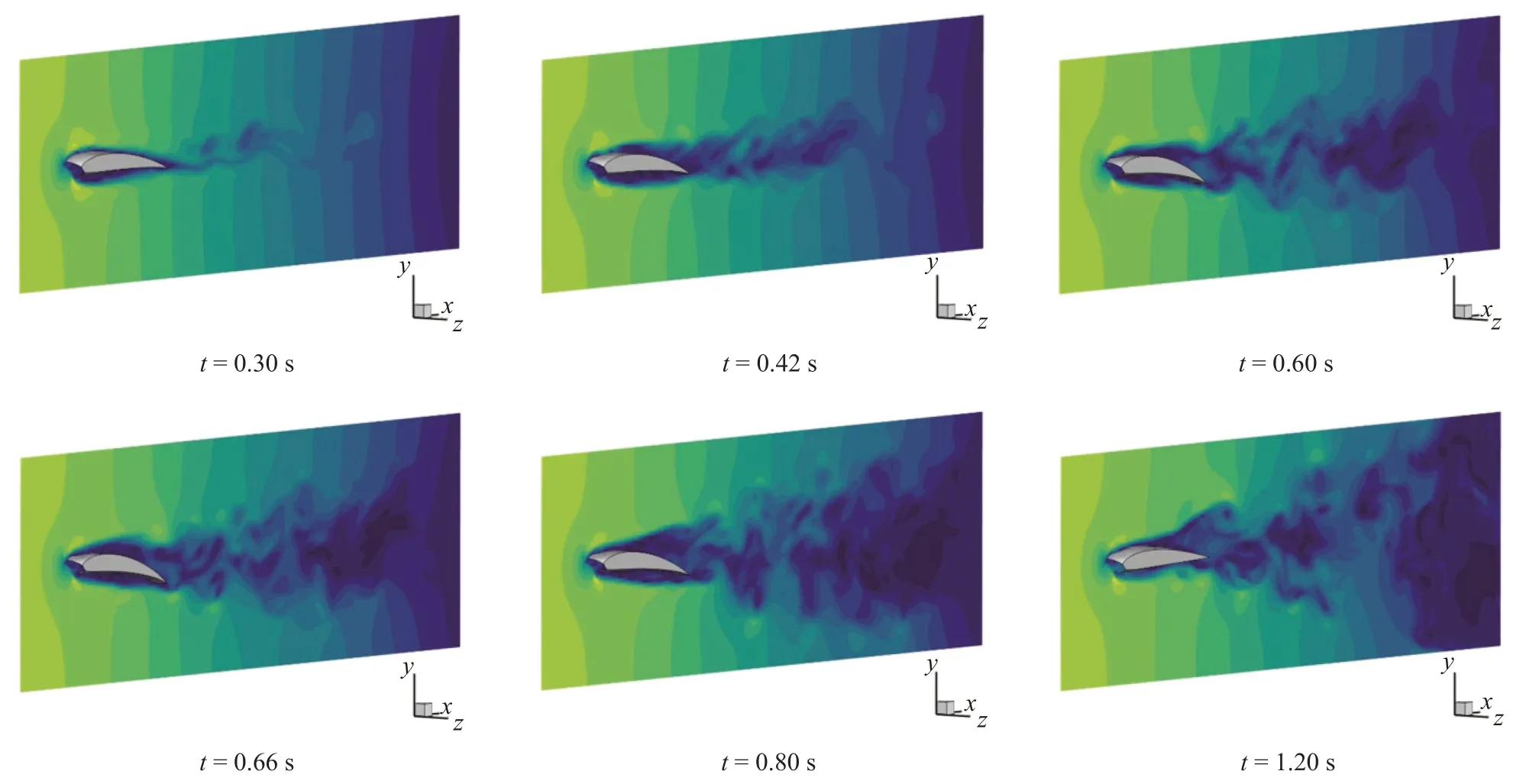
图3 翼伞气室后缘偏转过程流场速度变化云图Fig. 3 Velocity contour variations of the parafoil cell under trailing-edge deflection
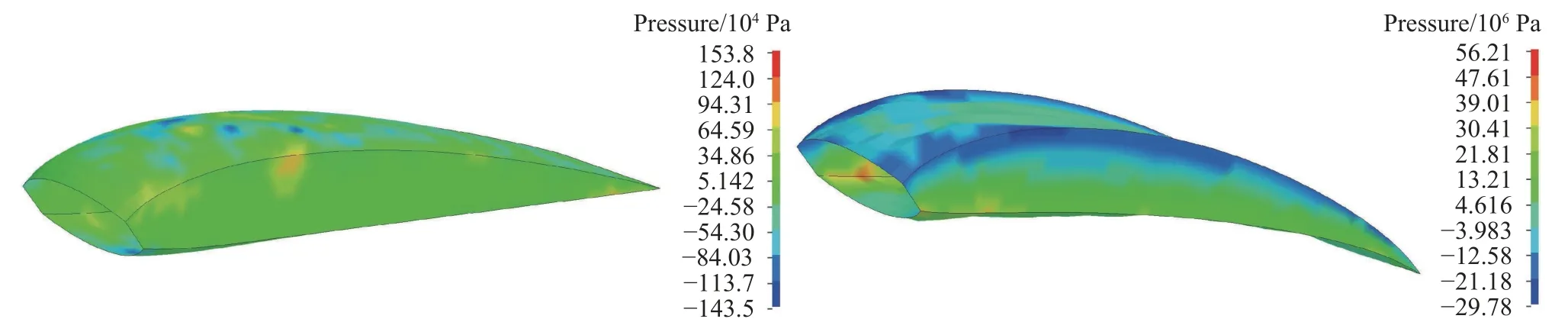
图5 翼伞气室后缘偏转过程伞衣表面压力分布云图Fig. 5 Pressure contours of the parafoil cell under trailing-edge deflection
从图3 流场演化结果中的速度云图可以明显看到涡流由上翼面向后缘逐渐过渡和破碎的过程。随着后缘向下偏转程度的增大,在后缘尾部的上端出现明显的低速区域,形成高压的逆压梯度,从而引起流动分离现象。从图4 和图5 的伞衣结构应力和压力分布云图中可以看出,气室中间鼓包区域为受力较为集中且强度高的区域。
将采用本文流固耦合方法仿真计算得到的下偏状态翼伞气室单元结构有限元模型导出,作为几何边界模型,采用Fluent 对该导出的后缘偏转气室单元进行气动特性仿真计算验证,来流速度同样取为15 m/s,湍流模型选择标准k-ω模型,计算得到的翼伞气室单元后缘下偏状态翼型表面的压力系数为0.65。采用本文流固耦合仿真方法计算得到的同样状态翼型表面压力系数为0.62。两种方法的结果较为接近,初步验证了本文方法的有效性和可靠性。
3 仿真结果与验证
翼伞气室单元仿真计算初步验证了本文方法的可行性和收敛性,将本文方法进一步应用于整个翼伞系统多气室后缘偏转过程的流固耦合仿真。为了模拟翼伞机动转弯和雀降着陆两个经典操纵动作,分别对整个翼伞系统模型的后缘单侧下偏和双侧下偏过程进行仿真计算。
3.1 流固耦合结果
图6 和图7 为翼伞后缘单侧和双侧下偏操纵过程的伞衣表面结构Von Mises 应力分布云图。从图中可以明显看出伞衣的上翼面整体应力分布较为均匀,但当后缘下偏时,在偏转与未偏转的转折交接区域会出面明显的应力集中且受力增大;同时翼型前缘也相应出现类似现象,且与后缘应力集中区域的受力水平接近。说明翼伞后缘偏转发生的转折交接区域和偏转侧前缘切口区域是在翼伞操纵过程比较容易发生撕裂现象的区域,应考虑在这两处增加结构强度。从伞衣结构受力水平来讲,在下偏量相同的情况下,双侧下偏的伞衣结构受力明显高于单侧下偏情况。
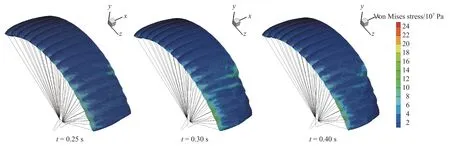
图6 不同时刻单侧下偏伞衣表面结构Von Mises 应力云图Fig. 6 Von Mises stress contours of the canopy under single deflection at different time instances
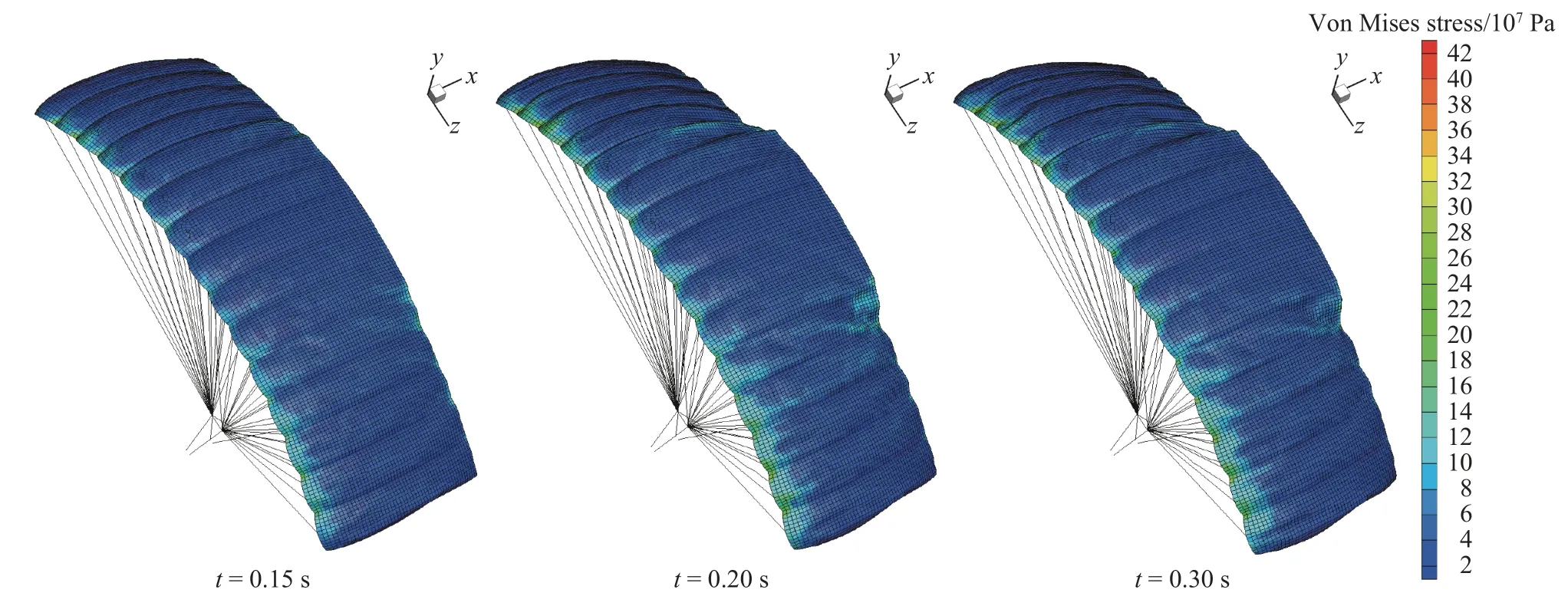
图7 不同时刻双侧下偏伞衣表面结构Von Mises 应力云图Fig. 7 Von Mises stress contours of the canopy under double deflection at different time instances
图8 和图9 为翼伞后缘双侧下偏过程不同时刻的伞衣周围流场速度变化云图。从单侧下偏过程的速度变化分布云图可以看出,在翼伞的尾缘顶部紧贴上翼面附近出现近似圆形的高速区域,当下偏时该区域被拉长,下偏完成后此区域减小。该高速区域会使上翼面顶部的气流自后缘向前缘倒流,产生流动分离,这也是翼伞转弯操纵出现失稳现象的主要原因。从双侧下偏过程的横向剖面流场速度分布云图可以看出,该高速区域主要存在于翼伞下偏发生的转折交界区域附近。
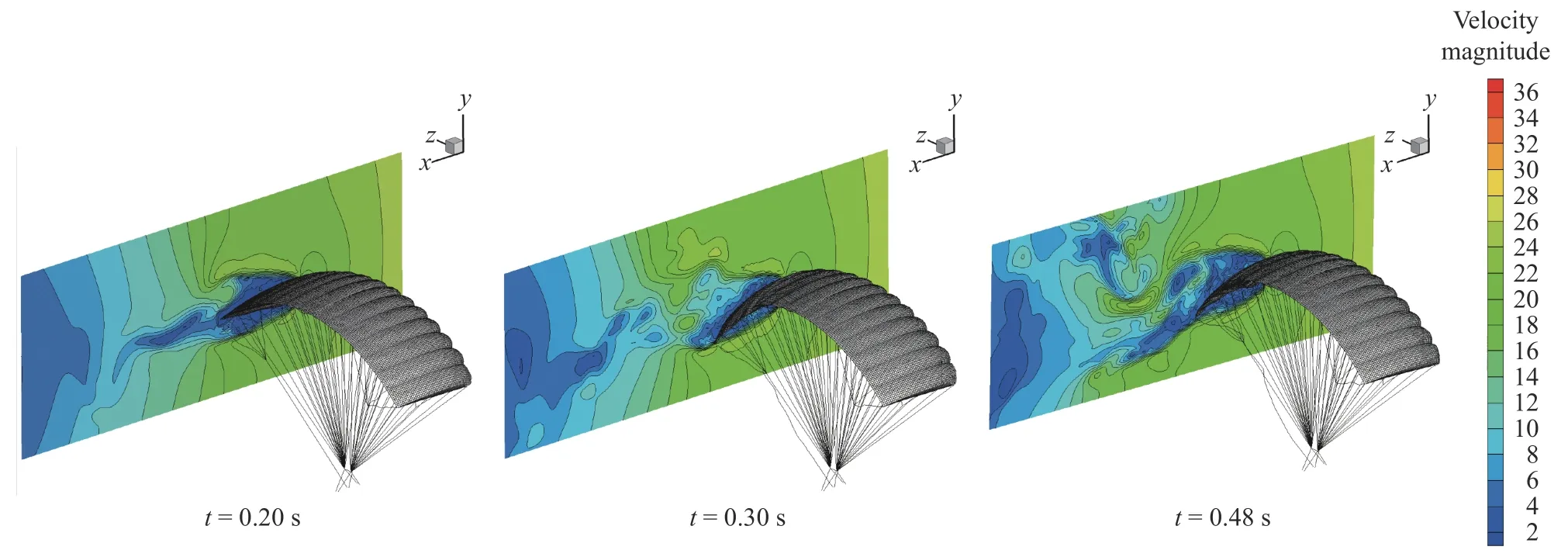
图8 不同时刻单侧下偏伞衣周围流场速度变化云图Fig. 8 Velocity contours around the canopy under single deflection at different time instances

图9 不同时刻双侧下偏过程周围流场速度变化云图Fig. 9 Velocity contours around the canopy under double deflection at different time instances
3.2 性能曲线结果
图10 为翼伞后缘单侧和双侧下偏过程所施加的下偏量随时间的变化曲线。两种情况的下偏量相同。图11~图13 分别为两种情况的翼伞气动阻力面积、升力系数、阻力系数三者随时间变化曲线。后缘单侧下偏对应翼伞的操纵转弯动作,下拉量开始时间为0.2 s,此时升力系数出现一个峰值,下偏量达到最大的时刻为0.3 s,此时阻力系数最大,阻力面积的变化与下偏量变化结果趋势较为一致。
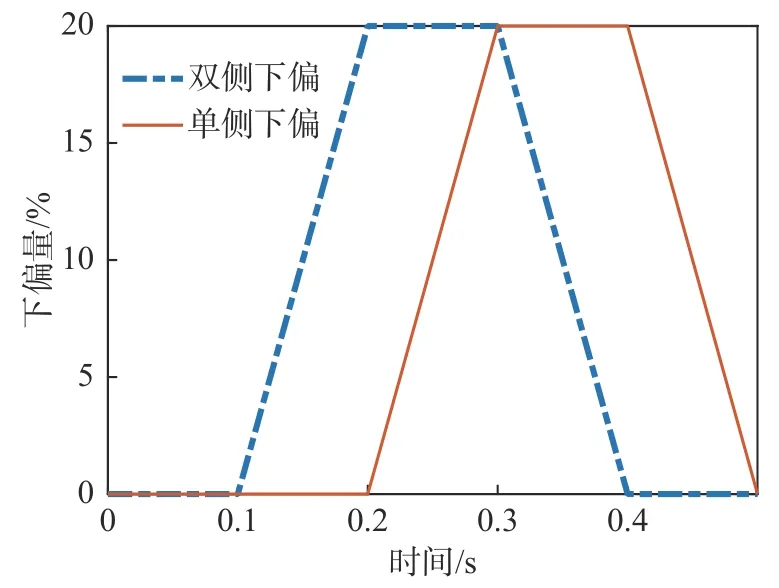
图10 翼伞后缘下偏过程下偏量随时间变化Fig. 10 Time variation of the deflection for the parafoil under trailing-edge deflection
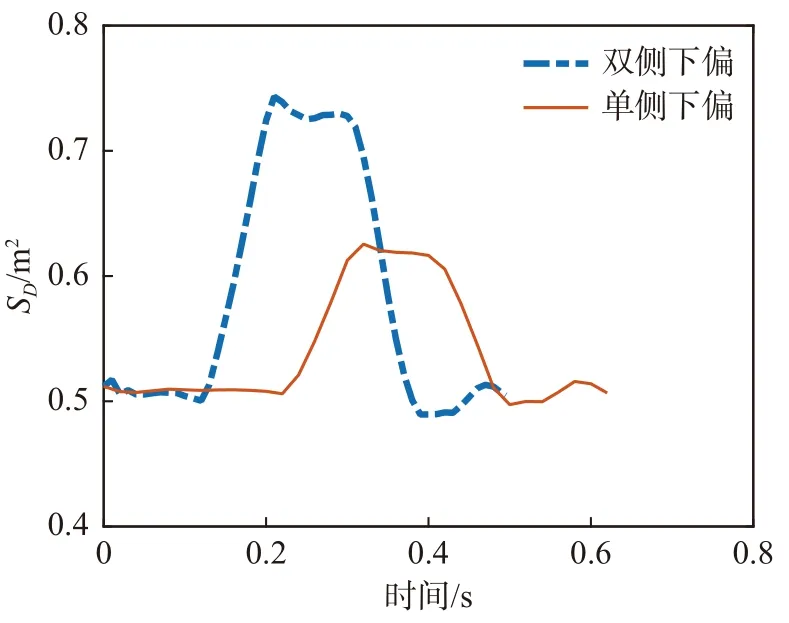
图11 翼伞后缘下偏过程气动阻力面积随时间变化Fig. 11 Time variation of the drag area for the parafoil under trailing-edge deflection

图12 翼伞后缘下偏过程气动升力系数随时间变化Fig. 12 Time variation of the lift coefficient of the parafoil under trailing-edge deflection
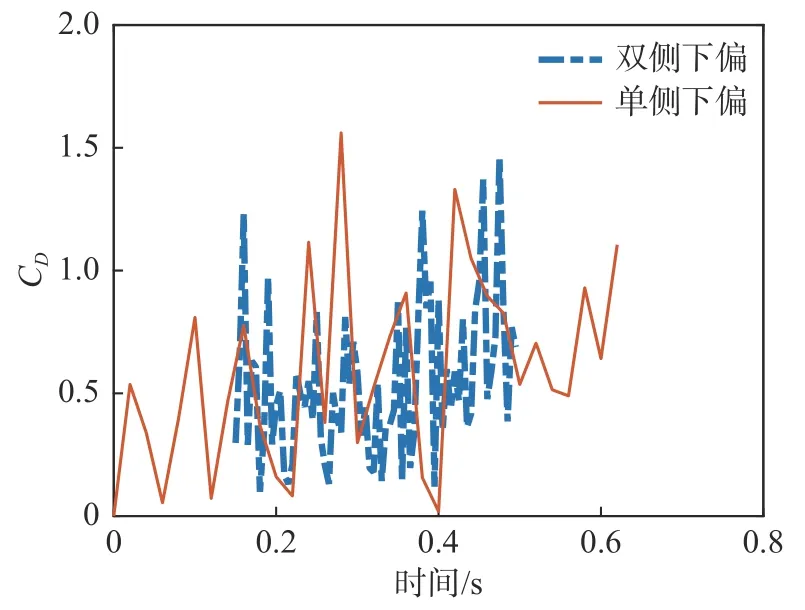
图13 翼伞后缘下偏过程气动阻力系数随时间变化Fig. 13 Time variation of the drag coefficient of the parafoil under trailing-edge deflection
双侧下偏过程对应翼伞的雀降着陆操纵动作,翼伞下偏量达到最大的时刻为0.2 s,但翼伞最大阻力系数出现的时间约为0.44 s,最大升力系数出现的时间约为0.38 s,均晚于下拉操纵量达到最大的时刻,表明冲压翼伞后缘双侧下偏操纵过程具有延迟响应的特性。
3.3 试验验证
为进一步验证本文仿真结果,将流固耦合仿真计算获得的后缘双侧下偏过程达到不同下偏量的翼伞系统结构有限元模型输出保存,利用ANSYS 软件将有限元模型转换为翼伞结构外轮廓的实体几何模型,并采用3D 打印技术打印出实体模型。
在0.55 m×0.4 m 低噪声航空声学风洞对翼伞模型进行静态测压吹风试验,风速同样为15 m/s。在翼伞每个气室的翼型模型中剖面布置一定数量的测压孔,对测得的压力分布在升力方向积分,得到该状态翼伞系统的升力系数。
表1 为翼伞后缘偏转模型升力系数仿真与试验的对比结果,其中仿真结果为利用本文方法对不同下偏量的翼伞结构外轮廓模型进行的流固耦合仿真。从对比可以看出仿真结果与试验结果较为一致,且不同下偏量对应的升力系数变化趋势相同。

表1 翼伞后缘偏转模型升力系数对比结果Table 1 Lift coefficient comparison of the parafoil under trailing-edge deflection
4 结 论
本文研究了翼伞后缘下偏过程的流固耦合动力学问题。在单个气室翼型的后缘偏转过程仿真研究中发现偏转过程气室周围流场出现分离流动现象。之后对整个翼伞的后缘下偏过程进行流固耦合仿真,并利用风洞试验对仿真结果进行验证,研究结果表明基于S-ALE 和罚函数法的流固耦合技术可以进行翼伞后缘偏转过程的流固耦合动力学行为研究:1)伞衣结构计算结果表明后缘下偏过程应力集中区域位于翼型前缘切口和后缘下偏转折发生区域;2)通过分析气动参数的时间历程演化趋势,发现冲压翼伞的后缘下偏过程会出现明显的延迟响应现象。总之,利用本文所采用的流固耦合方法可以对翼伞空投系统的气动结构耦合动力学行为进行较好的预测,有助于翼伞精确空投系统的技术验证和设计分析。
