基于数值模拟的飞机近场尾涡特征参数计算
2023-06-16温瑞英李鹏柯王红勇
温瑞英,李鹏柯,刘 聪,王红勇
(中国民航大学 空中交通管理学院,天津 300300)
0 引 言
尾流是飞行过程中飞机上下翼面压力差导致气流从机翼后缘脱落形成的一对反向旋转的尾涡,有空间尺度大、旋转切向速度高、持续时间久等特点。尾涡流场的存在会影响后续飞机的飞行姿态,甚至引发飞行事故,国际民航组织制定了尾流间隔标准来预防尾流造成的飞行事故。随着航空工业的发展,航班流量不断增加,机场容量的提升成为航空运输发展中迫切需要解决的问题。但尾流间隔过大将限制机场容量增加,因此建立尾流间隔预测系统,合理地缩减尾流间隔是提高机场容量、缓解航空压力的关键。在这样的现实背景下,对飞机尾流的研究在近年来得到了不断发展和完善。
基于计算流体动力学的数值模拟方法是研究飞机尾流的主要手段之一[1]。尾涡在机翼后缘的延伸距离长达十几公里,在计算条件限制下使用数值模拟方法对尾流的研究主要分为近场和远场两方面。
在近场方面,国内外研究者采用不同的数值模拟方法对翼尖涡的形成及尾涡近场演变进行了大量研究。Chow 等[2]基于雷诺平均N-S 法(RANS)模拟了NACA0012 机翼翼尖涡的形成和近场演化过程,发现翼尖涡近场卷起为湍流运动,且强度随流向距离迅速衰减。Morton 等[3]基于RANS 和分离涡法(DES)对三角翼的近场尾涡进行研究,发现大迎角条件下DES 模拟结果与实验数据更拟合。Jiang 等[4]基于大涡模拟(LES)研究近场尾涡的形成过程,分析了翼尖涡脱落转变为稳定近场尾流的原因。刘薇等[5]基于RANS 对 NACA0012 机翼近场尾涡进行模拟,发现在采用六面体网格的数值模拟中,RKE 模型得到的结果与风洞实验值更吻合。温瑞英等[6]基于RANS 对B757-200 飞机的近场尾涡特性进行数值模拟,研究了飞机近场尾涡的演化特征。艾国远等[7]基于LES研究不同雷诺数对翼尖涡的层流分离流动机制的影响。林孟达等[8]基于LES 研究飞机尾涡在大气中的演变特性,对尾涡近场卷起过程采用升力面尾涡生成法,结果表明该方法可减少网格量,提高计算效率。
在远场方面,国内外研究者主要研究气象条件对尾涡消散的影响和尾涡的近地演化规律。Han 等[9]基于LES 研究了大气湍流与飞机尾流的关系,发现尾流的寿命会受到周围大气湍流的显著影响。Proctor 等[10]基于LES 对飞机尾流的地面效应进行研究,发现尾涡在距地面高度低于0.6 倍初始涡间距时,其强度受到地面效应的影响而急剧下降。Stephan等[11]基于LES 研究地面加设障碍物对飞机尾流的影响,发现合理地布置地面障碍物可以加快尾涡的消散。Xu 等[12]基于LES 研究了跑道设置吹气或吸气区对尾流消散的影响,结果发现吹气区附近产生的分离涡对尾流的消散有着明显的影响。魏志强等[13]基于RANS 方法对尾涡在侧风条件下的演化进行了研究,发现水平方向上高强度的侧风能加速尾涡的消散。上述研究均采用简化尾涡速度模型对近场尾涡进行初始化,该方法在一定程度上忽略了近场尾涡对尾涡后续演化及其衰减的影响。
目前关于模拟飞机尾涡完整生命周期的研究较少,对尾涡近场和远场的独立研究无法准确地展示尾涡的整体演化规律。由于尾涡的生命周期长,因此可采用近远场耦合的多段法进行全流场尾涡数值模拟,在保证计算结果高精度的同时,避免计算量和计算条件的限制。本文基于尾流数值模拟现状,对A320 飞机的近场尾涡进行了数值计算,研究了飞机近场尾涡特征参数的计算方式,并利用Hallock-Burnham(H-B)和Lamb-Oseen(L-O)模型对尾涡流场进行反演,验证了尾涡特征参数计算方法的有效性。基于飞机近场尾涡所提取的特征参数可以作为远场尾涡演化和消散机制研究的基础。
1 飞机尾涡数值模拟方法
1.1 几何模型与网格划分
本文采用A320 飞机的机翼作为计算模型,具体的计算外形和网格分布图如图1 所示,模型具体尺寸见表1。

表1 A320 机翼数据Table 1 Wing parameters of A320
三维机翼模型的坐标原点取机翼最前缘点,气流流动方向为z轴负方向,沿展向指向左翼为x轴正方向,机翼面上方垂直于气流流动的方向为y轴正方向。
计算区域设置为:机翼上方取3cr,机翼下方取5cr,机翼左右侧各取3cr,机翼前方取4cr,机翼后方取25cr。
为了获得较高的网格精度和质量,计算网格采用结构化六面体网格。为了提高网格的正交性,机翼周围的网格采用自适应O 型网格进行划分。经过反复试算与调整,综合考虑计算需求和计算配置,最终计算域网格分布为Nx×Ny×Nz= 270 × 120 × 420,总网格数为1.4018×107。
1.2 数值模拟方法与边界条件
1.2.1 数值模拟方法
本文计算在天河1 号超级计算机上完成。采用RANS 方法捕捉飞机尾涡的形成并逐渐卷起的过程,利用有限体积法进行求解。雷诺平均法求解的雷诺方程如下:
式中: 〈〉为系综平均,ui表示雷诺平均速度分量,xi和xj(i,j= 1, 2, 3) 表示三个方向的坐标,υ为运动黏度,p为压强,fi为质量力,ρ为流体密度。
1.2.2 边界条件设置
计算域的翼展方向、飞行方向、顶部和底部的边界均设为压力远场,飞机机翼表面设为无滑移壁面。
根据A320 型飞机进场和离场速度,来流速度为67 m/s,飞行马赫数为0.2,飞行迎角为10°,大气压力为104103.1 Pa。
2 飞机尾涡特征参数计算方法
尾涡的寿命一般分为近场涡与远场涡两个阶段,其中,近场涡可分为卷起区和成熟区两部分,远场涡可分为中远场和消散区两部分[14],尾涡寿命阶段分布如图2 所示。

图2 尾涡寿命各阶段示意图Fig. 2 Temporal evolution of wake vortices
一般认为沿机翼后缘延伸10 倍翼展长度内的区域为近场涡区域。其中,从机翼后缘脱落的涡面卷起形成高度集中的涡旋的过程为卷起区,拥有成型涡核且涡柱稳定的阶段为成熟区。图3 通过三维轴向涡量等值线图展示了A320 机翼在7 个翼展内的近场尾涡演化过程,可以看出近场尾涡分为两个区域:1 倍翼展(−z/b= 1)内为卷起区,该区域内涡核刚开始成形;−z/b= 2~7 为成熟区,是尾涡逐渐稳定乃至成熟的过程。图4 为−z/b= 2 内的涡量等值线图,可以看出当尾涡流向距离为−z/b= 1 时涡核开始卷起。

图3 A320 飞机的近场尾涡Fig. 3 Near-field wake vortices of A320

图4 近场尾涡卷起过程Fig. 4 The lift up of near-field wake vortices
在描述飞机尾涡基本特性时,采用相对于基准参数的无量纲标称参数。本文采用以下两个基准参数简化计算,即初始尾涡环量Γ0和初始尾涡间距B0:
式中:ny为飞机的法向过载;W为飞机重量;ρ为飞行高度上的空气密度;V∞为飞机飞行速度;b为机翼的翼展。
2.1 涡核位置和涡核间距
飞机的尾涡可以简化成两个旋转方向相反的涡旋,涡旋中心存在一个涡核。涡量是描述尾涡运动的一个矢量[15],本文通过寻找涡量最大值的方法来确定涡核的位置,其中涡量ω的表达式见式(4):
式中:ωx=∂w/∂y−∂v/∂z为x轴涡量分量,ωy=∂u/∂z−∂w/∂x为y轴涡量分量,ωz=∂v/∂x−∂u/∂y为z轴涡量分量,u、v和w分别为沿x、y和z方向的速度分量。
通过最大涡量值确定左右涡核位置后,两涡核之间的距离即涡核间距B。
2.2 涡核半径
尾涡的旋转特性可以用切向速度来描述。尾涡的切向速度Vθ计算公式如下:
z轴方向速度分量相对于x轴和y轴方向的数值较小,因此在切向速度的计算中忽略不计。
涡核半径为涡核位置与最大切向速度位置之间的长度[6,16,17],文献中仅考虑切向速度最大的点,这种由单个值计算的涡核半径存在一定偏差,因此本文采用平均值的方法来计算涡核半径。
2.2.1 平均正圆法
平均正圆法是以最大切向速度值划分出包含多个点的速度范围,将多个点距离涡核位置的长度取平均值作为涡核半径,如图5 所示为左涡涡核计算示意图,具体方法为:
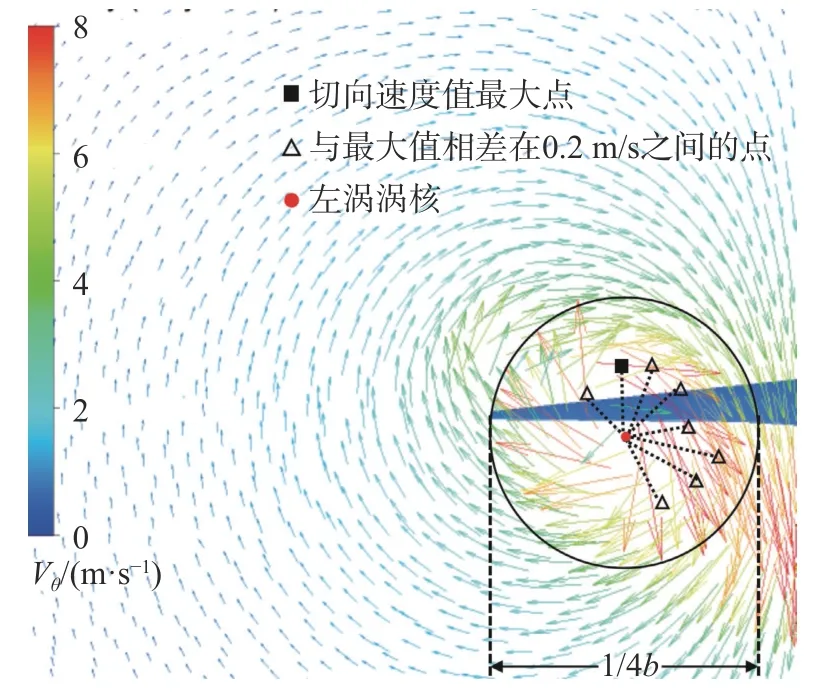
图5 平均正圆法计算涡核半径Fig. 5 The average circle method computing vortex radius
1)为避免右涡速度场对左涡的影响,以左涡核为原点,选取以涡核为圆心,半径不超过翼展四分之一的圆为计算域;
2)在计算域内找到切向速度值最大的点,并找到满足与最大切向速度值相差在0.2 m/s 内的所有点;
3)计算上述所有点与涡核之间的距离,将其平均值定义为涡核半径。
2.2.2 平均椭圆法
图6 给出了−z/b= 7 截面处左涡面的切向速度分布图,其涡核形状接近椭圆,因此本文提出如图7 所示的平均椭圆法来确定涡核半径,以左涡为例,具体方法为:

图6 −z /b = 7 截面尾涡切向速度矢量图Fig. 6 Tangential velocity of the wake vortex at −z /b = 7
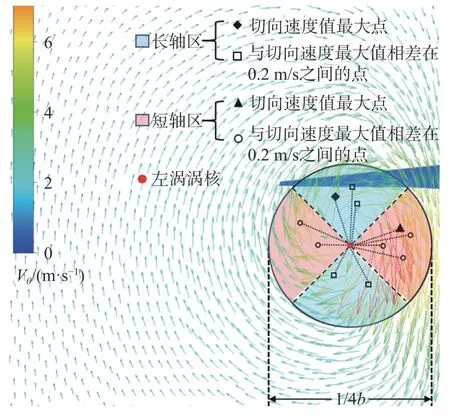
图7 平均椭圆法计算涡核半径Fig. 7 The average ellipse method computing vortex radius
1)以左涡核为原点,选取半径不超过翼展的四分之一的圆为计算域;
2)涡核的垂直方向定义为y轴,与y轴夹角为−45°~+45°、−135°~+135°之间的区域设为长轴区,在长轴区内找到切向速度最大的点,并找到满足与最大值相差0.2 m/s 的所有点,将其与涡核之间的距离平均值定义为长轴半径;
3)同理,将涡核的水平方向定义为x轴,与x轴夹角为−45°~+45°、 −135°~+135°之间的区域设为短轴区,与长轴做法相同得到短轴半径;
4)将长轴半径和短轴半径的平均值定义为涡核半径。
2.3 尾涡环量
尾涡强度一般用环量来表征,环量是流体速度沿一条封闭曲线路径的线积分。根据切向速度剖面计算尾涡环量,如式(6):
式中:Γ(r)为距涡核径向距离为r处的尾涡环量;Vθ(r)为距涡核径向距离为r处的切向速度。
由于尾涡剖面内各点切向速度不同,因此常用平均环量,即对一个半径区间内的环量取平均值来表示尾涡强度,计算公式见式(7):
式中,rl≤ri≤ru,rl为半径区间的下限,ru为半径区间的上限。
文献[18,19]通过激光雷达测量了飞机的尾涡数据,对尾涡环量的计算方法进行了评估。由于激光雷达不能捕获尾涡的细微结构,尤其是涡核附近的流场区域,因此文献[18,19]采用Γ5−15作为大型飞机(翼展约为60 m)尾涡强度计算的环量平均值,公式见式(8),式中半径间隔以1 m 为增量计算:
对于翼展为b的飞机模型,文献[19]给出计算尾涡环量的半径区间为b/12~b/4。
通过数值模拟可以得到尾涡整个流场的细微结构,本文通过分析中型客机A320 的近场尾涡环量随涡核径向距离的变化规律,探讨计算尾涡环量时更合适的半径区间。采用尾涡环量的平均绝对误差MAE 对半径区间选取的合理性进行评价,MAE 的计算见式(9):
图8 给出了A320 飞机−z/b= 2~7 的尾涡截面上左涡无量纲环量值Γ∗(Γ∗=Γ/Γ0)随涡核径向距离的变化规律。可知当涡核径向距离小于5 m 时,无量纲尾涡环量随径向距离的增加而急剧增大,在涡核径向距离5~11 m 之间,环量值随径向距离增加而缓慢增加,在11 m 处到达峰值后开始缓慢下降。

图8 无量纲尾涡环量随涡核径向距离的变化规律Fig. 8 The evolution of dimensionless circulation with the radial distance
1)半径区间下限rl的确定。此处采用固定半径上限、逐步增大半径下限的方式进行讨论,将b/2 向上取整作为半径区间的上限值,以1 m 为单位增大半径下限。图9 给出了MAE 值随半径下限值增大的变化规律,可以看出2 倍翼展截面的MAE 值最大,因为该截面上的尾涡刚卷起,速度特征不明显,而流向距离较远截面处的MAE 值较低。半径下限值小于3 m时,MAE 值随着下限值的增大而减小;半径下限值在4~10 m 之间时,MAE 值呈增大趋势;半径下限大于10 m 后,MAE 值开始减小。在半径下限取值为3 时MAE 值为极小值,因此半径下限的最优值为3 m,即rl= 3。

图9 MAE 值随半径下限值的变化规律Fig. 9 Variations of MAE with the lower bound of radius
2)区间上限ru的确定。将半径区间的下限rl=3 设为定值,对半径区间的上限进行讨论。为避免左右涡之间的相互干扰对尾涡环量计算精度的影响,以b/2 向上取整作为半径上限[16]。图10 反映了MAE值随半径上限值增大的变化规律。由图可知,在半径区间上限值小于10 m 时,MAE 值随半径上限值的增大而急剧减小;半径上限值在10~12 m 之间时MAE值缓慢减小;在半径上限值大于12 m 时,MAE 值基本保持不变。因此半径上限的最优值可取为12 m,即ru= 12。

图10 MAE 随半径上限值的变化规律Fig. 10 Variations of MAE with the upper bound of radius
结合图8 可知,涡核径向距离在3~12 m 之间时,环量值变化趋势平缓;低于3 m 时,环量值过低会使得MAE 值增大;高于12 m 时,环量值变化不明显,且由图10 可知增加了不必要的计算。综合可得,计算尾涡环量平均值的最佳半径区间可选为3~12 m。
图11 给出了不同半径区间尾涡平均环量的MAE 值随尾涡流向距离的变化规律。可以看出,Γ3−12得到的MAE 值低于Γ5−15和Γ3−9(根据b/12~b/4可得出A320 飞机计算尾涡环量平均值的半径区间为3~9 m)。因此基于数值模拟得出的近场尾涡,采用Γ3−12描述涡面环量分布更加准确。
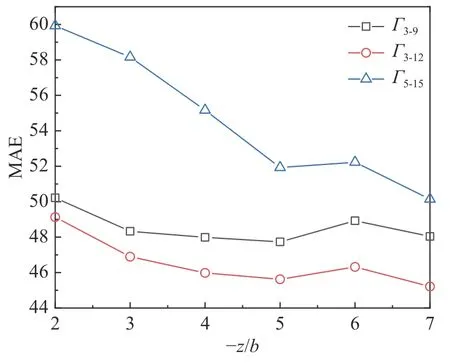
图11 不同半径区间MAE 值随流向距离的变化Fig. 11 Streamwise variations of MAE in different radius
2.4 尾涡特征参数计算方法验证分析
为了验证本文尾涡特征参数计算方法的精准度,采用H-B 和L-O 模型对尾涡流场进行验证,具体做法如下:
1)根据L-O 和H-B 的速度模型,推导出流场任意点处的速度计算公式,通过计算的涡核位置、尾涡环量和涡核半径得出一个反演速度场。
2)将反演速度场与数值模拟计算得到的尾涡速度场进行对比,对尾涡参数计算方法的准确性进行评估。
2.4.1 速度场的构建
假设尾涡流场中一个截面的左右涡核位置坐标分别为(x1,y1)和 (x2,y2),其中左涡涡核半径为rc1、环量为Γ1,右涡涡核半径为rc2、环量为Γ2。流场中任意一点的坐标为(x,y),该点距离左涡涡核的长度为r1,距离右涡涡核的长度为r2。图12 为两个点涡所计算的流场任意点(x,y)处展向和垂直方向上的速度分量。

图12 速度分量计算示意图Fig. 12 The calculation of velocity components
Hallock-Burnhan 模型简称H-B 模型,该模型的单点涡速度公式如式(10):
基于H-B 模型,计算流场任意点(x,y)处切向速度的展向速度分量Vx和垂直速度分量Vy,如式(11)、式(12):
Lamb-Oseen 模型简称L-O 模型。该模型的单点涡速度公式如式(13):
基于L-O 模型,计算流场任意点(x,y)处切向速度的展向速度分量Vx和垂直速度分量Vy,如式(14)、式(15):
2.4.2 速度场误差分析
为了反映反演速度场与数值模拟速度场之间的误差,本文选用均方根误差(RMSE)对结果进行评价,计算公式见式(16):
式中:Vxi、Vyi分别是反演速度场中任意一点的展向速度分量和垂直速度分量;ui、vi分别是数值模拟速度场中任意一点处的展向速度分量和垂直方向速度分量。
选取流向距离-z/cr=3.5、4、4.5、5、8、10、13、16、19、21、25,共11 个截面进行计算分析。
图13 为采用平均正圆法和平均椭圆法计算涡核半径时,速度场RMSE 值随流向距离的变化规律,其中选取3~12 m 的环量平均值作为尾涡环量。由图可知:当流向距离在−z/cr= 3.5~10 之间,两种计算方法得到的RMSE 值基本一致,且RMSE 值随着流向距离增加而急剧减小;当流向距离在−z/cr= 10~25之间,各方法得到的RMSE 值随流向距离增加而缓慢减小,且平均椭圆法的RMSE 值更低。说明采取平均椭圆法计算涡核半径更加精确。

图13 不同涡核半径计算方法下RMSE 随流向距离的变化Fig. 13 Streamwise variations of RMSE obtained by different methods of computing rc
图14 为采用不同半径区间计算环量平均值时,RMSE 值随流向距离的变化规律,其中涡核半径的计算方法为平均椭圆法。由图可知: RMSE 值随流向距离的增大而减小;对比三种半径区间,Γ3−12得到的RMSE 值最小。说明采用Γ3−12作为近场尾涡环量平均值更加精确。

图14 不同半径区间下RMSE 随流向距离的变化Fig. 14 Streamwise variations of RMSE at different radius intervals
由图13、图14 可知,整个近场中,在不同半径区间和不同涡核半径计算方法下,L-O 模型的RMSE 值均低于H-B 模型。因此,采用L-O 模型描述近场尾涡的速度分布时,拟合度更高。
3 飞机近场尾涡计算结果及分析
1)涡核位置。图15 为涡核位置所在的横向坐标随流向距离的变化规律。可以看出:在流向距离−z/cr= 5,即一倍翼展之后,左右涡核位置的横向坐标随着流向距离的增加而逐渐减小。

图15 涡核横向坐标随流向距离的变化Fig. 15 Streamwise variations of the lateral coordinates of vortex cores
图16 为涡核位置的纵向坐标随流向距离的变化规律。可以看出:左右涡的变化曲线重合,即下落趋势一致。随着尾涡流向距离的增加,左右涡核在流向距离−z/cr= 5 之后开始逐渐向下移动。

图16 涡核纵向坐标随流向距离的变化规律Fig. 16 Streamwise variations of the vertical coordinates of vortex cores

图17 无量纲涡核间距随流向距离的变化规律Fig. 17 Streamwise variation of the dimensionless distance between vortex cores
3)涡核半径。图18 为无量纲化左涡涡核半径随流向距离的变化规律。可以看出:在流向距离小于−z/cr= 10 时,涡核半径随着流向距离的增加而增加;流向距离在−z/cr= 10~16 之间,涡核半径小幅度减小;流向距离在−z/cr= 16 之后,涡核半径随着流向距离的增加而急剧增大。在近场尾涡区域,使用平均椭圆法计算得到的涡核半径值小于平均正圆法。
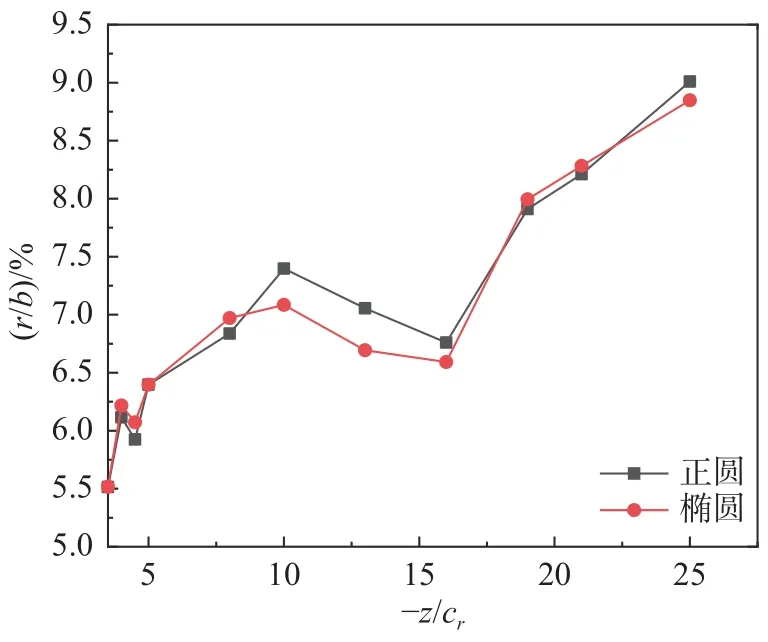
图18 无量纲左涡核半径随流向距离的变化规律Fig. 18 Streamwise variation of the dimensionless radius of the left vortex core
4 结 论
本文基于RANS 数值模拟方法,模拟了A320 机翼的近场尾涡演化过程,对其近场尾涡流场特征参数的计算方法进行了分析,主要结论如下:
1)对于数值模拟的A320 近场尾涡,采用平均椭圆法计算涡核半径,精度更高;作为特征参数进行尾涡速度场构建,拟合度更好。
2)通过对比尾涡截面的环量误差和速度场误差,发现对于数值模拟的A320 近场尾涡,在计算尾涡环量时,采取3~12 m 的半径区间作为平均值更好,常用的5~15 m 的半径区间并不适用于中型客机的尾涡环量值估算。
3)对比了H-B 和L-O 模型,以数值模拟得到的近场特征参数进行尾涡速度场的构建拟合,发现LO 模型在近场成熟区构建的速度场与原速度场的误差更小,拟合程度更好。
