轨道交通“双U+箱形”截面桥梁剪力滞效应简化计算方法

王珊珊,陈 浩,程 浩,王 俊

(1.中国建筑第八工程局有限公司,江苏 南京 210008;2.南京地铁建设有限责任公司,江苏 南京 211806;3.南京工业大学 土木工程学院,江苏 南京 211800)

“双U+箱形”组合截面梁是箱形梁在城市轨道交通中演化出的一种新型桥梁结构形式,其特征主要体现在:一是U形腹板结构可作为栏板、接触网立柱基础和声屏障等,使附属结构成为桥梁主体结构的一部分[1];二是截面抗弯刚度大;三是腹板较多,腹板与翼板连接处复杂。由于U形和箱形截面梁中均存在剪力滞效应,容易引起翼和腹板连接处局部应力偏大,严重时可导致混凝土开裂。国内外学者对薄壁箱梁剪力滞效应问题进行了大量的试验研究、有限元模拟和理论分析[2-6],但对U形、U形与箱形组合截面的剪力滞效应研究尚未见相关文献报道。

目前,箱梁剪力滞效应解析解计算方法主要有比拟杆法[7-11]和能量变分法[12-19]。赵志峰等[7]采用比拟杆法、有限元法和有机玻璃模型试验分析了单箱三室简支梁及连续梁在均布荷载和集中荷载作用下的剪力滞效应,结果表明:比拟杆法的分析误差总体在10%以内。郭增伟等[8]推导了变截面箱梁加劲杆等效面积和剪力滞效应的微分方程,研究了悬臂梁梁高和腹板厚度变化对剪力滞效应的影响,结果表明:比拟杆法的计算精度较好。孙志伟等[9]提出一种基于反弯点结合比拟杆法和叠加原理的箱梁剪力滞简化计算方法,研究了连续刚构桥的剪力滞效应和有效分布宽度,其剪力滞系数解析解与数值模拟的偏差均在±5%范围内。比拟杆法目前多适用于等截面梁的剪力滞效应问题分析。

采用能量变分法求解剪力滞问题时,计算精度依赖于假定的翘曲位移函数[12-19]。目前,应用较多的翘曲位移函数有抛物线函数、三角函数和双曲线函数。翼板、顶板和底板可以选用不同的抛物线位移函数[12],并考虑剪力滞效应引起的附加挠度[13-14]。截面中性轴的位置可以通过轴力平衡条件来定位[15]。将纵向位移函数定义为剪力滞翘曲位移、初始剪切变形、弯曲、轴向和校正5种变形模式之和[16],并考虑弯曲剪力流对薄壁箱梁弯曲曲率和顶底板纵向翘曲位移差函数的影响[17],考虑梗腋特性参数对翘曲位移的影响[18],对翼板引入受边界条件影响的修正系数[19]。目前,基于能量变分法的计算精度可控制在10%以内,能量变分法可以得到控制微分方程及较高精度的闭合解,既能反映箱梁任意截面上的剪力滞效应分布规律,还能逐一研究各个参数对剪力滞效应的影响。

以南京市宁句线某轨道交通连续U形梁桥为例,通过分析“双U+箱形”组合梁在竖向弯曲时翼板上的剪力流分布规律,引入顶板悬挑段与顶板、底板与顶板剪力流的比来反映截面剪力流对剪切变形的影响,定义各翼板符合其剪切变形规律的翘曲位移函数,利用能量变分法,建立了等截面连续“双U+箱形”梁剪力滞系数计算方法。以一座三跨“双U+箱形”截面连续梁桥为算例,验证自重和轨检车荷载作用下简化计算方法的可靠性,并讨论了梁高和腹板厚度对剪力滞效应的影响。

1 “双U+箱形”组合梁剪力滞效应微分方程

1.1 组合梁翼板剪力流分布规律

翼板的剪切变形由其内部总剪力流(q)的大小决定[20],对于具有2个箱室的“双U+箱形”闭口截面薄壁梁(图1),计算时须沿母线切开2个切口,此开口截面在剪力作用下的剪力流为q0,在每个切口处会有附加剪力流qi(i=1、2),假设截面上的剪力流方向如图2所示。图1和2中,L、L1、Lw分别为截面总宽度、顶板(底板)和顶板悬挑段的宽度;tu、tb、tw分别为顶板、底板和顶板悬挑段的厚度;tf、t′f分别为箱梁部分和U形梁部分边腹板厚度;tz、t′z分别为箱梁部分和U形梁部分中腹板厚度;h1为截面顶部至顶板中性面的距离;h2、h3分别为顶板和底板中性面至截面中性轴的距离;H为截面高度;Qz为计算截面处的剪力;s为剪力流的计算路径。

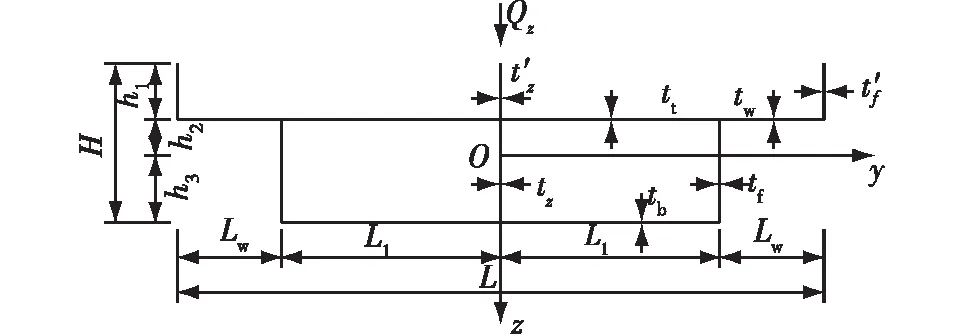
图1 “双U+箱形”截面示意

图2 开口截面剪力流方向

开口截面的剪力流计算公式为[20]

(1)

由式(1)可以看出:“双U+箱形”截面si位置处的剪力流大小由该位置处的Sy决定,剪力流的方向以逆时针为负。经验算,若图2中2号箱室5点处的剪力流满足剪力流平衡原理,则所假设的剪力流路径正确。

对于多室闭口截面薄壁梁,第i室的位移协调条件为[20]

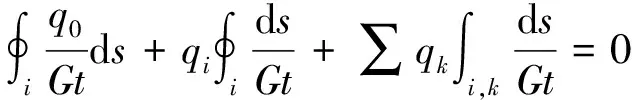
(2)

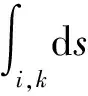
(3)

解得

(4)

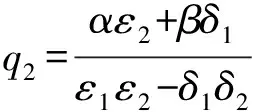
(5)

式中:q1为单箱双室截面左室的附加剪力流;q2为右室的附加剪力流。

利用叠加原理,可得翼板上各点处的剪力流。

顶板悬挑段和两块腹板支撑部分顶板的剪力流比(η1)可通过其交接位置2点处左右两侧位置处剪力流的比来表示,如式(6)所示。

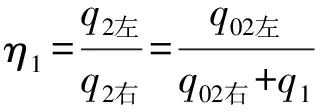
(6)

式中:q02左为开口截面2点位置左侧的剪力流;q02右开口截面2点位置右侧的剪力流;q2左、q2右分别为闭口截面2点位置左侧和右侧的剪力流。

剪力流是由腹板传递给翼板的,则底板和顶板的剪力流比(η2)可通过边腹板2和4点处剪力流的比来表示,如式(7)所示。

(7)

式中:q04上为开口截面箱形部分中腹板4点位置上侧的剪力流;q2下、q4上分别为闭口截面2点位置下侧和4点位置上侧的剪力流。

1.2 翼板剪滞翘曲位移函数

“双U+箱形”组合梁在对称挠曲时,翼板会发生剪切变形,已不满足平截面假定,这时不能仅用竖向挠度w(x)来描述其挠曲变形,故定义w(x)为梁的竖向挠度,u(x)为剪切转角的最大差值,u(x,y,z)为梁的纵向位移,f(y,z)为剪滞翘曲位移函数。假定翼板的纵向位移沿横向为三次抛物线分布,基于各翼板剪力流分布规律,分别定义各翼板的剪滞翘曲位移函数。“双U+箱形”截面几何参数如图3所示,其中2b1、2b2、b3分别为顶板、底板和顶板悬挑段的宽度;2t1、2t2、2t3分别为顶板、底板和顶板悬挑段的厚度;a1、a2、a3分别为中腹板、箱梁部分和U形梁部分边腹板厚度;b4=b2+a1/2;b5=b1+b3+a2;b=2(b4+b5+a3)。

图3 “双U+箱形”截面几何参数

此时,梁截面各翼板的纵向位移u(x,y,z)可表示为

(8)

式中:Zi为截面形心到顶板、顶板悬挑段或底板的距离。

由于箱形截面的剪切变形与截面上剪力流的分布有关[20],本文假定翼板的纵向位移沿截面横向为三次抛物线分布,并考虑截面剪力流对剪切变形的影响,在基于剪切变形规律的翘曲位移函数中引入顶板悬挑段和顶板的剪力流比(η1),底板和顶板的剪力流比(η2)的影响,如式(9)所示。

(9)

式中:f1(y,z)、f2(y,z)、f3(y,z)分别为顶板、顶板悬挑段和底板的翘曲位移函数。

1.3 控制微分方程及闭合解

1.3.1 结构总势能

(10)

式中:M(x)为梁截面承受弯矩。

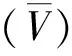
(11)

则体系的总势能(∏)为

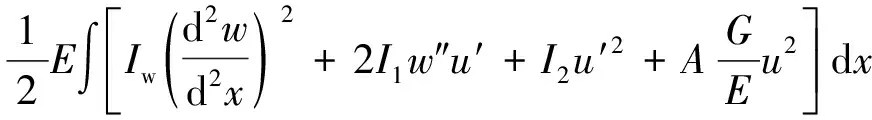
(12)

1.3.2 微分方程与边界条件

基于变分法原理,对式(12)进行变分运算,得到微分方程,如式(13)所示。

(13)

式中:I为组合截面惯性矩。

整理式(13),并令

(14)

可得

(15)

式中:φ、k为常数;Q(x)为梁截面承受的剪力。

其中,u(x)可根据梁的荷载情况、边界条件和计算截面位置确定。

1.3.3 截面上的应力与附加弯矩

由式(13)可得,附加弯矩(MF)可表示为

MF=EI1u′(x)

(16)

则梁截面上任一点纵向应力(σx)的表达式为

(17)

代入式(9)可得各翼板的应力表达式。

1.4 连续梁桥的剪力滞效应求解

由式(15)可知,简支梁在均布荷载和集中荷载作用下的剪切转角最大差值u(x)可分别由相应荷载工况下的边界条件和连续条件求得。

对于连续梁,可先取一基本体系(一般取简支梁),然后分别将荷载和解除的超静定反力施加在基本体系上,最后利用叠加原理进行求解[20],如式(18)所示。

(18)

2 算例分析

以南京市宁句线某轨道交通一座跨度为35 m+50 m+35 m的连续U形梁桥截面为例,实际截面尺寸如图4所示。为方便计算,简化后的截面形式及计算点位置如图5所示,混凝土为C60,集中荷载以轨检车辆荷载为例,轨检车轴距、轴重及加载位置如图6所示,其中最不利荷载位置由跨中截面弯矩影响线求得。由于主梁中跨跨中截面纵向应力变化及剪力滞效应较边跨跨中明显[21],故选取中跨跨中截面作为计算截面。

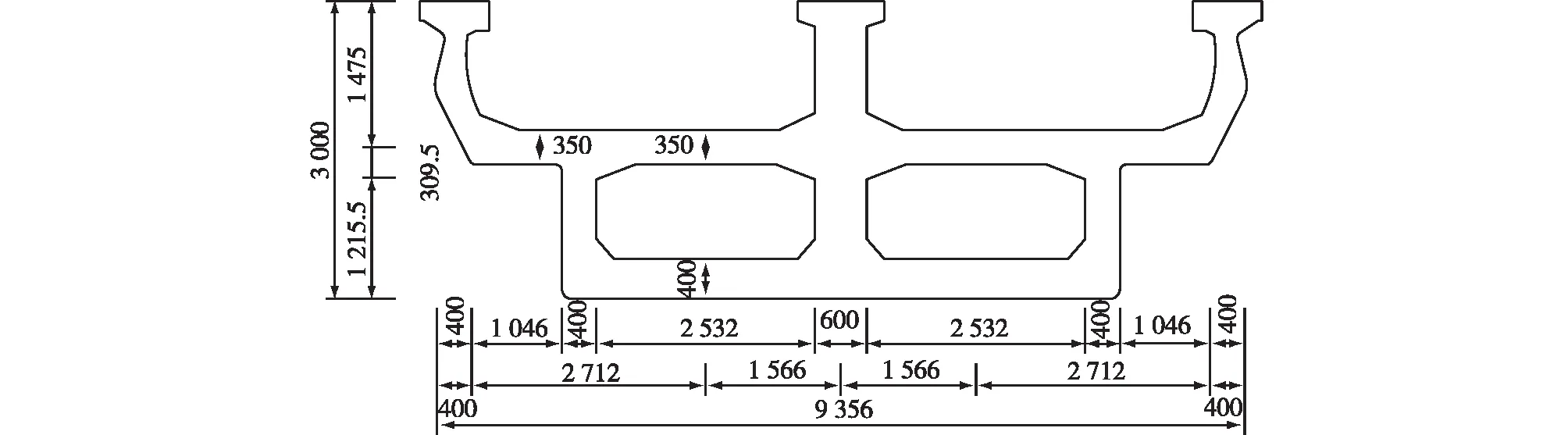
图4 实际工程截面(mm)

图5 简化后的截面及计算点位置(mm)

图6 轨检车轴距、轴重和加载位置(mm)

ABAQUS模型采用八节点六面体线性减缩积分(C3D8R)单元,并划分为六面体网格,边界条件和荷载施加与连续梁算例相同,算例的三维有限元局部模型如图7所示。

图7 截面有限元模型

2.1 自重作用下连续梁的剪力滞效应

在实际工程中,自重是桥梁结构的主要荷载形式。以上述三跨等截面连续梁算例为例,将自重和超静定支座反力单独作用下基本体系的计算截面弯矩M(x),顶板与其悬挑段的翘曲位移函数f(y,z),剪切转角最大差值的一阶导数u′(x)分别代入式(17),然后根据式(18)计算得中跨跨中截面顶板的剪力滞系数,并与有限元仿真结果进行对比分析。图8和9分别给出了自重作用下中跨跨中截面的应力云图和顶板的剪力滞系数分布。由图8和9可以看出:截面表现出正剪力滞的现象,与腹板的距离越远,顶板剪力滞系数越小,顶板悬挑段的剪力滞系数比腹板支撑部分顶板的小4%。中跨跨中截面处的剪力滞系数简化计算解和有限元数值解的吻合程度较好,最大偏差在1%以内。

图8 自重作用下跨中截面应力云图(MPa)

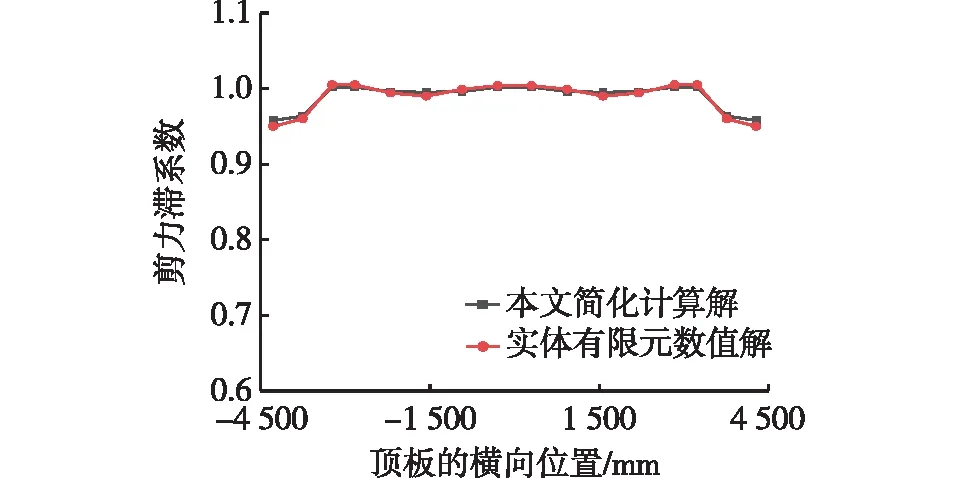
图9 自重作用下顶板剪力滞系数分布对比

2.2 轨检车荷载作用下连续梁的剪力滞效应

在实际工程中,列车荷载是轨道交通桥梁结构承受的主要活荷载。为简化计算,以轨检车荷载为例,将轨检车荷载和超静定支座反力单独作用下基本体系的计算截面弯矩M′(x)、f′(y,z)和u″(x)分别代入式(17),然后根据式(18)计算得中跨跨中截面顶板的剪力滞系数,并与有限元仿真结果进行对比分析。图10和11分别给出了轨检车荷载作用下中跨跨中截面的应力云图和顶板的剪力滞系数分布。由图10和11可以看出:轨检车荷载作用下的剪力滞系数变化趋势与自重作用时基本一致,顶板悬挑段的剪力滞系数比腹板支撑部分顶板的小32%,比自重作用下的变化更加明显。轨检车荷载作用下的剪力滞系数简化计算解与有限元数值解的最大偏差在4%以内。

图10 轨检车作用下跨中截面应力云图(MPa)

图11 轨检车荷载作用下顶板剪力滞系数分布对比

2.3 梁高和腹板厚度对剪力滞效应的影响

为进一步探究“双U+箱形”截面梁剪力滞效应的影响因素,分别选取梁高、边腹板厚度和中腹板厚度3个参数作为变量,研究单一变量下截面上的剪力滞效应。以上述三跨连续梁算例为模板,在保持U形部分高度和腹板厚度不变的条件下,将梁高分别调整为2.5、3.0、3.5和4.0 m;在保持梁高和中腹板厚度不变的条件下,将边腹板厚度分别调整为250、300、350和400 mm;在保持梁高和边腹板厚度不变的条件下,将中腹板厚度分别调整为300、400、500和600 mm,分析单一变量下剪力滞系数的变化情况,探究梁高、边腹板和中腹板厚度对剪力滞效应的影响。

图12、13和14分别给出了梁高、边腹板厚度和中腹板厚度对连续梁中跨跨中截面及主梁中跨各梁截面腹板与顶板交接处剪力滞系数的影响。由图12、13和14可知:在中跨反弯点附近,腹板与顶板交接处的剪力滞系数小于1,出现了负剪力滞现象;在中跨反弯点处弯矩为0,此时剪力滞系数出现奇异现象,出现间断跳跃点;在组合截面U形部分高度不变的条件下,箱形部分与U形部分高度之比为0.5～1.5,随着比值的减小,剪力滞系数逐渐减小;随着边腹板厚度的增大,剪力滞系数逐渐减小;随着中腹板厚度的增大,剪力滞系数逐渐减小,但中腹板的影响程度相对较弱。

图12 梁高对顶板剪力滞系数的影响

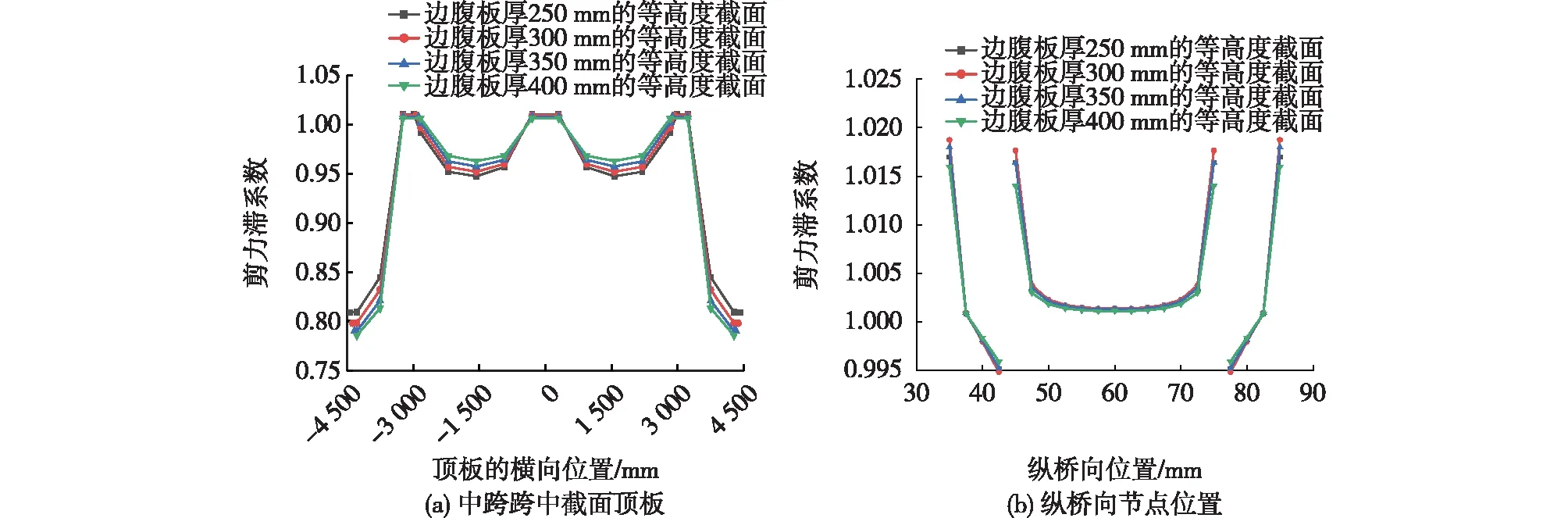
图13 边腹板厚度对顶板剪力滞系数的影响

图14 中腹板厚度对顶板剪力滞系数的影响

3 结论

基于能量变分法建立了“双U+箱形”截面连续梁剪力滞效应简化计算方法,以三跨等截面连续梁为算例,分别验证了在自重和轨检车荷载单独作用下该简化计算方法的可靠性,并讨论了梁高和腹板厚度对剪力滞系数的影响。

1)通过分析截面上剪力流的分布规律,考虑截面剪力流对剪切变形的影响,在基于剪切变形规律的翘曲位移函数中引入顶板悬挑段和顶板的剪力流比、底板和顶板的剪力流比的影响,基于能量变分法推导了等截面连续梁剪力滞系数计算公式。

2)在自重和轨检车荷载作用下,中跨跨中截面的剪力滞系数变化趋势基本一致,但相对于自重作用,轨检车荷载作用下的剪力滞效应更明显。轨检车荷载作用下顶板悬挑段的剪力滞系数比腹板支撑部分顶板的剪力滞系数小32%,而自重作用下顶板剪力滞系数分布比较均匀。剪力滞系数简化计算解与有限元数值解吻合较好。

3)梁高和腹板厚度的变化均会削弱截面的剪力滞效应,但相对于梁高和边腹板厚度,中腹板厚度变化对剪力滞系数的影响程度较弱。因此,在桥梁工程的设计阶段,可通过选择合适的梁高和腹板厚度以削弱剪力滞效应。