辅助线法解几何问题中的“截长补短”思想
2023-06-14闵文彬
数理天地(初中版) 2023年5期
闵文彬

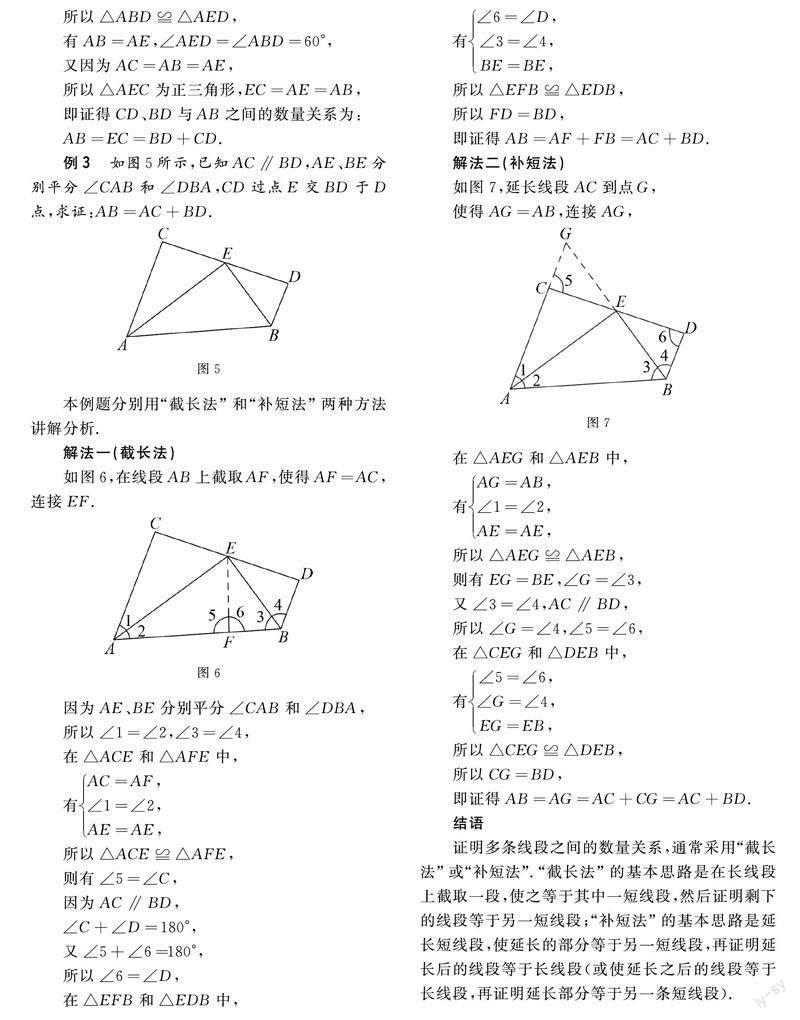
【摘要】平面几何中解决多条线段之间的数量关系问题,常常借助于作辅助线构造相似三角形或全等三角形,根据它们对应边、角之间的关系来解得线段间的数量关系.“截长补短”思想是辅助线法的核心思想,可以为构造相似三角形或全等三角形创造出重要条件.本文列舉三个通过“截长补短”思想讨论多条线段之间数量关系的问题,阐述“截长补短”思想的应用思路,希望能够促进学生几何解题技巧的提升.
【关键词】截长补短;平面几何;三角形
结语
证明多条线段之间的数量关系,通常采用“截长法”或“补短法”.“截长法”的基本思路是在长线段上截取一段,使之等于其中一短线段,然后证明剩下的线段等于另一短线段;“补短法”的基本思路是延长短线段,使延长的部分等于另一短线段,再证明延长后的线段等于长线段(或使延长之后的线段等于长线段,再证明延长部分等于另一条短线段).
