基于灵敏度分析的结构损伤识别方法研究

余洁歆,林 伟,陈 欣,谢本飞

(1.福建江夏学院 工程学院,福建 福州 350108;2.福州大学 土木工程学院,福建 福州 350108;3.福州桂武置业有限公司,福建 福州 350011)

随着我国经济持续稳定增长叠加城镇化的高速推进,土木行业实现了快速发展。大量重大工程结构,如高层建筑、大跨桥梁、大型水利工程等不断涌现。在其漫长的服役期内,由于环境侵蚀、日常超载、材料性能退化等原因可能导致结构性能退化,或受到自然灾害如地震、台风等侵袭,导致不同程度的损伤、区域功能瘫痪,甚至倒塌。如2001年宜宾南门大桥因吊杆断裂导致部分桥面垮塌[1];2004年法国巴黎戴高乐机场候机楼屋顶局部坍塌[2];2007年美国明尼苏达州一座跨越密西西比河的I-35W大桥由于节点板破坏导致整桥坍塌,造成13人死亡和145人受伤[3]。

我国基础设施体量庞大,随着其服役时间的增加,逐渐进入病害集中暴露期,迎来养护高峰,结构维护管理费用的压力愈发严重。为此,需利用健康监测手段尽早发现隐患,保障工程结构安全并实现预防性维护管理。

尽管不少结构已经安装了健康监测系统,如日本明石海峡大桥、美国金门大桥,我国青马大桥、虎门大桥、广州电视塔等[4-10]。由于监测数据与结构损伤相关性弱,又缺乏对海量数据的有效处理方法,导致捕捉局部损伤犹如大海捞针。利用观测数据对所监测结构进行分析和反演,进而定位与量化损伤,实则为一种逆分析理论。但工程结构复杂、体型庞大,难以获取完备信息,使得求解方程容易出现病态,其准确性受限于海量的冗余信息。现有技术在实现结构安全评价和预警方面仍存在众多困难,如何从海量监测数据分析结构损伤性能成为重点要研究的问题[11-12]。

模态参数作为结构的自身固有属性,在结构发生损伤时会随之改变。为探求损伤对模态参数的影响,寻求能够准确评估结构健康状况的方法,本文从模态参数的灵敏度出发,根据结构模态参数与设计参数之间的近似关系,推导了结构的一阶灵敏度分析方程,以此建立基于灵敏度分析的损伤识别程序。对5层框架结构进行数值模拟,揭示模态参数的敏感性。通过选取合适的模态参数,对结构损伤位置和损伤程度进行识别,验证了该方法的有效性和准确性。

1 基于灵敏度的有限元模型修正方法

1.1 灵敏度分析理论

有限元模型修正方法的基本思想是以结构有限元模型和试验模型之间的差值为目标函数,通过修正设计参数,使修正后的模型与试验模型的整体信息趋于近似,广泛应用于各工程领域[13-14]。灵敏度理论是通过模态参数与损伤指标之间的一阶导数,构造两者间的近似线性关系。

假定r为初始有限元模型设计参数,fi为结构模态参数,且为r的函数,当参数r发生微小变动时,第i阶模态参数f对r的一阶泰勒展开式为:

(1)

式(1)可改写为:

△f=S|m×n△r

(2)

式(2)中,△r为设计参数修正值向量;△f为模态参数的残差向量,是受损结构模态参数与初始有限元模型模态参数的差值。通过最小化残差,实现损伤指标反演。由于两者间为近似关系,为确定损伤指标的准确幅值,需经历反复迭代。S为灵敏度矩阵,m表示所取特征参数的阶数,n表示待修正设计参数的个数。求解灵敏度矩阵S即是求特征参数对设计参数的导数,如式3所示。

(3)

1.2 特征值的灵敏度

无阻尼结构的第i阶特征方程为:

(K-Mλi)Φi=0

(4)

式(4)中,K为结构刚度矩阵,M为结构的质量矩阵,Φi为第i阶特征向量,λi为第i阶特征值。

对式(4)求关于设计参数rj的导数:

(5)

(6)

结构的刚度矩阵和质量矩阵均为对称矩阵,式(4)转置可得:

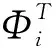
(7)

因此式(6)中第三项为零,可简化为:

(8)

采用正则振型对结构质量矩阵和刚度矩阵进行归一化,可得:

(9)

(10)

将式(9)代入式(8)可得第i阶特征值关于设计参数r的灵敏度表达式:

(11)

1.3 特征向量的灵敏度

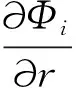
(12)

(13)

将式(9)和式(10)代入式(13)可得:

(14)

根据式(14)可得:

(15)

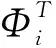
(16)

式(16)中的各项均为标量,其中第一项表达式:

(17)

将式(17)代入式(16),可得:

(18)

将式(12)代入式(18),可得:

(19)

将式(9)和式(10)代入式(19),可以得到当i=j时的系数为:

(20)

整理可得特征向量关于设计参数的灵敏度表达式:

(21)

2 损伤识别的程序实现

使用ANSYS和MATLAB软件编写基于灵敏度分析的损伤识别程序,具体流程如图1所示。

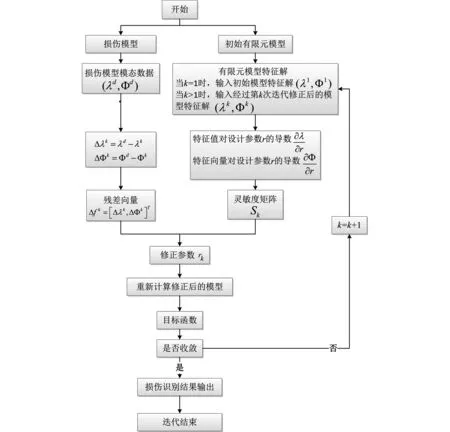
图1 基于灵敏度分析的损伤识别流程图

选取杨氏模量作为待修正参数r,通过降低某指定单元的杨氏模量模拟损伤单元。编写特征值和特征向量对待修正参数r的一阶偏导数程序,组成灵敏度矩阵Sk。利用结构动力特性进行待修正参数的修正,最小化待修正模型和损伤模型之间的差值,直至优化过程收敛。采用刚度降低因子SRF作为识别输出结果,表示修正参数的变化量△r与初始值r的比值,以确定损伤位置、量化损伤程度。

3 结构损伤识别数值仿真

3.1 有限元模型

对5层空间框架结构进行数值研究,框架结构如图2所示。整体由24个节点组成,其中最底部4个节点为固定端,每个节点有6个自由度,共120个自由度。

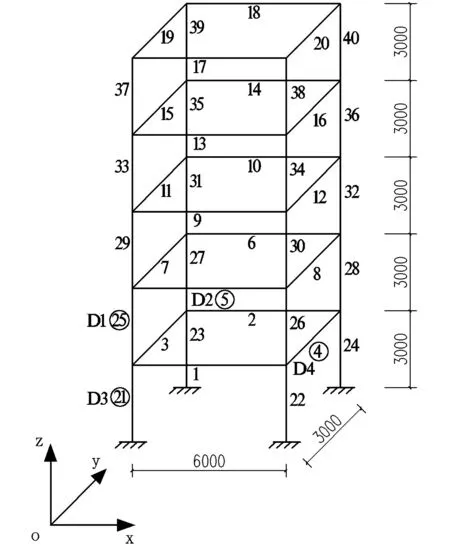
图2 5层框架结构模型

图2中编号为单元编号,共40个,单元特性:截面积为0.25m2,杨氏模量E为3.5×104MPa,质量密度为2500kg/m3。利用MATLAB软件编写各节点的坐标信息和单元信息,组成5层框架结构的刚度矩阵和质量矩阵,通过模态分析得到结构频率和振型。

3.2 损伤程度对特征参数的影响

为研究特征参数对损伤程度的敏感性,分别设置二层柱单元E25和二层梁单元E5(如图2“D1”和“D2”)为损伤单元,将损伤程度由10%逐级递增到90%来对单个单元进行损伤模拟,观察随着损伤程度的提高,结构低阶特征参数的变化。变化情况采用特征值的相对变化率Diff和模态置信因子MAC(Modal Assurance Criterion)体现,定义如式(22)和(23)所示。

(22)

(23)

当MAC数值为1时表明两组模态振型完全相关;数值为0时表明两组模态振型完全无关。

D1损伤前后的结构特征参数的变化,限于篇幅,仅列举损伤程度为50%和90%的工况下,结构前7阶模态和前20阶均值分析结果如表1所示。

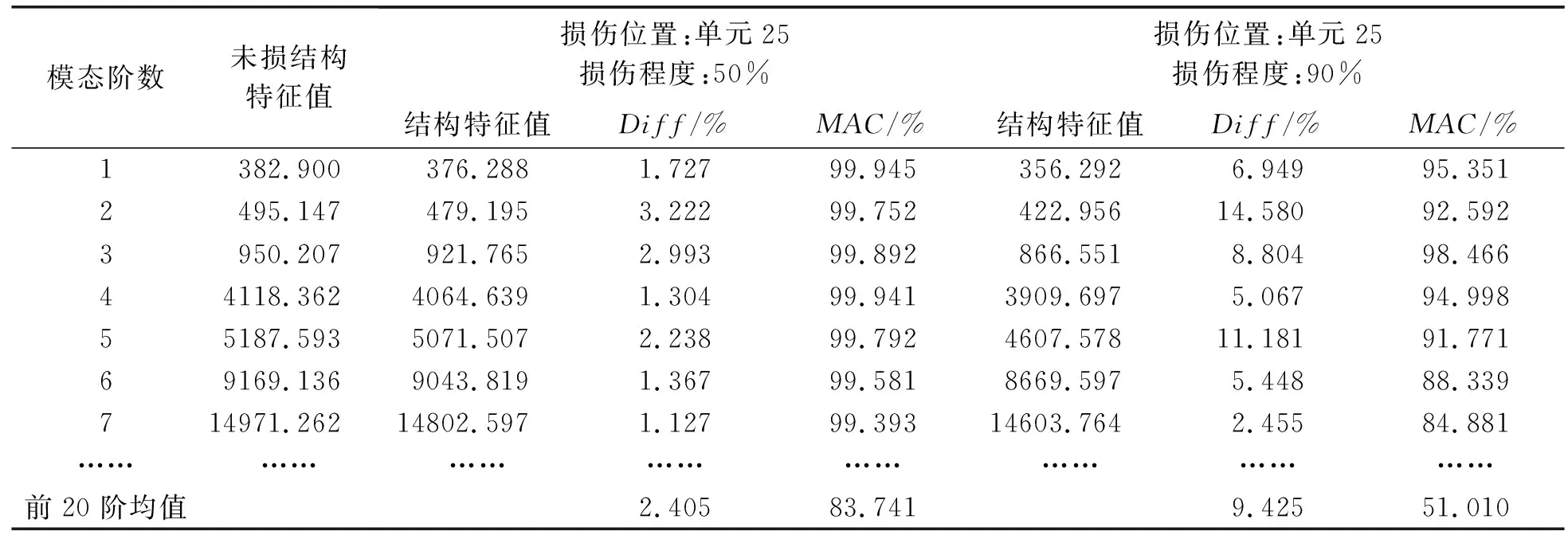
表1 不同损伤程度的结构特征参数

由表1中可以看出,与未损伤状态相比,损伤结构的特征值和MAC明显降低。当损伤程度为50%时,引起的模态参数变化幅度不大,前20阶Diff和MAC均值分别为2.405%和83.741%,说明局部小损伤对整体结构的特征值和振型影响较小。当损伤程度上升到90%时,特征参数变化幅度明显增大。其中第2特征值受损伤影响较大,特征值相对变化率为14.580%,第6和7阶特征向量受损伤影响较大,MAC值分别为88.339%和84.881%。结构前20阶Diff和MAC均值分别为9.425%和51.010%,振型变化较大。

损伤程度从10%递增到90%的9种工况前7阶特征值和特征向量的变化情况,D1损伤情况下,如图3和图4所示。

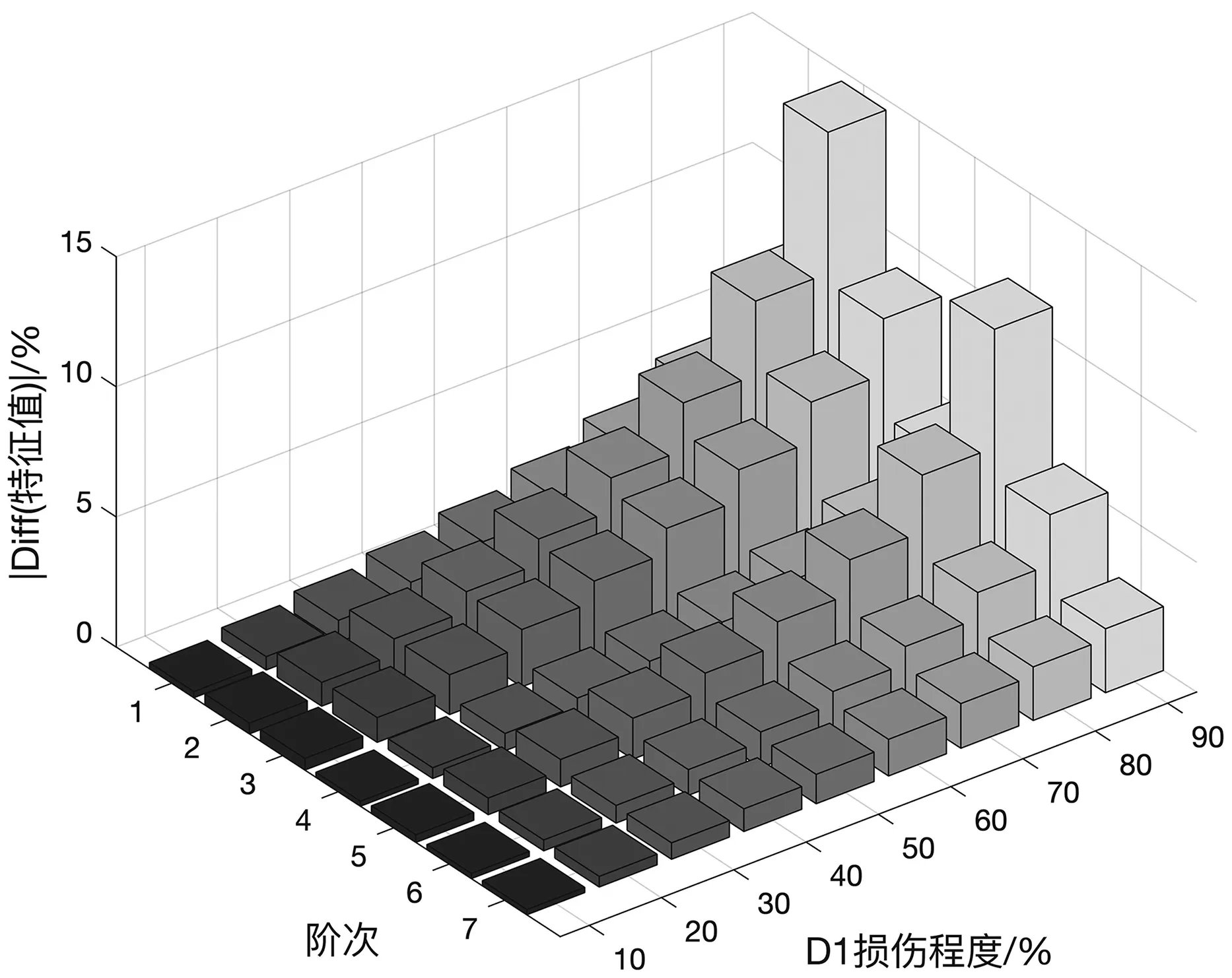
图3 D1工况特征值随损伤程度的变化

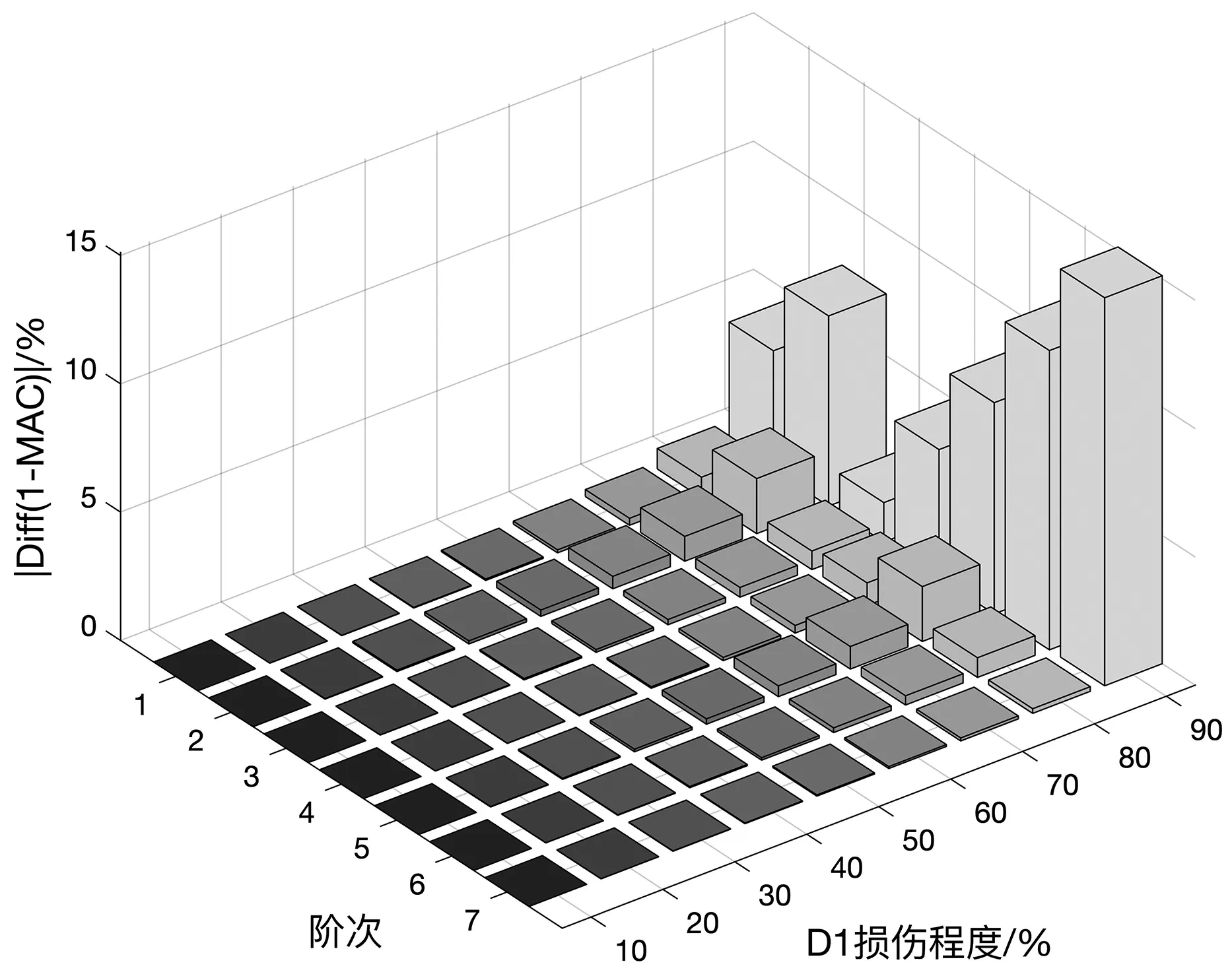
图4 D1工况MAC随损伤程度的变化

由图3和图4可以看出结构特征参数的变化与损伤程度成正相关。当损伤程度小于50%的工况下,前7阶特征值相对变化率均小于4%,MAC最小值为99.393%,表明该程度损伤引起的特征参数变化幅度较小。随着损伤程度的上升,特征参数变化幅度明显增加。当损伤程度为90%时,前6阶特征值变化率均大于5%,各阶特征向量产生较大变化,D2梁损伤单元的9种不同损伤程度工况下的特征参数变化,如图5和图6所示。

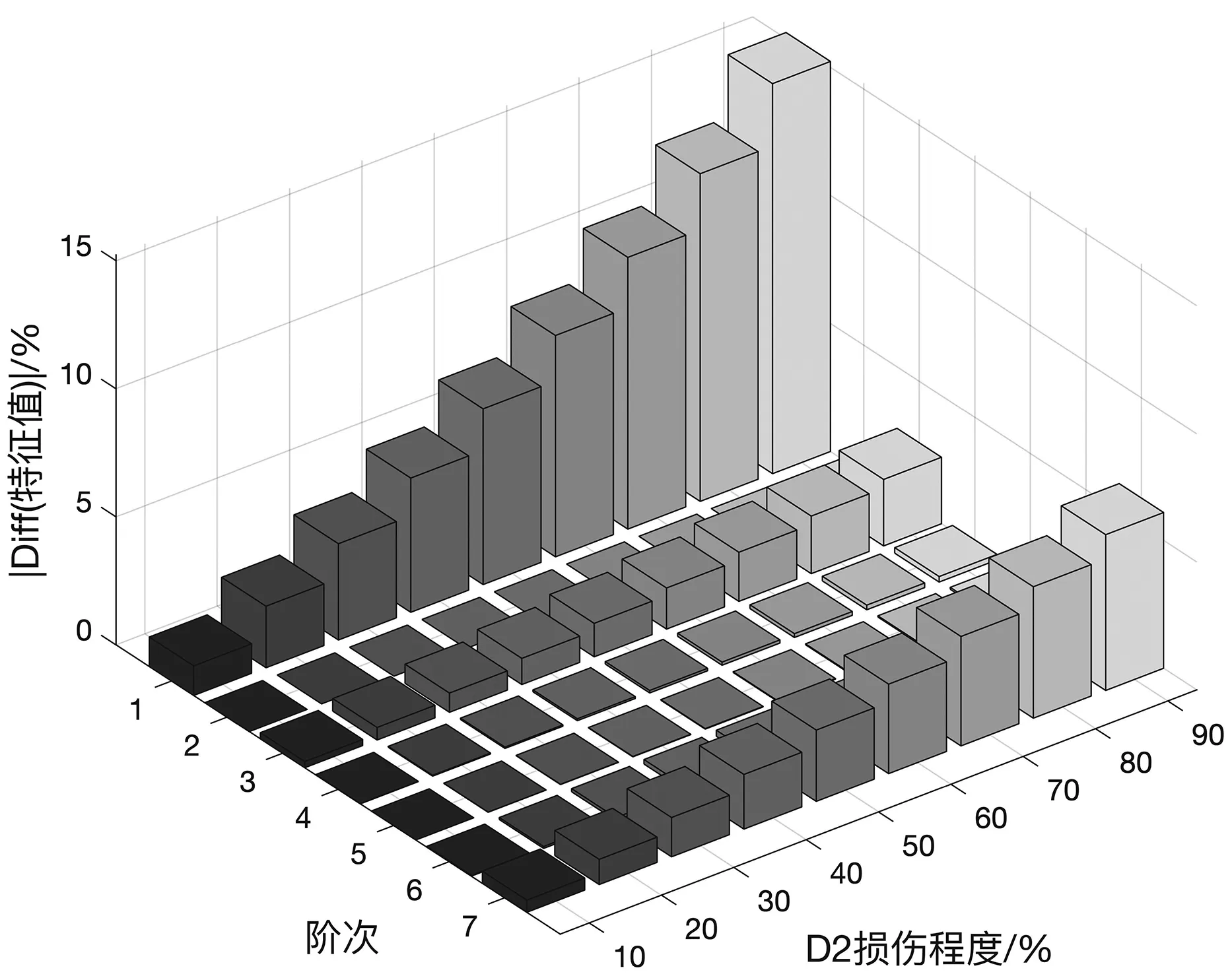
图5 D2工况特征值随损伤程度的变化

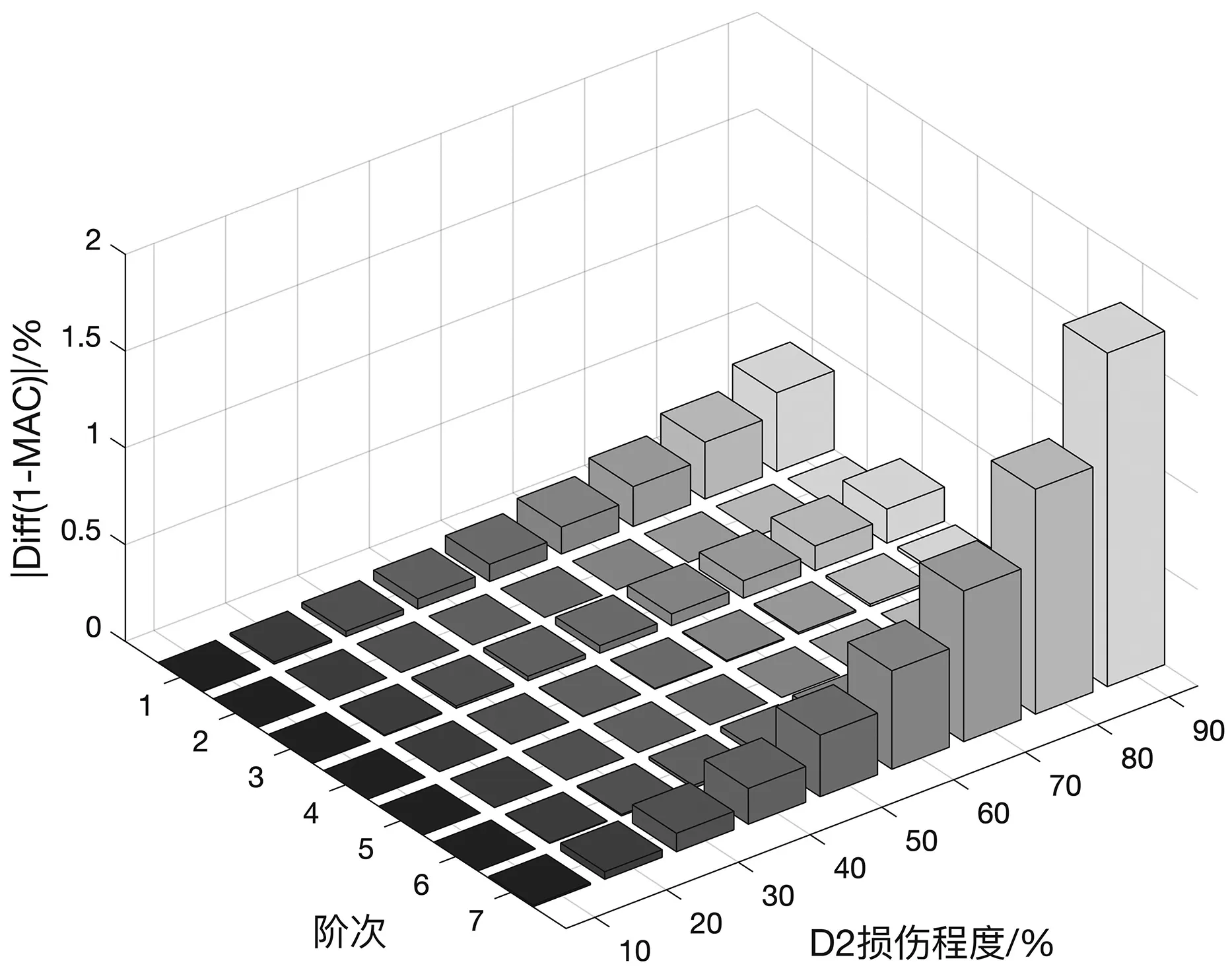
图6 D2工况MAC随损伤程度的变化

由图5和图6可以看出柱单元和梁单元受损的变化趋势基本一致。从损伤引起的特征值变化幅度来看,当D2损伤程度为50%的工况下,第1阶特征值相对变化率最大为6.860%,其余阶次特征值相对变化率均小于3%。当损伤程度同为90%工况下,梁损伤单元最大特征值变化率为15.228%,与柱损伤引起的最大变化率相近。但其最小MAC值为98.276%,而柱单元最小MAC值为84.881%,说明梁损伤单元产生的结构模态数据变化更为微小,容易被噪声掩盖。

3.3 损伤位置对特征参数的影响

为探究结构特征参数对损伤位置的敏感性,保持单元受损程度不变,设置每种工况的损伤位置由结构第一层依次上移到顶部第五层。受损单元类型分为柱单元和梁单元两种情况讨论,例如首层受损单元如图2“D3”和“D4”,每个工况中构件的损伤程度均为50%。特征参数随损伤位置的变化情况,如图7所示。

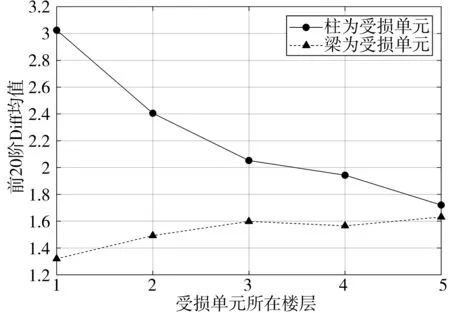
图7 D3和D4工况特征值随损伤位置的变化

当损伤单元为柱时,结构特征值的变化幅度随着损伤楼层的上移而逐渐降低。损伤柱单元位于首层时,前20阶特征值相对变化率均值为3.03%,而损伤柱单元位于5层时,相对变化率均值下降到1.72%。相较于底层柱,当损伤单元位于高楼层时更难被发现。当受损单元为梁时,结构特征值没有随着损伤位置的移动发生明显的改变,特征值变化幅度都较小,前20阶特征值相对变化率均值在1.65%以下。由此可见梁单元对结构低阶动力特性的贡献小于柱单元,在仅使用低阶特征值时将难以被准确识别。

通过损伤程度和位置对模态参数的影响可以发现,损伤实质是局部现象,对整体结构模态数据产生的变化可能是微小的。而各阶模态对损伤的敏感程度不同,在构建目标函数和灵敏度矩阵时宜选择对损伤敏感的模态,以提高计算效率。

3.4 损伤识别数值分析

以D2工况作为单一局部损伤识别,通过所提出的方法和程序识别损伤位置,量化损伤程度。首先仅以频率作为损伤检测指标,选取前8阶特征值作为方案1进行模型修正,方案1的损伤识别结果,如图8所示。

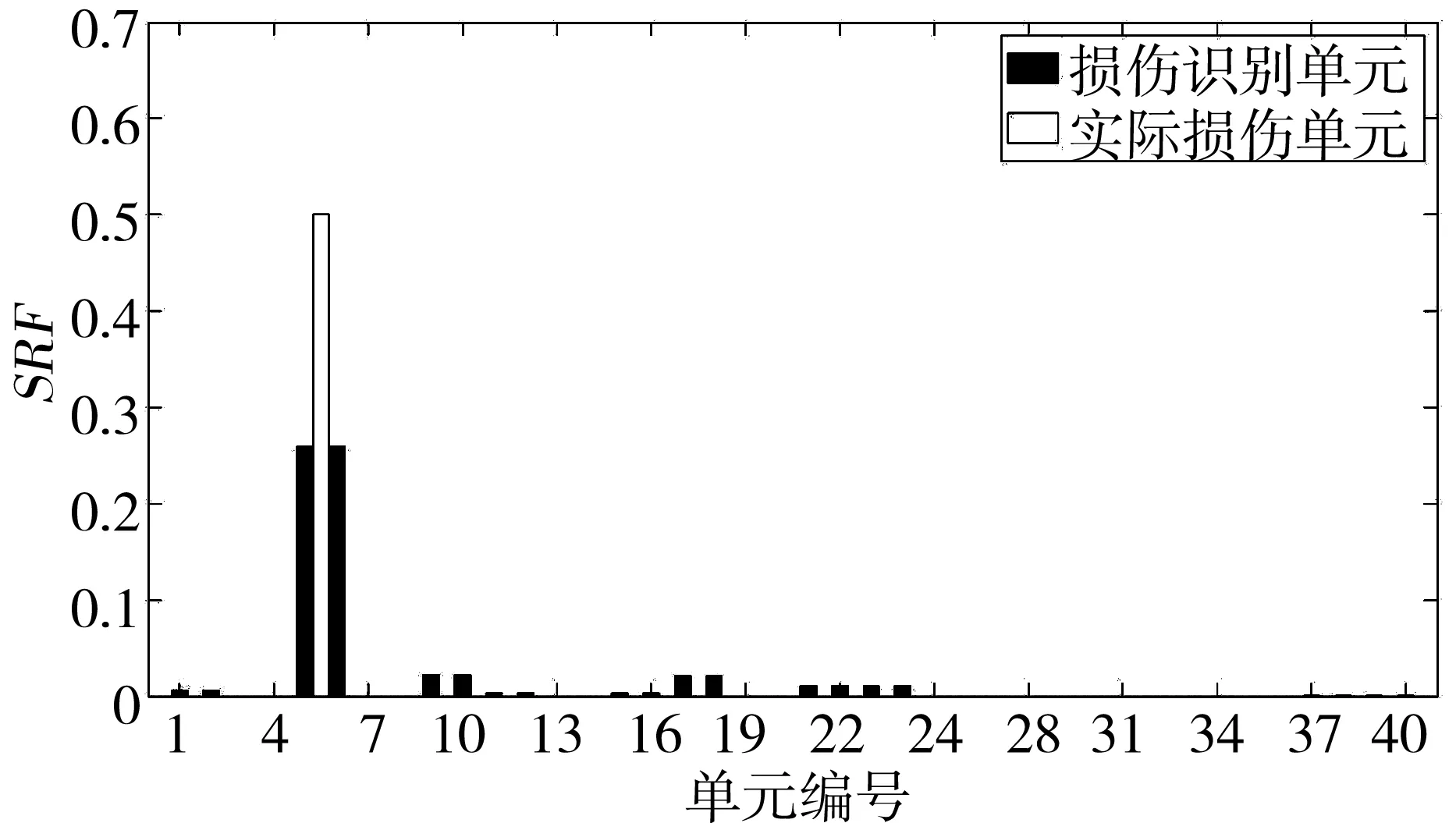
图8 单一损伤工况方案1的损伤识别结果

由图8的识别结果可以看出,识别结果出现了误判,将同层对称梁单元E6识别为损伤单元,真实损伤单元E5的SRF值仅为25.93%,远小于实际损伤50%。

频率是容易获得且精度较高的全局量,但不同损伤工况可能导致相同的频率改变,因此出现误判。并且在损伤程度为50%的工况下,各阶特征值变化幅度较小,前8阶特征值变化率均值仅为1.858%。当损伤引起特征值改变不明显的情况下,仅利用特征值进行损伤识别是不够的。模态振型具有结构振动的空间特性,可以提供结构局部信息,因此利用频率与振型共同作为损伤检测指标进行识别。

在原特征值截取方案1的基础上,增加前4阶模态振型,形成方案2,构建目标函数和灵敏度矩阵。考虑各阶模态对损伤的敏感程度不同,通过对比损伤前后模态分析,发现节点扭转自由度数值较小,为避免冗余信息干扰,产生病态反演及收敛性差等问题,在构建灵敏度矩阵时从全部自由度中删除贡献较小的扭转自由度。采用频率与振型进行模型修正,经过77次迭代后的单一损伤工况方案2的损伤识别结果,如图9所示。

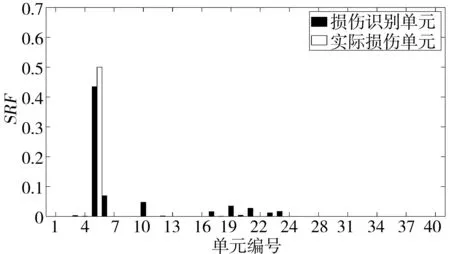
图9 单一损伤工况方案2的损伤识别结果

相比方案1,方案2的识别结果准确定位了实际损伤单元,避免了误判。E5单元相应的SRF值为43.46%,识别精度高,收敛速度快,验证了该方法在单一局部损伤工况下的可行性和准确度。

以D3和D4作为损伤单元进行多损伤工况识别,分别设置E21单元损伤程度为40%,E4单元损伤程度为50%,方案2采用频率与振型进行模型修正的损伤识别结果,如图10所示。

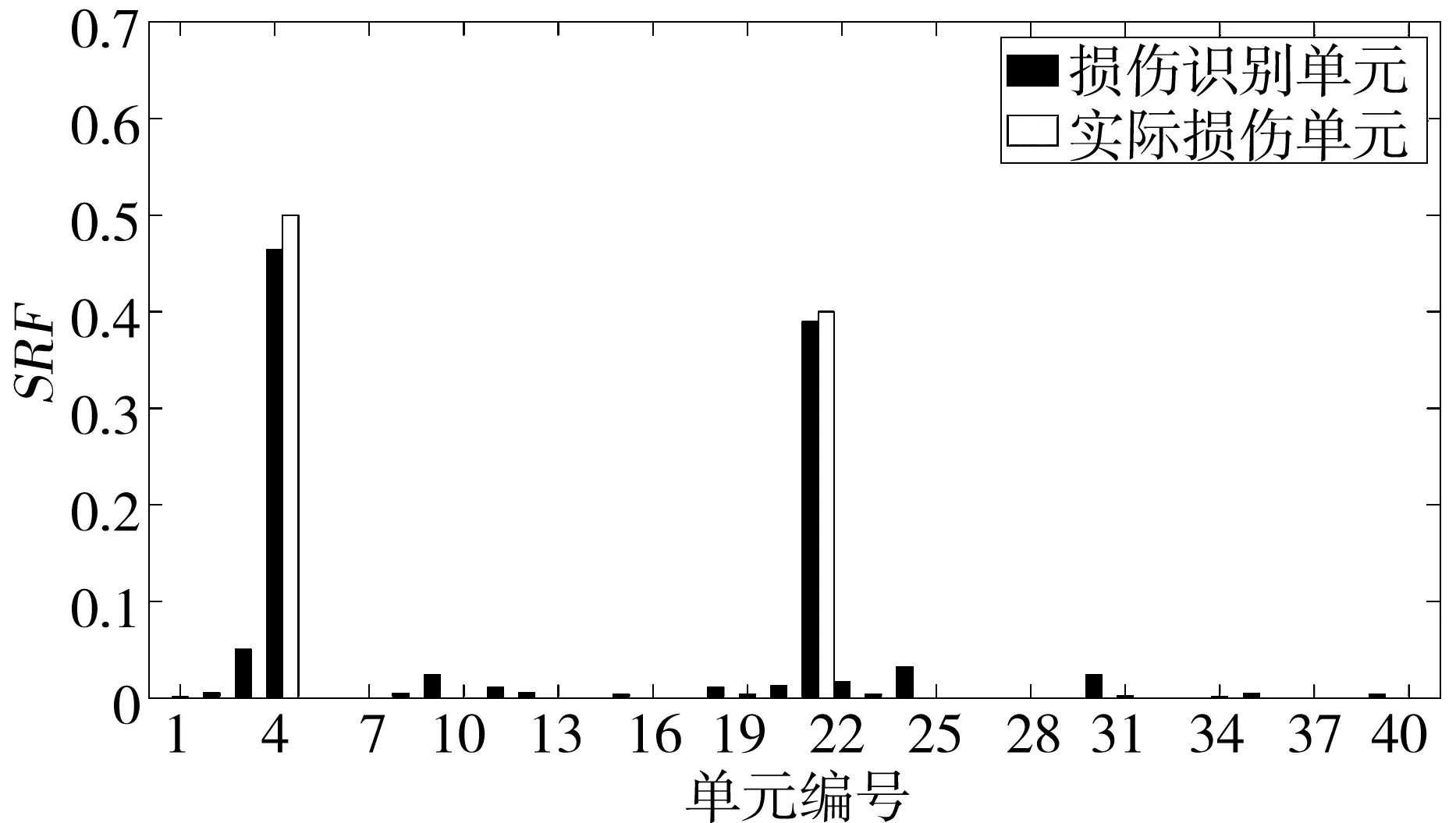
图10 多损伤工况方案2的损伤识别结果

通过200次迭代,准确定位到了损伤单元,且E21和E4相应的SRF值为38.97%与46.44%,与实际损伤值40%和50%相对误差仅为2.58%和7.12%,其余未损伤单元SRF值均未达到10%,抗干扰强,损伤识别精度满足多损伤工况下的要求。

4 结论

文中推导了结构特征参数的灵敏度表达式,以此建立基于灵敏度分析的损伤识别程序。以5层框架结构为数值模型,通过构建不同损伤指标方案反演模型,具体结论如下:

(1)结构特征值和特征向量的变化与损伤程度成正相关,若单元损伤程度较低,则引起的参数变化幅度较小。相较于底层柱,位于高楼层的柱损伤引起的特征值变化幅度更小。由于各阶模态对损伤的敏感程度不同,识别过程涉及大量未知参数,为减少数据量存储,避免病态辨识问题,在构建目标函数和灵敏度矩阵时,需通过损伤前后模态差分析找出对损伤敏感的模态,避免冗余信息干扰,产生病态反演及收敛性差等问题。

(2)从识别结果可以看出,本文提出的基于灵敏度分析的损伤识别方法对于结构局部损伤识别是可行的,且满足精度要求。损伤所导致自振频率和振型的改变,可以反推结构损伤位置和大小。在局部损伤引起特征值变化不明显的情况下,仅利用低阶特征值进行损伤识别可能引起误判。无论是单损伤或多损伤的工况下,同时利用频率与振型进行损伤识别,可以更好的反演结构损伤信息,提升识别的准确性。