基于LBES-SVM的室内UWB定位研究

冯 涛,张 梅

(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)

超宽带(Ultra-Wideband,UWB)技术[1-2]是一种无线通信技术。UWB技术的出现提升了高精度定位领域的水平,解决了许多无线技术方面的难题。UWB信号具有穿透能力强、抗干扰能力好的优点,使其在智能定位系统、无线传感等领域都有广泛的应用[3]。UWB技术应用于室内定位,可以实现高定位精度。当室内的环境较为复杂时,通信信号会受到室内障碍物的阻碍。尽管UWB具有较强的抗干扰能力,由于障碍物的阻碍导致有非视距(Non-Line of Sight,NLOS)误差产生。而且在信号受到较强干扰时,数据也会发生波动,最终会影响室内定位精度。所以UWB在NLOS情况下的定位精度问题成为研究重点,如何改进算法来提高UWB定位精度成为研究的热点。

目前,张碧仙[4]提出了一种改进的基于超宽带UWB技术的TDOA定位方法。在定位基站与定位标签之间采用UWB技术,通过Chan算法对获得的TDOA观测数据进行位置解算,采用加权最小二乘法(WLS),能够有效降低多径和NLOS对定位精度的影响;ZHOU N[5]提出了粒子滤波算法,该算法具有较少的计算时间,在粒子滤波定位中融入到达角测量,平均提高了三维定位精度。李景文等人[6]利用EKF对两者进行融合改进,以此发挥各自技术优势,结果表明该EKF算法有效地减小了误差,提升了室内定位的精度。

目前应用较多的UWB定位算法为最小二乘定位算法(Least Square,LS)。LS是一种常用的数学优化算法,ZHANG Y K等人[7]对UWB定位直接矩阵算法进行了优化,并采用最小二乘矩阵法对定位数据进行处理,以获得更精确的位置坐标。

但是在室内空间较为狭窄情况下,该定位算法的垂直方向定位精度不高,而且由于NLOS环境,导致定位误差较大。为提高室内NLOS环境下超宽带信号受干扰的定位精度,本文提出一种改进的秃鹰搜索算法来优化支持向量机模型,并将其用于定位坐标的修正。将LS初次定位的坐标数据和实际坐标输入到模型中进行训练和测试,最终输出修正后结果。实验与测试结果表明,该方法成功减少了初次的定位误差,最终提高了UWB技术的定位精度。

1 基于LS的UWB初次定位

本文UWB定位模型利用已知固定基站的坐标和测量所得移动节点与固定基站之间距离来进一步计算得到未知移动节点的坐标。UWB定位模型中共有四个固定基站节点和一个移动节点。

设置A、B、C、D四个基站的坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)、(x4,y4,z4),同时设置移动节点P的坐标为(xp,yp,zp),另外四个固定基站与移动节点之间的距离分别为d1、d2、d3、d4。

为保证在求解方程时,系数矩阵为非奇异矩阵,本模型按照对位基站处在同一水平高度,邻位基站处在不同水平高度分布,UWB定位模型,如图1所示。

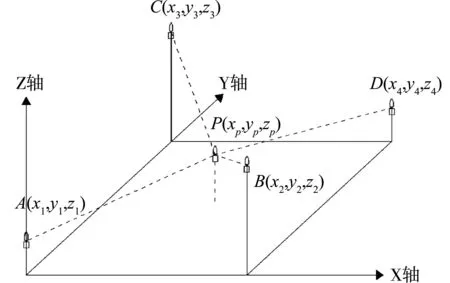
图1 室内UWB定位模型

由图1利用数学算法计算空间坐标可得:

(1)

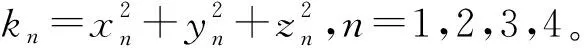
(2)

由相邻两式相减可得:

(3)

令式(3)中:

(4)

(5)

(6)

将式(4)—式(6)代入式(3)可转化为:

AX=B

(7)

设误差向量为δ,则有:

δ=AX-B

(8)

取δ无穷小时,X有最优解,令:

f=δ2=δTδ=(AX-B)T(AX-B)

(9)

对式(9)求导,令其结果为0可得:

(10)

因为AX=B有唯一解,所以有:

X=(ATA)-1ATB

(11)

由式(11)求解方程可得X,可得到移动节点坐标P(xp,yp,zp)。

2 算法与优化模型

2.1 支持向量机

支持向量机(Support Vector Machine,SVM)原本是一种非线性分类算法,SVM在非线性建模回归方面同样具有很多优势,它的目标主要是找一种拟合函数,以正确反映数据样本集变量之间的映射关系[8-10]。

定义回归拟合函数为:

f(xi)=wTxi+b

(12)

式(12)中,w表示输入样本xi的权向量,f(xi)为输出,b表示偏移量。假定高维空间中设给定样本集{data=(x,y),i=1,2,…,n},yi是每个xi对应的物理位置坐标。

定义线性不敏感损失函数为:

l[f(x),y,ε]

(13)

式(13)中,ε为不敏感系数,构造新的目标优化函数:

s.t.|yi-(wTxi+b)|≤ε,1,2,…,n

(14)

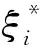
(15)

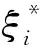
(16)

(17)

当数据为非线性训练数据时,优化目标函数就可通过核函数来表达,式(15)引入核函数K(xi,xj)就可转化为:

(18)

与之对应,回归函数相应变化为:

(19)

(20)

支持向量机回归结构特征主要是利用松弛变量并引入核函数技巧使得更多的样本符合约束条件来解决回归拟合问题。

2.2 改进秃鹰搜索算法

秃鹰搜索算法(Bald Eagle Search,BES),ALSATTAR.H.A等人[11]提出这是一种元启发式优化算法,该算法通过模拟秃鹰捕猎的行为,将其划分三个阶段,分别为选择、搜索和捕获。

选择阶段的秃鹰在飞行过程中,会选择最优目标区域。该选择阶段秃鹰更新的位置由随机搜索因数来确定,该数学模型为:

Pi,new=Pbest+αr(Pmean-Pi)

(21)

式(21)中,r为随机数,Pbest为秃鹰最优位置,Pmean为秃鹰的平均分布位置,Pi为随机第i只秃鹰的位置。

为了提升算法的优化效果,本文选择在BES算法的选择搜索阶段进行改进。

该算法假定秃鹰在搜索阶段中陷入了局部最优状态,进而影响秃鹰在全局搜索过程中无法捕猎,降低了该算法的优化效果[12-13]。李阳等人[14]提出随机游动(Random Walk,RW)利用混合交叉的方法产生新的解进而提高算法的局部搜索能力,从而减少局部寻优的时间,极大降低了陷入局部最优的风险。

彦苍等人[15-16]提出Levy飞行是常用的随机策略。在BES算法中引入Levy飞行模式,改进了原算法容易陷入局部最优缺点,从而提高总体的优化效果。引入式(21)后改为:

Pi,new=Pbest+α·r(Pmean-Pi)Levy+ε(Px-Py)

(22)

式(22)中,Px和Py为搜索空间中两只秃鹰随机搜索位置,ε是随机缩放因子。基于以上对算法的改进,现将新算法命名为LBES。

2.3 LBES-SVM模型

参数的优化选择对SVM的预测精度影响较大,而本文通过改进的LBES算法来寻优参数,能够有效地提高预测精度。

首先将LS算法初次定位后的移动节点坐标数据以及四个固定基站的坐标作为SVM模型的特征向量输入,且真实坐标作为标签;再通过数据处理将输入的数据集按照比例7:3划分训练和测试样本;训练部分先计算LBES算法的种群个体的适应度值,然后开始进行SVM模型训练;另外训练中通过LBES算法来寻找SVM最优参数,从而得到最优训练模型;接着将划分的测试样本输入到上述训练阶段所得的最优训练模型中进行回归预测;最后将其可视化并与标签作对比输出结果,具体模型流程,如图2所示。

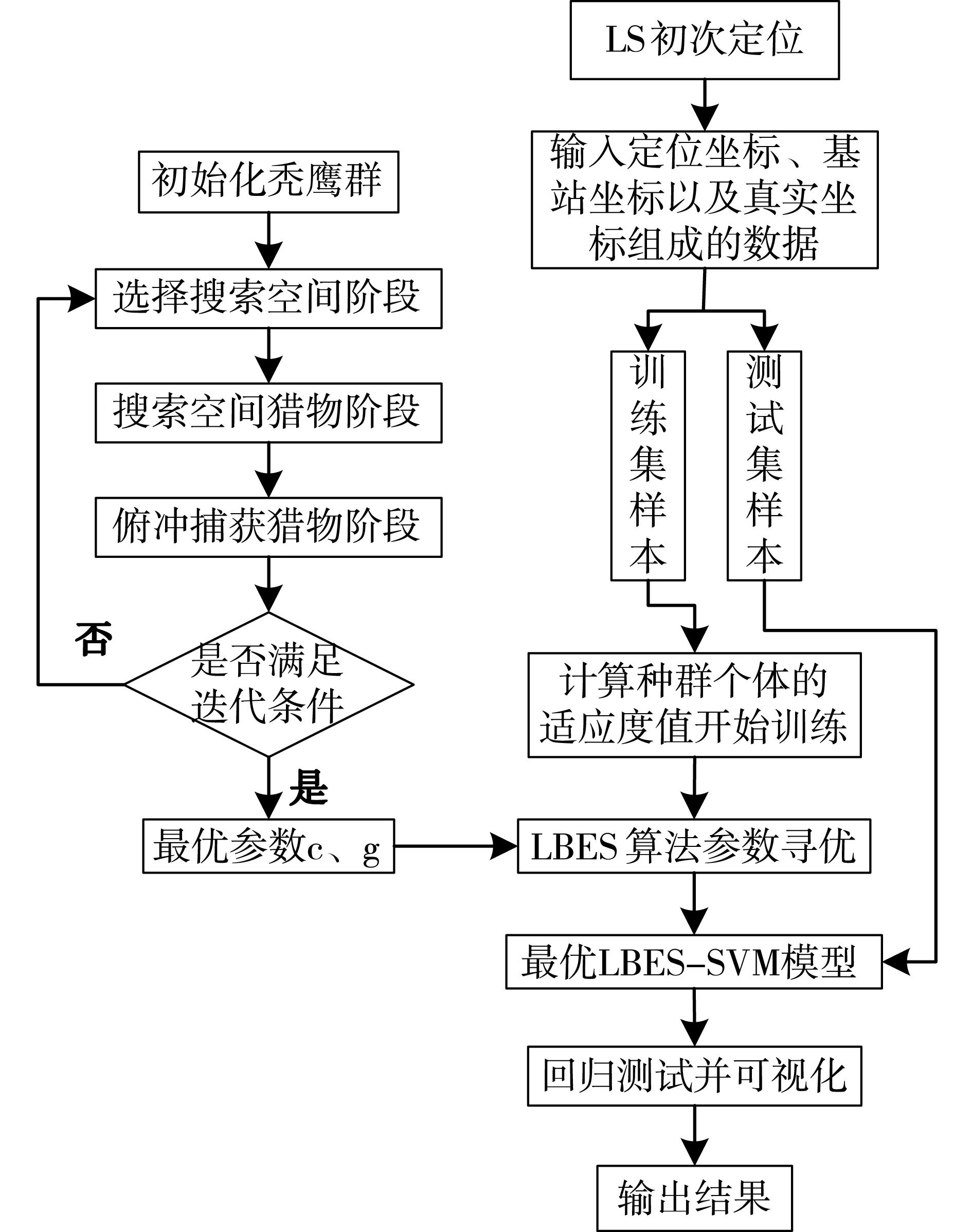
图2 基于LBES-SVM模型的坐标误差修正流程

3 UWB室内定位实验设计

3.1 实验仪器设备

利用DW传感器与STM32单片机制作了UWB的定位系统。本文的设备包括一个移动节点、四个基站、石制屏蔽罩、电脑作为上位机来采集数据。

3.2 实验设计

为模拟室内非视距环境,选择在一处正方形且较为封闭的室内场地进行实验。在测试场地中将A、B、C、D四个基站分别放置场地的四个角落处,形成长6m、宽6m、高3m的测试场地。设主基站对应的地面点为坐标原点,A到B方向为X轴,A到C方向为Y轴,垂直方向为Z轴。各基站坐标为:A基站(0,0,44.5),B基站(600,0,300),C基站(0,600,300),D基站(600,600,44.5)。为模拟受干扰情况的场景,利用石制屏蔽罩盖住移动节点并将屏蔽罩内空隙用砂粒填充。

3.3 数据采集

移动节点在四个基站形成的矩形区域内的位置采集数据,在每个位置停留一定时间,在该位置上采集足够多的数据,并记录该位置的真实坐标。本次实验的UWB设备在同一位置接收一段时间的数据,会导致所接收的数据出现大量相似或相同情况。因此需要清理相似或相同的数据,留下具有代表性的数据。

主基站在一个时刻会接收到其它三个基站发送过来的信息,包含该时刻下另外三个基站与移动节点的直线距离。同一时刻主基站上传至上位机时的数据包括四个属性,这四个属性的含义为四个基站与移动节点的直线距离。实验场景(单位:cm),如图3所示。

图3 实验测量场景图

4 测试结果及分析

向模型中输入初次定位坐标的数据后,设置两种算法的迭代次数均为100次,以均方误差值(MSE)为目标函数构建平均适应度曲线图。根据测量的所有的点数据,由于有多个点,算法得到多条曲线,将所有条曲线取均值,合成一条均值迭代曲线。同时根据平均适应度值与最佳适应度值作对比来观察比较算法优化前后的差异。BES-SVM算法和优化后的LBES-SVM算法的X、Y、Z三轴的平均适应度迭代曲线分别,如图4和图5所示。

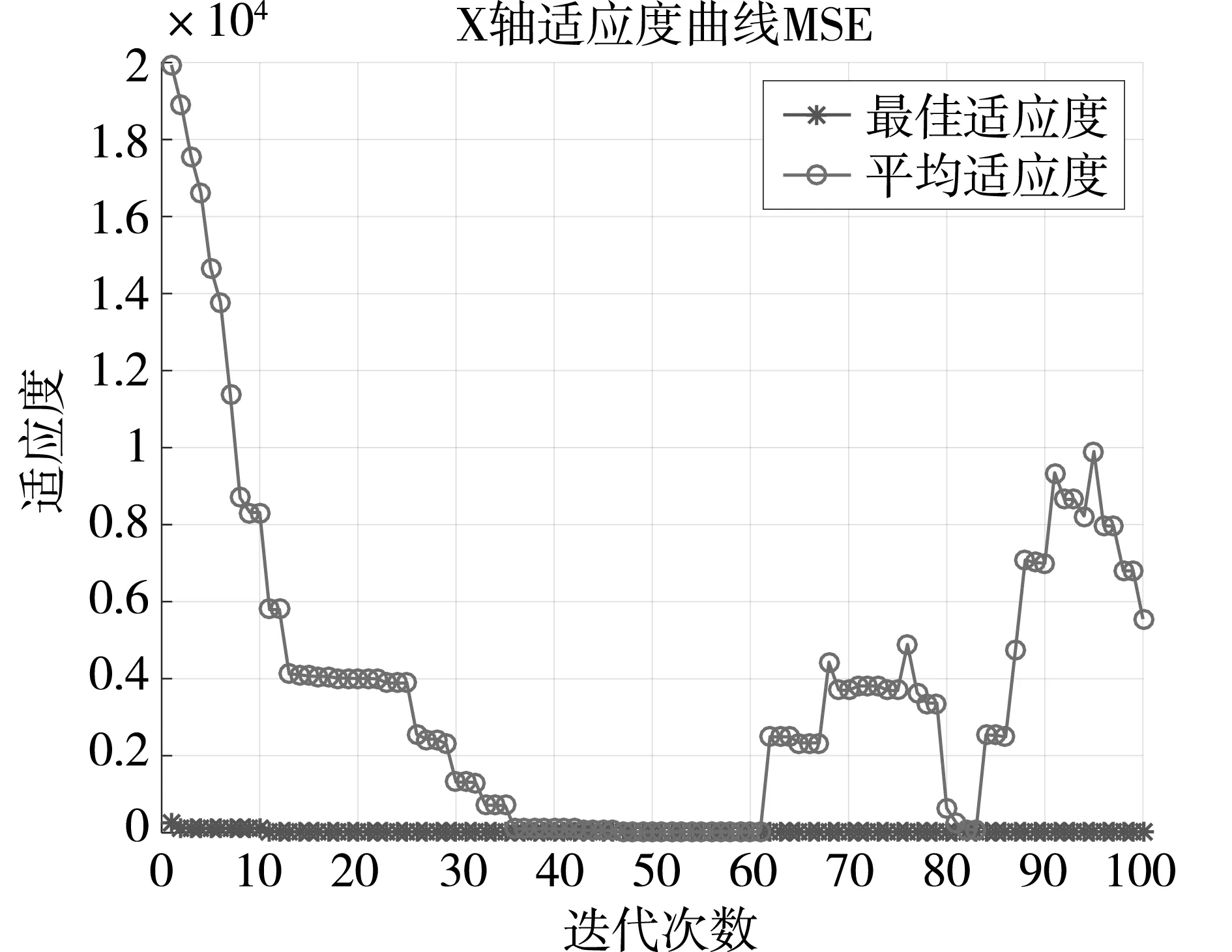
(a)x轴

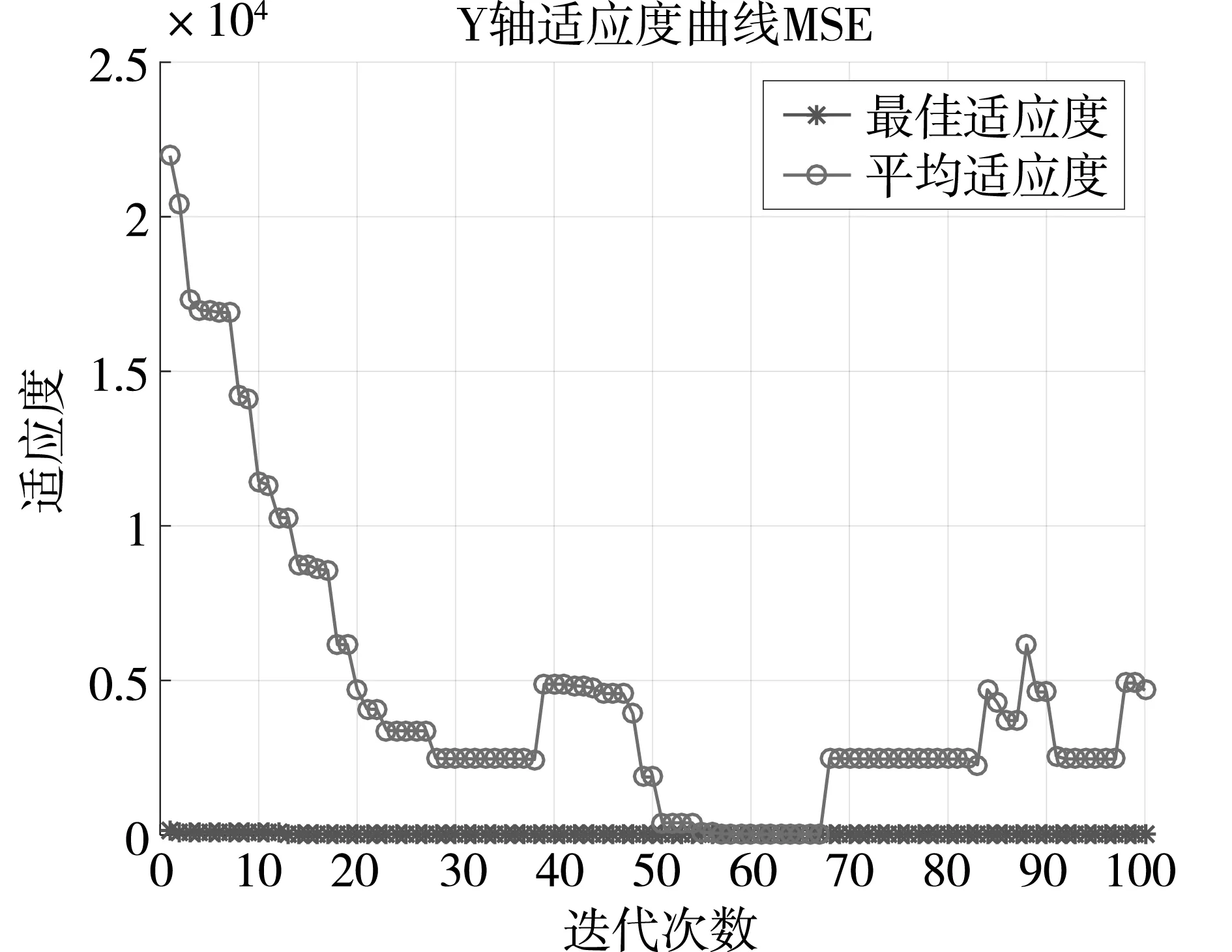
(b)y轴

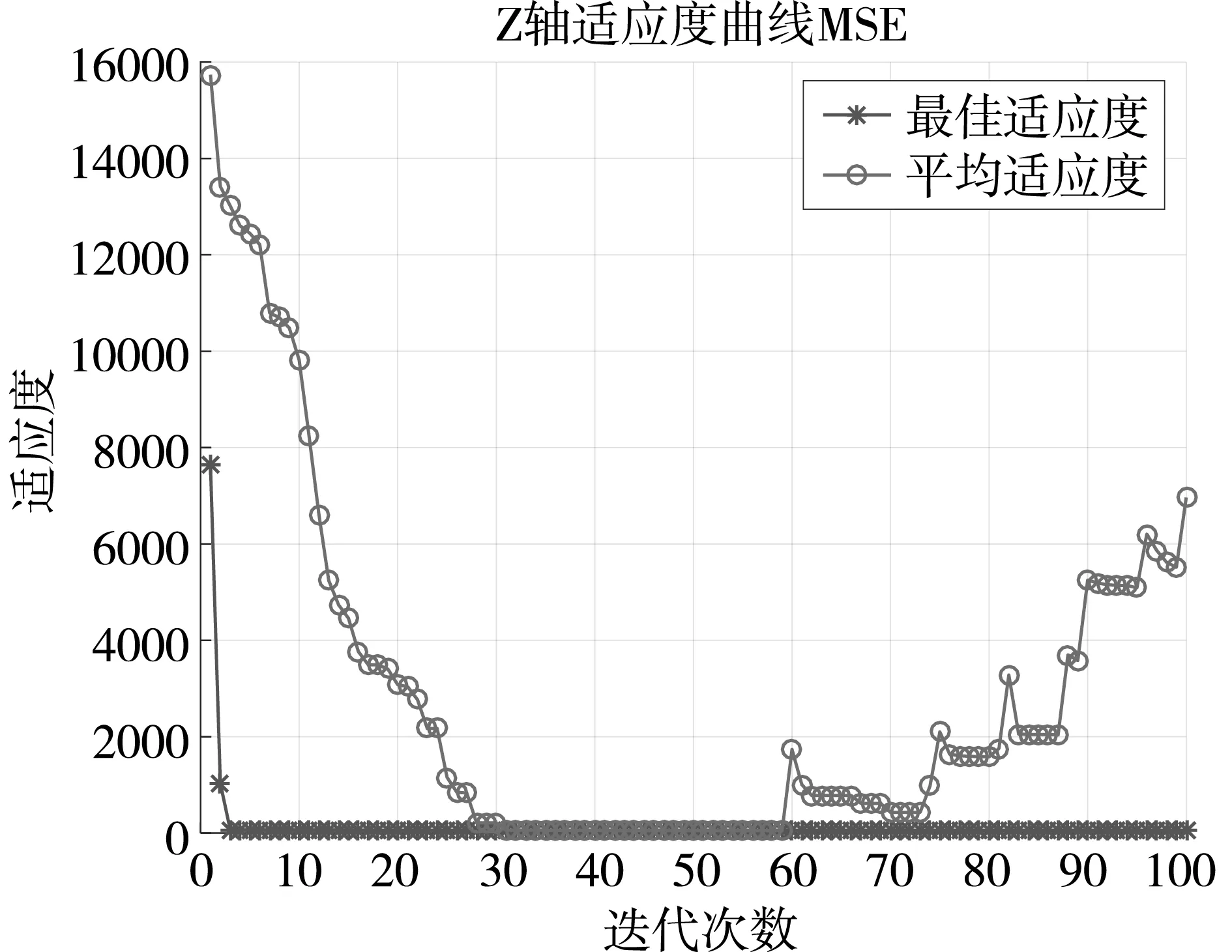
(c)z轴图4 BES-SVM算法三轴的平均适应度迭代曲线图

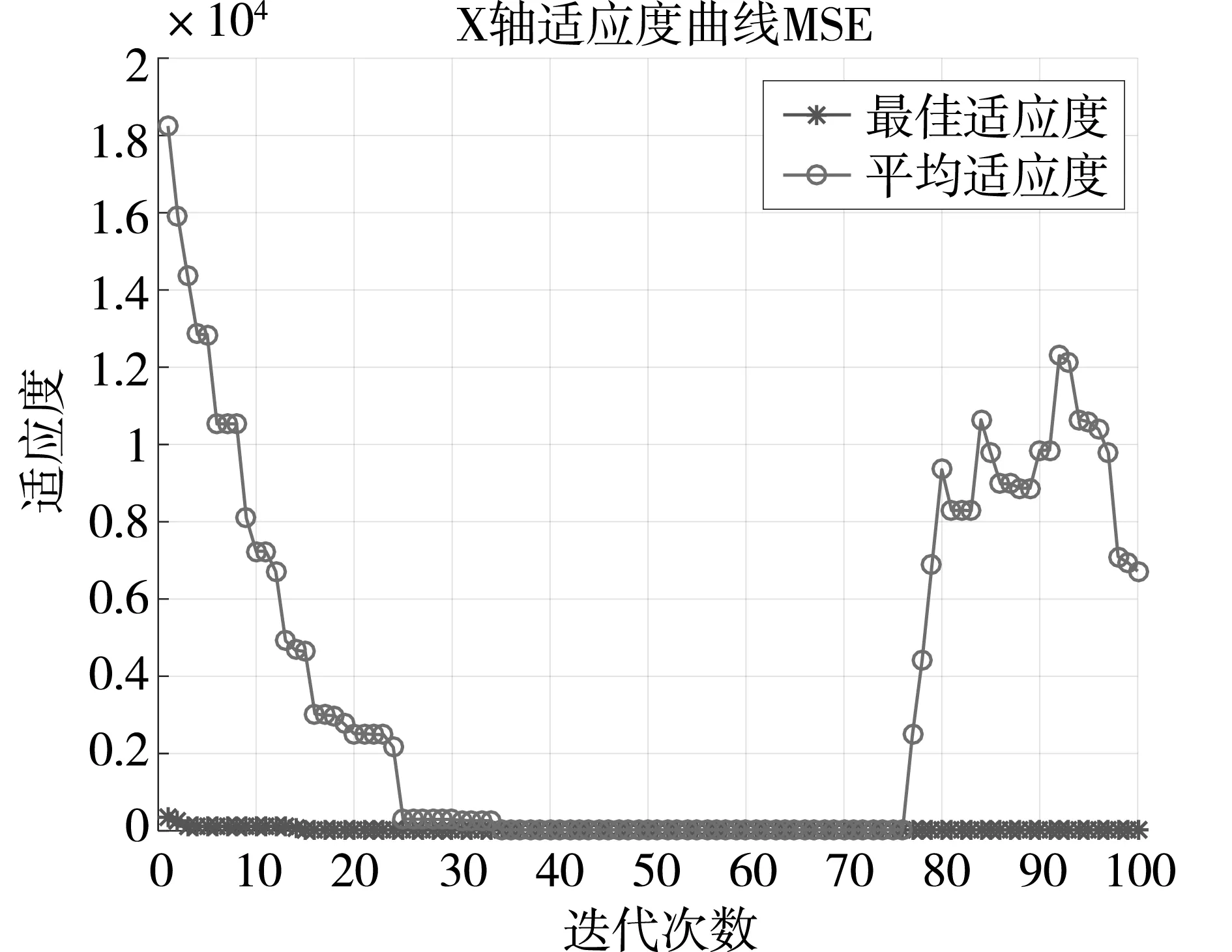
(a)x轴

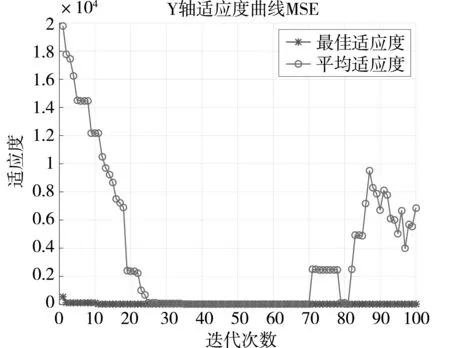
(b)y轴

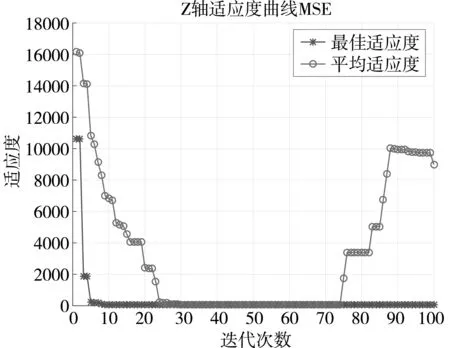
(c)z轴图5 LBES-SVM算法三轴的平均适应度迭代曲线图

由图4和图5对比可知,图5中X、Y、Z三轴的平均适应度曲线与最佳适应度曲线重合部分比图4的中更多,LBES-SVM算法计算出的均方误差值比BES-SVM算法计算出来的更小,即新的优化算法LBES-SVM成功地减小了误差,并且效果优于旧的算法,最终提高了系统的定位精度。

设置两种算法秃鹰种群数量为50,迭代次数为100,以欧式空间平均距离(Distance)和误差值(Error)构建目标适应度函数开始测试训练。对比的两种算法均利用优化SVM模型进行回归测试,并将空间坐标可视化。最后将优化算法修正后的坐标、初次LS定位的坐标及真实坐标作同一空间的对比。BES-SVM算法和LBES-SVM算法的处理结果分别如图6所示。

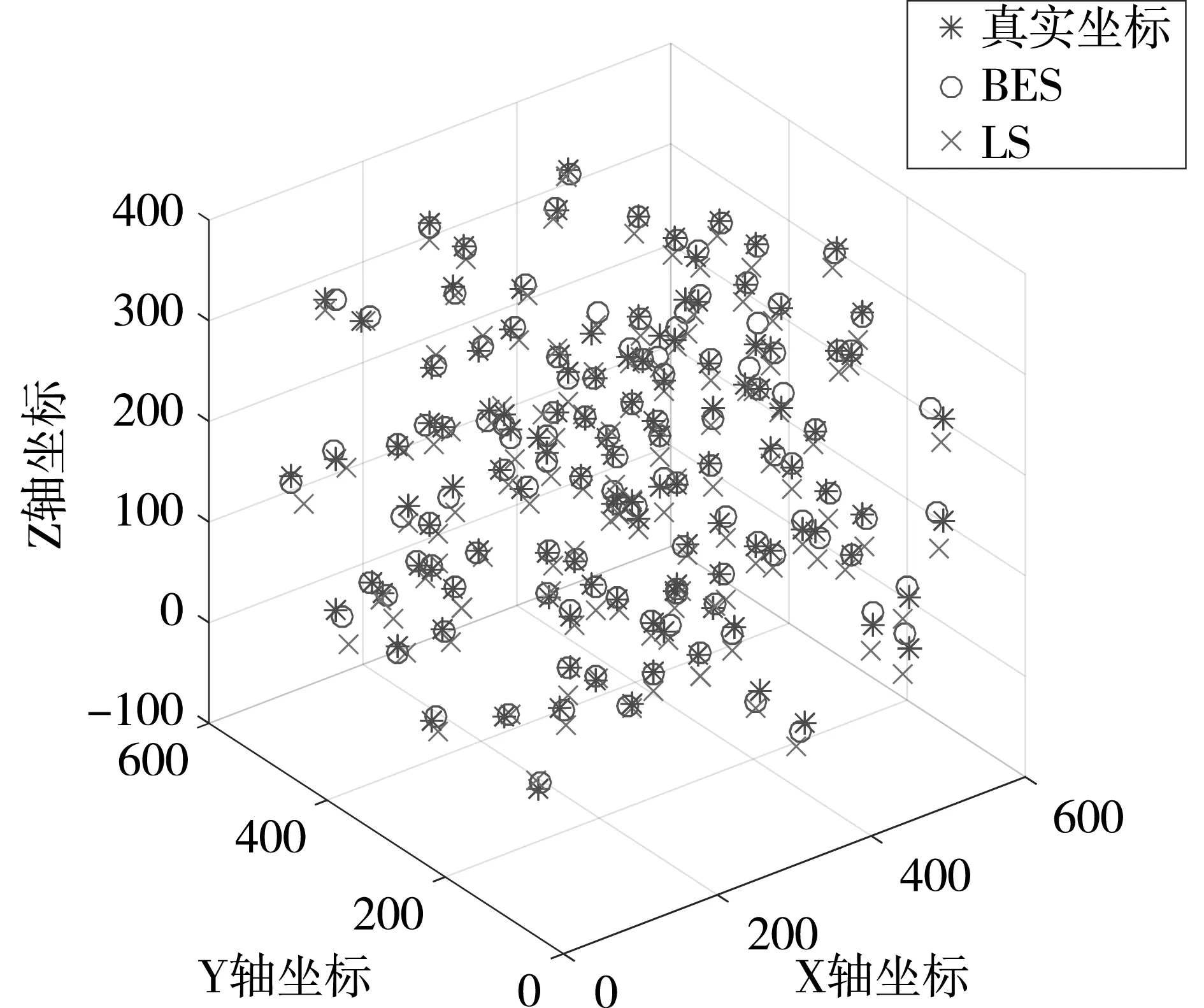
(a)修正前

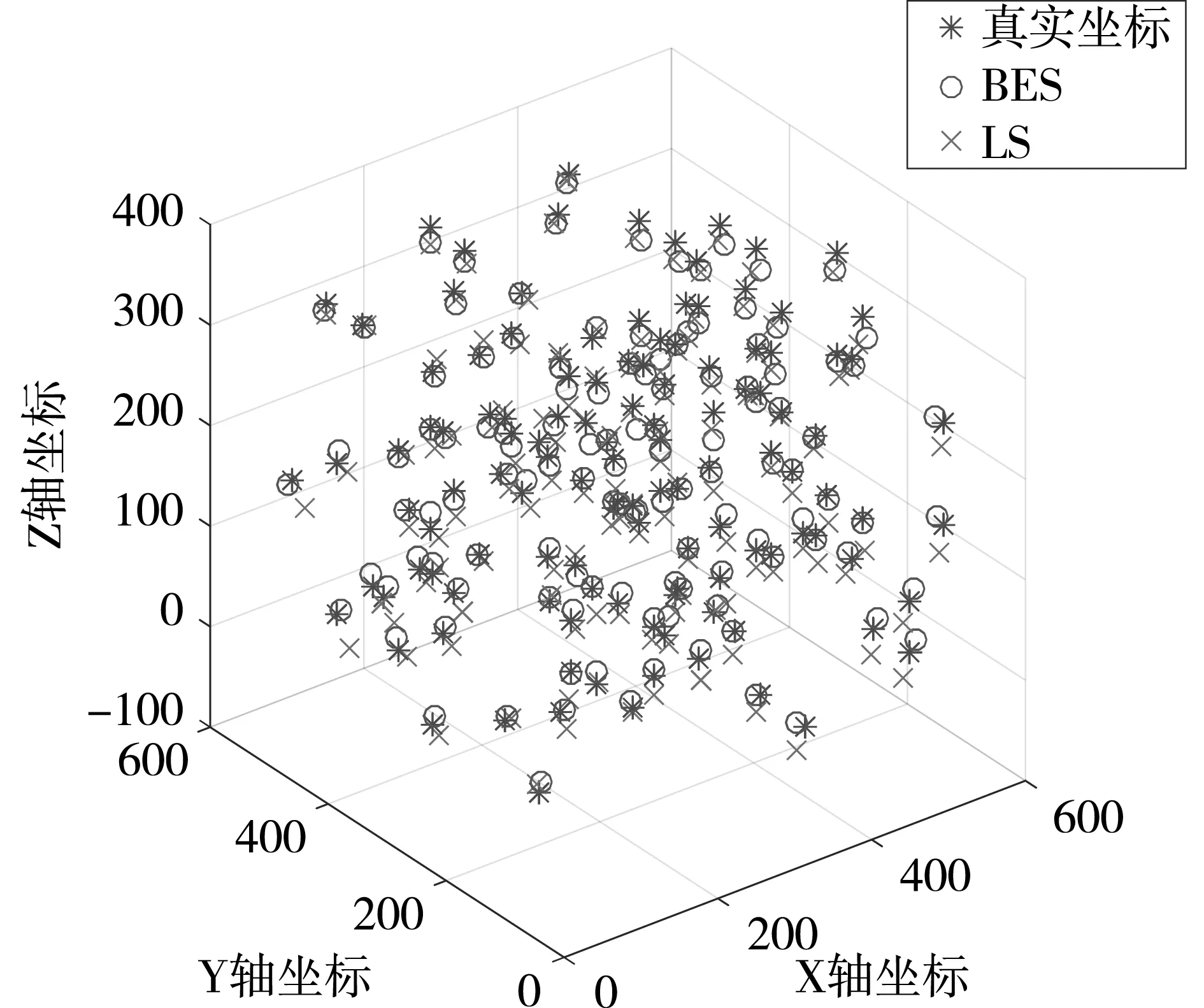
(b)修正后图6 坐标修正前后对比图

由图6可知,两种算法相对于LS初次定位的X、Y、Z轴坐标误差均有明显减少,即两种算法修正后的坐标相对于LS算法更接近于真实坐标,Z轴上的修正效果最佳。同时LBES-SVM算法修正后的空间坐标相对于BES-SVM算法修正的坐标更加接近于真实坐标,即LBES-SVM算法的误差修正效果更优。

上述两种算法模型测试训练的输出结果对应的参数指标X、Y、Z三轴的误差和欧式空间平均距离分别如表1和表2所示。

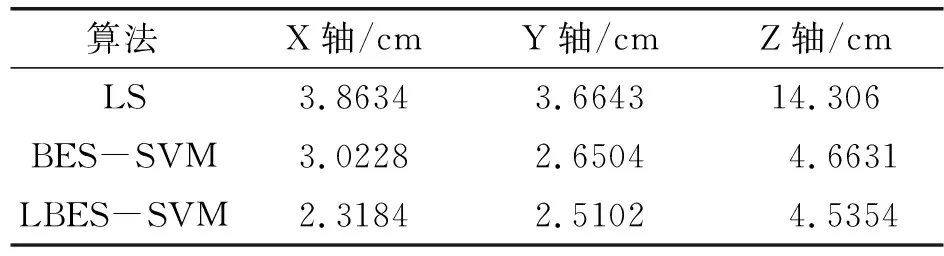
表1 误差对比

表2 欧式平均距离对比

由表1可知两种算法修正LS后的坐标在X、Y、Z三轴的误差上均有减小,且LBES-SVM修正效果优于BES-SVM,其中Z轴上的效果最佳,误差从14.3cm减少至4.5cm。

表2中Distance为修正后的定位坐标与真实坐标之间的欧式平均距离,数据显示两种算法的Distance分别由16.0cm减小至7.1cm和6.7cm。即修正后的距离明显减小,修正后的定位坐标更接近于真实坐标,且LBES-SVM算法的修正效果更优。

结语

为解决传统算法在非视距环境下UWB受干扰较为严重无法精确定位的问题,本文提出一种基于LBES-SVM的UWB室内定位算法,并进行了相关实验与测试。结果表明,LBES-SVM算法模型对LS算法初次定位的坐标有明显的修正作用,且效果优于传统定位算法。减少了NLOS环境引起的测距误差,提高了UWB室内定位的精度。在后续工作中,将继续研究在多种室内场景下的复杂定位,进一步提高算法的适应性、鲁棒性和应用价值。