变电站外短路时架空地线分流系数的计算方法
2023-06-14鲁志伟林忠宣
鲁志伟,董 威,冷 赫,林忠宣
(东北电力大学电气工程学院,吉林 吉林 132012)
0 引 言
变电站短路时故障电流的分布情况对电力系统接地设计至关重要,最严重的接地故障就是指暂态入地电流最大的情况,因此有必要引入分流系数对电流分布进行计算分析[1-4]。地网分流系数是指流经接地网的电流与流入变电站中性点的总电流比值,是研究地电位升、网孔电压、接触电压与跨步电压的基础[5-8]。国标GB/T 50065-2011《交流电气装置的接地设计规范》规定:在电力系统中一般情况下R≤2 000/IG其中R表示有效接地系统接地阻抗,IG表示入地故障电流[9]。由此可见合理的分流系数计算方法在接地系统设计中的重要性。
目前对于分流系数的计算方法主要有简易公式法和数值计算法,前者计算模型简单,但计算精度难以保证[10-11];后者计算模型复杂,考虑因素全面,计算结果更为准确[12-14]。对于数值计算法又以加拿大的F.Dawalibi博士提出的相分量法最具代表性,提出了以相分量模型为基础的广义双侧消去法,对CDEGS中变压器模型的搭建原理进行了系统介绍,用一个具有自感与互感的多导体终端代替了变压器模型,并在GD-SEM中使用了该模型,为后续研究提供了重要参考[15-16]。文献[17]基于广义双侧消去法,提出了可以自由选择故障类型与故障点数目的计算模型,可用于分析不同电气结构的互联系统。文献[18]将传统相分量法与变压器相分量模型结合,实现了多回输电线路的变电站发生接地短路时故障电流分布与地网分流系数的计算方法,并开发了计算分流系数的软件。文献[19]提出了一种可用于不同电压等级的复杂电力系统模型分流系数分析方法,推导并拓展了基于相分量的变压器导纳模型。文献[20]基于图论的思想,实现了多电源供电变电站短路时架空地线分流系数的计算方法。
虽然国内外已有大量文献对分流系数进行了研究,但由于大部分研究只关注了站内短路的情况,对于站外短路下分流系数的计算方法仍然缺乏深入研究。对于一些远距离送电的电站例如发电厂来说,其最大入地短路电流的故障点经常位于站外,所以合理的站外短路分流系数模型分析仍有现实意义。
基于以上研究,本文结合站外短路时的分流阻抗模型,得出了简化的站外短路时的分流阻抗电路,在此基础上,提出了一种基于回路电流法的站外短路分流系数计算方法,推导得出了地网分流系数的计算公式,将本文计算结果与CDEGS进行比较,验证了本文结果的正确性,并对影响站外短路分流系数的因素进行分析,提出了减小地网分流系数的措施。
1 站外短路时短路电流分布
如图1所示的短路电流分布图,假定在第s基杆塔发生了单相接地短路故障,当短路发生时从短路点产生的短路电流向两侧的架空避雷线流动,并通过各个杆塔的接地系统流入大地。从图1可以看出架空避雷线处产生的短路电流Imax可以分为两部分:一部分短路电流Ik被短路点前侧架空避雷线分流并返回中性点;另一部分短路电流Ip被短路点后侧架空避雷线分流并返回中性点。其中被前侧架空避雷线分流的电流又可以分:经各基杆塔逐级流入大地,再通过大地流入前侧变电站接地网,最后流回变电站中性点的电流ID;经各基杆塔分流后,剩余电流通过架空避雷线流入接地网,再流回变电站中性点的电流Iw。
根据上文描述的短路电流分布情况可得前侧变电站的电流分布关系,即
In=Iw+ID
(1)
定义站外短路时架空地线的分流系数为流经架空地线返回变电站的电流与流入前侧变电站中性点的总电流之比,用Ks表示,即
(2)
则经过大地流入变电站接地网的电流
ID=In(1-Ks)。

图1 站外单相短路时短路电流分布模型Fig.1 Short-circuit current distribution model of single-phase short-circuit outside the station
2 站外短路时等效阻抗模型及计算公式推导
2.1 变电站外短路时架空地线分流等效模型
假设架空避雷线与相线在第s基杆塔间发生绝缘击穿,即在变电站外发生单相接地短路故障,可将图1的站外短路电流分布系统模型等效成如图2所示的避雷线电路等效分流模型。图2中将架空地线分成n+1段,第1段左侧为靠近故障侧变电站,第n+1段为对侧变电站,故障发生在靠近第s段的杆塔处。

2.2 架空地线等效模型的去耦分析
当变电站外发生短路故障时,任意两处杆塔间的避雷线会与其相连的杆塔以及相邻的大地形成一个回路,这时短路电流将会在架空避雷线上产生感应电压,从而形成感应电流通路,因此在建立架空避雷线的等效模型的同时也应该考虑故障相与架空避雷线之间的耦合关系。如图3所示为第s个网孔的等值电路模型图,该模型包含了第s个网孔的自阻抗与互阻抗两个部分。
图3中,Rbs为相线的自电阻;Xbs为相线的自电抗;Rps为架空避雷线的自电阻;Xps为架空避雷线的自电抗;Zms为架空避雷线与相线间的互阻抗;Rs、Rs+1分别为第s个网孔两侧杆塔的接地电阻。
架空避雷线的自阻抗Zps及架空避雷线与相线之间互阻抗Zms的求取公式分别为[21-22]
(3)

图2 变电站外短路时避雷线分流等效模型Fig.2 Equivalent shunt model of lightning arrester line in case of external short circuit in substation
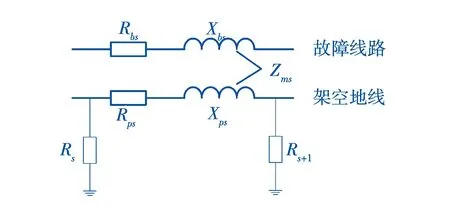
图3 单个网孔等效电路模型Fig.3 Equivalent circuit model of a single mesh
(4)
(5)
公式中:Rps为单位长度架空地线的自电阻,Ω/km;n为架空地线的根数;am为等价架空地线的几何平均半径,m;Lav为线路的平均档距,m;ρav为土壤的平均电阻率,Ω·m;f为工频,50 Hz;Dg为架空地线对大地的等价镜像距离,m;D1-2为架空避雷线对相线的几何平均距离,m。
其中对于单根与双根架空地线时D1-2分别为
(6)
(7)
公式中:Di-A、Di-B、Di-C分别为i根架空避雷线到第A、B、C相线的几何距离,m。
当在变电站发生单相接地短路时,会在故障相产生零序电流,零序电流在流动的过程中会在架空避雷线上感应出零序电压,此时可以将感应电压等效成一个电压源,感应电压分别为Em1、Em2、…、Emn、Em(n+1)。因为避雷线中的感应电压方向与故障相中产生的零序电流相反,所以感应电流对避雷线的分流起加强作用。以第s个网孔为例,结合图3中架空线路与导线间的耦合关系,得到去耦后的避雷线中的感应电压与零序电流的方向如图4所示。

图4 第S个网孔等效电压方向与短路电流流向Fig.4 Equivalent voltage direction and short circuit current direction of the S-th mesh
其中,Ems可表示为
Ems=3I0Zms
(8)
公式中:I0为流过故障相的零序短路电流;其中Zms可用公式(4)计算。
2.3 架空地线等效模型的简化
基于综上分析,结合图4中的去耦合的感应电压图,根据电路原理将等效电阻、电抗和架空避雷线的感应电压做进一步简化,同时将短路点等效成一个电流为Imax的并联电流源,即可得到图5中的分流阻抗模型。

图5 站外短路时等效电路模型Fig.5 Equivalent circuit model for short circuit outside
图5中,Zp1…Zps…Zpn、Zp(n+1)分别为考虑零序阻抗后的避雷线等效阻抗。
为了方便计算继续对图5的模型进行等效分析,由文献[23]可知短路点距离变电站越近,从短路点返回系统中性点的电流越大,因此本文假设故障发生在靠近变电站的第1基杆塔处,由戴维南等效定理可对图5中的电流源与电阻并联的部分进行等效,等效后电压源数值为ImaxR1,等效电路图如图6所示。

图6 简化的站外短路时等效电路模型Fig.6 Simplified equivalent circuit model for short
2.4 变电站外短路时架空地线分流系数
由图6可知,流入前侧变电站中性点的电流为
(9)
公式中:Z′为短路点前侧的等效阻抗;Z″为短路点后侧的等效阻抗。Z′、Z″的数值可用公式(10)和公式(11)进行计算。

(10)


(11)
此时由公式(2)可知,只需求出Iw即可求得站外短路分流系数Ks,采用电路理论中的回路电流法对Iw进行求解,并做出图6中电路图的等效树图,结果如图7所示[24]。

图7 站外短路时阻抗模型的等效树图Fig.7 Equivalent tree diagram of impedance model for short circuit outside the station
图7中树图共包含n基杆塔。其中,0表示参考节点大地,树枝1为故障侧变电站接地网的等效支路,树枝3为包含故障点的杆塔和接地电阻等效支路,支路5、…、2n-1、2n+1、2n+3分别为各基杆塔与接地电阻等效支路且为树枝;支路2、4、…、2n、2n+2分别为各段架空地线等效支路且为连枝。显然树枝1电流的大小即为Iw,根据图7可列写(n+1)×(2n+3)阶的基本回路矩阵Bf为
(12)
支路阻抗矩阵为Zp为对角矩阵,阶数为(2n+3)×(2n+3)阶,可用公式(13)表示为
Zp=diag[Rd,Zp1,R1,Zp2,R2,…,Zpn,Rn,Zp(n+1),
R(n+1)]
(13)
回路电流矩阵Il为(n+1)×1阶矩阵,可表示为
(14)
公式中:I1,I2,…,In,I(n+1)为各网孔的回路电流。
由图6可得,电压源矩阵为(2n+3)×1阶矩阵,可用Us表示为
Us=[InRdEm1ImaxR1Em20 …Emn0
Em(n+1)0]
(15)
其中,Ems可由公式(8)计算出结果。
由回路电流法得
(16)
解上述方程可得回路电流的矩阵形式为
(17)
显然Iw=-Il(1,1),因此可得避雷线分流系数计算公式为
(18)
由上述公式可得到站外单相短路时的分流系数,考虑到计算的复杂性,本文采用Mathematica软件实现求解过程。
3 计算方法的对比验证与影响因素分析
3.1 对比验证
为对计算方法进行验证,针对同一模型分别采用本文提出的算法与相关商业软件CDEGS中的SPLITS模块进行计算。以某110 kV变电站为例,假设在靠近变电站处第1基杆塔发生单相接地短路故障,取靠近故障侧变电站接地电阻为0.4 Ω,杆塔档数为16基,档距取400 m,杆塔接地电阻为10 Ω,相线位置参数为(-7,11)m;(0,11)m;(7,11)m,架空地线位置参数为(-6,18)m;(6,18)m,架空地线的型号为GJ-80。
其他参数保持不变,分别采用GJ-35、GJ-80、LGJ-35/6、OPGW型避雷线时对地网分流系数进行计算,本文计算结果与CDEGS计算结果及相对误差如表1所示,计算结果显示计算误差保持在10%以内,满足工程计算精度要求,可为实际工程设计提供参考。
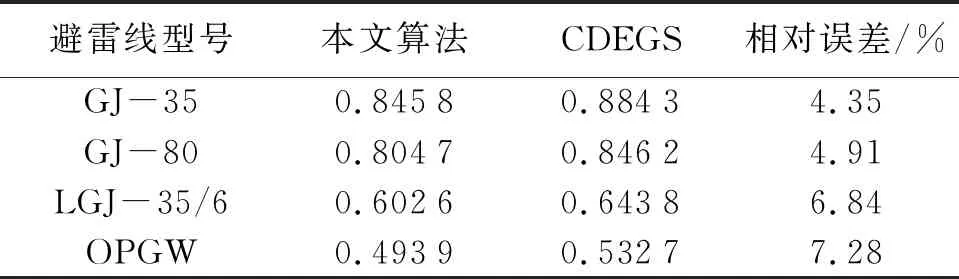
表1 地网分流系数计算结果对比与相对误差
3.2 影响因素分析
1)变电站接地电阻及避雷线类型对分流系数的影响
由于变电站接地电阻的变化会改变系统中的电流分布,从而对分流系数产生影响。分别取变电站接地电阻Rd=0.1~1.0 Ω,架空地线型号取GJ-35、GJ-80、LGJ-35/6、OPGW,其他条件不变时分流系数Ks变化情况如图8所示。随着变电站接地电阻Rd增大,地网分流系数Ks逐渐减小,此时由变电站流入地网的故障电流减小,这是因为随着Rd增大,导致流入避雷线-杆塔系统的故障电流增大。且计算表明当变电站接地电阻从0.5 Ω升高到0.6 Ω时,地电位升升高了17.1%。另外,结合图8与表1能够发现架空地线导电性越好,地网的分流系数越小,流入架空地线的故障电流也就越大。为减小入地短路电流,可采用导电性能更好的避雷线来增加避雷线的分流能力。

图8 变电站接地电阻及避雷线型号对分流系数的影响Fig.8 Influence of grounding resistance and type of lightning arrester on shunt coefficient
2)杆塔接地电阻对分流系数的影响
随着杆塔接地电阻的变化,避雷线-杆塔系统的整体阻抗也会改变,因此会对地网分流系数产生影响。计算杆塔接地电阻Rs=5~30 Ω时的分流系数,计算结果如图9所示。从图9可以看出,当杆塔接地电阻Rs逐渐增大时,地网分流系数Ks也随之增大,但当杆塔电阻增大到16 Ω时,分流系数增加趋势逐渐减小。另外将前5基杆塔接地电阻改为10 Ω其余杆塔接地电阻保持20 Ω不变与杆塔接地电阻皆为20 Ω时相比地网分流系数减小了2.7%,由此可见进线段杆塔接地电阻对地网分流系数的影响最为明显。因此在设计避雷线-杆塔系统时,可优先降低变电站进线段的杆塔接地电阻,从而增加架空地线的分流效果。
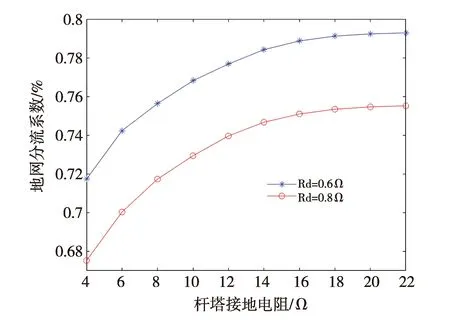
图9 杆塔接地电阻对分流系数的影响Fig.9 Influence of tower grounding resistance on shunt coefficient
3)杆塔档数及杆塔档距对分流系数的影响
随着杆塔档数与档距增加,避雷线-杆塔系统的阻抗也随之增大,会对分流系数产生影响。现取杆塔档数n=1~25时分流系数变化情况如图10所示。由图10可知,当增加档数n时,地网分流系数也逐渐增大,且当档数增加到14~16时,档数的增加对分流系数几乎没有影响。另外,档距的增加也会使地网分流系数增大,且随着档距的增大其对分流系数的影响逐渐减小。这是因为档数或档距增大时,地线的总等效阻抗增大,导致入地故障电流增大。根据以上结论,在工程计算时可优先考虑前16基杆塔对分流系数的影响,计算结果就可满足实际工程需求。
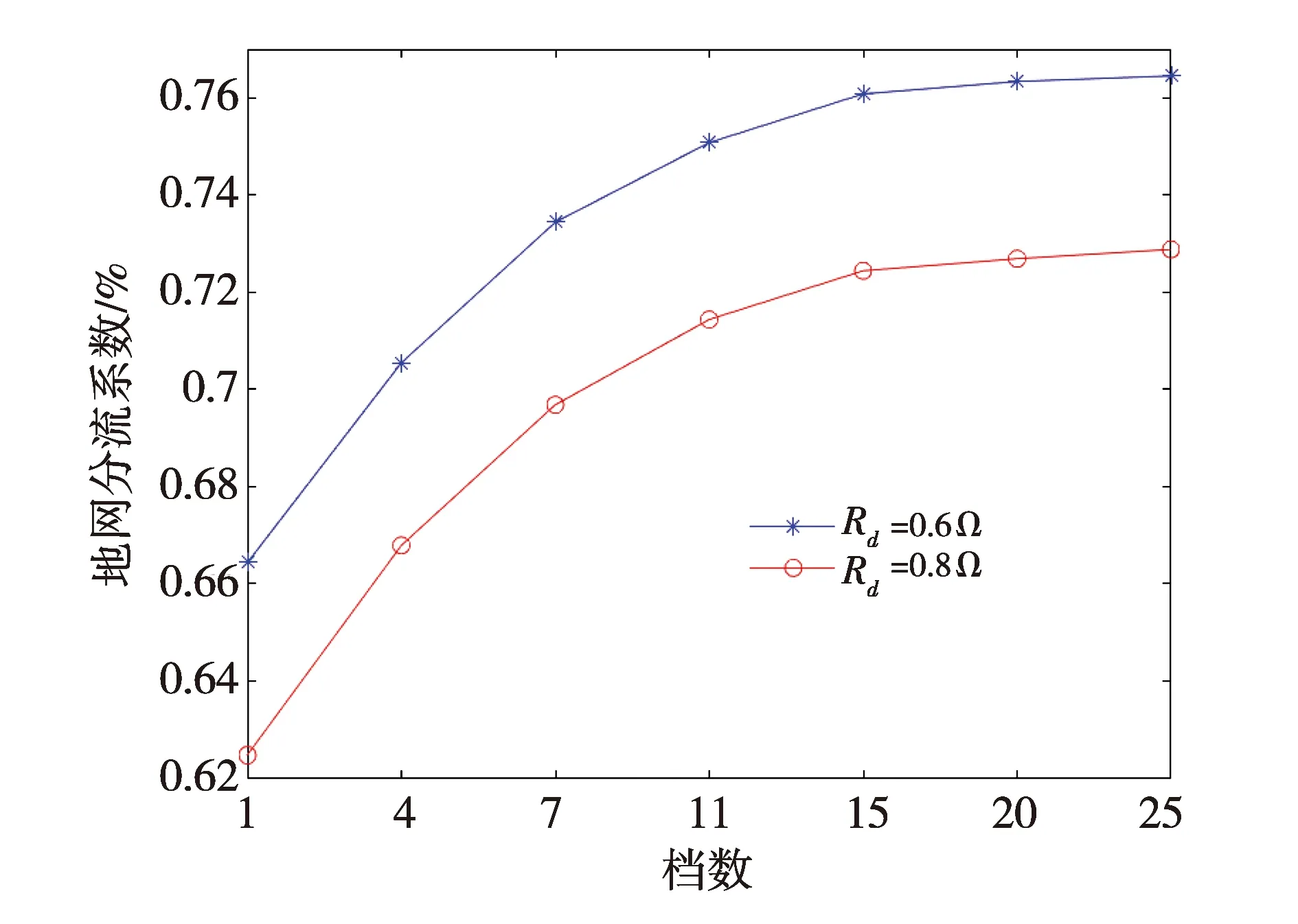
图10 杆塔档数对分流系数的影响Fig.10 Influence of the number of tower brackets on shunt coefficient
4 结 论
本文通过分析站外短路时的分流阻抗电路,结合回路电流法推导出了地网分流系数的计算公式,对变电站模型进行了计算分析,并对计算结果进行了验证。分析了变电站接地电阻、架空地线型号、杆塔电阻、档距与档数对地网分流系数的影响,最后提出了降低地网入地电流的合理性措施。主要有以下结论:
1)本文通过研究变电站外单相接地短路时的分流阻抗模型的同时考虑了零序电流分量与避雷线上的感应电压,结合回路电流法推导出站外短路时地网分流系数的计算公式。将本文算法与CDEGS进行比较分析,结果显示计算误差在10%以内,验证了本文算法的实用性。
2)通过影响因素分析发现变电站接地电阻减小会导致地网分流系数增大,架空地线类型、杆塔接地电阻以及杆塔档数与档距的变化都会导致地网分流系数的改变。且当影响因素达到饱和值时,地网分流系数会逐渐趋于稳定。
3)本文提出了降低地网分流系数的措施,为实际工程设计提供了参考。当变电站接地电阻值一定时,可通过适当降低靠近变电站杆塔接地电阻,增加避雷线-杆塔系统的分流能力。应尽量采用钢芯铝绞线等导电性较好的避雷线,避免使用钢绞线,可以有效的降低流入变电站地网的故障电流。
