基于O3KID-DMD方法的机电振荡参数在线辨识

王丽馨,沙东鹤,高 晗

(东北电力大学电气工程学院,吉林 吉林 132012)

0 引 言

随着电力系统的规模和复杂度不断增加,低频振荡问题仍然是制约输电线路传输能力、威胁电力系统安全稳定运行的关键问题[1-2]。因此,快速准确地获取低频振荡模态特征是有效抑制电力系统低频振荡的关键问题之一[3-6]。

近年来,广域量测系统的广泛应用为基于量测信息的机电振荡特征分析提供了新思路[7-8]。电力系统正常运行过程中,时刻存在负荷小幅随机波动、新能源有功间歇性输出等随机小幅随机扰动,此类随机小幅扰动作用下的系统随机响应信号时刻存在的,且蕴含丰富的电力系统机电振荡信息,能够反映系统正常运行时的小干扰稳定水平[9-12]。

近年来,基于随机响应信号的低频振荡模式辨识研究成果大量涌现。文献[13]首先证明了基于随机响应信号的机电振荡参数辨识的可行性。文献[14]和[15]分别采用随机子空间辨识技术和小波尺度分解技术提取机电振荡参数。文献[16]和[17]指出动态模式分解算法(Dynamic Mode Decomposition,DMD)是一种高效的机电特征参数提取技术,已广泛用于电力系统的机电特征分析。然而,该方法只能将脉冲响应作为输入,这在一定程度上限制了其应用。文献[18]将自然激励技术与DMD方法结合,自然激励技术可以从环境信号中提取自由响应,这使得DMD方法可以应用于随机响应数据辨识机电振荡参数。然而,自然激励技术中参考通道信号的选择对参数辨识的准确性有很大影响。

由Juang等人提出的观测器/卡尔曼滤波识别(OKID)算法是一种有效的时域识别技术,可以基于系统输入激励-输出响应提取系统的马尔可夫参数。该方法已广泛应用于振动模态分析和结构损伤检测方面[19]。然而,电力系统在正常运行时往往难以直接量测各设备输入信号,这使得O3KID技术在仅能获取量测输出响应信号的电力系统中应用困难。

本文提出了基于O3KID-DMD的电力系统机电振荡参数辨识方法,利用O3KID从多通道量测随机响应数据中获得系统脉冲响应,进而利用DMD方法提取系统机电振荡特征参数(振荡频率、阻尼比、模态振型及参与因子)。IEEE 16机仿真系统充分验证了本文方法在系统模式参数识别方面的可行性与优越性。

1 基于O3KID-DMD方法的机电特征参数辨识

卡尔曼滤波理论是基于一定的先验知识和当前时刻的量测数据采用滤波技术得到该时刻当前的状态值。本文通过引入观测矩阵,利用环境激励下量测的随机响应数据构建系统最优观测器,获得系统的马尔科夫参数(脉冲响应),进而依据得到的脉冲响应,采用动态模式分解方法提取系统机电振荡特征参数。

1.1 O3KID技术

本文O3KID技术在卡尔曼滤波理论基础上,通过引入观测器矩阵K构造电力系统最优观测器,以估计系统的实际状态

(1)

且满足:

(2)

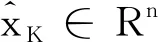
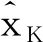
把公式(2)代入公式(1),观察器的状态方程和输出方程表达示为

(3)

公式中:Ad=Ad-KC。

将公式(3)在时间轴上向前移动p-1个时间步长(重复替换),然后将时间向后移动p个单位,为

(4)

公式中:

(5)

把公式(5)带入公式(3)中

yK=ΦvK+εK

(6)

包含观测器的脉冲响应。

公式(6)为仅利用系统量测输出响应构建的自回归模型,其中φ包含了观测器的脉冲响应,对应于离散时间线性系统的单位脉冲响应。公式(6)可以由测量数据的各时间步长K=p,p+1,…l-1表示为

Y=ΦV+E

(7)

公式中:

(8)

公式中:l为测量数据的长度。

公式(7)中矩阵Y和V可以通过广域量测获取。假设E是误差项,当测量数据的长度(l)和过去输出量测量的长度(p)满足:l-p>pm,即方程的个数多于未知数时,利用最小二乘法求解公式(7)可以得到观测器的马尔科夫参数(脉冲响应)为

Φ=YVT(VVT)-1=YV+

(9)

公式中:“+”表示矩阵的Morre-Penrose伪逆。

观测器马尔科夫参数与系统的脉冲响应满足

(10)

因此,基于公式(7)采用最小二乘方法有效估计观测器马尔科夫参数,进而根据获得的观测器马尔科夫参数利用公式(10)计算得到原系统的脉冲响应。

1.2 动态模式分解方法(DMD)

动态模式分解方法,是一种高维系统降阶算法,广泛应用于机械流体力学方面的分析,2015年由Barocio首次将其进入到电力系统机电振荡参数识别领域。下面对DMD的基本原理进行简要回顾。

电力系统的动态模型通常可以表示为

(11)

公式中:Δx(t)为测量得到的系统状态变量;Ad为离散系统的状态矩阵。

假设状态变量在时间tK时的第K个采样点为ΔxK=Δx(tK)。量测数据是一个由窗口间隔内的最新采样点组成的移动窗口,可以表示为

(12)

因此,系统的离散采样数据表达式[14]为

Xm+1=AdXm

(13)

通过对原始数据矩阵Xm进行奇异值分解得到模态U

Xm=U∑V*

(14)

公式中:U和V均为酉矩阵,且满足U*U=I,V*V=I;I是一个单位矩阵;∑为奇异值对角矩阵。

(15)

(16)

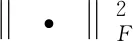
结合公式(14)～公式(16),可以得到

(17)

2 基于O3KID-DMD的机电特征参数提取

PMU能够同步记录系统不同空间位置的环境数据,并且随着PMU在电力系统中的广泛部署,以PMU为主体的电网广域测量系统为电力系统机电振荡特征参数的提取提供了有力的技术手段。PMU可以实时量测发电机及网络中的有功功率、频率、相角、母线电压等电气量,并经由WAMS将信息传递给电网调度控制中心。由负荷小幅波动等外部激励下的随机响应信号中包含了诸多系统的机电特征信息。本文以上传至电网运行控制中心的发电机随机响应信号为数据基础,通过O3KID-DMD方法实现机电振荡参数在线辨识。

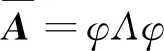
(18)

进一步将离散系统特征值λi转换为连续系统特征值ηi

ηi=log(λi)/Δt=αi+jβi

(19)

公式中:Δt为采样时间间隔。

因此,可以得到第i个模式对应的振荡频率fi和阻尼比σi

(20)

系统的模态振型矩阵φ

φ=[φ1,…φi,…,φn]

(21)

公式中:φi为第i个特征值对应的右特征向量。

参与因子pKi表示为

pKi=φKiφiK

(22)

公式中:φKi为右特征向量矩阵中的K行i列元素;φiK为左特征向量矩阵的i行K列元素。

基于广域量测随机响应信号,利用O3KID-DMD算法提取机电振荡特征参数的流程如图1所示,可以大致分为以下四步:

Step1 获取系统环境激励下的全部发电机有功功率、角频率作为输入信号。首先对信号进行预处理,将非重点关注的频段滤除。随后对电力系统的动态特性进行持续在线监测,判断系统是否发生持续性的低频振荡。根据监测结果选择不同的辨识方法对系统机电振荡参数进行提取。

Step2 若系统发生持续性低频振荡,则采用DMD方法或其它暂态振荡信号辨识方法提取系统的振荡模态参数。

Step3 若系统未发生明显低频振荡,则利用本文提出的O3KID-DMD方法在线提取包含振荡频率、阻尼比和模态振型在内机电小干扰稳定评估指标参数。

Step4 利用Step3中提取到的稳定评估指标参数进行机电稳定性分析,为系统的安全稳定运行提供指导。

图1 基于O3KID-DMD的小干扰稳定在线评估示意图Fig.1 Schematic diagram of online evaluation of small disturbance stability based on O3KID-DMD

3 算例仿真与案例研究

3.1 算例仿真分析

本节通过对IEEE 16机系统仿真分析,验证所提出的基于O3KID-DMD的机电特征参数提取方法的有效性。图2给出了经典IEEE 16机68节点互联系统结构图,系统的详细结构参数参见文献[20]。在MATLAB提供的电力系统工具箱(Power System Toolbox,PST)仿真平台上搭建系统并进行后续仿真分析验证。

基础运行方式下,在系统稳定平衡点处线性化,得到系统状态空间矩阵,并对其进行特征值分解计算系统机电小干扰特征参数。机电小干扰稳定分析结果(Small Signal Stability Analysis,SSSA)表明系统包含11个为局部振荡模式,4个为区域间振荡模式。通常,由于区域间模式影响范围较广,且极易演化为弱阻尼低频振荡,故本节以下主要针对系统的四个区域间模式进行深入分析。该系统四个区域间模式的振荡特征参数结果如表1所示。

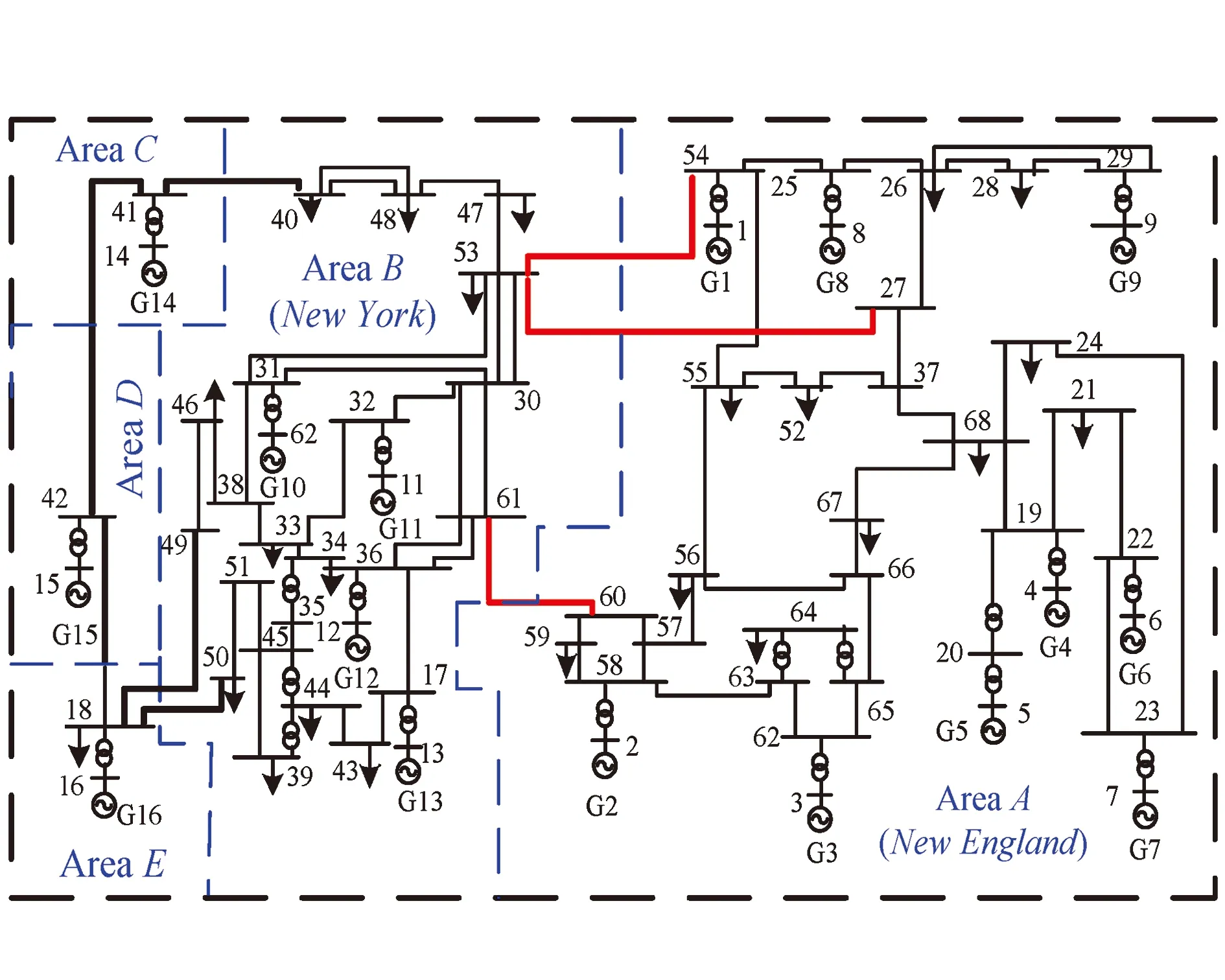
图2 16机系统结构图Fig.2 16 machine system structure diagram

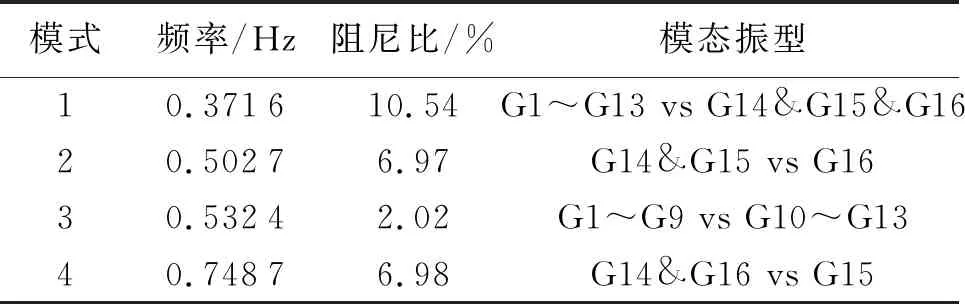
表1 16机系统小干扰稳定计算结果

为了模拟系统正常运行过程中,由于负荷随机波动、新能源有功间歇性输出等随机小幅值随机激励,本节假设系统全部负荷以基础值的5%随机波动,即基于PST仿真平台,各次仿真步长下,在系统中全部33处负荷的基础值上叠加高斯白噪声序列,且波动序列标准差为负荷基准值的5%。

获取系统连续10 min的全部发电机的角频率、发电机功角以及发电机出口有功功率随机响应,并以此为本文O3KID-DMD算法输入,算例分析在处理器主频2.0 GHz,内存16 GB的计算机上开展,本文所提方法在MATLAB平台上编程实现。为减少随机响应的随机性引起单点模式辨识结果的不确定性,本节采用滑动窗的方式进行机电振荡参数提取。滑动分析窗口选择为2 min(12 000个采样点),每2 s滑动一次分析窗口,对10 min内辨识得到的系统4个区域间振荡模式对应的振荡频率和阻尼比结果进行统计分析,并将辨识结果与NExT-DMD方法的辨识结果和SSSA计算结果进行对比,结果如表2所示。

分析表2中机电振荡参数统计结果可以看出,利用本文方法辨识得到的振荡频率和阻尼比结果统计均值与基础运行方式下小干扰稳定分析结果一致,且标准差较小,表明辨识结果以均值为中心集中分布。此外,与NExT-DMD方法辨识结果对比可以看出,本文所提方法的振荡参数辨识结果的统计均值与标准差普遍小于NExT-DMD方法的辨识结果,这种现象对于强阻尼模式更加明显,说明本文所提方法在机电振荡特征参数提取方面具有更高的可靠性和精确性。

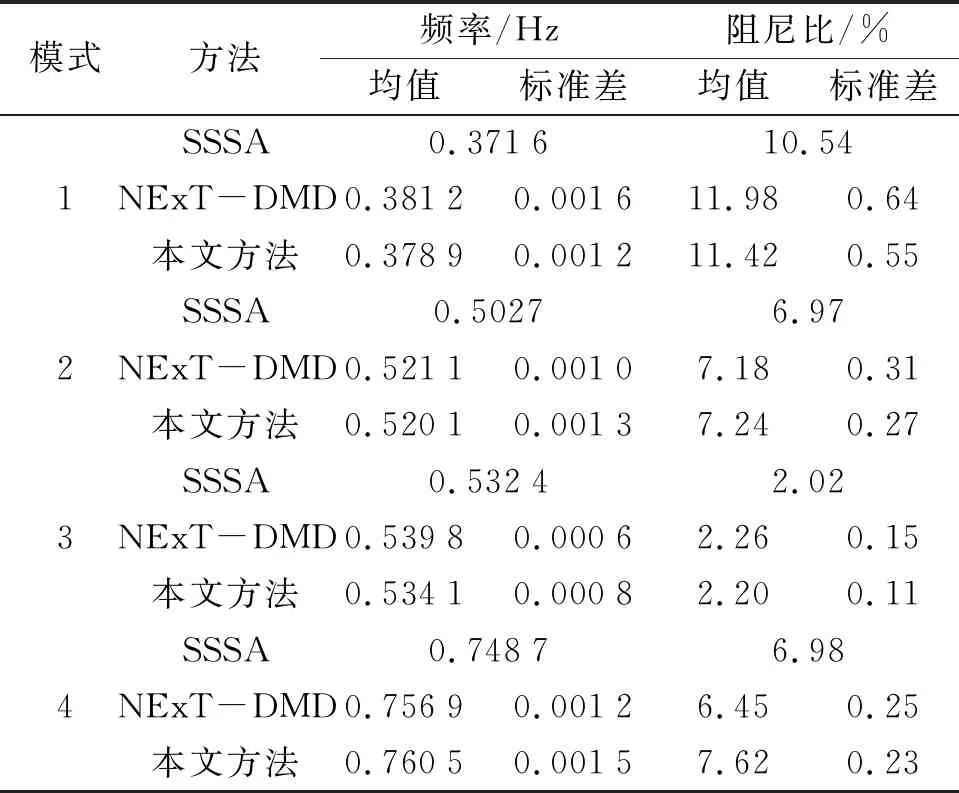
表2 16机系统不同方法机电振荡参数辨识结果对比分析

同时,为了进一步分析了本文所提辨识方法在不同负荷波动幅值下的鲁棒性和适应性,分别选取区域间模式1(阻尼比最大)和模式3(阻尼比最小)为代表,在基础运行方式(波动幅值为3%)的基础上,分别增加和减少负荷波动幅值,即分别向系统加入波动幅值为3%和5%的负荷随机波动,本文方法辨识得到的机电参数辨识结果如表3所示。

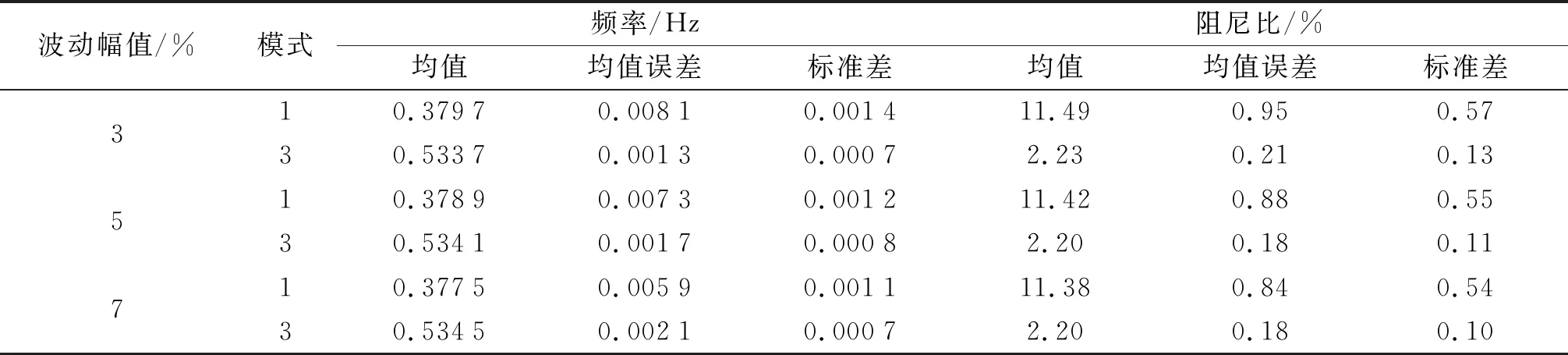
表3 不同负荷波动下机电特征参数提取结果Tab.3 Results of electromechanical feature parameter extraction under different load fluctuations

从表3对比分析结果可以看出,在不同负荷波动水平下,本文方法辨识的频率和阻尼比统计均值和标准差均变化不大,且各负荷波动水平下频率和阻尼比均值误差均较小,分别小于0.01 Hz和1%,表明本文方法对于不同负荷波动具有较好的鲁棒性,不同幅值负荷波动下均能够保证较为准确的估计结果。

图3 16机系统振荡模态图Fig.3 16 machine system oscillation mode diagram

此外,本文方法为一种基于多通道量测信号辨识方法,能够有效提取各机电模式下发电机组的相对振荡模态信息。图3给出了16机系统中十六台发电机在四个区域间模式中的相互振荡的情况。从图3可以看出,模式1为区域A和区域B的发电机与区域C、D、E三个区域的发电机的振荡;同理,模式2为区域C和区域D与区域E之间的发电机振荡;模式3为区域A与区域B发电机相互振荡;模式4为区域C和区域E与区域D发电机组之间的振荡。振荡模态辨识结果与表1中小干扰稳定分析结果一致,表明本文方法在模态振型辨识方面的有效性。

同时,利用本文方法辨识得到的各发电机组在四个区域间模式中参与因子结果,如图4所示。从图4给出的对比分析可以看出,尽管本文方法辨识得到的参与因子结果与小干扰稳定计算结果有略微差异,但在四种区域间振荡模式中表现出较高参与程度的发电机一致,验证了本文方法在参与因子提取方面的有效性。

图4 16机系统参与因子辨识结果Fig.4 16 machine system participation factor identification results

3.2 实测数据分析

通过对南方电网的随机响应数据进行分析,得到图5所示的曲线。图5(a)为南方电网的原始数据,图5(b)为该数据对应的功率谱密度,可以看到系统中含有频率为0。32 Hz和0.96 Hz两个机电模式,针对这两个模式利用本文所提方法进行机电振荡参数提取分析。

通过采用本文所提O3KID-DMD方法对连续10 min的PMU量测数据进行分析,辨识得到系统的机电模式参数(振荡频率和阻尼比),如图6所示。

由表4数据可见,使用O3KID-DMD方法提取的数据结果相较于NExT-DMD方法提取的结果更接近实测功率谱密度。并且,该方法得到的阻尼比和频率的标准差都小于NExT-DMD方法提取的标准差。因此这充分验证了本文所提方法对实际环境测量数据的适应性。

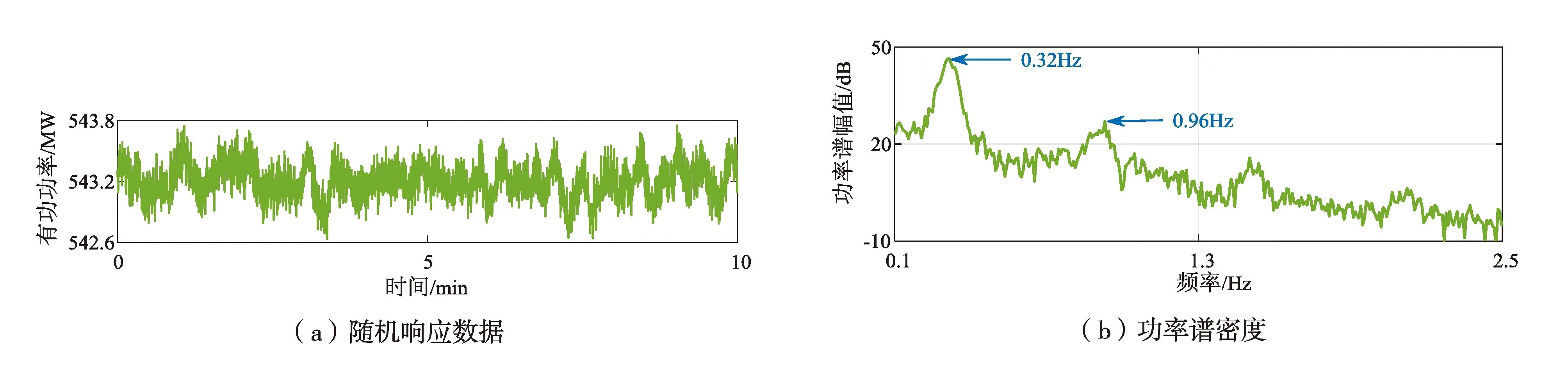
表5 南方电网的随机响应数据及对应的功率谱密度Fig.5 Random response data and corresponding power spectral density of the southern grid

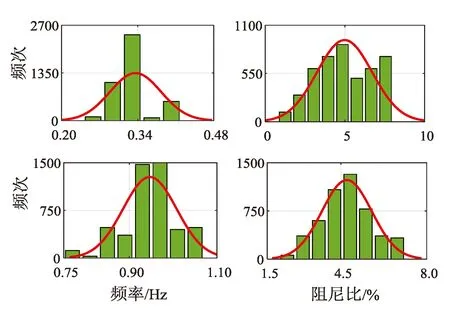
图6 用O3KID-DMD提取的两种模式机电模式参数Fig.6 Two patterns of electromechanical pattern parameters extracted with O3KID-DMD

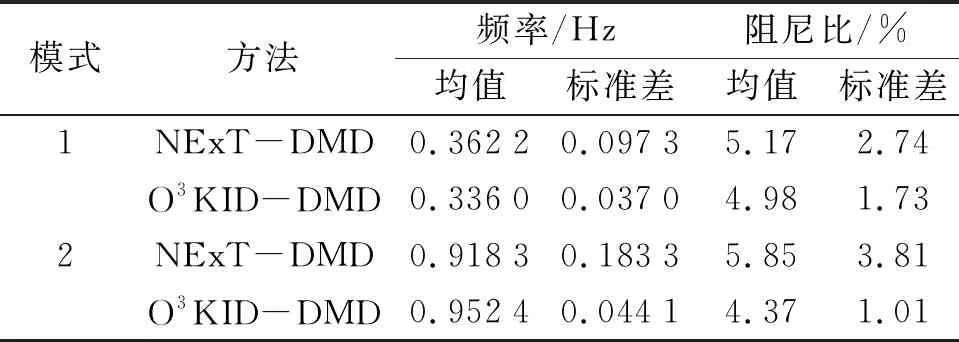
表4 O3KID-DMD和NExT-DMD方法之间的提取结果比较

4 结 论

本文提出O3KID-DMD方法,利用系统正常运行情况下随机响应量测数据辨识系统机电振荡特征参数,包括振荡频率、阻尼比、模态振型及参与因子。IEEE 16机仿真系统计算结果表明,本文所提方法能够有效从广域量测随机响应量测信号中辨识系统机电振荡参数,与NExT-DMD方法对比分析表明,两种方法均能够准确辨识系统振荡频率和阻尼比,且本文方法能够辨识得到系统各发电机组在对应模式中的参与因子,对后续机电振荡阻尼调控提供指导。研究并行计算分析以提升O3KID-DMD在线应用能力将是后序研究的重点工作。