碟形弹簧载荷与应力特性的有限元分析

李 亮，王永国，翁晓明

碟形弹簧载荷与应力特性的有限元分析

李 亮，王永国，翁晓明

（南京邦奇自动变速箱有限公司 研发中心，江苏 南京 210038）

利用ANSYS Workbench和弹塑性材料模型对碟形弹簧的载荷-位移特性和应力-位移特性进行了有限元分析，并与A-L法的理论解进行了对比。在此基础上，研究了不同的齿槽圆角和齿槽宽度对载荷-位移和应力-位移特性的影响。分析结果表明，在塑性变形阶段，有限元分析结果与A-L法的理论值差异较大。相对于A-L法，有限元法与实测值更加吻合。增大齿槽圆角会使载荷增加，增大齿槽宽度会使载荷减小。不同的齿槽圆角和齿槽宽度都会对碟簧截面四个角点的主应力有一定的影响，这为碟形弹簧的设计提供了理论依据。

碟形弹簧；有限元分析；载荷-位移特性；应力-位移特性

碟形弹簧由于占用空间小、形状可调性强、成本低等特点，应用于汽车自动变速箱或混动变速箱的湿式离合器中，为湿式离合器活塞提供准确的预紧载荷和复位载荷。为了保证湿式离合器的接合平顺性和耐久性，在设计初期阶段就首先需要对碟形弹簧进行载荷-位移特性和应力-位移特性的精确计算。

对碟簧的设计和计算常采用近似计算法和数值计算法[1]。近似计算法由于假设较多，计算结果和实验值存在一定的误差[2]。碟形弹簧载荷和应力的近似理论计算普遍采用A-L法。A-L法假设碟形弹簧的材料具有完全弹性，没有考虑材料塑性对其载荷和应力的影响，也没有考虑齿槽几何参数（齿槽宽度、齿槽圆角）的影响。

利用有限元法来求解碟形弹簧是一种十分有效的数值计算方法。基于数值模拟的普通碟簧的力学性能研究已有一定的基础[1]，但是公开发表的研究碟形弹簧弹塑性力学特性和齿槽几何参数影响的有限元分析论文很少。

本文基于ANSYS Workbench和弹塑性材料模型，对碟形弹簧进行了有限元计算，得出了载荷-位移和应力-位移特性曲线，并与A-L法的理论解进行了对比。在此基础上，进一步研究了齿槽几何参数（齿槽宽度、齿槽圆角）对其载荷-位移特性和应力-位移特性的影响，为碟形弹簧的有限元计算和设计提供了指导和参考。

1 碟形弹簧的A-L法

A-L法于1936年提出，采用假设进行简化分析，利用板壳理论推导代数方程，得出理论解。

在A-L法采用以下列假设[3]：

1）碟形弹簧的矩形截面绕其中性点转动，转角与变形量之间的关系是线性的，矩形截面本身也没有变形；

2）碟形弹簧的载荷和支反力均匀分布在内圆周和外圆周上，且不考虑与上、下支撑面之间的滑动摩擦；

3）碟形弹簧材料是线弹性体，具有完全弹性，应力-应变关系符合虎克定律，没有塑性变形；

4）受载变形时，碟形弹簧与上、下支撑面的接触点保持不变。

图1为碟形弹簧截面示意图。式（1）为碟形弹簧的载荷-变形公式（A-L式）[4]。A-L式形式简单，便于计算。

图1 碟形弹簧的矩形截面

式中，为轴向载荷；为外径；为内径；为厚度；为变形量；为泊松比；0为内截锥高度。

2 几何参数

图2为一个碟形弹簧尺寸示意图，由碟簧部分A和舌片部分B组成。材料为65 Mn，厚度为0.7 mm，内径圆周表面上的舌片之间开有24个均布的径向槽，齿槽圆角为R1，齿槽宽度为5.7 mm。

图2 碟形弹簧的几何参数

3 有限元分析

3.1 网格划分

离散后的装配体模型如图3所示。为了保证计算精度并减小计算规模，采用1/24圆周循环对称的三维模型。碟形弹簧两侧的旋转对称面网格单元为匹配控制。单元尺寸为0.15 mm，类型为Hex20，节点数为155 492。为了准确地得到碟形弹簧自身的载荷-位移特性，定义上、下支撑面的实体均为刚体。

图3 网格划分结果

3.2 应力-应变关系

碟形弹簧在工作时，其局部材料会进入塑性区，要准确地计算碟簧在工作过程中的应力，需要对其展开弹塑性分析[5]。弹性阶段为线性的应力-应变关系，弹性模量为212 000 MPa，泊松比为0.3，屈服强度为1 500 MPa。塑性阶段的应力-应变关系采用双线性随动强化模型，屈服后的强化模量为2 500 MPa。

3.3 边界条件

对上支撑面施加方向的位移，约束其他方向的自由度。约束下支撑面所有方向的自由度。

为了与A-L法的假设保持一致，定义碟形弹簧的上、下支撑面均为无摩擦接触。接触方程为增广拉格朗日乘子法。为保证收敛性，经初步试算后，确定上、下支撑面的法向刚度系数均取为0.1。

3.4 载荷-位移特性

求解后提取支反力，图4显示了载荷与位移之间的关系。

图4 载荷-位移特性曲线

相对于A-L法，有限元法与实测值更加吻合，误差最大为3.3%。有限元法载荷计算值和实测值要比A-L法要小，差值随着位移量的增大而逐渐增大。比如：在位移为2 mm时，A-L法与实测值之间的差值为59 N，而在位移为0.8 mm，差值达到了104 N。两者差异增大的主要原因是A-L法假设材料是线弹性体，没有考虑塑性变形的影响。

3.5 应力-位移特性

如图5所示，选取位于碟簧区域的循环对称截面上的4个角点，并定义为I、II、III、IV。点I和点II分别对应碟簧区域内径的上、下缘，点III和点IV对应碟簧区域外径的下、上缘。

图5 碟簧区域的4个角点

求解后提取的各个角点主应力如图6所示，实线为各点的有限元法计算结果，虚线为对应各点的A-L法计算结果。正的应力值代表拉应力，负的应力值代表压应力。由图6可以看出：I点受压，而III点受拉，有限元法得出的主应力绝对值要小于A-L法。对于有限元法，这两处角点在进入塑性区域后，位移量持续增加，但应力值几乎保持不变，与A-L法的应力差值越来越大。II点先受压再受拉，而IV点先受拉再受压，这两处角点随着位移量的增加，有限元法和A-L法的应力差值趋于稳定。

图6 应力-位移特性曲线

4 齿槽参数的影响

齿槽参数包括齿槽圆角和齿槽宽度。通过有限元法研究齿槽参数对其载荷和应力的影响。

4.1 齿槽圆角的影响

图7显示了齿槽圆角分别为R0.5、R1、R1.5（其他参数相同）时的载荷-位移特性曲线。

图7 不同齿槽圆角的载荷-位移特性曲线

由图7可以得出：齿槽圆角越大，载荷越大。这是因为增大齿槽圆角可以增加结构刚度，在相同的位移下，载荷会随之增大。

图8显示了齿槽圆角分别为R0.5、R1、R1.5（其他参数相同）时的应力-位移特性曲线。

图8 不同齿槽圆角的应力-位移特性曲线

由图8可以得出：增大齿槽圆角会使角点I的压应力绝对值和角点III的拉应力增加，但这两处角点在进入塑性区域后，主应力值趋于相同。对于角点II，增大齿槽圆角会使其压应力绝对值增加，拉应力减小。对于角点IV，则与之相反。对于角点II和IV，随着位移量增加，不同齿槽圆角相互之间的应力差值趋于稳定。

4.2 齿槽宽度的影响

图9显示了齿槽宽度分别为4.7 mm、5.7 mm、6.7 mm（其他参数相同）时的载荷-位移特性曲线。

由图9可以得出：齿槽宽度越大，载荷越小。这是因为增大齿槽宽度会减小结构刚度，在相同的位移下，载荷会随之变小。

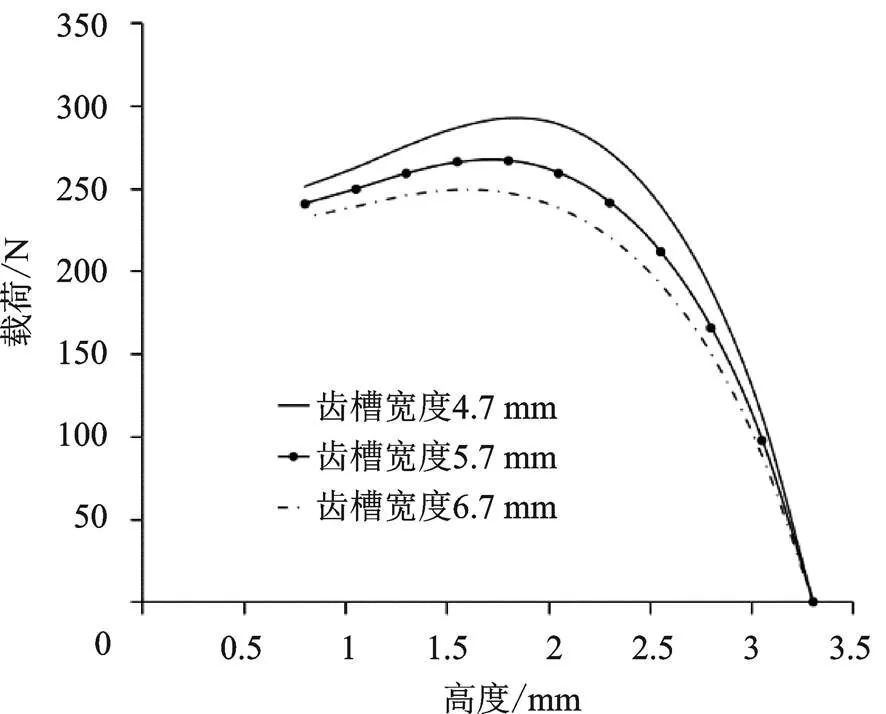
图9 不同齿槽宽度的载荷-位移特性曲线

图10显示了齿槽宽度分别为4.7 mm、5.7 mm、6.7 mm（其他参数相同）时的应力-位移特性曲线。

图10 不同齿槽宽度的应力-位移特性曲线

由图10可以得出：增大齿槽宽度会使角点I的压应力绝对值和角点III的拉应力减小，但这两处角点在进入塑性区域后，主应力值趋于相同。对于角点II，增大齿槽宽度会使其压应力绝对值减小，拉应力增加。对于角点IV，则与之相反。对于角点II和IV，随着位移量增加，不同齿槽宽度相互之间的应力差值趋于稳定。

5 结论

通过碟形弹簧的有限元分析对比了有限元计算与A-L法的差异，分析了不同齿槽圆角和齿槽宽度对载荷和应力-位移特性的影响。得出以下结论：

1）相对于A-L法，有限元分析得出的载荷值与实际更吻合；

2）在塑性变形阶段，有限元法得出的载荷值和应力值与A-L法的理论值差异较大；

3）增大齿槽圆角会使载荷增加。不同的齿槽圆角会对碟簧截面4个角点的主应力有一定的影响；

4）增大齿槽宽度会使载荷减小。不同的齿槽宽度会对碟簧截面4个角点的主应力有一定的影响。

[1] 张少军,赵思岩,朱冬梅,等.碟簧力学性能试验及仿真分析[J].湖南大学学报:自然科学版,2018,45(4): 64-73.

[2] 王英浩,李文斌,王川云,等.基于有限元的航天器用碟形弹簧优化设计[J].导弹与航天运载技术,2013 (6):51-55.

[3] 林世裕.膜片弹簧与碟形弹簧离合器的设计与制造[M].南京:东南大学出版社,1995:25.

[4] 全国弹簧标准化技术委员会.碟形弹簧:GB/T 1972—2005[S].北京:中国国家标准化管理委员会,2005.

[5] 廖日东,左正兴.飞行器结构分离碟形弹簧大位移弹塑性有限元分析[J].兵工学报,2006,27(4):702-707.

Finite Element Analysis on Load and Stress Characteristics of Disc Spring

LI Liang, WANG Yongguo, WENG Xiaoming

( Department of Research and Development,Nanjing Punch Powertrain Company Limited, Nanjing 210038, China )

The load-displacement and stress-displacement characteristics of disc spring are analysed by using ANSYS Workbench and elastoplastic material models,and compared with the theoretical results of the A-L method. On this basis, the effects of different slot fillets and slot widths on load-displacement and stress-displacement characteristics are studied.The analysis results show that in the plastic deformation stage, the finite element analysis results are quite different from the theoretical values of the A-L method. Compared with the A-L method, the finite element method is more consistent with the measured values. Increasing the slot fillet increases the load, and increasing the slot width decreases the load. Different slot fillets and slot widths will have a certain influence on the principal stresses at the four corner points of the disc spring section. This provides a theoretical basis for the design of disc springs.

Disc spring;Finite element analysis;Load-displacement characteristic;Stress-displace- ment characteristic

U462

A

1671-7988(2023)10-144-05

10.16638/j.cnki.1671-7988.2023.010.030

李亮（1984—），男，硕士，工程师，研究方向为自动变速箱开发，E-mail:victor.li@punchpowertrain.com。