基于多视角红外传感器的三维重建方法

2023-06-13宋丽梅张继鹏李云鹏刘镇宁

液晶与显示 2023年6期

宋丽梅，张继鹏，李云鹏，刘镇宁，罗菁

（天津工业大学天津市电气装备智能控制重点实验室，天津 300387）

1 引言

计算机运算能力的快速提高极大地促进了机器视觉技术在各个领域的发展，三维重建技术作为其中的一项重要组成部分已经被广泛应用于逆向工程设计、工业检测与识别和人体测量等多个领域。多视图点云拼接作为三维重建技术中的研究重点，其难度远高于两两点云视图拼接，是三维重建领域研究的热点问题［1］。

非接触式三维重建技术的成像通常受到传感器视场范围的约束，所以必须将多个不同视角下的点云进行拼接才能对被测物体进行全貌成像。目前使用最多的三维点云配准方法是由Besl等人提出的ICP 算法［2］。该算法虽然有较好的鲁棒性和稳定性，但是容易陷入局部最优解，导致错误的匹配结果，并且对于特征点较少的物体，点云配准精度较低。为提高ICP 算法求解全局优化问题的工作质量，Artyom［3］等人提出了正则点云配准方法。Zhao［4］等人提出改进的3DSC-ICP 点云配准方法，在提升配准效率的同时也解决了ICP 配准算法陷入局部最优的缺点。

随着深度学习［5-6］的发展，神经网络也被应用于点云配准工作当中。Li［7］等人提出了名为VPRNet 的新型网络，用于部分到部分点云配准的深度学习网络，但网络对于大型点云的配准精度不高。Xin［8］等人提出了一种基于BP 神经网络和位移窗技术的鲁棒粗到细配准方法，降低了配准时间和空间复杂度。Chang［9］等人开发了一种估计物体相对姿态的配准结构，经过训练后，所提出的架构可以估计模型点云与数据点云之间的旋转，然后根据计算平均值进行平移估计。Zuo［10］等人提出了一种基于单次深度学习的双频复合条纹投影轮廓测量方法，可以实现更高质量的相位信息提取和更鲁棒的复杂表面物体的相位展开。Nicolas［11］等人提出了一种基于深度学习的快速迭代切片传输的点云配准方法，通过多次迭代实现点云的配准。Li［12］等人提出了一种基于深度学习的离群值去除点云配准方法，经过训练后能够快速、准确地去除离散点，实现点云配准。

基于世界坐标系转换的三维点云拼接方法也被广泛应用。Meng［13］等人提出了一种基于电磁追踪系统的点云配准方法，利用电磁追踪系统高准确度的位移和姿态角信息，通过不同坐标系间的快速转换，实现点云的快速配准。Qiu［14］等人提出了一种快速的多向仿射配准算法（FMDAR），可以有效地转换复杂的数据。然而，FMDAR 算法不能配准严重不完整和严重变形的点云。Diao［15］等人提出了一种基于参考对象空间关系的点云拼接方法，可以对参考特征不足的点云进行拼接并保证了一定的拼接速度。Zuo［16］等人提出了一种结合结构光和光场特性进行无相位展开三维重建的方法，有效地避免了一次测量所产生的随机误差。

本文设计了一种基于双目相机多视角传感器三维点云的成像系统，将线激光器与双目相机组合成为一个扫描支柱。在扫描过程中，激光器将红外激光投射到目标物体上，双目相机通过采集物体上反射的线激光计算出物体的深度信息进而生成点云。在扫描系统中，本文提出了一种基于多视角传感器轴线融合的点云拼接方法，该方法可以快速、准确地将多视角下的三维点云进行拼接。

2 三维重建系统构成及其工作原理

考虑到相机的景深、测量角度以及红外激光器的投射范围，本文设计的三维重建系统如图1所示。系统由4个扫描支柱组成，每个扫描支柱在空间位置上构成一个边长为2.5 m 的正方形。系统的工作范围为1.3～1.9 m。每个扫描支柱包括两个型号为MV-CU013-A0UC 的工业相机、型号为M0814-MP 的8 mm 镜头、型号为HO-Y635P5-1030 的780 nm 红外激光发射器、型号为E6B2-CWZ6C 的编码器、CAN 总线步进电机及其驱动器。

图1 三维重建系统及其组成部分Fig.1 3D reconstruction system and its components

当三维重建系统工作时，首先由激光发射器向被测物体上投射不可见红外激光，然后由相机同步采集所投射激光条纹位置的纹理图像用以生成点云，最后步进电机控制的移动滑台带动激光发射器和步进电机向上运动，完成被测物体表面的三维重建。为了控制点云数据的间隔距离，本文设计的基于双目相机多视角点云的三维成像系统利用产生外触发信号的编码器控制摄像机采集所需条纹图像和纹理图像。

2.1 相机参数的获取

要还原摄像机所拍摄的物体在真实空间的位置就要知道世界中的物体到计算机图像平面的转换关系。要建立相机与世界坐标系之间的关系，需要对相机进行标定，求解出相机的内外参数。相机的透视投影会使采集到的图片产生畸变从而影响重建的精度，相机标定的另一个目的就是计算出畸变系数用于图像矫正。

双目立体视觉类似人体的双眼，它采用两台相同的工业相机从不同的角度拍摄待测物体，找到两幅图像中公共区域的匹配点，计算出该点的三维坐标。双目立体视觉系统成像的前提是进行双目标定，计算出两个相机之间的旋转矩阵R和平移矩阵T。本文利用张正友标定方法对双目相机进行标定，从而分别得到左右相机与世界坐标系之间的转换关系RL、TL和RR、TR以及左右相机的畸变参数和内参。

2.2 轴线标定原理

本文所提出的基于多视角传感器轴线融合的点云拼接方法流程如图2 所示。标定利用高精度位移旋转台带动平面靶标进行同轴转动，通过传感器多次的数据采集得到一系列绕转台轴线旋转的点集。通过对点集的处理，计算出精确的轴线向量以及轴线上的任一点在世界坐标系下的具体位置。

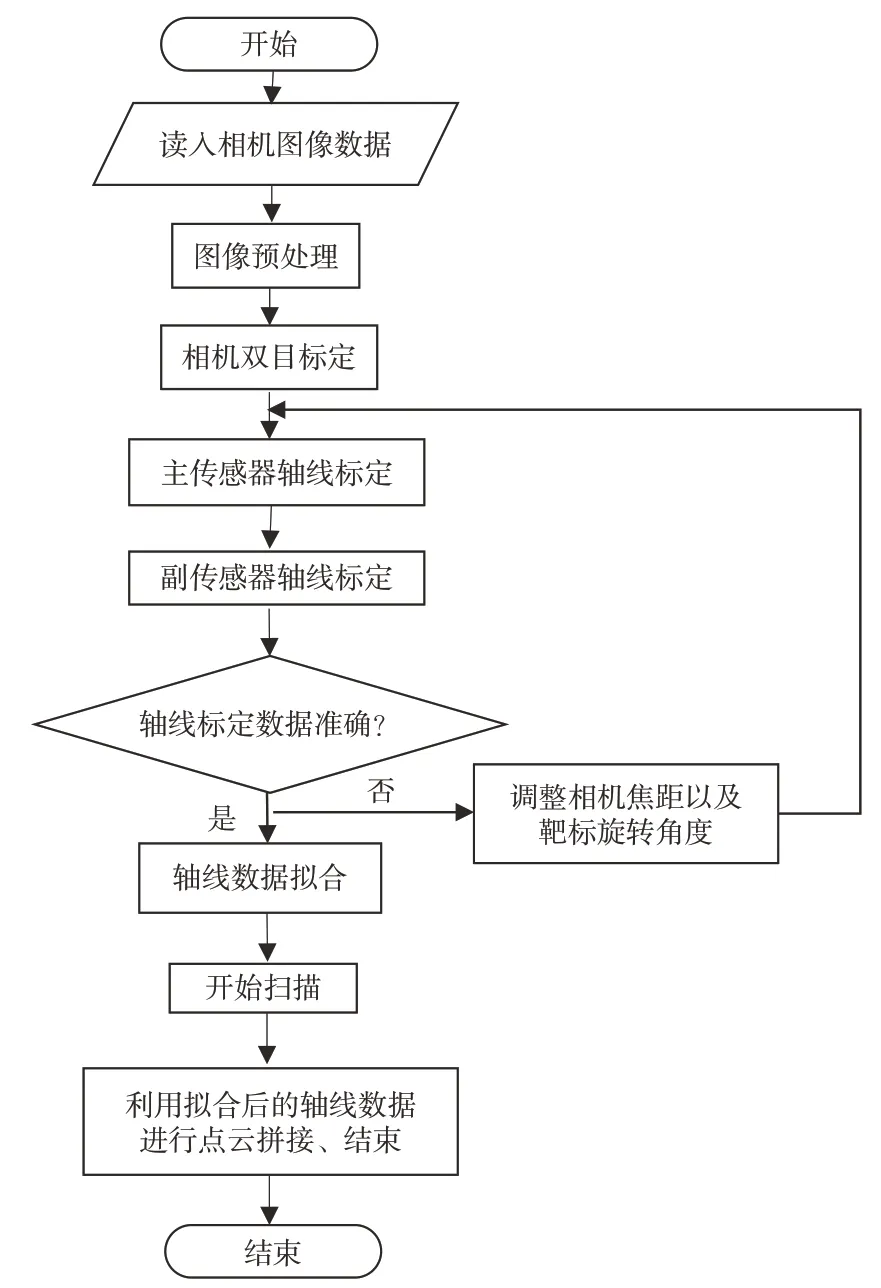
图2 本文所提出的点云拼接方法流程图Fig.2 Flowchart of point cloud splicing method proposed in this paper

数据点在采集时会存在一定的精度误差，造成多视角传感器扫描出来的点云拼接存在拼接错位、点云远离轴线等问题。本文提出的多传感器多轴线融合的点云拼接方法利用在不同位置下的多组双目传感器采集平面靶标在同一位置下的旋转点集，分别计算出双目传感器所对应的轴线向量，对多组轴线向量进行拟合，求解出误差最小的轴线向量。利用求解出来的轴线向量进行点云拼接具有精度高、速度快、稳定性高的优势。

如图3 所示建立坐标系，其中ocl-xclyclzcl为左相机坐标系，ocr-xcrycrzcr为右相机坐标系，Ow-XwYwZw为世界坐标系，OL-ULVL为左相机图像坐标系，OR-URVR为右相机图像坐标系。

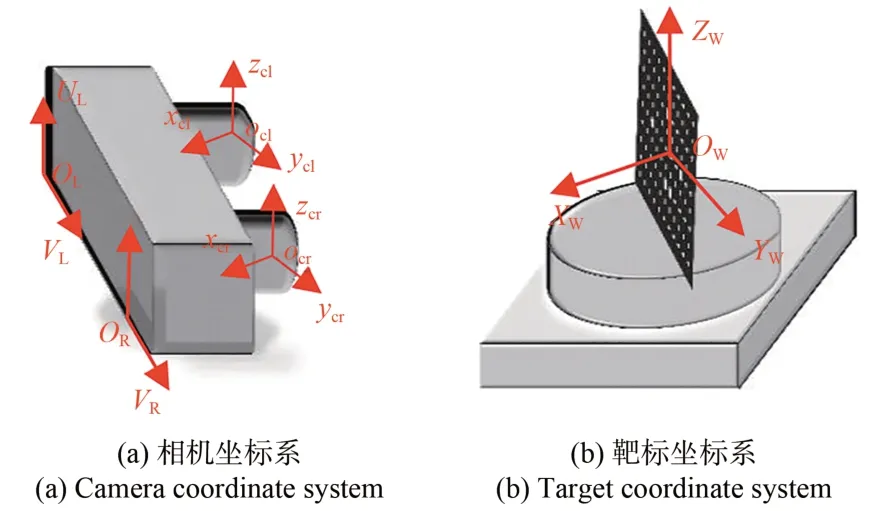
图3 相机与靶标坐标系Fig.3 Camera and target coordinate system

设世界坐标系下有一点Ow，该点在左右相机坐标系下对应的点分别为ocl和ocr，在左右相机的成像平面坐标系下映射的像素坐标分别为(ul，vl)，(ur，vr)，则有如式（1）所示关系：其中：Al和Ar为相机的内参矩阵，Rl、Rr、Tl、Tr为相机的外参矩阵，内参矩阵和外参矩阵均由双目标定结果可知。由公式（1）可知，若获得左右相机平面中对应的像素坐标(u，v)，即可求得该像素点在世界坐标系下对应的三维坐标。

将公式（1）进一步变换可消去zcl和zcr两个未知数，得到一个超定方程组：

进一步写为公式（2）：

为了获得空间点绕轴线旋转前后的关系，需要计算出转台轴线方程在世界坐标系的参数和已知的旋转角度。本文提出的多传感器多轴线融合的点云拼接方法其思路如下：

通过双目标定建立世界坐标系，利用高精度旋转台带动靶标进行绕轴线旋转的运动，采集不同角度下的靶标图像。先利用轴线标定的结果得到每个标定板上圆的圆心绕旋转轴旋转的点集P1，再利用该点集计算得到一系列轨迹圆的圆心，最后拟合所求圆心计算出旋转轴的轴线在世界坐标系中的位置。为了提高点云拼接精度，提升系统的稳定性，本文利用多组传感器从不同角度进行轴线数据采集，最终解算出最优轴线向量，具体的实现步骤如下：

（1）利用轴线标定的结果分别得到4组传感器下的靶标绕旋转轴运动的点集。

（2）求解出点集中每个点绕旋转轴运动形成的空间圆轨迹的圆心，设其中一组传感器所有求出的圆心的集合为Oi，则这些圆心位于旋转轴的不同位置上。

（3）其中一组传感器拟合出经过圆心点集Oi的三维空间直线L，L即为该组传感器所计算出的空间轴线。

（4）其他3 组传感器分别利用上述方法解算出各自对应的空间轴线。

（5）将4 组传感器分别解算出的空间轴线进行拟合，计算得到最优空间轴线。

在转台旋转过程中，理论上同一个点的轨迹圆上的所有测量点都应该处于同一平面，但是实际测量过程中存在误差，会造成解算出的轴线偏离实际的旋转轴而导致生成的点云拼接不准。本文所提出的多传感器多轴线融合的点云拼接方法正是消除了这种误差，提高了点云的拼接精度。

由于空间圆可以描述为一个空间平面和一个空间球相交，因此可以分为3 步来拟合，具体步骤如下：

（1）拟合轨迹点所在的球面方程

空间圆球的方程如式（3）所示：

（2）拟合轨迹点所在的平面方程

空间平面方程可以描述为公式（7）：

将所测得到的空间圆心带入式（7）中得到公式（8）：

矩阵变换得到公式（9）：

根据最小二乘法可以求得A'、B'、C'的参数，联立空间平面方程与球面方程可以求得空间圆的半径R和圆心坐标(Oa，Ob，Oc)。

（3）利用RANStAC 算法将4 组传感器采集并计算出的数据进行解算分别得到各自的轴线向量。

3 实验与结果

3.1 多视角传感器轴线标定

扫描系统进行轴线标定之前需要进行双目标定。本文进行双目标定时采用的靶标为10×10 圆点阵列靶标，圆心间距为20 mm，加工精度为1 μm，使用张正友标定方法。在实验过程中，靶标与相机之间的距离为1.7 m。为保证双目标定精度，采集12幅不同位置的靶标图像作为标定图像。

双目标定后，利用高精度移动转台带动靶标绕转台旋转轴运动，采集不同角度下的靶标图像进行主传感器的轴线标定。由于靶标平面的特征明显，利用数据图像处理的方法识别出靶标上的圆，将在靶标上提取到的100个圆按顺序排列，得到100 个相互匹配的点对。假设其中一个的点对在左右相机像素坐标系下的坐标分别为pl(uil，vil)和pr(uir，vir)，将pl和pr带入公式（2）即可求得对应点的三维坐标(xi，yi，zi)。

点位提取是轴线标定精度的关键。本实验中主传感器和副传感器点位提取结果和轴线数据标定结果如图4 所示。单幅图像在空间中的排列关系符合实际物理关系。由于双目相机的视场范围有限，为防止平面靶标在偏离一定角度之后出现圆心提取误差较大甚至无法提取的情况，本文将高精度位移旋转台的移动角度固定为-26°～26°，每次旋转1°，得到一系列绕轴旋转的点集，再利用这些点进行圆的拟合求取轴线数据。

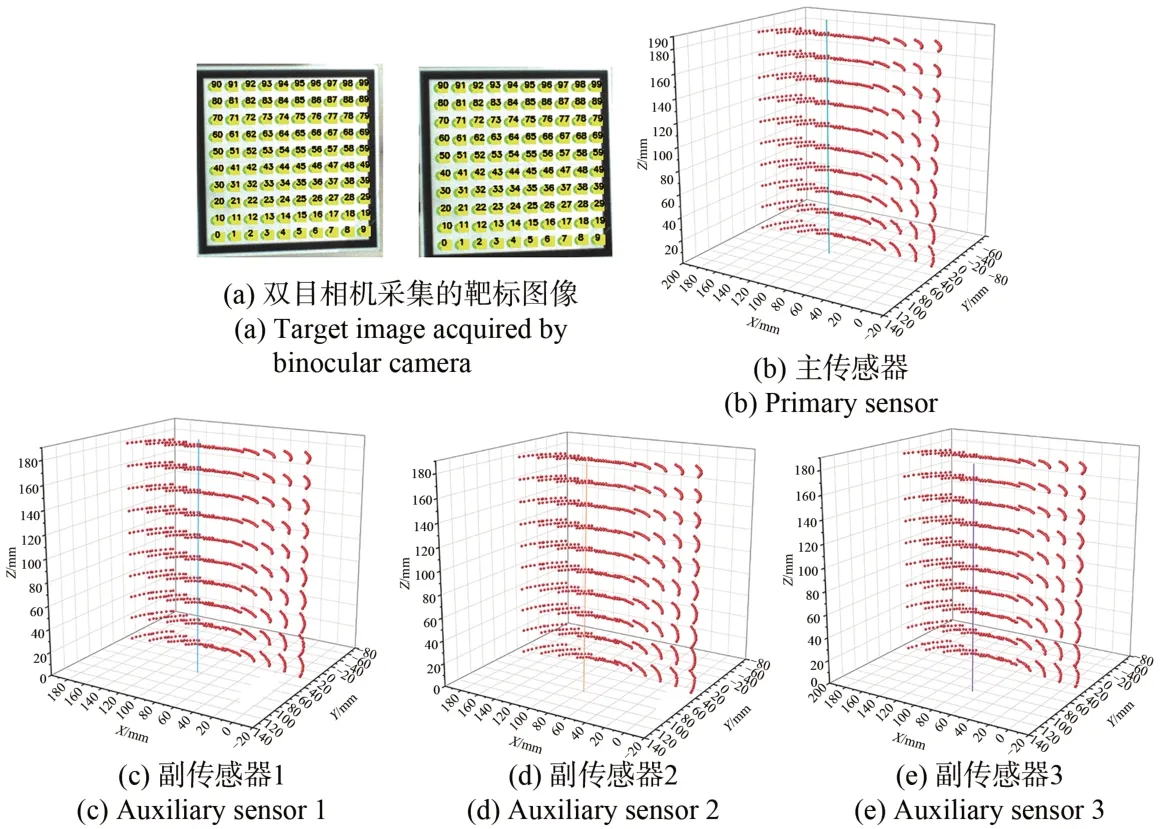
图4 主传感器和副传感器点位提取结果与轴线标定结果Fig.4 Point extraction results of main sensor and secondary sensor and axis calibration results

经过实验分析发现，利用此方法虽然能够较为精准地解算出轴线向量以及在轴线上任意一点的世界坐标，但稳定性较差。在三维重建过程中计算出的相对点云位置关系误差较大，影响点云拼接的精度。在此基础上，本文引入了其他3 组扫描系统作为辅助标定系统，从而计算出高精度的轴线向量。

3.2 多传感器轴线拟合

完成主、副传感器的双目标定以及轴线标定，分别获取主传感器和3 个副传感器的世界坐标系下的转台轴线方程。理论上，由于4 个传感器的世界坐标系均以靶标上同一点作为原点，因此转台轴线的信息在4 个传感器的世界坐标系下均一致。但在实际的标定过程中，受系统的随机装配误差和轴线拟合算法误差影响，得到的轴线信息无法保持一致。因此本文提出一种基于最小二乘的多轴线二次融合方法，利用等距平面分别截取4 个传感器得到的转台轴线方程，将截得的空间点进行二次轴线拟合，以此来减小由于多传感器装配误差引起的轴线拟合的误差。

利用第2.2 节所述的轴线标定方法，将各个传感器获取的转台轴线方程记为公式（10）：

当i=0 时，该方程为主传感器获取的轴线方程，将此轴线记为N0；当i=1 时，该方程为副传感器1 获取的轴线方程，将此轴线记为N1；当i=2 时，该方程为副传感器2 获取的轴线方程，将此轴线记为N2；当i=3 时，该方程为副传感器3 获取的轴线方程，将此轴线记为N3。

根据几何关系，不相互平行的空间平面与空间直线交于一点。如图5 所示，结合坐标系与旋转轴的关系，可知理论上转台的旋转轴的方向向量与世界坐标系的z轴平行，取平面Z=zj对轴线N0、N1、N2、N3进行截取，得到4个分别位于轴线上的点jh0、jh1、jh2和jh3，则jhi可如式（11）表示：

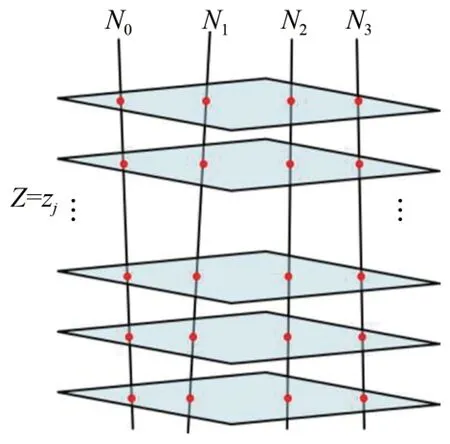
图5 多轴线二次融合采样过程Fig.5 Multi-axis secondary fusion sampling process

根据本文不同的双目视觉传感器获取的不同的转台轴线，可知每一个平面Z=zj可截得4 个空间点。由于空间轴线与空间平面截得的空间点均由真实的轴线截得，因此对不同平面截得的空间点进行融合，通过式（12）进行融合后的空间点三维坐标求解：

其中：(um，vm，wm)为经过多轴融合的轴线的方向向量，(xm，ym，zm)为该轴线上一点。利用式（13），即可完成多传感器条件下的多视角点云拼接。

根据本节中的方法，对4 组传感器得到的转台轴线进行采样，采样得到的轴线数据如图6 所示。对多个传感器得到的空间轴线进行融合，得到的轴线最终结果如图7 所示。其中各个传感器得到的轴线向量和多轴线融合后的最终向量如表1 所示。

表1 各组传感器轴线标定结果Tab.1 Axis calibration results of each sensor

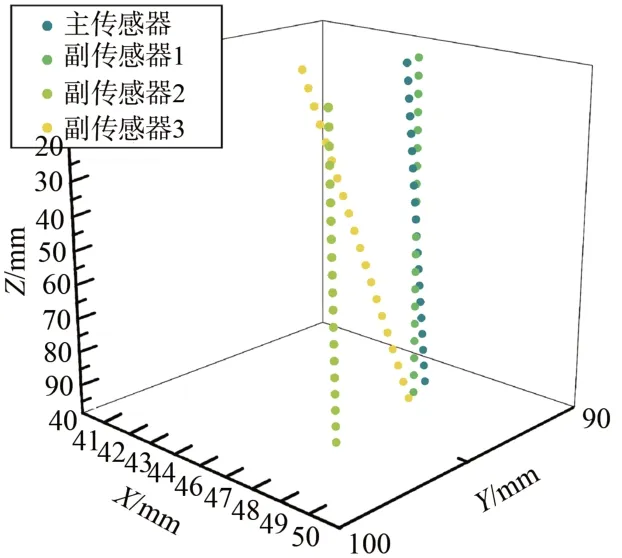
图6 多传感器轴线数据Fig.6 Multi-sensor axis data

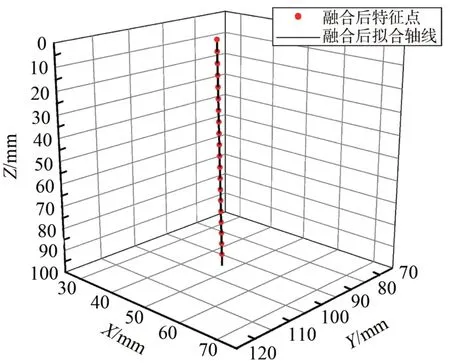
图7 多轴线融合后的特征点及轴线Fig.7 Feature points and axes after multi-axis fusion

3.3 三维重建精度分析

为了进一步证明本文提出的基于多视角传感器轴线融合的点云拼接方法的优越性，在测量范围为1.3～1.9 m之内，选取了直径为144.954 2 mm的标准球进行精度评价（图8）。

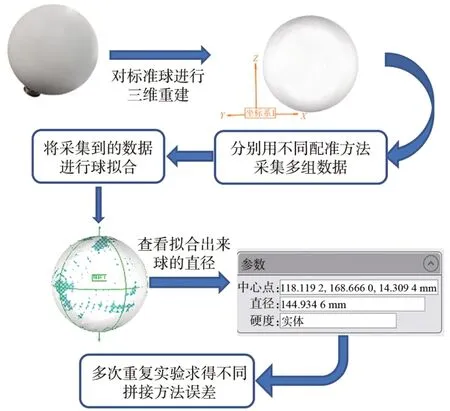
图8 精度评价实验流程图Fig.8 Flow chart of accuracy evaluation experiment

分别使用单轴线三维点云配准方法、最近点迭代算法点云配准方法、深度学习的离群值去除点云配准方法、多视角传感器轴线融合的三维点云配准方法对标准球进行三维重建，并对重建后的标准球直径进行误差分析。其中最大误差为MAXerr，平均绝对误差为MAEerr，均方根误差为RMSEerr。由表2 可知，本文所提出的点云拼接方法将误差控制在0.037 mm 以内，其他方法得到的误差均较大，证明本文所提出的多视角传感器轴线融合的三维点云配准方法优于其他点云配准方法。由表3 可知，本文方法的点云拼接时间为0.517 s,亦优于其他方法。

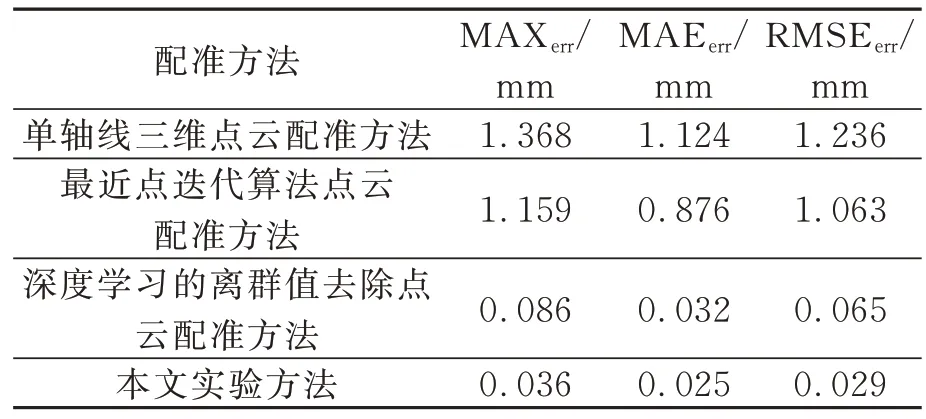
表2 标准球的误差分析Tab.2 Error analysis of standard ball

表3 标准球的点云拼接时间对比Tab.3 Comparison of point cloud splicing time of standard ball

3.4 多视角传感器点云拼接效果

本实验是在测量范围为1.3～1.9 m 内使用直径约为160 mm 的圆柱与宽约47 cm 的人体模特上进行点云拼接效果显示。在每个实验中对单轴线三维点云配准方法、最近点迭代算法点云配准方法、深度学习的离群值去除点云配准方法、多视角传感器轴线融合的三维点云配准方法4 种拼接方法进行对比。本实验首先对物体的真实纹理信息进行拼接展示，再去除三维点云的RGB信息进行拼接效果细节显示。

为了在更多类型的对象上测试我们的方法，对无特征点物体和有特征点物体进行了三维扫描，如图9 和图10 所示。显示最终的点云并分析其点云横截面与拼接缝隙。从实验中可以看出，本文方法获得的轴线信息可以很好地从各个角度拼接出三维物体的点云。

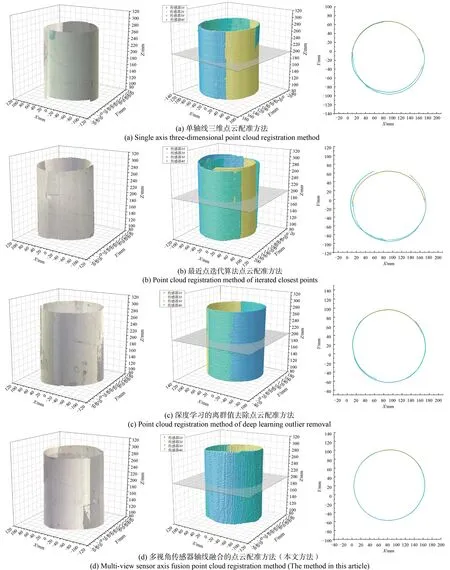
图9 标准圆柱拼接效果及截平面效果各种方法对比Fig.9 Comparison of standard cylindrical splicing effect and sectional plane effect

图10 人体模特拼接效果各种方法对比Fig.10 Comparison of mannequin splicing effect

图9 显示了无特征点物体的点云拼接效果。本文提出的配准方法拼接时间为0.817 s。理论上，同一圆柱形物体不同视角的点云应该是连续曲面，其切面也应该是连续曲线。但是，其他方法得到的拼接结果在不同切片的点云之间存在不同程度的分层。图10 显示了有特征点物体的点云拼接效果。本文提出的配准方法的拼接时间为0.916 s，与传统的最近点迭代算法点云配准方法相比，提高了点云的配准效率。对于有特征点物体的点云拼接的连接处应该是连续且光滑的曲面，但是，其他方法得到的拼接效果在点云拼接的连接处有不同程度的缝隙。从实验结果可以看出，本文提出的点云拼接方法对物体具有更好的拼接效果。