傅里叶叠层显微术的光源位姿校正

郑传建，杨德隆，张韶辉，胡 摇，郝 群

（北京理工大学 光电学院，北京 100081）

1 引 言

生命之美源于细胞结构与行为的复杂多样性。判天地之美，析万物之理，人类探索世界规律的脚步从未停止。得益于16世纪末显微镜的诞生，人类可以通过显微镜观察和理解微观世界，但想要深究生命的奥秘，显微镜就必须能够观测更加精细的微观结构，例如尺度在几纳米到几百纳米的细胞器和生物大分子。不幸的是，阿贝衍射理论［1］早已确定传统显微镜的衍射分辨率极限为200 nm，远远低于生命科学的观测需求。如今，显微成像技术不断革新，发展成为了生物医学、生命科学和工业检测等领域不可或缺的重要工具。但是，传统显微镜“所见即所得”的成像模式并没有发生根本性的变革，在面对现代科学研究所提出的实时超分辨成像［2］和高通量成像［3］等要求时，传统显微镜显得愈加无能为力，尤其在以下两个方面：

（1）难以实现大空间带宽积成像。空间带宽积是用于表征系统传输信息能力的物理量［4］，可以用成像视场内能够分辨的最多像元数来表示。为了提高显微系统的信息传输能力，就要提高成像分辨率或扩大成像视场。2014 年诺贝尔化学奖授予了光激活定位显微术（Photo Activated Localization Microscopy，PALM）和受激发射损耗显微术（STimulated Emission Depletion，STED）两项超分辨率荧光显微技术［5］，可见高分辨率显微成像对人类科学技术发展的重要推动作用。但是，因为显微镜分辨率与成像视场之间的固有矛盾，在提高分辨率的同时，成像视场将减小，使得传统显微镜的空间带宽积难以提升，停留在百兆数量级。为了同时实现大视场和高分辨率的成像，常规显微镜系统一般利用精密机械移动平台控制样本或者镜头实现空间扫描，再通过图像拼接融合算法将采集的多个小视场结合［6］，得到最终的大视场图像，但引入精密机械平台也意味着系统体积和成本的增加。

（2）对透明样本成像工序复杂。光学显微镜通过光波与样本的相互作用，将样本的信息调制到光波的复振幅上，再通过人眼观察或图像传感器记录光波以获得样本的信息。然而，人眼和传感器的响应速度都难以企及光波1014Hz 的相位信息，只能获得光波的振幅信息，这一缺陷使常规显微镜在观测透明的生物细胞或组织时需要增加额外的工序，以提高成像对比度。该工序一般可以分为两类，第一类是通过外源性的标记物，如荧光造影剂标记样本。由于样本不同部分对于特定染料的亲和度的差异性，激发的荧光光谱可以明显区分，从而提高成像对比度。但荧光剂的光毒性和光漂白性可能会影响细胞的结构与行为，难以实现对细胞的动态观测。第二类工序是间接地对光波的相位成像，它的无标记特性使长时间的动态观测成为了可能，分为定性和定量相位成像。经典的定性相位成像的方法是Zernike相衬［7］，在频谱面通过相位板对零频分量添加π/2 的相位延迟，可以实现高对比度的成像，但因为该方法对相位的响应是非线性的，只能定性反映样本相位变化，难以得到细胞的表面特征和内部结构。定量的相位成像技术可以分为光强传输方程测量［8-9］、干涉相位测量［10］和衍射相位测量［11］。光强传输方程测量的基本原理是光波的相位会改变光波在平行于光轴方向平面内的强度分布，通过建立强度变化量与相位之间的关系式，可以间接测量强度变化来求解相位信息。但该技术在采集不同面的强度信息时仍然需要依赖机械平移台移动像面或物面，高精度、高稳定性的移动台会急剧增大系统成本。干涉相位测量技术通过两束相干光叠加产生的干涉图案求解光波相位信息，但其对环境的要求高，高相干光的散斑噪声也极大地限制了其应用范围。衍射相位测量技术的经典手段是相干衍射测量［12-13］，通过测量透过样本光波的衍射图案，在施加各种约束的情况下，以逆源算法求解出样本的相位信息。但求解的约束条件一般远小于求解相位的数量，问题的病态程度十分明显，求解过程也不稳定。

传统显微成像技术存在的问题无疑减缓了人类对微观世界的探索进程，亟需一种可以同时实现大视场、高分辨率和定量相位成像的显微技术。随着计算机技术的发展，计算光学成像技术问世［14］，其通过建立系统照明、集光和成像3 个模块的数学模型，并结合人为引入的先验条件，如照明模块的光强、相位和偏振调制等，可以使用计算机从拍摄的二维光强图像中重建出样本的复振幅透过率、3D 折射率分布等信息，打破了传统显微成像技术“所见即所得”的成像模式。

2013 年提出的傅里叶叠层显微术［15-17］（Fourier Ptychographic Microscopy，FPM），因为引入先验知识的巧妙性和成像性能的优越性，成为了极具发展潜力的计算光学成像技术。FPM 系统的搭建十分简单，只需要将现有显微系统的照明光源替换为可变角度的光源，例如可编程LED 阵列［15］、数字微镜（DMD）器件［18］、扫描振镜［19］等。FPM 一般先通过具备大视场特性的低倍显微物镜采集一组不同照明角度的光强图像作为原始数据集，随后通过合成孔径［20］和相位恢复［9］算法，将采集的图像拼接融合，在保留低倍显微物镜大视场特性的前提下，得到了接近衍射极限的高分辨率复振幅图像。FPM 自问世以来，因为其优越的性能和简单易行的实现方式，受到了广泛的关注，得到了快速的发展，如今已经被应用到数字病理［21］、血细胞计数［22-23］、3D 成像［24-26］等多个领域。

作为一种计算光学成像技术，FPM 重构图像质量的高低很大程度上取决于重构算法采用的数学模型与实际系统的匹配度。在重构样本信息时，FPM 将每一张采集图像的振幅作为空域的模值约束，将其频谱用于更新与照明角度对应的子频谱区域。在融合完所有的采集图像后，重构图像频谱的支持域会得到拓展，从而提高成像分辨率。在更新频谱的过程中，每个子频谱的位置与照明角度需要完全对应，否则重构频谱将发生畸变，所导致的伪影会降低重构图像的质量。

在经典的FPM 系统中，通常使用一个可编程控制的LED 阵列作为照明光源提供变角度照明。在安装误差仅几微米的现代装配工艺下，可以认为LED 阵列被规则地排布在一个刚体上，每个灯的位置可以根据排布规则计算得到。但在安装、调节、更换LED 阵列时，LED 板的位姿却很难调到理想位置，不可避免地会出现平移、旋转和倾斜位姿偏差。如果仍然依据理想的LED 位姿计算，不匹配的子频谱位置必将造成重构图像质量的下降。为此，围绕LED 阵列位姿校正的研究得到了广泛关注，且发展迅速，成果显著。经典的机械校正法利用多自由度的精密机械调节台，可以直接将LED 阵列调节到理想位置［27-28］，从源头上解决位姿不匹配的问题。但这类方法存在诸多问题，除了精密机械调节台导致的系统体积大与成本高之外，调节LED 阵列到理想位姿这一过程对使用者也有较高的要求，通常需要了解光学系统的旋转对称特性并依赖水平仪等额外设备才能实现位姿校准。此外，该类方法对系统变化也很敏感，在更换显微物镜或者移动系统之后就需要再次校准。

为了避免机械校正法的问题，许多研究者利用采集图像间接地计算照明角度，提出了诸多的数据驱动校正方法。在这些方法中，基于模拟退火［26-33］（Simulated Annealing，SA）的搜索算法最先被提出并快速发展，基于粒子群优化［34-36］（Particle Swarm Optimization，PSO）的搜索算法也得到了一定的关注。除了搜索算法外，梯度下降法［37-38］和明场频谱定位法［39-40］的有效性和可行性也得到了验证，也有研究者采用机器学习的方法克服了位姿偏差的问题［41-43］。但是，直接从拍摄图像的强度或频谱信息得到位姿参数的庞大计算量会减缓成像速度，系统的像差［44-48］、噪声［49-50］和照明光强波动［51-52］所导致的图像变化也会与位姿偏差导致的图像变化相互耦合，从而降低数据驱动校正法的精确度。近年来，本课题组也围绕位姿校正问题开展了一系列的工作，除了改良的机械校正法［27］和机器学习法［41］外，我们针对数据驱动校正法的问题，提出了两种基于光学系统成像机制的校正方法，可以根据拍摄图像中易于检测的几何变化量来计算精确的照明角度，计算依据分别是离焦图像的偏移量［53］和采集图像中明暗场边界的几何参量［54］。

本文对FPM 系统的光源位姿校正问题进行了系统的综述：简述了FPM 的基本原理，并对光源位姿偏差的影响进行了定量的比较和分析。介绍了机械校正法的基本原理、实现方式和优缺点。详细介绍了以SA 算法为代表的搜索算法的基本原理、发展历程和优缺点，并给出了梯度下降法、明场频谱定位法和机器学习法3 类数据驱动校正法的基本原理和优缺点。阐述了基于系统成像机制的两种代表性方法的基本原理和实现方式，并说明了该类方法的优势。最后，对照明光源位姿校正问题进行了总结和展望。

2 FPM 系统中的位姿偏差

2.1 FPM 的基本原理

FPM 系统可以在现有的显微系统上直接搭建，只需要将照明光源替换为可编程LED 阵列即可，如图1（a）所示。从系统结构而言，FPM 系统通常包含图1（b）所示的可编程LED 阵列、低数值孔径（Numerical Aperture，NA）物镜、筒镜和相机。在采集作为原始数据集的低分辨率（Low Resolution，LR）图像时，将LED 单元依次打开，并利用相机采集对应的LR 图像。如果LED 阵列距离样本足够远，且LED 灯的发光面积足够小，就可以认为第m行、第n列的LEDm，n单元发出平面光波，相机采集的强度图像可以表示为

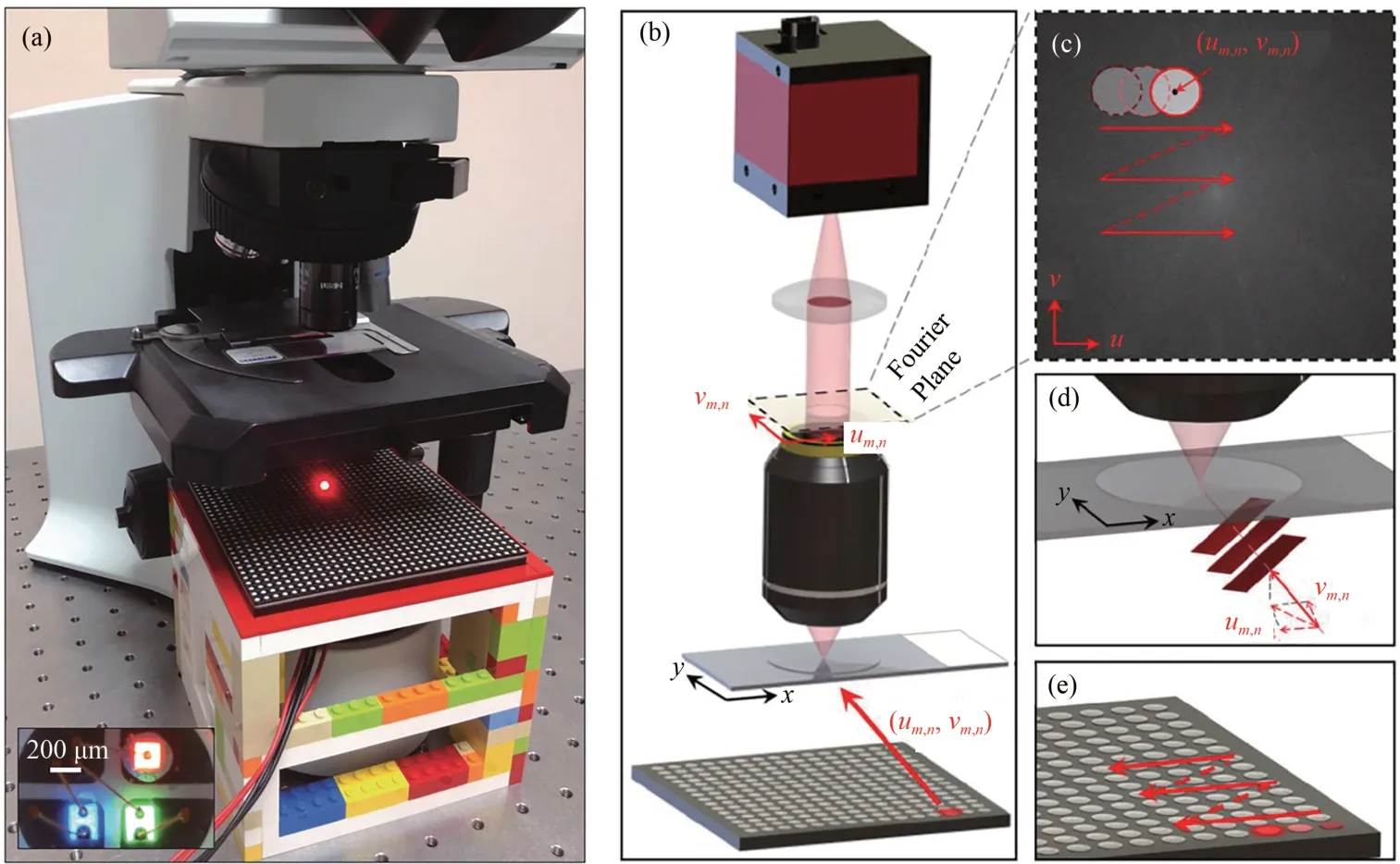
图1 傅里叶叠层显微系统和工作原理图。（a）傅里叶叠层显微系统实物图［15］；（b）傅里叶叠层显微系统结构图［16］；（c～e）傅里叶叠层显微术的工作原理。Fig.1 System setup and principle of FPM.（a）System setup of FPM［15］；（b）System configuration of FPM［16］；（c～e）Imaging principle of FPM.

其中：o(x，y)是样本的复振幅透过率，p(x，y)是系统的点扩散函数，i是单位虚数，(x，y)是二维空域坐标，（um，n，vm，n）是光波矢，⊗表示卷积运算，O(u，v)是样本的频谱，P(u，v)是系统的光瞳函数，(u，v)是二维空间频率域坐标，ℑ-1｛｝表示逆傅里叶变换运算。

式（1）表明，相机采集到的图像在频域内是样本频谱O(u，v)和光瞳函数P(u，v)相乘的结果。当采用倾斜照明时，图像频谱会发生与照明波矢（um，n，vm，n）相对应的平移。所以，当采用图1（e）所示的一系列不同位置的LED 灯照明时，可以对不同位置的子频谱进行扫描采集，如图1（c）所示。从数学上来说，照明波矢（um，n，vm，n）可以表示为

其中：λ是照明光波的波长，(x0，y0)是样本的子区域中心位置坐标，(xm，n，ym，n，zm，n)表示LEDm，n的位置坐标，h是LED 阵列到样本之间的距离。

在采集完LR 图像数据集后，FPM 结合系统的数学模型与先验知识，通过重构算法迭代恢复出具有大视场和高分辨率（High Resolution，HR）特性的样本复振幅图像。为保证算法收敛，整个重构过程需要进行J次迭代，每一次的迭代过程可以分为图2所示的5个步骤。（1）初始化样本的频谱和系统的光瞳函数，记为Oj(u，v)和Pj(u，v)。初始的样本频谱可以是一张过采样的LR 图像的傅里叶频谱，也可以采用随机的频谱估计。初始的光瞳函数通常被设置为一个圆形的低通滤波器，在通带内振幅是1，在通带外振幅是0，通带内外的相位都是0。（2）给出LEDm，n照明时的LR 图像估计。由第一步给出的Pj(u，v)和Oj(u，v)，将当前LR 图像的傅里叶频谱估计计算为(u，v)=Oj(u-um，n，v-vm，n)Pj(u，v)，对其进行逆傅立叶变换得到LR 图像的估计（3）用相机拍摄的LR 图像替换LR 图像的估计，得到更新后的LR图像：

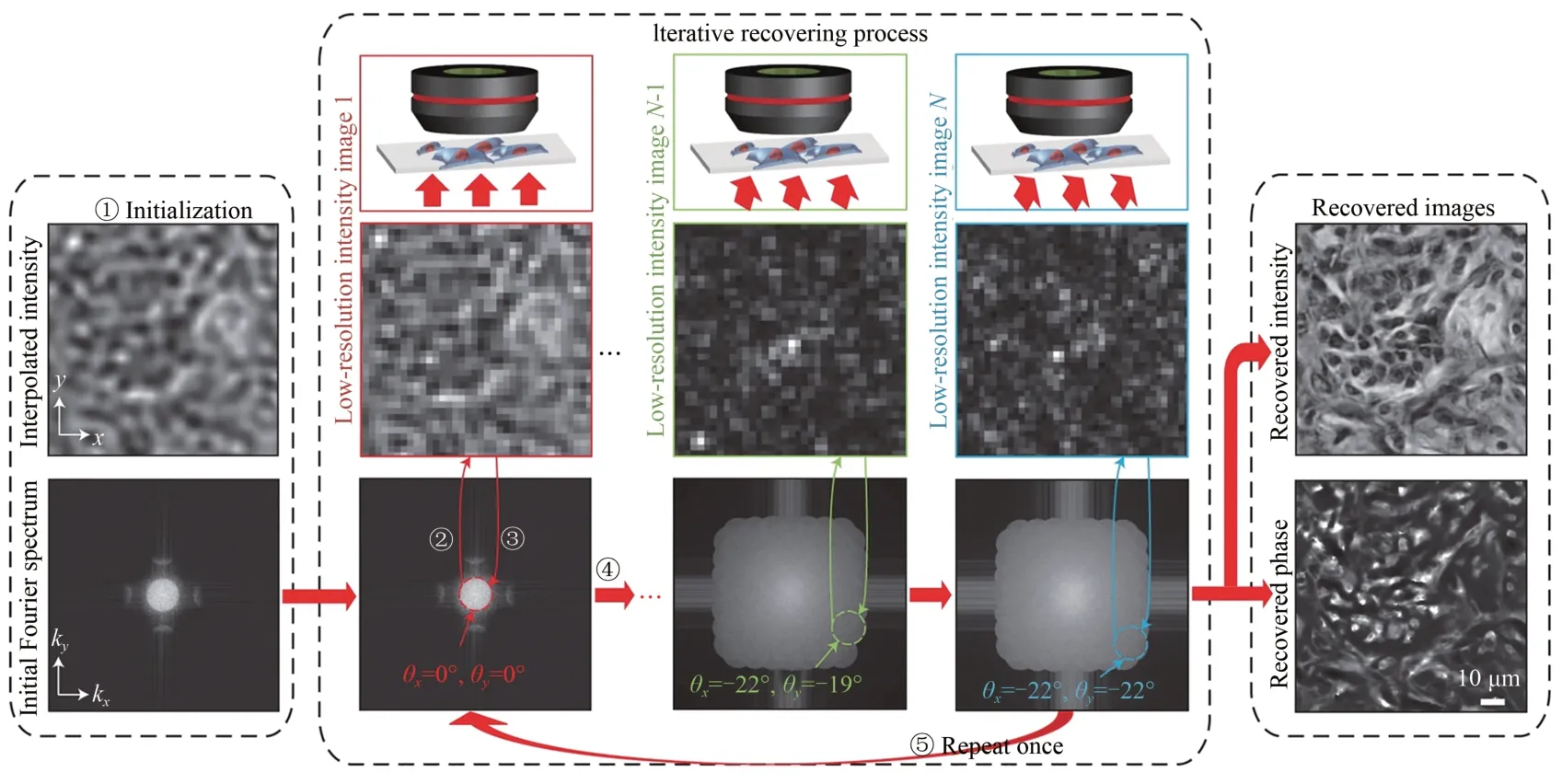
图2 傅里叶叠层显微术的重构流程［15］Fig.2 Reconstruction flow chart of FPM［15］

其中：*为复共轭运算，δ1和δ2是用来防止分母为零的规范化常数，j是当前迭代的次数，ΔΦj，m，n是更新过程的误差辅助函数：ΔΦj，m，n=（4）用步骤（2）和（3）处理其余照明角度的图像，直到所有拍摄的LR图像都被处理完毕。（5）整个迭代过程重复多次，直到重构结果收敛。在重构算法结束后，样本频谱的支持域将被极大地拓展，再通过傅里叶变换到空域即可得到HR 的强度和相位图像。

2.2 位姿偏差的影响及评价

值得注意的是，重构得到高质量的样本图像有一个重要前提，在选取图2 中圆形区域所示的子频谱时，其位置必须与实际的照明波矢相对应。式（2）表明，LED 灯与样本的相对空间坐标直接决定对应子频谱的中心坐标，能否精确地定位LED 灯的位置直接影响重构图像的质量。如果重构算法中LED 灯的位置与实际位置不一致，则会在重构图像中引入伪影，影响对样本信息的观测。然而，在搭建FPM 系统时，需要相当繁琐的步骤才能将LED 阵列调节到预定的位姿，LED 阵列的位姿还有可能在后续的实验中因为碰撞或更换系统零件而发生改变。所以，对LED 阵列的位姿进行校正成为了重要的研究工作。

在实际成像过程中，往往需要数十甚至上千个LED 灯进行照明，直接测量数量如此庞大的LED灯位置是一件相当费时费力的工作。不过，LED阵列的排布规则为解决这个问题提供了重要的先验知识。现有的或定制的LED 阵列一般都是在一块基底上按照某种规则排布LED 灯，比如方阵排布［15］、环形排布［55］和穹顶排布［56］，这些排布规则使位姿校正问题的未知量急剧减少。以经典的方阵LED 阵列为例，想要获得每个LED 灯的位置，只需要求解图3 所示的6 个位姿参数，其中，z轴是物镜光轴，Δx和Δy分别是LED 阵列沿着x轴和y轴的横向偏移量，θz是LED 阵列绕着z轴的旋转角，θx和θy分别是LED 阵列绕着x轴和y轴的倾斜角，h是样本到x-o-y面的距离。只要知道了这6 个位姿参数，就可以求解每一个LED 灯的坐标为

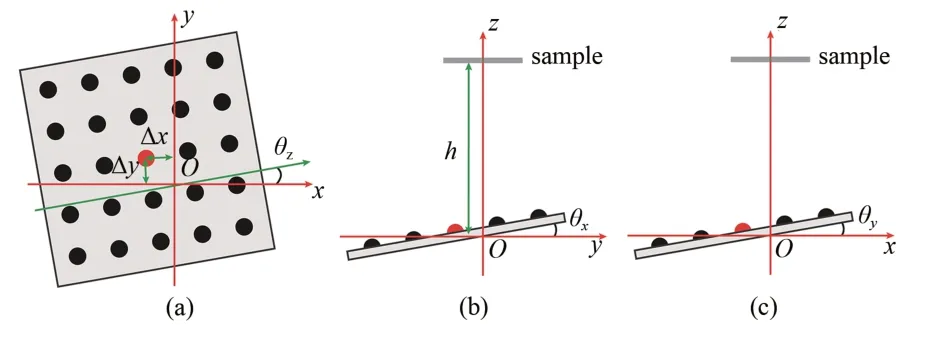
图3 LED 阵列的位姿偏差［54］Fig.3 Pose misalignment of LED array［54］

其中：dLED是相邻LED 灯之间的距离，R是旋转矩阵，可以表示为

在得到LED 灯的位置坐标(xm，n，ym，n，zm，n)后，就可以根据式（2）计算对应的照明波矢，即子频谱的中心位置坐标。如果所采用的6 个位姿参数和实际系统参数一致，则子频谱的中心位置完全正确，就能恢复出高质量的样本图像。否则，子频谱的错位将导致重构图像中出现伪影，降低重构图像的质量。不同的位姿参数的影响有所不同，下面将定量分析各个位姿偏差对重构图像的影响。

（1）横向偏移量对重构图像的影响。因为Δx和Δy的差异只取决于对坐标轴的定义，故只需要分析Δx即可。图4（e1）展示了当Δx从0 增加到2 000 μm 的过程中，441 个子频谱的实际位置和理想位置相差的像元数总和Δp的变化曲线，Δp和Δx呈近似线性关系。不过，仅利用Δp作为评价指标还不足以说明位姿偏差的影响，因为相比于频域内的样本频谱而言，空域内的样本强度和相位图像更能表征样本的吸收和折射性质。图4（e2）展示了相同的横向偏移量下，重构强度图像与样本强度图像之间的均方根误差（Root-Mean-Square Error，RMSE）曲线，图4（e3）展示了相位的RMSE 曲线。有趣的是，RMSE 曲线不是线性变化的，而是呈现出一种阶梯状的增长方式。例如，当Δx从600 μm 变到700 μm 时，强度和相位的RMSE 值都剧增，重构图像中出现了明显的伪影，分别如图4（b1）和（b2）所示。空域的RMSE 曲线和频域的Δp曲线增长方式的差异，是重构图像中的伪影和不同位置的子频谱对LED灯位置变化的响应不同所导致的［37］。换句话说，如果不同位置的子频谱的响应一致，位姿偏差就只会导致整个频谱平移，此时只需要根据傅里叶变换的平移不变性质，在空域内添加一个共轭相位因子就能消除伪影，即能够在Δp值很大时获得很小的RMSE 值。

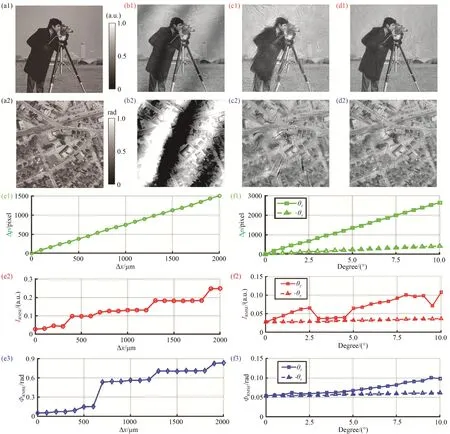
图4 位姿偏差对重构图像质量的影响［54］。（a1～a2）样本强度和相位图像；（b1～b2）横向偏移量为700 μm 时的重构强度和相位图像；（c1～c2）绕z 轴旋转角为10°时的重构强度和相位图像；（d1～d2）绕y 轴倾斜角为10°时的重构强度和相位图像；（e1～e3），（f1～f3）所有子频谱实际位置和理想位置相差的像元数总和Δp、重构强度图像与样本强度图像的均方根误差、重构相位图像与样本相位图像的均方根误差与横向偏移量Δx，旋转角θz，倾斜角θy 的关系曲线。Fig.4 Effects of pose misalignments on the quality of reconstructed images［54］.（a1～a2）Intensity and phase images of sample；（b1～b2）Reconstructed intensity and phase images when the lateral shift Δx equals to 700 μm；（c1～c2）Reconstructed intensity and phase images when the rotation angle along z-axis equals to 10°；（d1～d2）Reconstructed intensity and phase images when the tilt angle along y-axis equals to 10°；（e1～e3），（f1～f3）Curves of the pixel number difference between all ideal and true sub-spectra，RMSE between reconstructed and true intensity images of sample，RMSE between reconstructed and true phase images of sample，versus as the lateral shift Δx，rotation angle θz，and tilt angle θy.

（2）旋转角θz以及倾斜角θx和θy对重构图像的影响。同样地，因为θx和θy的影响完全一致，只需要分析θy即可。图4（f1）展示了当旋转角θz和倾斜角θy从0 增加到10°的过程中，Δp的变化曲线。从频域上来说，Δp也近似线性变化，且θz的影响远大于θy。但从空域上来看，θz和θy的影响差距并不大，强度和相位的RMSE 曲线都保持在0.1以下。此外，θz和θy的影响可以认为小于Δx的影响，因为即使它们达到了裸眼都可以轻松看出的10°，在重构图像中仍然能分辨样本的信息，如图4（c1～c2）和（d1～d2）所示。

（3）h对重构图像的影响。为了确保LED 灯能被认为是点光源，LED 阵列与样本之间的距离一般很大，可以忽略掉测量误差，故h对重构图像的影响没有其他5个参数明显。但FPM 作为一种定量成像技术，为了保证成像的准确性，任何一个位姿偏差都不应被忽略。

3 机械校正法

经典的位姿校正方法是使用精密机械将LED 阵列调节到理想的位置。图5 展示了机械校正法的原理，图5（a）是一台利用奥林巴斯倒置IX73 显微镜搭建的FPM 系统，为校正位姿偏差，利用立柱和螺栓将LED 阵列固定，并利用水平仪装配，确保无旋转和倾斜偏差，如图5（b）所示。安装完毕后，先用二维机械平移台将LED 阵列移动到图5（c）所示的4 个边缘位置并记录坐标，再将LED 阵列调回坐标的中点，利用光学系统的对称性消除了横向偏移偏差［28］。

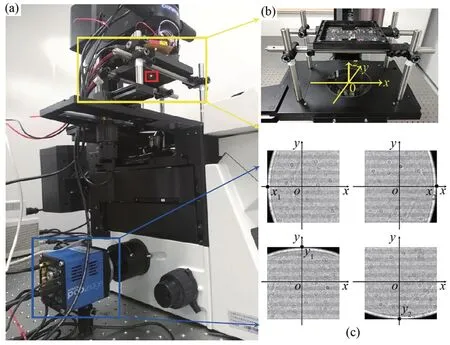
图5 精密机械校正位姿偏差的原理示意图［28］。（a）系统示意图；（b）旋转与倾斜偏差校正；（c）横向偏移偏差校正。Fig.5 Principle of pose calibration with precision mechanical stages［28］.（a）System configuration；（b）Calibration of the rotation and tilt misalignments；（c）Calibration of the lateral shift misalignments.

上述方法为了消除旋转偏差，采用了大量额外的机械配件，导致系统的体积和装调成本增加。本课题组利用远心物镜搭建了一套小型的FPM 实验装置，并提出了一种改进的机械校正方法［27］。如图6 所示，在校准横向偏移前，先调节LED 阵列和远心物镜的相对位置，使得相机拍摄对焦的LED 阵列，以视场内多个LED 灯的排布线是否与相机的坐标轴方向一致作为判据，可以调节实现o1x1和o2x2共面，o1y1和o2y2共 面，达到消除旋转偏差的目的。如果相机拍摄的LED 阵列图像如图6（b1）所示，LED 灯的排布线（图中虚线）与相机坐标轴方向（图中实线）存在夹角，说明LED 阵列存在旋转偏差，需要利用旋转台调整LED 阵列，直到相机拍摄的图像如图6（b2）所示时，旋转偏差被消除。随后，再利用光学系统的对称性消除其余位姿偏差，完成位姿校正。

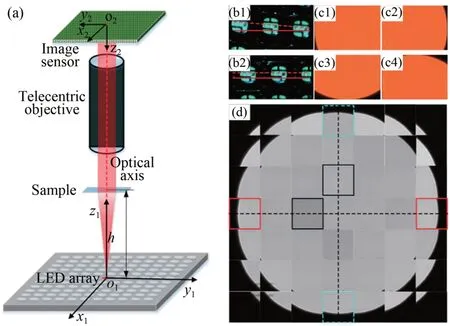
图6 改进的机械校正法［27］。（a）系统示意图；（b1～b2）旋转偏差校正；（c1～c4）横向偏移偏差校正；（d）反映光学系统对称性的孔径光阑强度图。Fig.6 Improved mechanical calibration method［27］.（a）System configuration.（b1～b1）Calibration of the rotation misalignment；（c1～c4）Calibration of the lateral misalignments；（d）Intensity images of the aperture stop that imply the centrosymmetric characteristic of the optical system.

4 数据驱动校正法

针对FPM 系统中LED 阵列的位姿校正问题，以拍摄图像强度或频谱信息为驱动自动求解位姿参数的方法，本文中称为数据驱动校正法。根据校正原理的不同，可以将其分为搜索算法、梯度下降法、明场频谱定位法和机器学习法。

4.1 搜索算法

FPM 本质上是叠层成像［57-58］（Ptychographic Iterative Engine.PIE）的傅里叶对偶形式。在PIE中，为了保证重构图像的质量，多种用于获取照明探针位置的搜索算法被提出，包括遗传算法［59］、SA 算法［60］以及全局漂移模型［61］等。而在FPM 中，基于SA 算法和PSO 算法的搜索算法的可行性也得到了验证，其中，SA 算法最早被用于校正LED 阵列的位姿偏差。SA 算法是在有限空间内搜索未知变量，使得损失函数的值最小，其优势是不需要考虑所有可能的情况，只需要搜索几个方向即可。

在FPM 中，SA 算法需要在傅里叶频域内几个特定的方向搜索子频谱的正确位置，流程一般分为4 步。（1）初始化子频谱位置(um，n，vm，n)，搜索方向的数量R和搜索步长(Δur，m，n，Δvr，m，n)；（2）利用初始化参数给出一组子频谱序列：

其中：r=1，2，…，R是一个搜索方向，(Δur，m，n，Δvr，m，n)是第r个方向的搜索步长；（3）确定最恰当的搜索方向和子频谱位置，用于评价搜索方向正确性的损失函数为

（4）减小搜索步长(Δur，m，n，Δvr，m，n)，并重复第（2）、第（3）步，达到终止条件时，认为子频谱位置与实际位置一致。

2015 年，SA 算法首次被用于校正FPM 系统中的LED 阵列位姿误差［29］，图7（a）给出了校正前后的照明NA。可以看出，直接将SA 算法用于校正位姿偏差存在2 个主要问题：（1）对大照明NA 的校正误差大。当照明NA 大于物镜NA 时，拍摄的图像是信噪比较低的暗场，用E（r）作为评价指标的误差较大；（2）校正后的照明NA 分布混乱，与实际的LED 灯排布不符合。此外，该方法也极其耗时，由于在每一次迭代中都要校正每一个LED 灯的位置，FPM 的成像速度也降低了10 倍以上。

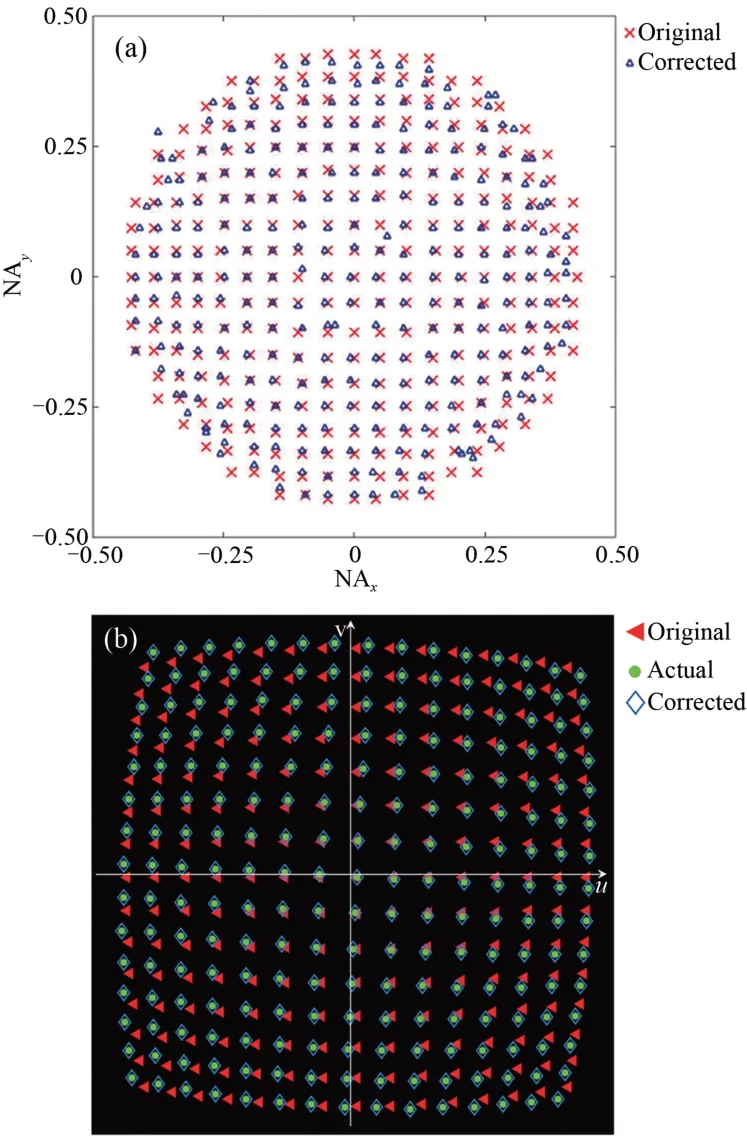
图7 基于SA 算法的搜索算法校正结果。（a）常规SA 算法［29］；（b）pcFPM 方法［30］。Fig.7 Calibration results of SA-based search algorithms.（a）Conventional SA algorithm［29］；（b）pcFPM method［30］.

为了解决常规SA 算法的问题，Sun 等人在2016年提出了pcFPM 方法［30］。针对校正后子频谱排布混乱的问题，pcFPM 在SA 算法更新子频谱位置后，利用实际LED 阵列的排布规则增加了一个非线性约束过程：

其中：(Δx，Δy，θz，h)用来表征LED 阵列排布规则的4 个位姿参数，Q(Δx，Δy，θz，h)表示SA 算法得到的子频谱和LED 排布规则的差距，当这种差距最小时，得到的(Δx，Δy，θz，h)u就可以用于表示LED 阵列的实际位姿。通过添加非线性约束的过程，校正后的子频谱符合实际的排布规则，如图7（b）所示。

此外，针对常规SA 算法耗时长的问题，pcFPM 给出了一种新的迭代策略。常规SA 算法每次迭代都要校正每一个子频谱的位置，显著降低了成像速度。pcFPM 舍弃了这种迭代策略，在前几次迭代时只校正信噪比较高的明场子频谱位置，得到一个相对合理的初始值，然后在后续的迭代中引入暗场子频谱，对全局的位姿进行估计。这种迭代策略减少了搜索的时间损耗，例如，对包含25 个明场照明灯的225 个灯的位姿校正时，如果总迭代次数为12 次，在前9 次迭代中只校正明场子频谱，那么总的时间消耗约为常规SA 算法的1/3。

虽然pcFPM 方法在一定程度上解决了常规SA 算法的问题，但也还存在两个问题：（1）当LED阵列位姿偏差很大时，pcFPM 方法可能会陷入局部最优解，甚至无法收敛。虽然可以通过增大搜索步长和搜索方向数量在一定程度上解决这个问题，但这也会进一步增加计算时间；（2）pcFPM 方法对初始参数敏感，需要对实际位姿偏差有一个较好的初始估计，才能保证算法的精确度。

4.2 梯度下降法

除了搜索算法之外，梯度下降也能校正位姿偏差。2017年，基于牛顿法的二阶梯度下降法的有效性得到了验证［37］。与常规的梯度下降算法一样，其通过求误差矩阵对未知量的偏导数来确定未知量。在FPM 中，误差矩阵为

用牛顿法校正位姿偏差具有一定的可行性，但是因为牛顿法固有的局限性：（1）海森矩阵的计算非常耗时；（2）牛顿法只是局部搜索算法，极易陷入局部最优，牛顿法只能说提供了一个新的位姿校正思路。之后，针对牛顿法的两个问题，采用遗传算法提供全局估计，再使用拟牛顿法近似计算海森矩阵的方法得到了验证［38］。该方法确实解决了局部收敛问题，校正的横向偏移偏差可以达到几个毫米，但是遗传算法所增加的时间和拟牛顿法所减少的时间相比，是否有优势并没有得到验证。

总的来说，梯度下降法虽然可以解决一般性的优化问题，但是在FPM 中，多张图像、多次迭代中计算梯度所增加的时间损耗使梯度下降法在计算资源有限的情况下，实用性并不大。

4.3 明场频谱定位法

除了构建损失函数和误差矩阵求解子频谱位置外，还有一种可以定位子频谱位置的频谱分析法。频谱分析法是对采集强度图像的频谱进行分析，试图从中找到解决问题的方案，曾被用于确定衍射图案中心来校正系统［60-61］。在FPM 中，明场频谱定位法［39］是一种用于校正子频谱位置的频谱分析法。对式（1）给出的采集图像强度分布做傅里叶变换，可以得到采集图像的频谱为

其中，★表示自相关运算。式（14）表明，采集图像的频谱数学上是由两个相同的圆形区域O(uum.n，v-vm，n)·P(u，v)在频域内扫描相乘得到。

一般而言，样本频谱的振幅图像中存在一个极强的零频直流量，其余频率分量的振幅会随着频率增大而快速衰减。随着照明光角度的变化，直流量将会平移到点(um，n，vm，n)，如果该点处于光瞳通带内，为明场照明，反之，则为暗场照明。在明场照明时，作自相关运算的圆形频谱半径为频谱振幅在点(um，n，vm，n)有极大值且随着频率增大而快速衰减。两个这样的频谱作相关运算的结果，就是拍摄图像的频谱中出现两个分别以(um，n，vm，n)和(-um，n，-vm，n)为圆心，以为半径的圆形区域，如图8（b）所示。这一现象意味着，只需要在拍摄图像频谱内找到这样的两个圆的位置，就能确定子频谱的位置。

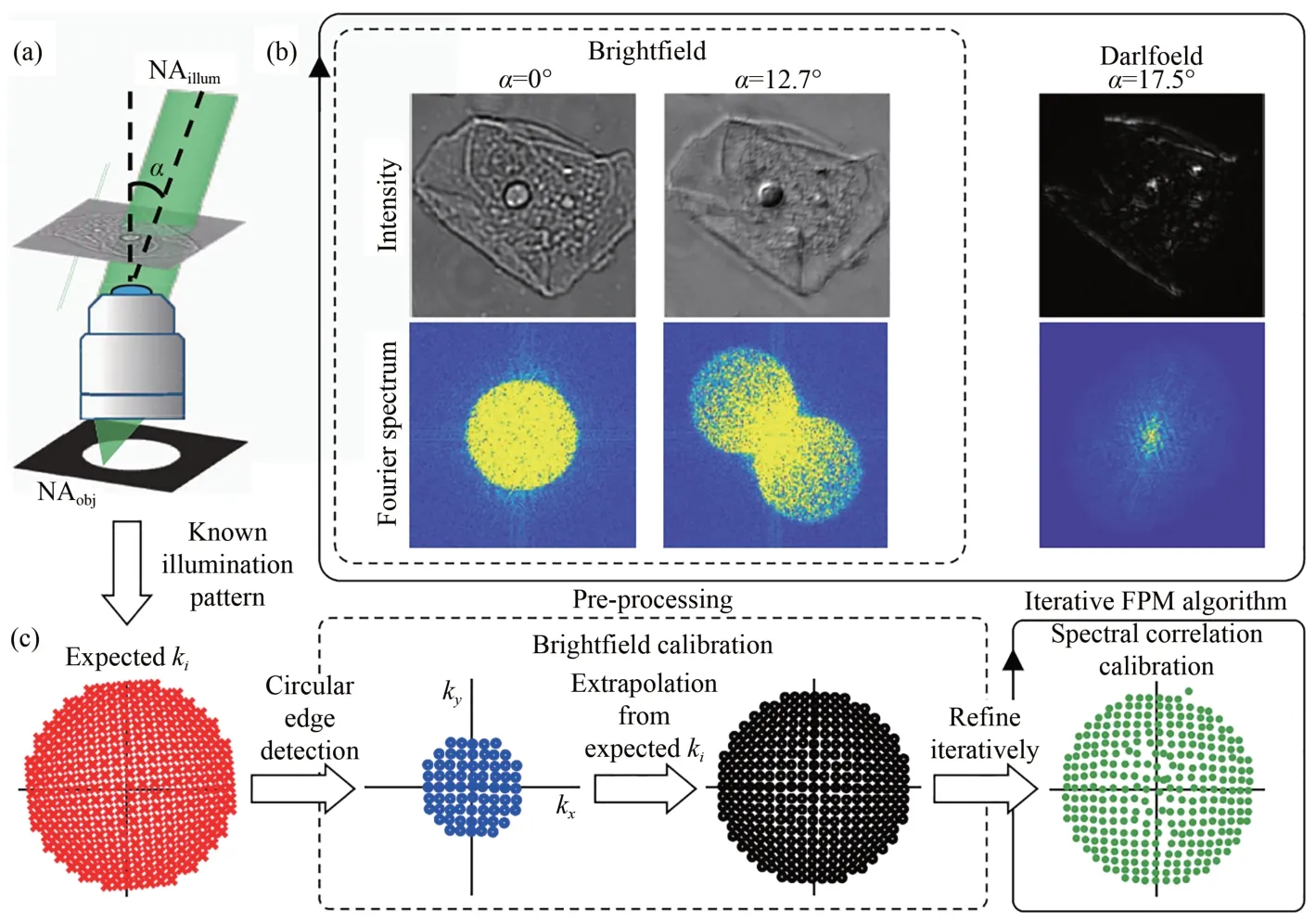
图8 明场频谱定位法的原理［39］。（a）倾斜照明示意图；（b）明场图像频谱和暗场图像频谱；（c）预处理与全局位姿校正。Fig.8 Principle of brightfield spectral localization method［39］.（a）Illuminating a sample with an oblique angle а；（b）Spectra of brightfield and darkfield images；（c）Pre-processing and global pose correction.

不过，频谱定位法只对明场图像有效，因为对于暗场图像而言，点(um，n，vm，n)已经落到了光瞳通带外，采集图像频谱并不会出现与明场频谱一样的特性。因此，明场频谱定位法通常用作预处理，然后再通过LED 阵列的排布规则扩展得到暗场子频谱的位置，最后通过其他的校正方法得到最终的子频谱位置［40］，如图8（c）所示。

该方法对平板LED 阵列、穹顶式LED 阵列和扫描振镜照明的FPM 系统的位姿校正都有效，但是，也存在两点问题。（1）该方法计算时间较长。如果只对明场校正，额外的几十秒时间是可以接受的，但加上了暗场校正步骤，额外的上百秒计算时间无疑又降低了成像速度；（2）该方法难以实现全视场的或某些特殊照明角度的位姿校正。在视场图像的某些区域，或者当照明NA 接近物镜NA 时，拍摄的图像同时包含了明场和暗场，该方法将不再适用。

4.4 机器学习法

近几年，受机器学习成功求解病态反演问题的启发，一些研究人员将机器学习方法引入到FPM 的研究中，利用神经网络模型克服LED 阵列位姿偏差所引起的问题。在机器学习中，传统的监督学习方法的训练过程是将真实基准与模型输出结果进行对比，通过二者的误差对模型进行迭代更新，但由于FPM 观测样本的多样性与LED 阵列位姿偏差的复杂性，有监督学习下数据集的建立异常困难，并且随着样本特征的改变，有监督学习下训练出的神经网络对位姿偏差预测的置信度将受到挑战。无监督学习通常没有一个与输入数据相匹配的基准，而是通过输入数据自身对模型的参数进行更新，因此，利用无监督的机器学习方法解决位姿校正问题引起了研究人员的关注。

Zhang 等人在2020 年提出了一种用于校正LED 阵列位姿偏差的前向成像神经网络FNN-CP［42］。如图9 所示，该方法直接将FPM 的前向传播过程建模成神经网络的形式，每一层都代表一个具体的前向传播过程，样本的频谱和(Δx，Δy，θz，h) 4 个位姿参数都被视为层中的可学习权重。通过最小化训练过程中的损失函数，可以根据训练的位姿参数校正位姿偏差，还可以将样本的傅里叶频谱和不同Zernike 模式的系数设置为神经网络层中的可学习权重，用于校正物镜的像差，也可以部分补偿由LED 阵列位姿偏差对重构的样本的傅里叶频谱造成的影响。

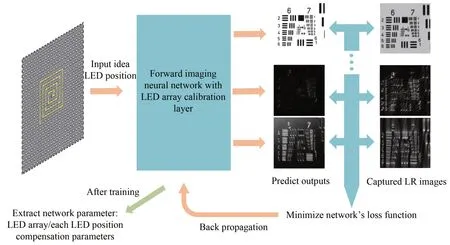
图9 傅里叶叠层显微术中用于LED 阵列位姿校正的机器学习法Fig.9 Machine learning method for calibrating pose misalignment of the LED array in FPM

除了将位姿参数作为学习权重之外，还有一种用于校正每一个LED灯位置的无监督学习方法［43］。该方法直接以样本的复振幅透过率作为重构对象而非样本的傅里叶频谱，结合LED 阵列中不同LED 的位置与物镜推算出系统的点扩散函数，利用两者的卷积构建FPM 的前向成像神经网络模型。该模型引入了用于描述每个LED 位置偏差的可学习权重，使神经网络在训练过程中直接重构样本的复振幅透过率信息与每个LED具体位置。但由于该方法在建模过程中选择了用卷积的方式构建前向成像模型，随着重构样本的图像尺寸增大，该方法优化所需要的时间将大幅增加。

尽管机器学习方法在LED 位姿校正方面的研究和应用较少，但机器学习方法仍旧展现出了一些性能上的优越性。如果可以对FPM 成像过程中的多种偏差进行综合校正，对每个LED 做独立的位置校正而无需严格的假设，机器学习法仍是一类有前景的位姿校正方法。

5 成像机制校正法

从本质上来说，上述的4 类数据驱动校正法都是利用采集图像所包含的样本信息求解子频谱位置，但除了LED 阵列的位姿偏差外，照明光的强度波动、噪声以及像差等其他系统误差都会影响采集的样本信息，数据驱动校正法难以从多种系统误差中分离出准确的位姿参数。为解决此问题，我们课题组尝试直接从显微系统的物理成像模型出发，利用系统的本征特性来校正位姿偏差，提出了离焦校正法［53］和出瞳校正法［54］。这两种方法不仅可以解耦得到准确的位姿参数，还可以将它们和针对其他系统误差的校正方法联合使用。

5.1 离焦校正法

离焦校正法利用离焦图像的特性求解位姿参数并获取子频谱位置。当样本离焦时，采集的强度图像变为

其中，H(u-um，n，v-vm，n，zdefocus)是描述离焦图像和对焦图像关系的相位因子，可以表示为

其中：Mag 是系统的放大倍数，zdefocus是离焦距离。在傍轴近似条件下，可以得到：

第一项表明，相比于对焦图像而言，离焦图像会发生平移；第二项表明，离焦图像的质量会变差。

离焦校正法的基本原理可以用式（17）中的第一项描述：当样本离焦时，采集图像会随着照明光波矢的变化而平移，沿着x和y方向的平移量分别为

式（18）表明，如果离焦距离zdefocus固定，那么子频谱位置(um，n，vm，n)就可以通过测量离焦图像的平移量而得到。图10 展示了离焦校正法的一个应用实例。在计算平移量时，通常选取图10（b）所示的中心灯照明的对焦图像作为参考，再计算得到图10（e）所示的明场离焦图像相对于参考图像的平移量。同样地，为了使LED 排布符合实际，离焦校正法也引入了非线性约束过程，计算(Δx，Δy，θz，h) 4 个位姿参数来表征所有LED 灯的位置。

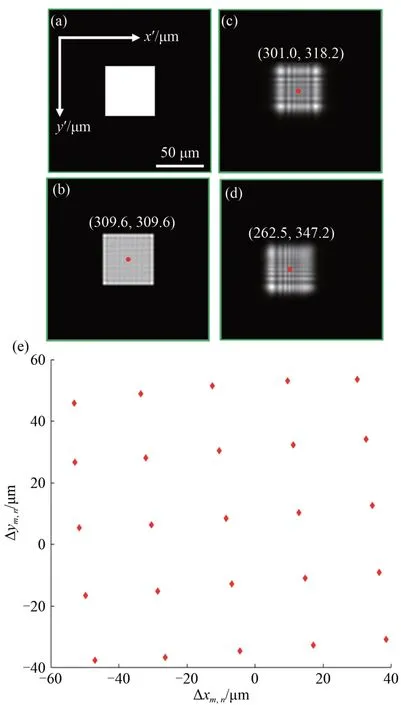
图10 离焦校正法的原理［53］。（a）样本的强度图像；（b）用于参考的对焦图像；（c～d）平移量与照明波矢相关的离焦图像；（e）明场离焦图像的平移量。Fig.10 Principle of defocusing calibration method［53］.（a）Intensity image of sample；（b）Focused image used as reference；（c～d）Defocused images with the shift related to illumination wavevectors；（e）Shifts of the brightfield defocused images.

离焦校正法与数据驱动校正法相比，有两个的优点。（1）离焦校正法所需要的时间极短，不需要任何搜索和迭代。如果只计算图像某个区域的移动量，可以在20 μs 内得到位姿参数，计算时间缩短了3 个数量级以上。（2）离焦校正法的鲁棒性更高，其精确度仅取决于图像的平移量，受到其他系统误差的干扰很小。但该方法也存在一个问题：将样本从对焦位置调节到离焦位置的过程中，调焦旋钮的误差也会导致图像平移，故此方法对调焦旋钮的装调精度要求较高。

5.2 出瞳校正法

相比于离焦校正法，出瞳校正法是一种全自动的位姿校正方法，不需要调焦等预操作，可以直接从采集的LR 图像中求解LED 阵列的6 个位姿参数。在显微系统中，因为光阑的限制作用，采集的图像区域决定于出瞳（孔径光阑）和CMOS靶面（视场光阑）的重叠区域。由于孔径光阑对不同角度照明光的作用不同，这个重叠区域的特性对照明角度的响应存在明显的差异性，意味着可以利用采集图像中这个重叠区域的几何特性求解照明光的波矢，以获得子频谱位置。

图11 展示了出瞳校正法的基本原理。当图11（a1）中所示的中心LED 灯照明时，相机采集到的图像可以用图11（b1）表示，其中红色方框为CMOS 靶面，绿色虚线代表出瞳在CMOS 靶面上的投影（后文简称为“出瞳”），C0，0为出瞳圆心。此时，CMOS 靶面完全位于出瞳内，拍摄图像的整个视场均为蓝色所代表的明场（Bright Field，BF）图像。当图11（a2）所示的照明NA 接近物镜NA 的LED 灯照明时，出瞳圆心从点C0，0移动到点C-1，0，CMOS 的部分靶面位于出瞳外，成为了暗场（Dark Field，DF）图像，图像的整个视场呈现出明暗场共存的分布特性，如图11（b2）所示。在采集的LR 图像中，通常有数十张图像具备这种圆弧状的明暗场过渡边界，出瞳校正法利用了这些边界的圆心和半径，实现了位姿校正。

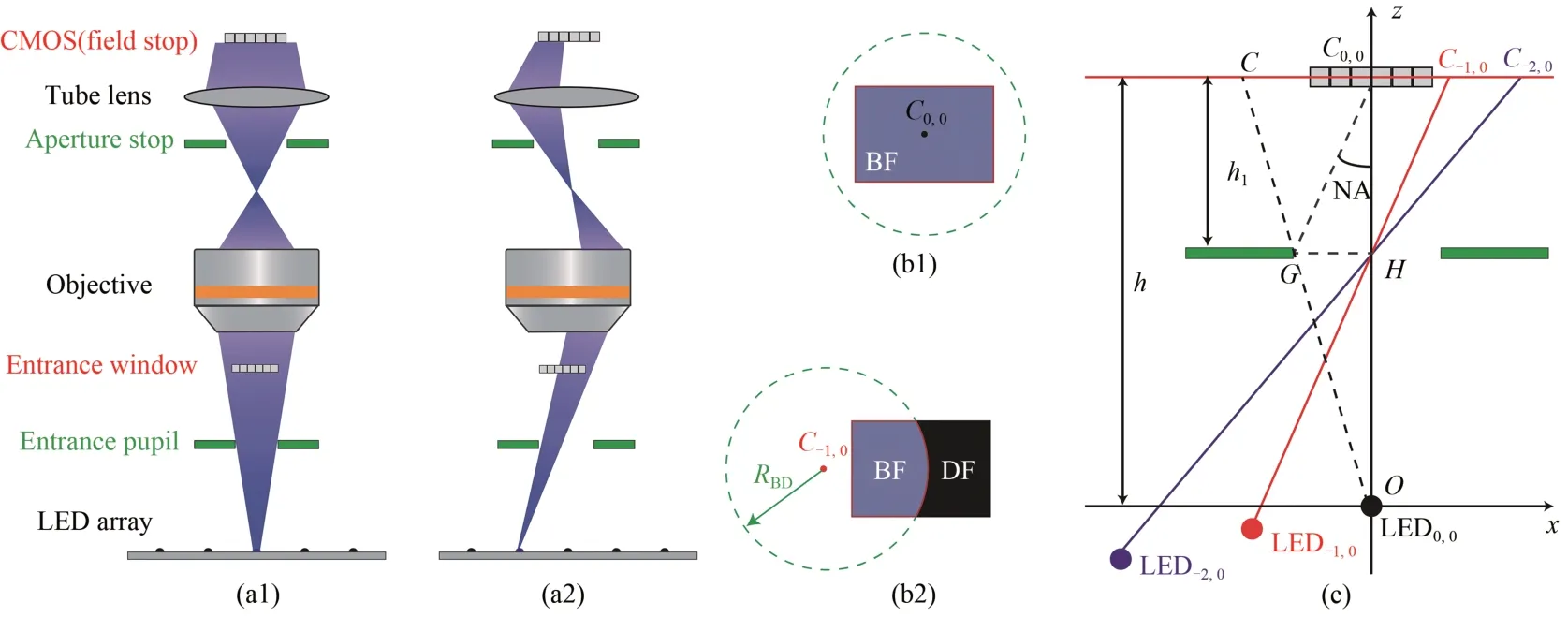
图11 出瞳校正法的原理［54］。（a1）正入射照明；（a2）斜入射照明；（b1）正入射照明采集的图像；（b2）斜入射照明采集的图像；（c）出瞳圆心位置与LED 灯位置的关系。Fig.11 Principle of exist pupil calibration method［54］.（a1）Normal illumination；（a2）Oblique illumination；（b1）Captured image with normal illumination；（b2）Captured image with oblique illumination；（c）Relationship between the position of exist pupil and LED unit.

同计算光学成像原理相似，想要得到子频谱位置，必须先建立物理模型来描述LED 灯的位置与明暗场边界的关系。为便于分析，将显微系统的像空间转换到物空间，如图11（c）所示，GH代表出瞳的共轭面，CC0，0代表CMOS 靶面的共轭面，即样本面。点C0，0、C-1，0、C-2，0代表了圆弧边界的圆心，它们与对应的照明LED 灯的位置存在如下关系：

其中：(xBD，m，n，yBD，m，n)为圆弧边界的圆心坐标，h1是GH与CC0，0之间的距离，可以表示为

其中，RBD是圆弧边界的半径。由式（19）和（20）可知，通过采集图像中圆弧边界的圆心和半径，可以求解出LED 灯的位置(xm，n，ym，n，zm，n)。

图12 展示了出瞳校正法、常规FPM 方法和SA 搜索算法的校正对比图。图12（a）是LED阵列精确对准时的重构图像，图12（b1～b3）、（c1～c3）、（d1～d3）分别是在不同的位姿偏差下用常规FPM 方法、基于SA 算法的SC-FPM 方法［33］和出瞳校正法的重构图像。在位姿偏差较小时，相对于常规FPM 方法而言，SC-FPM 方法重构图像中的伪影几乎都被消除，但是因为其他系统误差的影响，成像对比度较低。当位姿偏差较大时，SC-FPM 方法因为不合适的初始参数，重构图像不再收敛，出现了严重的伪影，如图12（c3）所示。值得注意的是，出瞳校正法在给出的任意位姿偏差下，重构图像都与无位姿偏差时的重构图像相当，这种特性是数据驱动算法所不具备的。

6 总结与展望

傅里叶叠层显微成像术打破了传统光学显微术的限制，能够提供大视场、高分辨率的定量复振幅信息，在诸多领域得到了应用。作为一种经典的计算光学成像方法，重构算法采用的物理模型与实际系统的匹配度是高质量成像的重要保障。为保证高质量的FPM 成像，LED 阵列照明光源的位姿偏差校正问题受到了广泛关注，各种方法被相继提出，且发展迅速。这些方法根据原理的不同，可以分为机械校正法、数据驱动校正法和成像机制校正法。

机械校正法可以从源头上解决LED 阵列的位姿偏差问题，但要求使用者在实验前预校准，费时费力，此外，引入的多自由度精密机械装置也增大了系统的成本和体积。数据驱动校正法旨在消除人为调节的步骤，尝试从拍摄的图像中自动求解出照明角度信息，可以分为以SA 算法为代表的搜索算法、以牛顿法为代表的梯度下降法、明场频谱定位法和机器学习法，这些方法能够在一定程度上校正位姿偏差，但仍然存在校正时间长和校正参数耦合等问题。成像机制校正法通过分析显微系统的成像机制，利用拍摄图像的几何特性校正位姿偏差，不仅校正鲁棒性高，也能够从多种系统误差中分离出准确的位姿参数。

在各类方法中，通过挖掘和利用更简单和清晰的物理模型来解决问题的成像机制校正法，本质上符合计算光学成像的基本特性，是一种极具发展潜力和应用前景的校正方法。但是，目前两种成像机制校正法的作用对象只是明场或明暗场交界图像，若能探索出校正暗场图像的成像机制校正法，FPM 的光源位姿偏差问题将能被更快、更准地解决。