湖北省杉木人工林胸径差分方程及多形地位指数表研究

马羽 许业洲 袁慧 杜超群 邓湘雯

摘要：為解决目前以胸径为指标编制的地位指数表较少，且采用胸径为因子评价立地质量是否可行的问题，选用长期积累的杉木树干解析数据拟合胸径生长方程，构建胸径的差分方程和湖北省杉木人工林地位指数表。运用精度检验和落点检验法分别对导向曲线和地位指数表进行检验与比较，评价其制表精度与适用性。研究结果表明， 1）采用解析木数据拟合胸径的基础方程与差分方程均有良好的拟合优度； 2）选择Korf基础方程与Korf差分方程，以20 a为标准年龄，2 cm为指数级，采用导向曲线法分别编制出湖北省杉木人工林单形地位指数表和多形地位指数表； 3）构建的模型与地位指数表均通过检验，且差分方程的检验精度99.61%，高于基础方程的96.97%；多形地位指数表的落点精度较单形地位指数表高1.18%。由此可见，采用差分方程编制的湖北省杉木人工林胸径地位指数表，较基础方程精度更高，更能准确地评估湖北杉木人工林的立地质量。

关键词：杉木人工林；单形地位指数表；多形地位指数表；胸径生长方程；差分方程；导向曲线

中图分类号：S791.27文献标识码：A文章编号：1006-8023（2023）02-0072-10

Study on DBH Difference Equation and Polymorphic Site Index Table

of Chinese Fir Plantation in Hubei Province

MA Yu1，2， XU Yezhou2*， YUAN Hui2， DU Chaoqun2， DENG Xiangwen1*

（1. College of Life Sciences and Technology， Central South University of Forestry & Technology， Changsha

410004， China; 2. Hubei Academy of Forestry， Wuhan 430075， China）

Abstract：In order to solve the problem that there are few site index tables compiled with DBH as index and the feasibility of using DBH as factor to evaluate site quality， in this study， the DBH growth equation was fitted with the long-term accumulation analytical data of Chinese fir trunks， the difference equation of DBH and the site index table of Chinese fir plantation in Hubei Province were constructed. The accuracy test and point test were used to test and compare the guide curve and the site index table respectively to evaluate the tabulation accuracy and applicability. The results showed that， 1） both the basic equation and the difference equation using the analytic data to fit DBH had good goodness of fit. 2） using the Korf basic equation and Korf difference equation， the single form site index table and the polymorphic site index table of Chinese fir plantation in Hubei province was compiled by using the guide curve method， taking 20 a as the standard age and 2 cm as the exponential level. 3） both the established model and the site index table passed the test， and the test accuracy of the difference equation was 99.61%， higher than 96.97% of the basic equation. The polymorphic site index table was 1.18% higher than single form site index table. It can be seen that， the index table of DBH site of Chinese fir plantation in Hubei province compiled by difference equation is more accurate than the basic equation and can evaluate the site quality of Chinese fir plantation in Hubei province more accurately.

Keywords：Chinese fir plantation; single form site index table; polymorphic site index table; DBH growth equation; difference equation; guide curve

收稿日期：2022-07-04

基金项目：湖北省林业科技支撑项目 （2022LYKJ03）

第一作者简介：马羽，硕士研究生。研究方向为森林生态学。Email： 1461157447@QQ.com

*通信作者：邓湘雯， 博士，教授，博士生导师。研究方向为森林生态学。Email： dxwfree@126.com;许业洲， 二级研究员。研究方向为森林培育。Email： xyz0271@sina.com

引文格式：马羽， 许业洲， 袁慧， 等. 湖北省杉木人工林胸径差分方程及多形地位指数表研究[J]. 森林工程， 2023，39（2）：72-81.

MA Y， XU Y Z， YUAN H， et al. Study on DBH difference equation and polymorphic site index table of Chinese fir plantation in Hubei Province[J]. Forest Engineering， 2023，39（2）：72-81.

0引言

森林生产实践中，立地质量代表着某一立地条件下森林或某一树种的生产力[1-2]。立地质量是森林树种选择、林地更新、生产力评估和经营管理等林业工作和研究的基础[3]。且立地质量评价是研究森林的生产经营、预估林地生产力和很多森林经营活动的一个重要手段[4-6]。近些年来，关于立地质量评价方法日益成熟，形成了多种立地质量的评价方法[7-9]，其中地位级法和地位指数法最为常见[10-11]。地位指数表是森林经营工作、立地质量评价的基础数表，近些年，使用地位指数表对立地质量进行评价在国内外十分广泛[12-18]。

在评价森林的立地质量时，林分结构常常影响立地质量的评价结果，且树种不同影响大小也不同[19]。在国内外学者的研究中，评估林分立地质量多采用以林分优势木平均高为指标的地位指数法[3，20]，李斌成等[21]以解析木（优势木）树高数据，采用导向曲线法和差分方程法编制了湖北省杉木立地指数表；段爱国等[22]通过杉木（优势木）的解析木数据，以年龄-树高为材料，编制了多种多形地位指数方程。

相比较而言，虽然以树高为指标编制的地位指数表受密度等因素影响较小，但因树高受林分状况以及测量方法等因素的影响，测量困难且精度不高；而胸径作为森林资源调查中和树高同样重要的测树因子，杉木的胸径生长与其树高一样均符合速生针叶树种的生长规律，且胸径较树高测定简单、准确[23-24]。因此在没有或者不考虑林分密度效应时，胸径可以代替树高来评价立地质量。目前国内以胸径为指标，编制地位指数表较少。马炜等[25]通过二类清查数据，采用数式法编制了长白落叶松胸径地位级表，检验结果表明，所编制的胸径地位级表，不但能直接用于立地质量评价，也可预测不同立地条件下林木胸径生长；刘洵等[3]以湖南省国家森林资源连续清查数据利用标准差调整法、变动系数调整法以及相对胸径法分别编制湖南栎类天然次生林胸径地位指数表，检验结果表明3种方法编制的胸径地位指数表均具有较高精度；唐增银等[26]以平均优势木胸径数据，编制了鲁北地區泡桐的立地等级表，具有较强的适用性；李振芳等[27]编制了湖北省泡桐人工林胸径地位级表，其精度高，对湖北泡桐人工林可以进行客观地评价；龚召松等[28]编制了楠木次生林胸径地位指数表，经检验，所编制的地位指数表可以稳定地反映湖南省楠木次生林的立地质量。以上研究表明，应用胸径作为指标也可以很好地反映树木的生长特性，对林地的立地质量做出准确的评估，并且不需测量树高，降低了外业难度的同时，使测得的胸径较树高更加精确。故用胸径作为指标编制地位指数表是极为合理且可行的。

杉木（Cunninghamia lanceolata）是我国特有的针叶用材树种，是南方各省区重要的造林树种，至今已有1 600多年的种植历史[29-31]。截至2019年第九次全国森林资源清查结果显示，目前全国杉木人工林造林总面积为9.90×106 hm2，占全国造林总面积的27.23%；蓄积量达7.55×108 m3，占全国总蓄积量的32.57%，均排名第一，在全国的商品用材树种中有举足轻重的作用[29，32]。杉木分布广泛，在我国亚热带山地、热带北缘和暖温带南缘等气候区的多个省区均有大量种植。湖北省处于国内杉木产区的北缘地带，杉木栽种历史悠久，杉木作为湖北省的优势树种，分布于湖北省的西部及东南部，其覆盖面积约占湖北省丰产林总面积的40%[33]。

湖北省的杉木研究一直以来以良种选育和栽培为主[33-34]，在良种选育和栽培方面取得了相当大的成就，而以往的杉木人工林的立地质量评价已不能适应新变化的需求，因此，对杉木人工林生长与立地质量评价进行系统研究，是湖北省杉木人工林及其产业发展较为紧迫的基础性工作。故本研究以湖北省全省杉木人工林为研究对象，采用平均木的解析木数据，对导向曲线进行拟合，并分别建立全省杉木人工林单形地位指数表和多形地位指数表，为湖北省杉木人工林立地质量评价与合理经营提供参考。

1研究区概况

湖北省地处中国中部地区，位于长江中游，地处29°01′53″～ 33°06′47″N，108°21′42″～ 116°07′50″E，以山地丘陵为主要地貌，地势为西、北、东三面环山，西高东低，中间低平，略呈向南敞开的不完整盆地，属于中国东南低山丘陵向西南高山高原的过渡带。在全省总面积中，山地占56%，丘陵占24%，平原湖区占20%。全省除高山地区外，大部分属亚热带季风性湿润气候，年平均气温16 ℃，无霜期230～ 300 d，年平均降水量800～1 600 mm，降雪总时间为11～ 12 d，气候湿润，雨热同季。全省林木种质资源丰富，森林类型多样，其中杉木主要在低山丘陵地带种植，主要栽培区在鄂南幕阜山系、鄂西南巫山山系和鄂东大别山山系等，是我国南方重点林区之一[21，25，27]。

2研究方法

2.1数据来源

以全省杉木人工林为对象，采用湖北省杉木人工林解析木（平均木）数据，解析木数据取自2016—2017年在湖北省鄂东南、鄂西南、鄂西北地区的共94块样地，样地面积20 m×30 m，每块样地进行每木检尺，测量的指标包括树高、胸径、冠幅和活枝下高等，并记录地理位置、立地环境、造林年度和造林密度等信息。每块样地选择3株平均木进行树干解析，并拟合解析木的皮厚，计算带皮直径。剔除数据录入不全的数据，按3倍标准差法（胸径平均值±3倍标准差）剔除异常值[7，27]，最终得到282株解析木数据及其5 849个圆盘数据。最后按模型拟合数据与检验数据比例为8∶2的原则[4，7]，随机留取58株解析木的1 184个圆盘数据作为曲线模型和地位指数表的验证数据，其余数据作为拟合方程与编表数据来源。数据详细信息见表1。

2.2导向曲线的选择

2.2.1基础生长方程

杉木胸径随林龄的生长规律近似“S”形的生长曲线，故本研究选择了7种常见的数学模型，见表2，表2中D为胸径；t为林龄；a、b、c为模型参数。整理解析木数据，用R4.04软件分别对方程进行拟合处理，最后进行检验[21]。

2.2.2差分方程

当数据为长期观测资料或解析木资料时，采用差分方程更为适宜[36]。参考段爱国等[22]的相关研究，对理查德、逻辑斯蒂和考尔夫等理论方程进行差分运算，通过差分消元法，得到不同的差分方程，见表3，表3中D1、D2为胸径；t1、t2为林龄；a、b、c为模型参数。对解析木数据进行整理，得到双胸径-双年龄数据，并运用R 4.0.4软件进行差分方程的拟合[22]。

2.2.3曲线拟合优度的评价

为了比较各模型的拟合效果，误差均方根（RMSE，公式中用RMSE表示）以及决定系数（R2）等统计指标来评估模型的拟合质量。选择误差均方根（RMSE）小、决定系数（R2）更接近1且具有生物学意义的模型为导向曲线方程。统计指标及其计算公式见表4[22]。其中obs，i、est，i、n分别表示第i个观测值，第i个估计值，观测值数目。

2.3地位指數表的编制

2.3.1标准年龄和指数级的确定

确定标准年龄的目的是寻找胸径生长趋于稳定且能灵敏反映立地差异的年龄[7]。计算标准年龄的方法是先确定杉木胸径的变动系数，当杉木胸径变动系数趋于稳定时，即认为此林龄为标准年龄。

RMSE=∑ni=1（obs，i-est，i）2n

（13）

决定系数

Coefficient of

determination

R2

R2=1-∑ni=1（obs，i-est，i）2∑ni=1（obs，i-e-st，i）2

（14）

杉木胸径的变动系数公式如下

CD=SAiDi。 （15）

式中：CD为胸径的变动系数；SAi为各龄级胸径的标准差；Di为各龄级理论胸径值。

指数级距是根据杉木在标准年龄时的胸径变动幅度，再基于树种的生长特性确定的。一般的指数级距是1～4 cm，分为10个[7]。本研究根据标准年龄时杉木胸径的变动幅度相应划为若干立地指数级。

2.3.2单形地位指数表

比较选择最优的方程为导向曲线模型，拟合各龄阶的理论胸径值，计算各龄级的调整系数（Kj）

Kj=DOjDOk×100%。 （16）

式中：Kj为调整系数；DOj为地位指数级；DOk为基准年龄时胸径理论值。

再求得各龄阶指数级胸径（Dij）

Dij=Kj×Dik 。 （17）

式中，Dik为各龄阶胸径理论值。

2.3.3多形地位指数表

选择表4中较优的差分方程，设D=D2，t=t1，SI=D1，T=t1，其中SI、T分别表示地位指数和指数年龄，t为龄阶、D为理论胸径，将各变量代入差分方程求出各龄阶胸径即为多形地位指数表[22]。

2.4模型、地位指数表的检验

利用未参加建模的数据，对导向曲线及地位指数表进行精度检验。检验指标包括平均相对误差（R-）、相对总误差（Q）、相对误差限（E）、精度（P），具体计算公式参考文献 [27]。

落点检验：将待检验的58株解析木的1 184个圆盘数据作散点图，绘制到地位指数曲线簇图上，算出散点落在曲线簇内的概率，即为地位指数表能够解释林分平均胸径生长的概率值。

3结果与分析

3.1生长模型的拟合与比较

3.1.1基础生长方程拟合结果

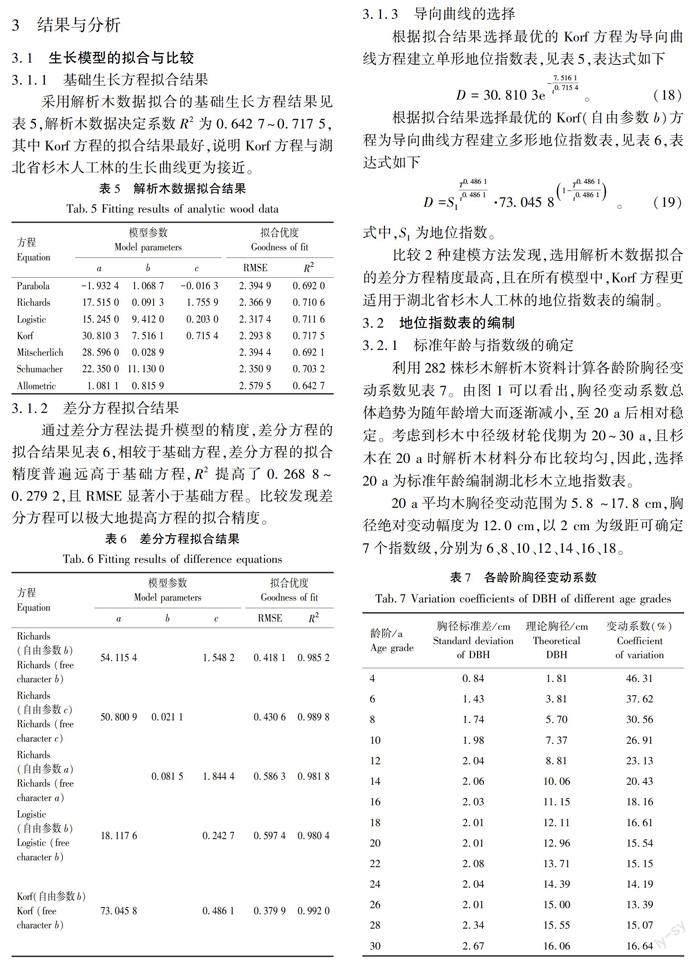
采用解析木数据拟合的基础生长方程结果见表5，解析木数据决定系数R2为0.642 7～0.717 5，其中Korf方程的拟合结果最好，说明Korf方程与湖北省杉木人工林的生长曲线更为接近。

3.1.3导向曲线的选择

根据拟合结果选择最优的Korf方程为导向曲线方程建立单形地位指数表，见表5，表达式如下

D=30.810 3e-7.516 1t0.715 4。 （18）

根据拟合结果选择最优的Korf（自由参数b）方程为导向曲线方程建立多形地位指数表，见表6，表达式如下

D=SIT0.486 1t0.486 1·73.045 81-T0.486 1t0.486 1。 （19）

式中，SI为地位指数。

比较2种建模方法发现，选用解析木数据拟合的差分方程精度最高，且在所有模型中，Korf方程更适用于湖北省杉木人工林的地位指数表的编制。

3.2地位指数表的编制

3.2.1标准年龄与指数级的确定

利用282株杉木解析木资料计算各龄阶胸径变动系数见表7。由图1可以看出，胸径变动系数总体趋势为随年龄增大而逐渐减小，至20 a后相对稳定。考虑到杉木中径级材轮伐期为20～30 a，且杉木在20 a时解析木材料分布比较均匀，因此，选择20 a为标准年龄编制湖北杉木立地指数表。

20 a平均木胸径变动范围为5.8 ～17.8 cm，胸径绝对变动幅度为12.0 cm，以2 cm为级距可确定7个指数级，分别为6、8、10、12、14、16、18。

3.2.2单形地位指数表的编制

根据式（18），计算各龄阶胸径的理论值，再求得各指数级调整系数Kj，编制湖北省杉木人工林单形地位指数表，见表8。

3.2.3多形地位指数表的编制

选择Korf方程（自由参数b）为导向曲线，采用表达式（19）计算，其中标准年龄T=20 a，将地位指数SI和林龄t代入式中，求得各龄阶指数级胸径，将其整理得到湖北省杉木人工林多形地位指数表，见表9。

3.3模型及数表检验

3.3.1导向曲线的检验

对基础方程与差分方程进行精度检验，检验结果见表10，基础方程的相对误差限为3.02%，精度为96.97%；差分方程的相对误差限为0.38%，精度为99.61%。基础方程与差分方程拟合的胸径理论值与真实值的偏差均小于5%，模型的实用性较好，估计精度可靠。且差分方程拟合的精度较基础方程更高，说明差分方程能更准确地预估湖北省杉木人工林的生长。

3.3.2地位指数表的检验

对得到的单形立地曲线簇和多形立地曲线簇进行落点检验，将用于检验的58株解析木共1 184个圆盘数据分别绘制到胸径单形地位级曲线簇和多形地位级曲线簇上。由图2和图3可知，大部分解析木圆盘数据都落在曲线簇内，仅有86个圆盘数据落在单形地位指数表的曲线簇外，落点精度92.74%；仅有72个圆盘数据落在多形地位指数表的曲线簇外，落点精度93.92%。检验结果表明，所编单形地位指数表及多形地位指数表均可以解释大部分杉木人工林胸径生长情况，2个地位指数表均通过检验，且多形地位指数表较单形地位指数表的检验精度高出1.18%，说明杉木人工林多形地位指数表具有更高的预估精度，更能准确地评价湖北省杉木人工林的生长情况。

4结论与讨论

1）利用湖北省各地共282株杉木人工林解析木（平均木）数据，对杉木不同龄阶林分平均胸径数据进行分析处理，并选择Korf方程（18）作为湖北杉木人工林胸径单形地位指数表的导向曲线；式（19）为多形地位指数表的导向曲线，分别编制湖北省杉木人工林的单形胸径地位指数表与多形地位指数表，经检验均可用于湖北省杉木人工林的立地质量评价。模型的拟合结果表明，差分方程的拟合结果较基础方程更好，这与段爱国等[22]研究得出的差分方程拟合精度高、表现更优的研究结论相同。在基础方程的选择与差分方程的选择中，Korf方程均比其他方程的拟合精度更高，这与李斌成等[21]及段爱国等[22]的研究结果相似；从差分方程的拟合结果来看，以b或c为自由参数的拟合优度要高于以a为自由参数的拟合优度，这与相聪伟[37]的研究结果一致，再次表明以胸径为指标编制的地位指数表可以很好地评价立地质量，同时外业测量更加简单且精确。

2）本研究采用湖北省杉木人工林解析木（平均木）数据，尽管固定样地数据是最理想的建模数据[38]，但实际中固定样地数据较难获取，而解析木数据有数据范围广、随机性强等特点。通过拟合结果发现，解析木数据可以代表湖北省杉木人工林的生长状况，适宜建模；经过检验，解析木数据可以很好地用来编制地位指数表，这也与郑聪慧等[39]选择的数据一致。

3）通过所编制的地位等级表，并对照全省解析木数据，可以对湖北全省的杉木人工林立地质量做出评价。将地位指数6、8 cm视为较低水平的立地等级；10、12、14 cm视为中等水平的立地等级；16、18 cm视为较高水平的立地等级，以多形地位指数表为依据，则湖北省杉木人工林有11.60%处于较低水平；69.97%处于中等水平；18.43%处于较高水平，湖北省杉木人工林大部分处于中等立地水平，基本符合湖北省杉木人工林立地质量现状，与李斌成等[21]根据优势高编制的多形地位指数表所得出的结论相似，能够为湖北省杉木人工林的立地质量评价提供基础数据和理论依据。

4）本研究將282株解析木数据以8∶2的比例分为编表数据与检验数据，这样可以避免检验样本与编表样本的耦合，并用检验数据对拟合的导向曲线进行了精度检验，对所编的单形地位指数表与多形地位指数进行落点检验，结果表明2个导向曲线与地位指数表均通过了检验，且差分方程的检验精度高于基础方程；多形地位指数表的检验精度高于单形地位指数表，这与李斌成等[21]和段爱国等[22]的研究结果相一致，相较于基础方程，差分方程拥有更高的拟合精度，能更精确地拟合大范围的数据。

【参考文献】

[1]EVERETT C J， THORP J H. Site quality evaluation of loblolly pine on the South Carolina Lower Coastal Plain， USA[J]. Journal of Forestry Research， 2008， 19（3）： 187-192.

[2]黄国胜，马炜，王雪军，等.基于一类清查数据的福建省立地质量评价技术[J].北京林业大学学报，2014，36（3）：1-8.

HUANG G S， MA W， WANG X J， et al. Forestland site quality evaluation of Fujian Province based on continuous forest inventory data[J]. Journal of Beijing Forestry University， 2014， 36（3）： 1-8.

[3]刘洵，曾思齐，龙时胜，等.湖南省栎类天然次生林胸径地位指数表研制[J].森林与环境学报，2019，39（3）：265-272.

LIU X， ZENG S Q， LONG S S， et al. Establishment of a diameter at breast height site index table for natural secondary oak forest in Hunan Province[J]. Journal of Forest and Environment， 2019， 39（3）： 265-272.

[4]吴恒，党坤良，田相林，等.秦岭林区天然次生林与人工林立地质量评价[J].林业科学，2015，51（4）：78-88.

WU H， DANG K L， TIAN X L， et al. Evaluating site quality for secondary forests and plantation in Qinling Mountains[J]. Scientia Silvae Sinicae， 2015， 51（4）： 78-88.

[5]韩培新.韶关市尾巨桉、巨尾桉短周期工业原料林地位指数表的编制[J].林业调查规划，2012，37（4）：1-4，8.

HAN P X. Site index table compilation for short-rotation industrial raw material forest of Eucalyptus grandis and Eucalyptus urophy plantation in Shaoguan[J]. Forest Inventory and Planning， 2012， 37（4）： 1-4， 8.

[6]曹元帅，孙玉军.基于广义代数差分法的杉木人工林地位指数模型[J].南京林业大学学报（自然科学版），2017，41（5）：79-84.

CAO Y S， SUN Y J. Generalized algebraic difference site index model for Chinese fir plantation[J]. Journal of Nanjing Forestry University （Natural Sciences Edition）， 2017， 41（5）： 79-84.

[7]孟宪宇.测树学[M].3版.北京：中国林业出版社，2006：107-108.

MENG X Y. Dendrology[M]. 3rd ed. Beijing： China Forestry Publishing House， 2006：107-108.

[8]唐诚.西南桦人工林生长模拟及立地质量评价[D].北京：中国林业科学研究院，2017.

TANG C. Growth modeling and site quality evalution for Betula alnoides plantations[D]. Beijing： Chinese Academy of Forestry， 2017.

[9]CIESZEWSKI C J. Three methods of deriving advanced dynamic site equations demonstrated on inland Douglas-fir site curves[J]. Canadian Journal of Forest Research， 2001， 31（1）： 165-173.

[10]翟文元，许玉婷，夏泰英，等.山东省107-杨树地位指数表的编制[J].山东农业大学学报（自然科学版），2012，43（2）：227-231.

ZHAI W Y， XU Y T， XIA T Y， et al. Development of site index table of 107-poplar[J]. Journal of Shandong Agricultural University （Natural Science Edition）， 2012， 43（2）： 227-231.

[11]羅也，杨雨春，王君，等.吉林省长白山区胡桃楸天然次生混交林立地指数模型[J].应用生态学报，2019，30（12）：4049-4058.

LUO Y， YANG Y C， WANG J， et al. Site index model of Juglans mandshurica natural secondary mixed forest in Changbai Mountain area， Jilin Province， China[J]. Chinese Journal of Applied Ecology， 2019， 30（12）： 4049-4058.

[12]杨传强，李士美，孔雨光，等.山东省松类人工林立地指数表的编制与应用[J].林业资源管理，2018（2）：43-47，118.

YANG C Q， LI S M， KONG Y G， et al. Establishment and application of site index table for Pinus spp. in Shandong Province[J]. Forest Resources Management， 2018（2）： 43-47， 118.

[13]孟宪宇，陈东来.山杨次生林地位指数表编制方法的研究[J].北京林业大学学报，2001，23（3）：47-51.

MENG X Y， CHEN D L. Study on constructive method of site index table for poplar secondary forest[J]. Journal of Beijing Forestry University， 2001， 23（3）： 47-51.

[14]MATHIASEN R L， OLSEN W K， EDMINSTER C B. Site index curves for white fir in the southwestern United States developed using a guide curve method[J]. Western Journal of Applied Forestry， 2006， 21（2）： 87-93.

[15]马丰丰，贾黎明，段劫，等.北京山区侧柏人工林立地指数表的编制[J].北京林业大学学报，2008，30（6）：78-82.

MA F F， JIA L M， DUAN J， et al. Compilation of site index table for plantations of Platycladus orientalis in Beijing mountainous area[J]. Journal of Beijing Forestry University， 2008， 30（6）： 78-82.

[16]潘国兴，张忠远.安徽亳县泡桐立地质量评定[J].林业科学，1991，27（2）：102-110.

PAN G X， ZHANG Z Y. Evaluation on the site quality of paulownia in Bo County Anhui[J]. Scientia Silvae Sinicae， 1991， 27（2）： 102-110.

[17]CIESZEWSKI C J， STRUB M. Generalized algebraic difference approach derivation of dynamic site equations with polymorphism and variable asymptotes from exponential and logarithmic functions[J]. Forest Science， 2008， 54（3）： 303-315.

[18]CIESZEWSKI C J. Comparing fixed- and variable-base-age site equations having single versus multiple asymptotes[J]. Forest Science， 2002， 48（1）： 7-23.

[19]MACFARLANE D W， GREEN E J， BURKHART H E. Population density influences assessment and application of site index[J]. Canadian Journal of Forest Research， 2000， 30（9）： 1472-1475.

[20]王艷辉，曾思齐，王伟，等.马尾松次生林地位指数表的编制[J].内蒙古林业科技，2007，33（3）：17-20.

WANG Y H， ZENG S Q， WANG W， et al. Establishment of site index table for Pinus massoniana secondary forests[J]. Inner Mongolia Forestry Science and Technology， 2007， 33（3）： 17-20.

[21]李斌成，杜超群，袁慧，等.基于理论模型及其差分方程的湖北省杉木立地指数表研制[J].中南林业科技大学学报，2019，39（7）：56-64.

LI B C， DU C Q， YUAN H， et al. Development of site index table of Chinese fir in Hubei Province based on theoretical model and difference equation[J]. Journal of Central South University of Forestry & Technology， 2019， 39（7）： 56-64.

[22]段爱国，张建国.杉木人工林优势高生长模拟及多形地位指数方程[J].林业科学，2004，40（6）：13-19.

DUAN A G， ZHANG J G. Modeling of dominant height growth and building of polymorphic site index equations of Chinese fir plantation[J]. Scientia Silvae Sinicae， 2004， 40（6）： 13-19.

[23]SHARMA M， PARTON J. Height–diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach[J]. Forest Ecology and Management， 2007， 249（3）： 187-198.

[24]李海奎，法蕾.基于分级的全国主要树种树高-胸径曲线模型[J].林业科学，2011，47（10）：83-90.

LI H K， FA L. Height-diameter model for major tree species in China using the classified height method[J]. Scientia Silvae Sinicae， 2011， 47（10）： 83-90.

[25]马炜，孙玉军.长白落叶松人工林立地指数表和胸径地位级表的编制[J].东北林业大学学报，2013，41（12）：21-25，38.

MA W， SUN Y J. Compilation of site index table and site class table for Larix olgensis plantations[J]. Journal of Northeast Forestry University， 2013， 41（12）： 21-25， 38.

[26]唐增银，李本和.鲁北泡桐立地等级评定[J].山东林业科技，1991，21（S1）：36-42.

TANG Z Y， LI B H. Site grade evaluation of paulownia in northern Shandong Province[J]. Journal of Shandong Forestry Science and Technology， 1991， 21（S1）： 36-42.

[27]李振芳，许业洲，唐万鹏，等.湖北省泡桐人工林胸径地位级表的编制[J].东北林业大学学报，2016，44（9）：14-19，23.

LI Z F， XU Y Z， TANG W P， et al. Establishing site class table for paulownia plantation in Hubei[J]. Journal of Northeast Forestry University， 2016， 44（9）： 14-19， 23.

[28]龚召松，曾思齐，贺东北，等.湖南楠木次生林胸径地位指数表的研制[J].中南林业科技大学学报，2019，39（7）：48-55.

GONG Z S， ZENG S Q， HE D B， et al. Establishment of DBH site index table for Phoebe zhennan secondary stand in Hunan[J]. Journal of Central South University of Forestry & Technology， 2019， 39（7）： 48-55.

[29]袁慧，杜超群，李斌成，等.湖北省杉木生长模型研究[J].中国农学通报，2019，35（34）：50-58.

YUAN H， DU C Q， LI B C， et al. The growth model of Cunninghamia lanceolata in Hubei[J]. Chinese Agricultural Science Bulletin， 2019， 35（34）： 50-58.

[30]吴中伦.杉木[M].北京：中国林业出版社，1984.

WU Z L. Fir wood[M]. Beijing： China Forestry Publishing House， 1984.

[31]任正標，郭传阳，郑鸣鸣，等.间伐对杉木凋落物分解中生态化学计量的影响[J].西部林业科学，2021，50（2）：109-115，123.

REN Z B， GUO C Y， ZHENG M M， et al. Effect of thinning intensity on ecological stoichiometry in litters decomposition of Cunninghamia lanceolata[J]. Journal of West China Forestry Science， 2021， 50（2）： 109-115， 123.

[32]鲁乐乐，王震，张雄清，等.基于贝叶斯模型平均法和逐步回归法构建杉木单木胸径生长模型[J].林业科学，2021，57（9）：87-97.

LU L L， WANG Z， ZHANG X Q， et al. Individual tree diameter growth model of Chinese fir plantations using Bayesian model averaging and stepwise regression approaches[J]. Scientia Silvae Sinicae， 2021， 57（9）： 87-97.

[33]许业洲.湖北省林木育种工作的现状与建议[J].湖北林业科技，2016，45（4）：6-8，62.

XU Y Z. The current situation and suggestion of the forest tree breeding in Hubei Province[J]. Hubei Forestry Science and Technology， 2016， 45（4）： 6-8， 62.

[34]庞宏东，王晓荣，张家来，等.湖北省不同森林类型和不同地区间林下灌木层生物量和碳密度特征[J].西北林学院学报，2014，29（6）：46-51.

PANG H D， WANG X R， ZHANG J L， et al. Characteristics of shrub layer biomass and carbon density in different forest types and different regions in Hubei Province[J]. Journal of Northwest Forestry University， 2014， 29（6）： 46-51.

[35]許业洲，王起富，余义，等.杉木短周期小径材培育模式的林分直径结构及经营要素预测[J].东北林业大学学报，2021，49（2）：18-23，30.

XU Y Z， WANG Q F， YU Y， et al. Stand diameter structure and management factor prediction of Chinese fir short-cycle cultivation model[J]. Journal of Northeast Forestry University， 2021， 49（2）： 18-23， 30.

[36]AMARO A， REED D， TOME M， et al. Modeling dominant height growth： Eucalyptus plantations in Portugal[J]. Forest Science， 1998， 44（1）： 37-46.

[37]相聪伟.杉木人工林立地指数方程的研究[D].北京：中国林业科学研究院，2010.

XIANG C W. Study on site index equation of Cunninghamia lanceolata plantations[D]. Beijing： Chinese Academy of Forestry， 2010.

[38]RAULIER F， LAMBERT M C， POTHIER D， et al. Impact of dominant tree dynamics on site index curves[J]. Forest Ecology and Management， 2003， 184（1/2/3）： 65-78.

[39]郑聪慧，贾黎明，段劼，等.华北地区栓皮栎天然次生林地位指数表的编制[J].林业科学，2013，49（2）：79-85.

ZHENG C H， JIA L M， DUAN J， et al. Establishment of site index table for Quercus variabilis natural secondary forest in North China[J]. Scientia Silvae Sinicae， 2013， 49（2）： 79-85.