“鸡兔同笼总复习”教学设计

李雪贞

教学内容：

数学人教版四年级下册第106～107页及相关内容。

学习目标：

1.进一步了解“鸡兔同笼”问题，经历解决“鸡兔同笼”问题的过程，培养逻辑推理能力，体会假设思想。

2.通过练习，能熟练应用列表猜测、假设等方法解决“鸡兔同笼”问题，掌握解决问题的基本策略，建立解决这类问题的模型，提高分析问题和解决问题的能力，培养推理意识。

3.在练习过程中，感受数学的价值，提高学习数学的兴趣。增强应用意识和实踐能力。

学习重点：

加深对“鸡兔同笼”问题的认识，灵活应用知识解决生活中的“鸡兔同笼”问题。

学习难点：

提高分析问题和解决问题的能力。

教学过程：

一、导学生疑，引出问题

出示狗熊岭植树视频，问：植树节中会有什么样的数学问题呢？请同学们猜一猜。（鸡兔同笼问题）今天我们就一起来复习“鸡兔同笼”问题。（板书课题：鸡兔同笼总复习）那你们还记得我们解决这类问题的方法吗？（列表猜测法、画图法、假设法）每一种题型三种方法都适用吗？

生：不是。列表猜测法和画图法适用于数字比较小的题目中，而数字比较大的时候，用假设法比较合适。

师：同学们真厉害！那你们能不能灵活应用这些方法来解决“鸡兔同笼”问题呢？

设计意图：莎士比亚说：“学问必须合乎自己的兴趣，方可得益。”以学生喜欢的动画片植树视频导入，既能激起学生的学习兴趣，又能增强学生的环保意识。猜一猜能培养学生发现问题的能力。

二、多样学法，理解问题

（一）自学基础

狗熊岭中的植树节会有什么样的“鸡兔同笼”问题呢？我们一起来看一看。

出示题目：植树节到了，狗熊岭全员开始植树。8名队员一共植了30棵树。光头强队每名队员植3棵，熊大队每名队员植4棵。光头强队有几名队员？熊大队有几名队员？

1.自主读题目，找出已知条件、所求问题。

2.找出题目中什么相当于鸡？什么相当于兔？什么相当于总头数？什么相当于总脚数？（光头强队的一名队员相当于鸡，熊大队的一名队员相当于兔，8名队员相当于总头数，30棵树相当于总脚数。）

3.先猜一猜，用不同的方法独立解答。

4.抽学生交流，全班订正。

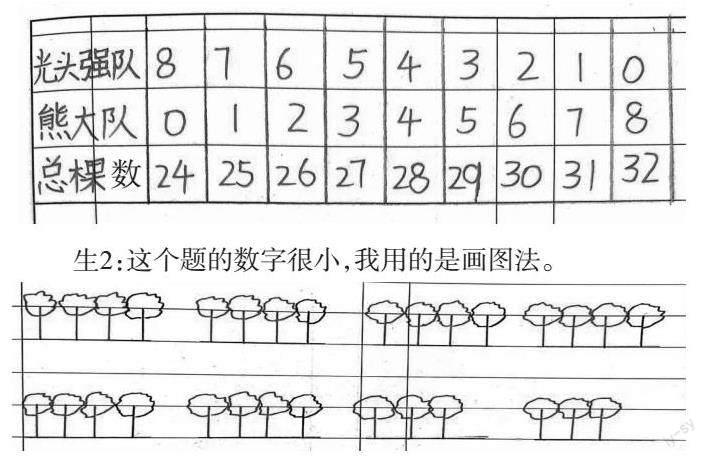
预设：生1：这个题的数字不是很大，我用的是列表法。

生2：这个题的数字很小，我用的是画图法。

生3：我用的是假设法。

假设8名队员都是光头强队的。

植树棵树：8×3=24（棵），这样就比实际少了：30-24=6（棵），光头强队每名队员植树的棵树比熊大队每名队员植树的棵树少：4-3=1（棵），少的6棵树里有几个1棵，熊大队就有几名队员。

熊大队的队员数：6÷1=6（名）；

光头强队的队员数：8-6=2（名）。

检验：熊大队植树的棵树加光头强队植树的棵树是否等于30棵。

6×4+2×3

=24+6

=30（棵）

解答正确。

答：光头强队有2名队员，熊大队有6名队员。

设计意图：复习课也不能忽视基础知识和基本技能的有效掌握。虽然已经有上一节的学习基础，但对于一大部分学生来说，理解不够透彻，学得还不够扎实，从数字小的简单的题目入手，鼓励学生采用不同的解题方法，体现了解决问题策略的多样性。列表猜测法、画图法帮助理解算理，进一步建立解决“鸡兔同笼”问题的数学模型。

（二）互学典型

小强有1角的硬币和5角的硬币共40枚，总面值为10元。两种硬币各有多少枚？

1.自主读题目，找出已知条件、所求问题。

2.找出题目中什么相当于鸡？什么相当于兔？什么相当于总头数？什么相当于总脚数？（1角的硬币相当于鸡，5角的硬币相当于兔，40枚硬币相当于总头数，10元相当于总脚数。）

3.观察比较：这题和上一题有什么不同，采用什么方法比较合适？

4.引导学生发现：（1）这题的单位不相同，需要先化单位；（2）数字比较大，采用假设法比较合适。

5.自己独立解答，解答有困难的同学可以请小组内的同学帮忙，并在小组内交流自己的做法。

6.抽一个同学交流，全班订正。

10元=100角

假设全是面值1角的硬币

1×40=40（角）

100-40=60（角）

5-1=4（角）

5角硬币的枚数：60÷4=15（枚）

1角硬币的枚数：40-14=25（枚）

检验：15×5+25×1

=75+25

=100（角）=10（元）

解答正确。

答：5角的硬币有15枚，1角的硬币有25枚。

设计意图：深入建立“鸡兔同笼”问题的数学模型，让学生感受到假设法的优越性，体现推理意识的核心素养。

（三）展学易错

阳光小学举办数学竞赛，共有20道题，每做对一道得5分，不做或做错一道扣2分。王亮共得79分，他做对了几道题？

1.自主读题目，找出已知条件、所求问题。

2.自己尝试解答，并和同桌交流做法。

3.抽两位同学到黑板上板演。（做错的和做对的）

预设：生1：假设20道题全部做错。

20×2=40（分），79-40=39（分），5-2=3（分）。

做对的道数：39÷3=13（道）

做错的道数：20-13=7（道）

检验：13×5+7×2

=65+14

=79（分）

答：他做对了13道。

生2：假设20道题全做对。

20×5=100（分），100-79=21（分），5+2=7（分）。

做错的道数：21÷7=3（道）；

做对的道数：20-3=17（道）。

检验：17×5-3×2

=85-6

=79（分）

答：他做对了17道。

4.引导学生观察：两个同学的解答，你有什么发现？

（两位同学的检验结果都是79分，而两位同学的答对道数和答错道数却是不相同的。）那你们觉得这个题会有两个答案吗？（不会）谁有什么要提醒的？（我要提醒：得5分和扣2分相差的是7分）

5.易错提醒：解决此题的关键做对一道得5分和不做或做错一道扣2分相差的分数不是5-2=3（分），而是5+2=7（分）；求做对几道题，不是假设全部做错，而是要假设全部做对，先求出做错的道数，再求出做对的道数。

设计意图：课堂因出错而精彩。这个环节，我一开始没有领着学生一起找易错点，目的就是要让学生出错，抓住课堂中出错资源，并加以利用，这样学生才会理解得更深刻。

三、練学提升，巩固问题

1.小强有三角形、长方形的卡片共40张，这些卡片共有145个角，两种卡片各有多少张？

2.（出示中国女篮晋级世界杯四强决赛视频）2022年9月29日，中国女篮以总分85：71战胜法国队，再次晋级世界杯四强。总得分包括三分球得分、二分球的得分和其他得分。其中中国队的其他得分为7分，那中国队进了几个三分球和进了几个二分球？

3.思维拓展

100个和尚吃100个馒头。大和尚一人吃3个，小和尚3人吃一个。求大、小和尚各多少人？

设计意图：三个练习题的设计层层递进，让学生的思维发展得到进阶。数学复习课本来就很枯燥，观看中国女篮晋级世界杯四强决赛视频，不仅能让学生感受到运动员们顽强拼搏的精神，进而激起学生对难题的挑战动力；而且还能开阔学生的视野，激发学生的民族自豪感和爱国情感。

四、拓展延伸，内化问题

1.通过这节课的学习你有什么收获？

2.通过学习，我们感受到了“鸡兔同笼”问题无处不在。在我们周围也有许多“鸡兔同笼”问题，请同学们留心观察、认真思考，创造出至少一题“鸡兔同笼”的数学问题，并独立解答。

设计意图：创新是一个民族的灵魂。《义务教育数学课程标准（2022年版）》进一步将“创新意识”作为核心素养在义务教育阶段的主要表现之一，以及对整个义务教育阶段提出的跨学科的要求。教学要与学生的生活经验相结合，让学生在生活中发现问题、提出问题、分析问题、解决问题。感受数学的魅力，并内化“鸡兔同笼”问题的解题方法。