关注学生本真，构建有效复习课堂

赵会

“平面图形面积的整理复习”是六年级下册的一节关于小学阶段平面图形面积的系统复习课。平面图形的面积计算公式的推导过程是分册、分散教学的，针对学生已经拥有的碎片化知识，教师必须立足于学生的学情，选择能引发学生积极参与、独立思考的教学方式，引导学生自主梳理知识、查漏补缺、纠正错误，在交流、反思中理清知识脉络，构建知识网络，提高学生的思维能力，构建有效复习课堂。

片段一：一个问题引领回忆，构建知识网络

师：老师带来了一个信封，这个信封里装着一个平面图形，它的面积可以用“6.28×2”来计算，请你猜猜它可能是什么图形？为什么？

生1：有可能是长方形，因为长方形的面积=长×宽，这个6.28可能是长，2可能是宽。

师：把“长方形的面积=长×宽”贴在黑板上。

生2：有可能是平行四边形，因为平行四边形的面积=底×高，这个6.28可能是底，2可能是高。

师：把“平行四边形的面积=底×高”贴在黑板上。

生3：有可能是圆形，因为圆形的面积=3.14×半径×半径，假设它的半径是2，那么列式是：3.14×2×2，所以6.28是3.14×2的积。

这时学生会沉默不语

师：你们为什么不猜它是正方形的呢？

生4：不可能，因为正方形的面积=边长×边长，两个数字是一样的，而6.28和2不相同。

师：你们为什么不猜它是三角形的呢？

生5：不可能是三角形，因为三角形的面积=底×高÷2，

师：如果有个三角形的面积就与“6.28×2”的计结果相等，那这个三角形会是什么样的？请同学们想一想，讨论一下。

（生议论纷纷，不一会儿孩子们陆续举手了）

生6：有可能是三角形，三角形的底可能是12.56，高是2，可以先用12.56÷2=6.28，再乘高2。

生7：有可能是三角形，三角形的底是2，高是12.56，它先用12.56÷2=6.28，再乘底2。

（全场响起了掌声）

师：太棒了！（出示PPT演示对比验证）

师：除了这些以外有没有猜它是梯形的？

生：有了刚才三角形的经历，打开了学生的思维，这会儿好多同学跃跃欲试举起了手！

生7：有可能是梯形，梯形的（上底＋下底）的和是12.56，高是2，它先用12.56÷2=6.28，再乘高2。

（全场响起了掌声）

师：是什么图形呢？现在要解开谜底了，漏出一个半圆…

生：全班异口同声：是个圆形。

师：真的吗？静思5秒钟。

生：孩子们陆续举起手，说它可能是一个不规则的几何图形。它的一端凸出来一个半圆，另一端凹进去一个与凸出的半圆完全相同的半圆，这样我们只要把凸出的半圆剪下来补到另一端就是一个规则的长方形，这个不规则的图形通过割补的方法，可以转化成一个长是6.28，宽是2的长方形，可以用“6.28×2”计算它的面积。

师：把图形完全展示，揭开谜底，和孩子们想的完全相同。

（全場响起了掌声）

师：孩子们刚才从“6.28×2”中生出了那么多平面图形的面积计算公式，看一看能不能将它们摆一摆、联一联，让大家更清楚地看到这些图形的面积之间的联系呢？谁来试一试。

生：摆一摆、联一联、说一说。

师：我们通过刚才的整理，不仅回忆了每个图形的面积，还知道了它们的联系。你会用吗？

评析：教师抛出“6.28×2”可以计算一个平面图形的面积，猜猜它可能是什么图形？为什么？这个问题，从猜谜开始到揭开谜底，教师没有说更多的话，从设计问题入手，让不同层次的学生都积极参与到教学中，在猜是什么图形中，激发了学生的学习欲望，把主动权完全还给了学生，给予学生充足时间和空间，让学生根据自身已经内化的知识经验，在时而静思、时而争议的猜一猜活动中做出判断、猜测。根据“6.28×2”是两个因数相乘的积，学生很快推断出长方形和平行四边形的面积计算公式，从6.28这个数字的特征，学生也能大胆推断圆面积计算公式。当学生沉默不语时教师及时调整问题：“怎么不猜它是…？如果有个三角形的面积就和‘6.28×2的计结果相等，那这个三角形会是什么样的？”“一石激起千层浪，从正方形到梯形的猜测，充分展现出学生思考的痕迹，让思维可视化。最大限度挖掘和对接了学生已有的经验，思维不断得到激活、深化，让所有平面图形的面积计算公式清晰地在学生的自主回忆中一一生成，谜底中用“割补法”计算不规则图形面积，让知识得到了拓展，增强了学习效果。通过“能不能将它们摆一摆、联一联，让大家更清楚地看到这些图形的面积之间的联系呢？”，让学生在亲身经历、切身体会中，把各个知识点梳理、归纳、整理形成清晰的知识网络，提高了学生的学习能力。

片段二：一张学习单，引发学生自主学习

（一）你给同学推荐什么易错题？为什么？

平面图形面积的整理复习（课前学习单）

你给同学推荐什么易错题？为什么？

友情提示：

1.请在课前收集一个易错题，先独立思考完成答题，准备在小组内交流。

2.你们小组准备推荐哪道易错题？推荐的理由是？

评析：此学习单的开放设计，改变了学生学习的方式，学习单中“你给同学推荐什么易错题？为什么？”，为“学”留足了空间去搜集整理，是一个借错纠错自主反思的过程。学生要把自己的典型的易错题推荐给同学，课前要在很多个错题中选择，课前在选择易错题的活动中，学生必须主动将学习过程中半问半抄订正的错题，重新理清解决问题的思路，不断反思“提炼”方法，把内化了的知识外化出来，学生在搜集整理中丰富了知识。

（二）小组合作交流，取长补短

评析：在小组合作交流中，学生通过动脑思考、查找解决问题的途径，动口把解题思路说出来，小组同学间根据要求进行讨论，每位同学都有表达思维想法的机会，相互间互相补充完善，实现了每个人都学有所获的目标。在交流中，共同完成学习任务，彼此倾听、分享观点，主动进行深度建构，体会解决问题的合理性、灵活性。

（三）推荐哪道易错题？推荐的理由是什么？

1.第一小组推荐：

平面图形面积的整理复习（课前学习单）

你给同学推荐什么易错题？为什么？

求阴影部分面积。

生1：请你独立思考，用你喜欢的一种方法算一算、画一画，再说一说。

生2：我先给大家讲讲第一种算法——“直接算法”。因为阴影部分是一个平行四边形，它的底是8 cm，高是6 cm，所以它的面积就是8×6=48平方厘米。（你们同意吗？你们还有什么方法？）

其他学生：睁大质疑眼睛……纷纷举起了手。

生1：平行四边形是两组对边分别平行且相等的四边形。这个图形只有一组对边平行且不相等的四边形，是梯形。直接算是如下图。（还有补充吗？）

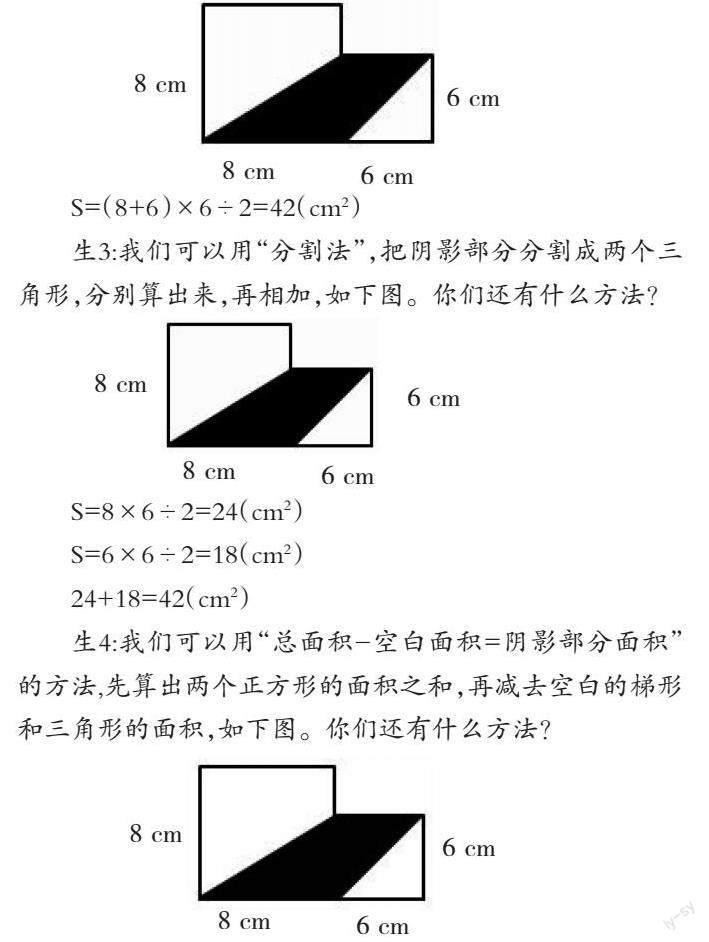
S=（8+6）×6÷2=42（cm2）

生3：我们可以用“分割法”，把阴影部分分割成两个三角形，分别算出来，再相加，如下图。你们还有什么方法？

S=8×6÷2=24（cm2）

S=6×6÷2=18（cm2）

24+18=42（cm2）

生4：我们可以用“总面积-空白面积=阴影部分面积”的方法，先算出两个正方形的面积之和，再减去空白的梯形和三角形的面积，如下图。你们还有什么方法？

S=8×8+6×6=100（cm2）

S=〔（8-6）+8〕×8÷2=40（cm2）

S=6×6÷2=18（cm2）

100-（40+18）=42（cm2）

生5：我们还可以用“添补法”，把图形的右上角再添补一下就变成一个大长方形，用长方形的面积-空白的（梯形+三角形+长方形）的面积=阴影部分面积，如下图。

S=8×8+6×6×2=112（cm2）

S=〔（8-6）+8〕×8÷2=40（cm2）

S=6×6÷2=18（cm2）

S=6×2=12（cm2）

112-（40+18+12）=42（cm2）

2.第二小组推荐：拓展训练，提高能力

你能用什么方法求下图中阴影部分面积？为什么？

（1）全体学生在作业单中独立完成。

（2）交流汇报。

生1：我用了“割补法”，把右边弓形阴影切割下来补在左边，这样整个阴影部分面积恰好是正方形面积的一半。

S=8×8÷2=32（cm2）

生2：我也用了“割补法”。把左边不规则阴影部分切割下来补在右边，这样整个阴影部分面积恰好是正方形面积的一半。

S=8×8÷2=32（cm2）

……

评析：两个小组的错题推荐抓住“你准备用什么方法求下面这个组合图形的面积？请你想一想、算一算，并说一说你的想法”这个典型，让学生经历发现问题、解决问题的全过程，站在学生的立场思考问题，引领学生主动学会审视学习内容。第一个学生用“直接算法”误认为阴影部分是一个平行四边形，教师尊重了学生个体的差异，利用了学生个体的差异，把错误当成资源，让学生在互动交流中，不断丰富自己的思考问题的方式与角度。在学生的思考、辨析中清楚地对图形的特征、计算公式的应用和多样化解题方法做了合理的解释和说明，第二小组的汇报让“割补法”和转化思想得到了升华。

总评：整节课教师只是抛出了：“（一）可能是什么图形？为什么？（二）推荐什么易错题？为什么？”这两个问题，以学生为本，充分引发学生思考、合作、表达，从而自主理清知识脉络，构建知识体系，其过程是愉悦灵动的，其收获是丰富深刻的。学生围绕问题，在议论中习得知识，整堂课教师都在“导”，学生都在“演”，必要时教师点一点以达到預设。通过推荐易错题，克服了复习课中盲目乱抓的现象，舍弃了题海战术，减轻学生负担，提高了复习补救的针对性，学生学会了如何依据错题，重点攻关、补救、反思、创新地进行复习。通过“理—联—练”的整理复习，渗透、激活所学的知识，开阔思路，培养学生的发散、创新思维能力，收到“做好一题，带活一片”的效果，从本质上构建了“平面图形面积”知识体系，进一步发展了学生的空间观念，构建了一节有效的复习课。