叶轮与导叶时序位置对井用潜水泵性能影响

刘志民，江 北，左久浩，潘 越

（河北工程大学 机械装备与工程学院，河北 邯郸 056038）

0 引言

井用多级潜水泵是一种重要的地下提水工具，广泛应用于农田灌溉、矿山工地供排水等领域[1]。它通过叶轮高速旋转，对流体做功，将流体高速抛向外围，由空间导叶收集整流高速流体，使流体的动能转换为静压能，然后逐级叠加，以此形成高扬程、高压能流体。井用多级潜水泵在运行过程中，叶轮与空间导叶之间由于动静干涉而产生压力脉动，使得泵运行的稳定性和安全性大大降低。为此，如何改善井用多级潜水泵的水力性能，减小压力脉动，提高其使用效率已成为井用多级潜水泵领域亟待解决的关键问题。

谈明高等[2]通过对节段式多级潜水泵的叶轮时序位置的研究发现，首级内压力脉动的频率、相位与幅值不受叶轮时序位置的影响，且时序角度为相邻两叶片夹角一半时，泵的整体振动水平明显降低。符恒等[3]通过改变多级轴流泵的叶轮时序位置，分析了叶轮时序位置对扬程和效率的影响规律。彭小娜等[4]研究了导叶不同时序位置下的叶片载荷分布情况，发现隔舌位于导叶两叶片之间时，可降低蜗壳不对称作用的影响，增大叶片载荷可提高其工作性能。刘厚林等[5]通过设置不同导叶时序位置，仿真得到离心泵外特性、隔舌处的压力脉动和叶轮径向力随不同时序位置的变化规律。王文杰等[6]针对两个非标准工况下的导叶式离心泵进行仿真模拟，分析了5个不同导叶时序位置对导叶以及蜗壳内压力脉动的影响规律。谈明高等[7]通过搭建试验平台，测试了8个导叶时序位置正交方案对多级离心泵的外特性及振动性能的影响规律。卢金玲等[8]研究了诱导轮与叶轮时序位置对泵外特性、振动特性，以及空化特性的影响规律。ZHANG等[9]研究了进口具有诱导轮，出口具有径向导叶（RGV）的单级离心泵的水动力特性受时序效应的影响变化规律，发现存在一个既可以提高泵扬程和效率，又可以降低压力脉动强度的最佳位置。LAI等[10]为研究离心泵的时序效应，基于k-omega剪切应力传输模型进行了3D数值计算，发现最佳扩散器安装角为25°，此时作用在叶轮上的总压力损失和径向力最小。TAN等[11]研究了五级离心泵中叶轮的时序效应和由时序效应引起的泵级之间的叠加效果，发现泵的扬程和效率变化不大，而振动频率和振幅变化较大。GU等[12]对叶片扩压器相对于圆形外壳的圆周不同时序位置进行了研究，基于计算流体动力学的最小熵产生理论，采用流动损失可视化方法来描述由时序位置引起的损失。WANG等[13]为分析叶片扩压器相对于环形蜗壳的位置对离心泵性能特性和压力脉动的影响，在三个不同的相对位置进行了实验测试，并得出了最佳时序位置。JIANG等[14]通过设置不同的扩压器叶片与隔舌的相对位置，研究了时序位置对离心泵非定常压力波动和叶轮径向力的影响。QU等[15]研究了带有入口导叶的离心泵的时序效应，发现时序位置对泵的扬程和效率影响不大，而对泵内的压力波动和流场的影响却很明显。可见，时序位置对泵的性能影响较大。

上述文献多数仅考虑泵转子或者定子单一时序位置变化对泵性能的影响，而有关井用多级潜水泵叶轮与空间导叶的时序位置匹配关系研究较少。因此，本文构建两级潜水泵模型，设计4种不同时序位置，通过仿真模拟与试验验证，研究次级叶轮与次级空间导叶的时序位置匹配关系对井用多级潜水泵性能的影响以及变化规律。此研究对改善井用多级潜水泵的水力性能，提高其使用效率，研发新泵型提供参考。

1 几何模型

以200QJ20型井用多级潜水泵为研究对象，其基本水力设计参数为：额定流量Qd为20 m3/h；单级扬程Hs为13.5m；转速n为2850 r/min；比转数ns为10.09（根据单级扬程计算）。

原有模型泵叶轮叶片数Z1为6，叶片6枚均布，自吸入口方向看，叶片逆时针旋转，流道表面光滑。叶片进口厚度为2 mm，出口厚度为2.5 mm。空间导叶与径向导叶相比，具有径向尺寸小的优点，与圆柱形导叶相比，具有水力损失小的优点，故中高比转数井用多级潜水泵常采用空间导叶的形式。原有模型泵空间导叶叶片数Z2为5，叶片为扭曲叶片，整体流道过渡光滑。构建的单级泵子午面截线图和三维实体模型分别见图1和图2。

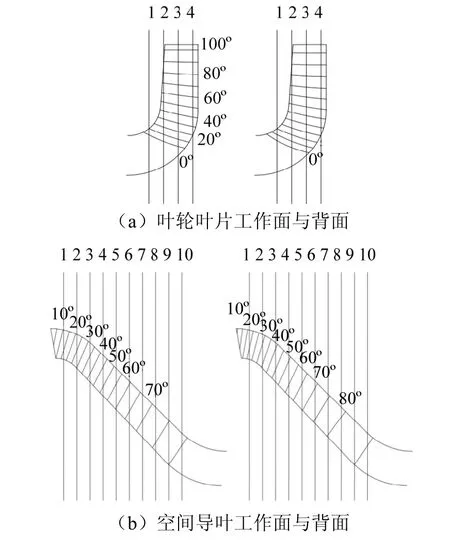
图1 子午面截线图Fig.1 meridian intercept diagram

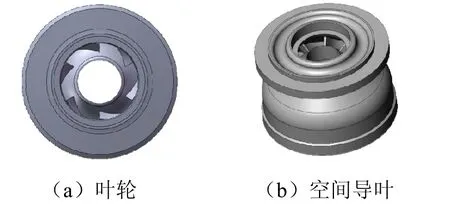
图2 三维实体模型Fig.2 solid 3D model

2 数值模拟

2.1 三维建模

井用多级潜水泵的第一级进口采用无预旋流动，第二级之后进口采用有旋流动，所以第二级的内部流动规律可代表之后的流动规律。同时考虑到计算机数值模拟的求解时间，文中以两级井用潜水泵模型进行分析。为使流体得以充分发展，降低进出口边界条件与结构对进出口回流的影响，将进水段与出水段长度设置为4倍的进出口直径。得到的计算域模型见图3。

图3 计算域模型Fig.3 computational domain model

2.2 网格划分与无关性分析

非结构化网格的节点较为自由，分布任意，生成简单且速度较快，灵活性强，因而能适应各种复杂的几何体，但是存在局部网格质量较差的问题，导致整体网格质量划分不高、数量大、计算求解时间长。结构化网格需要对模型进行分块拓扑，这将导致网格划分较为复杂，耗费时间长，但考虑其节点分布较为规律，所以能更好地节省计算求解时间，可更快达到收敛精度。一般情况下，结构化化网格的质量要优于非结构化网格质量，故文中采用结构化网格划分方法。基于ICEM与TurboGrid软件，对网格进行划分，并对边界层网格进行加密处理，结构化网格质量达到0.3以上。整体模型网格划分及边界层网格加密见图4和图5。

图4 整体模型网格划分Fig.4 meshing of the whole model

图5 边界层网格加密Fig.5 boundary layer mesh refinement

考虑到网格数量对数值计算结果的影响很大，故进行网格无关性分析，其结果见表1。将方案2的扬程和效率作为单位1，其他方案的扬程和效率均与方案2作对比。当全流道网格数达到400万时，扬程和效率趋于稳定，方案3与方案4的相对扬程误差为0.25%，相对效率误差为0.17%。考虑到计算时间，最终确定方案3的划分方式作为划分所有模型的标准。

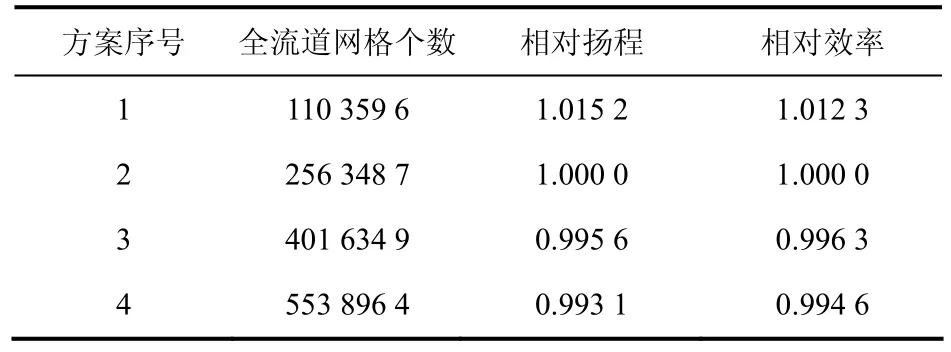
表1 网格无关性分析Tab.1 grid independence analysis

2.3 数值求解设置

考虑湍流流场中时间及空间特征尺度之间的巨大差异，工程上一般采用雷诺时均方程进行求解。雷诺时均方程由N-S方程经过时均化处理后得到，其张量表达式为

式中：ui,j为与坐标轴xi,j平行的速度分量；为速度时均量；为体积力时均值；ρ为介质密度；为压力时均值；ν为运动黏度；为速度脉动量。

对于定常不可压流动，上述方程可以改写为

由于时均化的N-S方程组不封闭，故需要引入湍流模型来封闭该方程组。选用湍流标准k-ε模型，其湍动能k与耗散率ε方程为

式（3）、式（4）中：Gk为由于平均速度梯度产生的湍动能；Gb为由于浮力影响产生的湍动能；YM为可压缩湍流脉动膨胀对总的耗散率的影响。湍流黏性系数。在商用CFD中，一般默认常数为C2ε=1.44，C2ε=1.92，C3ε=0.09，湍动能k与耗散率ε的湍流普朗特数分别为σε=1.0，σε=1.3。

计算域模型（图3）分为旋转区域与静止区域。旋转区域为叶轮，转速设置为2850 r/min，静止区域为进出口段与空间导叶。将进口边界条件设置为压力进口，压力大小为一个大气压，出口边界条件设置为相应工况下的质量流量。壁面为无滑移边界条件和标准壁面函数。旋转区域与静止区域的交互面设置为“Frozen Rotor”，网格关联模式采用GGI模式，整体湍流强度为5%，设置收敛精度为10-4。非定常计算以定常计算的结果为初始条件，将旋转区域与静止区域的交互面设置改为“Transient Rotor Stator”，设置总时间为0.105263 16 s，即旋转5圈，时间步为2.339×10-4s，即每4°计算一步，每5个时间步长输出一次，采用最后一个周期的结果进行数据分析。

2.4 时序方案布置与监测点设置

200QJ20型井用潜水泵叶轮叶片数为6，相邻两叶片夹角为60°，导叶叶片数为5，相邻两叶片夹角为72°。相对于首级叶轮而言，将次级叶轮分别旋转0°或30°（即叶轮相邻两叶片夹角的1/2）。相对于首级空间导叶而言，次级空间导叶分别旋转0°或36°（即空间导叶相邻两叶片夹角的1/2），由上述2种时序位置，组成CL0、CL1、CL2、CL3共4种匹配方案，见表2。

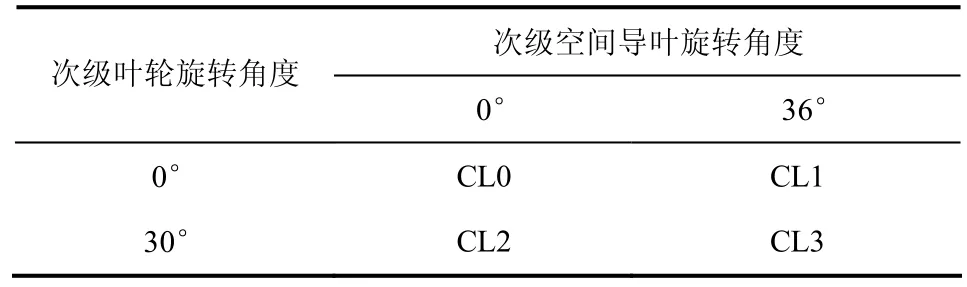
表2 时序位置匹配方案Tab.2 clocking location matching scheme

为分析不同时序位置对压力脉动的影响，在次级叶轮流道轴向中截面靠近进出口区域分别布置监测点Y1和Y2，在次级空间导叶流道轴向中截面靠近进出口区域分别布置监测点Y3和Y4，见图6。

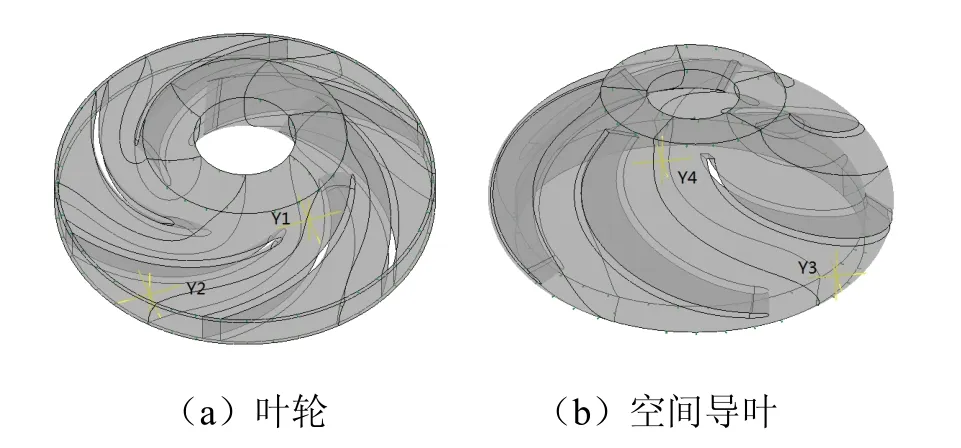
图6 监测点布置Fig.6 layout of monitoring points

3 理论仿真与性能试验对比

3.1 试验平台搭建

为了验证模型和仿真参数设置的合理性，搭建井用潜水泵性能试验测试平台，见图7。在井用潜水泵出口处放置压力传感器采集压力数据，为减小管路弯道对流量测量精度的影响，在管道平直部分

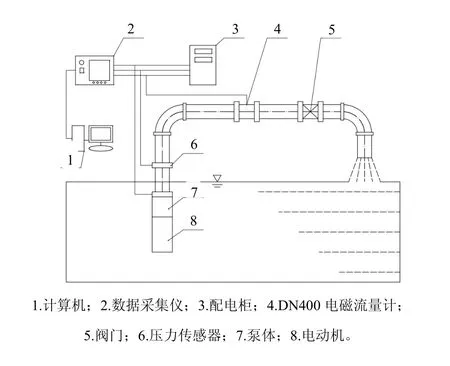
图7 泵性能试验平台装置示意Fig.7 schematic of pump performance test platform

中段放置DN400电磁流量计采集流量数据，压力和流量等参量数据经数据采集仪传给计算机进行处理。试验从零流量开始，然后逐渐增大阀门开度，在流量稳定时采集相应数据。为了减小试验误差，将试验多次重复测量，并将算术平均值作为最终测量结果。

3.2 理论仿真与性能试验对比分析

在Function Calculator中，Function设置为 mass FlowAve，Location设置为进出口，Variable设置为TotalPressureinStnFrame，即可获得出口压力pout与进口压力pin，其扬程为

同理，将Function设置为torque，Location设置为叶轮旋转区域，即可获得叶轮所受力矩M，根据叶轮转速求得叶轮角速度ω，其水力效率为

将仿真模拟得到的外特性曲线与试验结果进行对比分析，见图8，由于模型为两级模型，而试验模型为6级，所以需将仿真模拟得到的二级数据换算成6级。由图8可以看出，试验扬程略高于模拟扬程，试验效率略低于模拟效率，但两者的变化趋势基本一致，即表明仿真模拟结果可以完全替代试验测试结果，可很好地预测井用潜水泵的实际性能。在标准工况下，模拟扬程比试验扬程低3%，模拟效率比试验效率高3.4%。数据存在差异的主要原因有：一是受计算机配置与网格划分方式及数量的影响；二是受模型简化的影响，比如未考虑间隙问题。

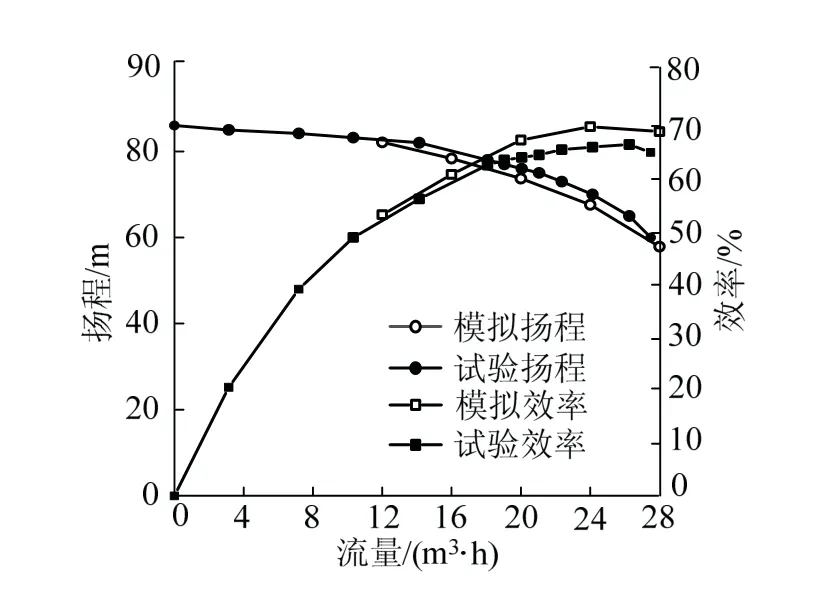
图8 泵性能试验结果与数值模拟结果对比Fig.8 comparison of pump performance test results with numerical simulation results

4 不同时序位置结果仿真分析

4.1 外特性分析

标准工况下不同时序位置的扬程效率曲线对比分析，见图9。由图9可知，时序位置的匹配关系对扬程效率均有影响。在时序位置CL2处扬程和效率最大，扬程为24.3 m，效率为75.4%，在时序位置CL3处扬程和效率最小，扬程为23.8 m，效率为74.9%，其最大扬程与最小扬程相差0.5 m，最大效率与最小效率相差0.5%，即时序位置CL2的外特性最好。考虑到泵的实际内部流动非常复杂，为进一步探究内部流动特性变化规律，现对次级叶轮与次级空间导叶内部压力、速度流线和压力脉动进行对比分析。

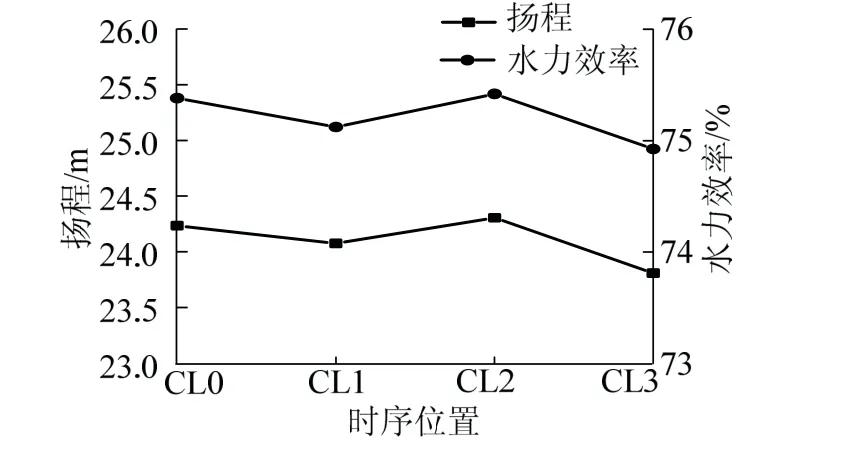
图9 不同时序位置外特性对比Fig.9 comparison of external characteristics of different clocking positions

4.2 压力分布分析

4种时序位置的次级叶轮与次级空间导叶的中截面的压力展开分布见图10。由图10可知，4种不同时序位置的次级压力分布规律基本一致。在叶轮进口区域压力最低，最小静压为180 kPa，由于叶轮旋转做功，在叶轮出口区域压力逐渐升高，流经空间导叶导流，最大静压达到376.5 kPa。从叶片的背面到同一流道的工作面压力逐渐升高，形成这种压力差的原因是相对速度的差异。在导叶进口边附近均出现点状高压区，如图10中红色圆圈标记所示，这是由于流体从叶轮出口进入到空间导叶时，碰撞导叶进口边而导致的。导叶工作面由于受到来流冲撞，贴近工作面处均生成由窄到宽的高压区域。在导叶工作面附近，时序位置CL2的高压区面积最大，如图10中红色矩形标记所示，这也正是时序位置CL2的扬程和效率高于其他时序位置的原因。时序位置CL3的高压区面积最小，导致了其扬程和效率与其他时序位置相比较低。在叶轮进口区域，虽然时序位置CL0的低压区面积最小，但是时序位置CL2高压区的优势弥补了低压区的劣势，占据主导因素，所以其扬程和效率较高。

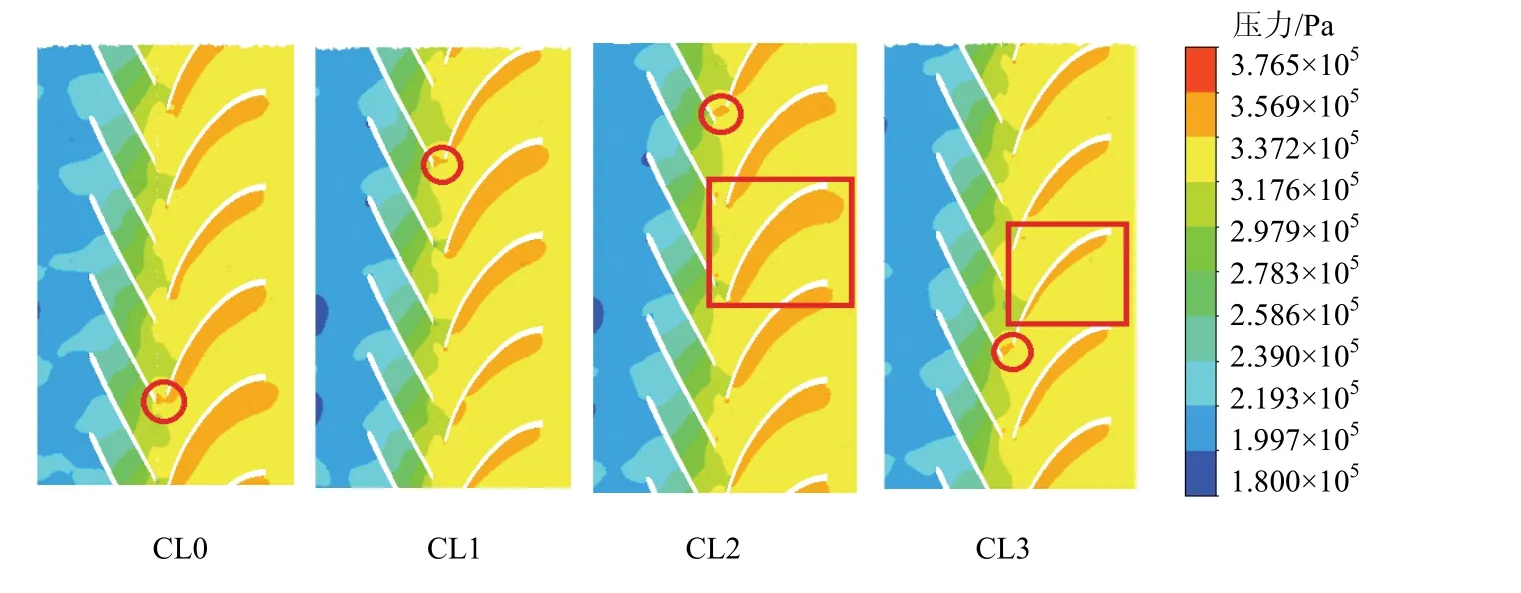
图10 不同时序位置次级叶轮与次级空间导叶中截面压力展开分布Fig.10 pressure expansion distribution in the middle section of secondary impellers and secondary space guide vanes at different clocking positions

4.3 速度流线分析

4种时序位置的次级叶轮与次级空间导叶的中截面的速度流线见图11。由图11可知，4种不同时序位置的速度流线变化规律基本一致，其最小流速为0.0014 m/s，出现在时序位置CL1，最大流速为21.03 m/s，出现在时序位置CL3。在叶轮进口区域，流体在叶轮叶片进口边均出现不同程度的分流。在叶轮叶片的工作面处均出现小部分的低速区，这也是导致上述压力分析中叶片两面存在压力差的原因。在导叶背面，均出现涡流区域，这是由于流体在叶轮的作用下，大部分沿着导叶的工作面流动，发挥了导叶引流的作用，但在导叶背面的一小部分流体容易产生脱离，进而形成涡流区域。时序位置CL2相比于时序位置CL0与时序位置CL1，在叶轮流道区域流线更加平顺，由此可见，当次级叶轮相对于首级叶轮旋转30°时，可以改善叶轮流道内的流动情况。时序位置CL2相比于时序位置CL3，在导叶背面的流线较为稀疏，故涡流区域相对较小，且在时序位置CL3的导叶背面会形成较多二次涡流区域，加大了能量损耗，这也是导致时序位置CL3的扬程和效率较其他时序位置低的原因之一。二次涡流区域如图11中时序位置CL3的红色标记所示。

图11 不同时序位置次级叶轮与次级空间导叶中截面速度流线展开Fig. 11 unfold of velocity streamline in the middle section of secondary impeller and secondary space guide vane at different clocking positions

4.4 压力脉动分析

在分析了内部压力分布规律的基础上，进一步探究不同时序位置下的压力脉动规律，引入无量纲化压力脉动系数CP，使其更具实用性和普遍性。

式中：p为某一时刻下监测点位置处的压力，Pa；为一个周期内监测点处压力的平均值，Pa；ρ为水泵所输送的介质的密度，kg/m3；u2为叶轮出口圆周速度，m/s。

次级叶轮一个流道内的监测点在第5个旋转周期内的压力脉动时域、频域特性见图12和图13。

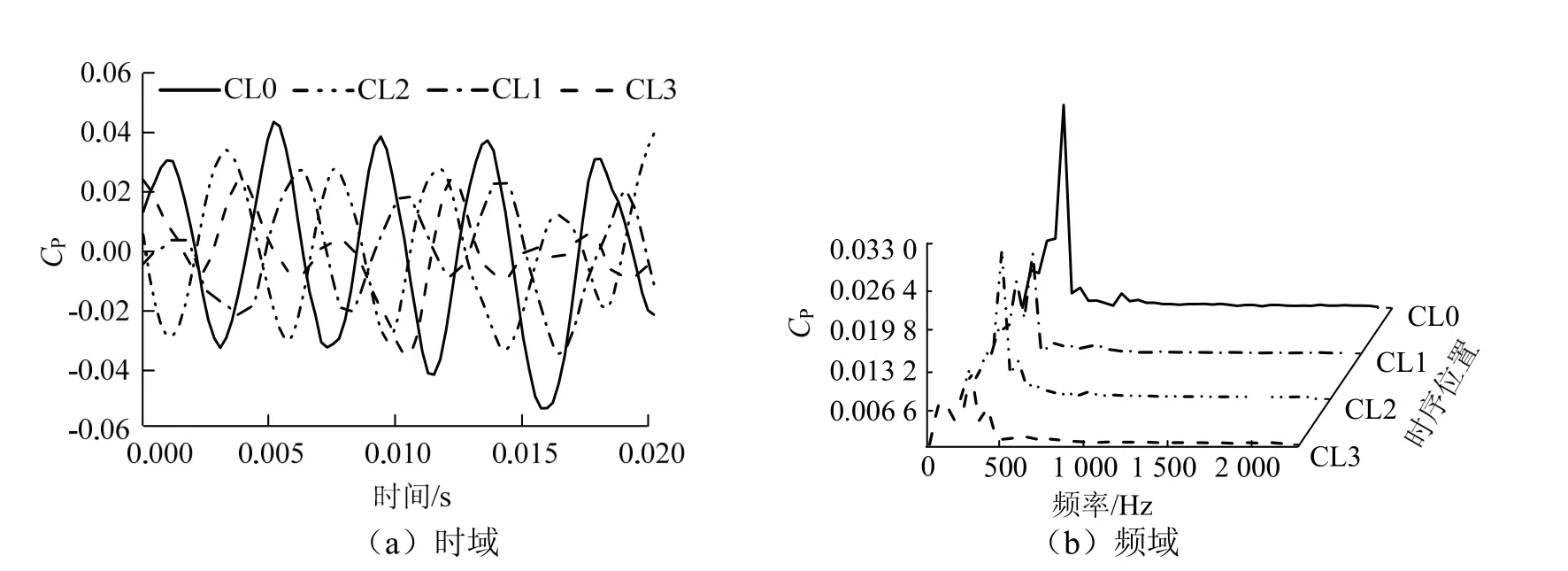
图12 监测点Y1压力分布Fig.12 time domain and frequency domain distribution of pressure fluctuation at Y1 monitoring point

图13 监测点Y2压力分布Fig.13 time domain and frequency domain distribution of pressure fluctuation at Y2 monitoring point

从图12（a）中可以看出，在叶轮流道进口处到出口处的监测点Y1和Y2处，压力脉动周期性变化趋势基本一致，在一个周期中出现了5次波峰，这与导叶的叶片数保持一致，这是由于叶轮叶片在旋转过程中与导叶叶片发生了强烈的动静干涉作用。各处峰值的极值存在差异，时序位置CL0的峰值极值最大，时序位置CL3的峰值极值最小。时序位置CL2与时序位置CL3的相位明显不同于时序位置CL0与时序位置CL1，且时序位置CL2与时序位置CL3的波峰位置对应时序位置CL0与时序位置CL1的波谷，形成一个循环周期，表明不同时序位置可以改变叶轮进口处压力脉动的相位值。

图12（b）为该监测点Y1经FFT变换得到的压力脉动频域图。由图可知，不同时序位置下压力脉动的主导频率均为一倍导叶叶频附近，这说明动静干涉作用占主导影响因素。不同时序位置下的压力脉动幅值大小关系为：CL0＞CL2＞CL1＞CL3，即时序位置CL0压力脉动幅值最大。与时序位置CL0处的压力脉动幅值相比，时序位置CL2、时序位置CL1以及时序位置CL3的压力脉动幅值分别降低了26.5%、50.6%和64%，表明不同时序位置可以改变叶轮进口压力脉动幅值大小。

图13（a）为次级叶轮靠近出口的Y2监测点的不同时序位置的压力脉动时域图。由于叶轮旋转对流体做功，静压值上升，所以叶轮出口处的监测点的压力脉动幅值较叶轮进口处的压力脉动幅值明显增大。叶轮出口压力脉动监测点的压力脉动与叶轮进口处较为相似，但时序位置CL0和时序位置CL3的波峰与时序位置的CL1与时序位置CL2的波谷相对应，表明不同序位置可以改变叶轮出口处压力脉动的相位值。

由图13（b）可以看出，不同时序位置下的压力脉动幅值大小关系为：CL0＞CL2＞CL1＞ CL3，即时序位置CL0压力脉动幅值最大。与时序位置CL0处的压力脉动幅值相比，时序位置CL2、时序位置CL1以及时序位置CL3的压力脉动幅值分别降低了23%、40.2%和40.7%，表明不同时序位置可以改变叶轮出口压力脉动幅值大小。由此可以看出，当时序位置为CL3时，叶轮流道进出口压力脉动幅值均为最小，对泵的性能影响最小。

次级空间导叶一个流道内的监测点在第5个旋转周期内的压力脉动时域和频域特性，见图14和图15。

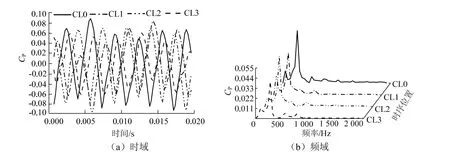
图14 Y3监测点压力脉动时域与频域分布Fig。 14 time domain and frequency domain distribution of pressure fluctuation at Y3 monitoring point

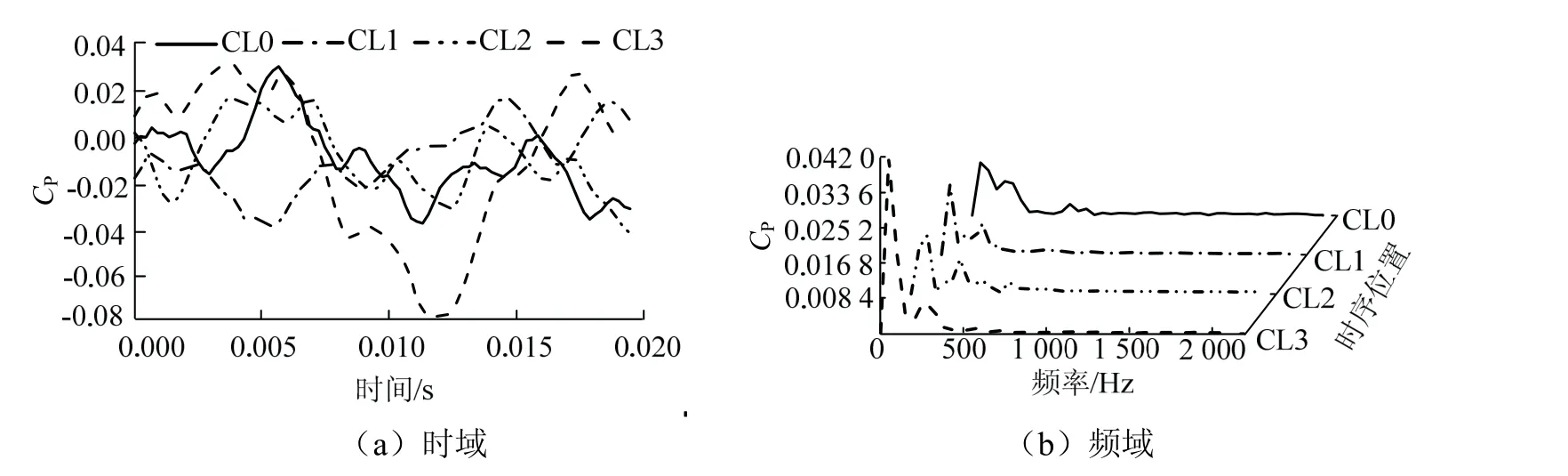
图15 Y4监测点压力脉动时域与频域分布Fig。15 time domain and frequency domain distribution of pressure fluctuation at Y4 monitoring point

从图14（a）中可以看出，在空间导叶流道进口处到出口处的监测点Y3、Y4处，压力脉动周期性变化趋势基本一致，在一个周期中出现了6次波峰，这与叶轮的叶片数保持一致，同样是由于强烈的动静干涉作用导致。与叶轮出口监测点一致，时序位置CL0和时序位置CL3的波峰与时序位置的CL1与时序位置CL2的波谷相对应，表明不同时序位置可以改变导叶进口处压力脉动的相位值。

由图14（b）可知，不同时序位置下压力脉动的主导频率均为一倍叶轮叶频附近。这说明动静干涉作用还是占主导影响因素。不同时序位置下的压力脉动幅值大小关系为：CL0＞CL2＞ CL1＞CL3，即时序位置CL0压力脉动幅值最大。与时序位置CL0处的压力脉动幅值相比，时序位置CL2、时序位置CL1以及时序位置CL3的压力脉动幅值分别降低了3.6%、19.1%和29.8%，表明不同时序位置可以改变空间导叶进口压力脉动幅值大小。与叶轮上的监测点相比，导叶上的监测点在次频处的脉动幅值逐渐增大，表明轴频的影响越来越大。

图15（a）为次级空间导叶靠近出口的监测点的不同时序位置的压力脉动时域图。流体经过空间导叶，静压下降，所以空间导叶出口处的监测点的压力脉动幅值较空间导叶进口处的压力脉动幅值明显减小。由图可知，靠近导叶出口的监测点的压力脉动规律性明显减弱，这可能是多处动静干涉耦合导致的结果。

由图15（b）可以看出，不同时序位置下的压力脉动幅值在轴频的整数倍频率附近达到最大值，这是由于在导叶出口处，远离动静干涉的影响，轴频的影响占主导因素。不同时序位置下的压力脉动幅值大小关系为：CL3＞CL1＞CL0＞CL2，即时序位置CL3压力脉动幅值最大。与时序位置CL3处的压力脉动幅值相比，时序位置CL1、时序位置CL0以及时序位置CL2的压力脉动幅值分别降低了59.5%、69.7%和73.2%，表明不同时序位置可以改变空间导叶出口压力脉动幅值大小。监测点Y4压力脉动幅值大小关系与其他3个监测点压力脉动幅值大小关系不同，是因为导叶出口处受到多处动静干涉耦合的影响。

5 结论

（1）叶轮与空间导叶时序位置匹配关系对井用多级潜水泵的外特性有一定影响，当时序位置不同时，最大扬程与最小扬程相差0.5 m，最大效率与最小效率相差0.5%。当次级叶轮旋转1/2叶轮叶片夹角，次级空间导叶不变化时，扬程效率最大。当次级叶轮旋转1/2叶轮叶片夹角，次级空间导叶旋转1/2空间导叶叶片夹角时，扬程效率最小。即从外特性的角度来看，时序位置CL2最佳。

（2）当次级叶轮旋转1/2叶轮叶片夹角，次级空间导叶不变化时，贴近导叶工作面的高压区最大，在叶轮流道区域流线更加平顺。当次级叶轮旋转1/2叶轮叶片夹角，次级空间导叶旋转1/2空间导叶叶片夹角时，贴近导叶工作面的高压区最小，导叶背面形成二次涡流区域。

（3）叶轮进出口以及导叶进口的压力脉动较为规律，导叶出口的压力脉动规律性明显减弱。叶轮与空间导叶时序位置的匹配可以改变叶轮进出口以及导叶进口的相位与压力脉动幅值。当次级叶轮旋转1/2叶轮叶片夹角，次级空间导叶旋转1/2空间导叶叶片夹角时，叶轮进出口以及导叶进口的压力脉动幅值明显降低，但导叶出口处的压力脉动幅值明显增大。即从压力脉动的角度来看，时序位置CL3较于其他时序位置可明显减小次级叶轮进出口处以及次级导叶进口处的压力脉动幅值，但同时会增大次级导叶出口处的压力脉动幅值。