BFPC结合面参数神经网络预测及其对机床动态性能影响

2023-06-10于英华李佳美沈佳兴郑思贤

辽宁工程技术大学学报（自然科学版） 2023年2期

于英华，李佳美，徐平，沈佳兴，郑思贤

（辽宁工程技术大学机械工程学院，辽宁阜新 123000）

0 引言

数控机床的高速化、高精度化和高自动化对其基础件的静、动、热态特性提出了越来越高的要求[1-4]。相关研究表明，BFPC这种新型复合材料可以有效地提高机床基础件的如上性能[1,4-5]。而BFPC机床基础件中通常包含BFPC结合面。已有研究表明，结合面的特性对由此形成的机械结构整体的静、动、热态性能具有显著影响[1,6-8]。为此研究BFPC结合面参数预测及其对机床动态性能影响具有重要意义。

迄今为止，国内外对机床结合面的研究多集中于对传统机床材料——铸铁和钢材料的结合面参数识别及应用研究。RAFFA等[8]运用均匀化和渐近技术相结合的方法，建立了基于接触弹簧模型的结合面切向和法向接触刚度模型，并通过与已有的相关理论分析和实验研究结果进行对比，证明了所建模型的正确性。朱坚民等[9]建立了铸铁工作台-床身滑动导轨结合面动态特性参数的神经网络预测模型，以该模型为基础对机床的前四阶模态进行仿真分析，并通过实验研究验证了所建模型的正确性。张学良等[10]以铸铁-钢结合面为研究对象，建立了基于等效横观各向同性的固定结合面虚拟材料参数模型，并将其应用于哑铃形组件的模态仿真分析，最后通过与相应的实验研究结果进行对比，证明了该建模方法的正确性和优越性。魏若程等[11]以超精密飞切机床为研究对象，探讨了基于虚拟材料法的机床结合面动态特性参数建模，并将该模型引入机床整机建模及其动力学特性仿真分析，证明虚拟材料模型较传统的弹簧-阻尼模型具有更高的精度。然而，目前国内外对混凝土类材料机床基础件结合面的相关研究还鲜见报道。

本文探究结合面表面粗糙度和预紧力对BFPC固定结合面虚拟材料动态特性的影响规律，并建立相应的神经网络预测模型。以BFPC数控机床龙门框架组件为例，通过折中规划多目标优化设计方法，优化BFPC固定结合面虚拟材料参数，确定最优结合面表面粗糙度和预紧力。最后，基于虚拟材料的仿真分析方法，研究结合面对BFPC数控机床龙门框架组件动态特性的影响，及结合面虚拟材料参数优化对提高机床基础件动态特性的有效性。

1 结合面动态特性参数模型建立

1.1 模型构建

相关研究表明，结合面的动态特性参数受多种因素影响，且很多因素是非线性的、模糊的。神经网络有良好的非线性映射能力，适用于处理此类问题[9]。为此运用神经网络理论，建立BFPC固定结合面动态特性参数与结合面粗糙度及预紧力之间的关系模型。根据研究内容数据结构，确定神经网络拓扑结构，见图1。其中输入量为结合面粗糙度与预紧力，输出量为结合面法向和切向的刚度及阻尼。

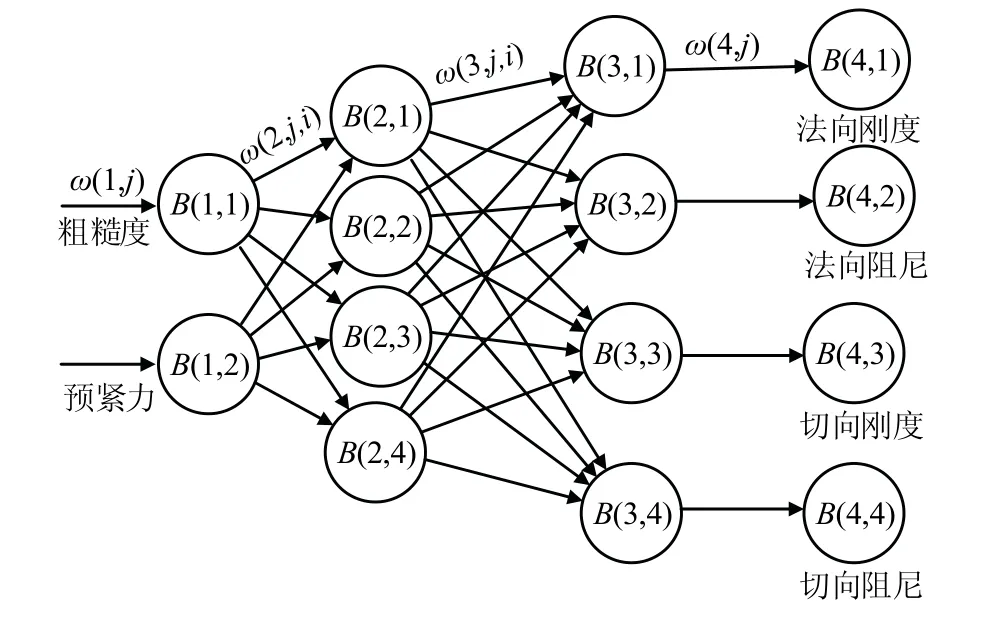
图1 神经网络预测模型拓扑结构Fig.1 topological structure of neural network prediction model

线性化后的训练样本为Tin和Tout。设节点的输入为Tr(k,j)，输出为Tc(k,j)，偏差为B(k,j)，第k-1层与k层之间的权重为ω(k,j,i)，其中k为神经网络的层数（k=1,2,3,4)，j为神经网络第k层的节点序号，i为第k层第j个节点对第k-1层的第i个节点的对应权重标识号。由此可得

式中：jk-1为第k-1层的节点数；f为神经单元的作用函数，

输出各节点的误差为

式中，n为输出节点前一层对其有输入的节点数。

输出层各节点的误差为

中间层各节点的误差为

误差梯度为

总误差梯度为

则修正权重为

中间层各节点的偏差为

节点的偏差梯度为

总偏差梯度为

神经网络偏差的修正为

按式（11）～式（14）进行迭代计算并不断修正神经网络预测模型的权重与偏离，直到模型收敛即可最终确定BFPC结合面动态性能参数神经网络预测模型。

1.2 实验数据的测定

根据前期研究实验方法和原理[1,12]，采用图2（a）所示的自制模具，制作规格为150 mm×150 mm×100 mm的上、下试件，见图2（b）和图2（c）。如图2（d）所示，将螺栓3通过预埋于上试件中的空管2与嵌入下试件的钢制螺母5旋合，从而使上试件1和下试件4连接为一体，形成尺寸为150 mm×150 mm的BFPC结合面。通过切削加工获得表面粗糙度分别为3.2 μm、6.3 μm、12.5 μm和25 μm的4种上下试件形成的结合面。

图2 试件制作过程Fig.2 process of making test pieces

采用图3的测试系统测试并计算[12]表1中20组结合面表面粗糙度和预紧力下的BFPC固定结合面的法向和切向阻尼与刚度，结果见表1。

表1 结合面的阻尼与刚度Tab.1 damping and stiffness of joint surface

图3 实验测试Fig.3 experimental test

1.3 神经网络训练

以表1中的前14组数据通过Matlab软件中的neural network start工具训练神经网络，以表1中第15～17组数据对神经网络是否过拟合进行检测，以表1中最后3组数据对神经网络的泛化能力进行检查。选择如图4所示的4个中间层的双层前馈网络的?Levenberg-Marquardt的训练法，当网络误差满足要求时训练结束，神经网络各节点的偏差及节点间的权重见表2。

表2 神经网络节点的偏差与权重Tab.2 deviation and weight of the neural network nodes

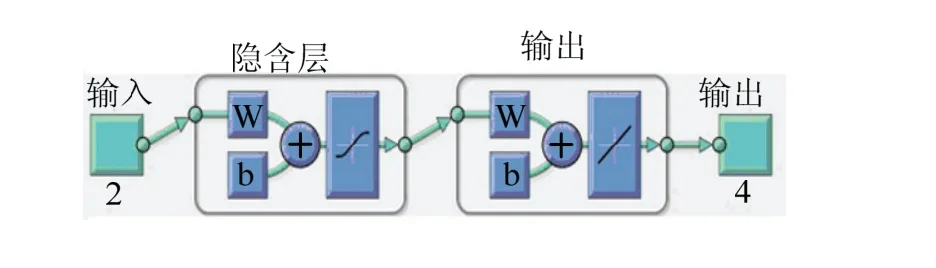
图4 神经网络预测模型Fig.4 neural network prediction model

为了验证所建立神经网络模型的正确性，将训练完成后获得的神经网络代入回归分析，得出的各单项数据拟合程度均大于0.96，总数据拟合程度达0.98，这说明所建立的神经网络预测模型具有较高的精确度。

2 结合面虚拟材料参数确定和优化

“虚拟材料法”是在仿真分析建模时，以黏弹性材料代替结合面的一种等效建模方法，以虚拟材料的虚拟层厚度、剪切模量、弹性模量、泊松比等参数对结合面进行等效模拟。当利用虚拟材料法等效替代结合面，对由该结合面形成的组装结构件进行动态特性有限元仿真分析建模时，虚拟材料与两接触体之间是通过绑定方式固定在一起的[10-11,13]。

根据文献[12]，利用前述建立的神经网络预测模型，依据接触面表面粗糙度和预紧力预测出BFPC结合面法向和切向刚度及阻尼后，即可以计算确定BFPC结合面虚拟材料参数。

2.1 BFPC龙门框架及静态特性

选取图5的数控龙门加工中心龙门框架为研究原型，它是由两个铸铁立柱及一个铸铁横梁通过螺栓连接而成的组件。在横梁和立柱之间的连接处存在着铸铁固定结合面。由此原型通过拓扑优化设计得到的BFPC龙门框架见图6[4]，该龙门框架由BFPC横梁、两个立柱、立柱的预埋件和螺栓连接而成。在横梁和立柱之间的连接处存在着BFPC固定结合面。

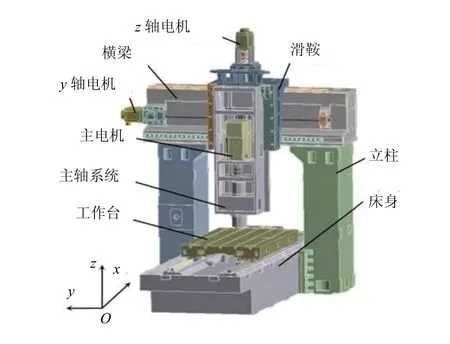
图5 原型数控龙门加工中心Fig.5 prototype CNC gantry machining center

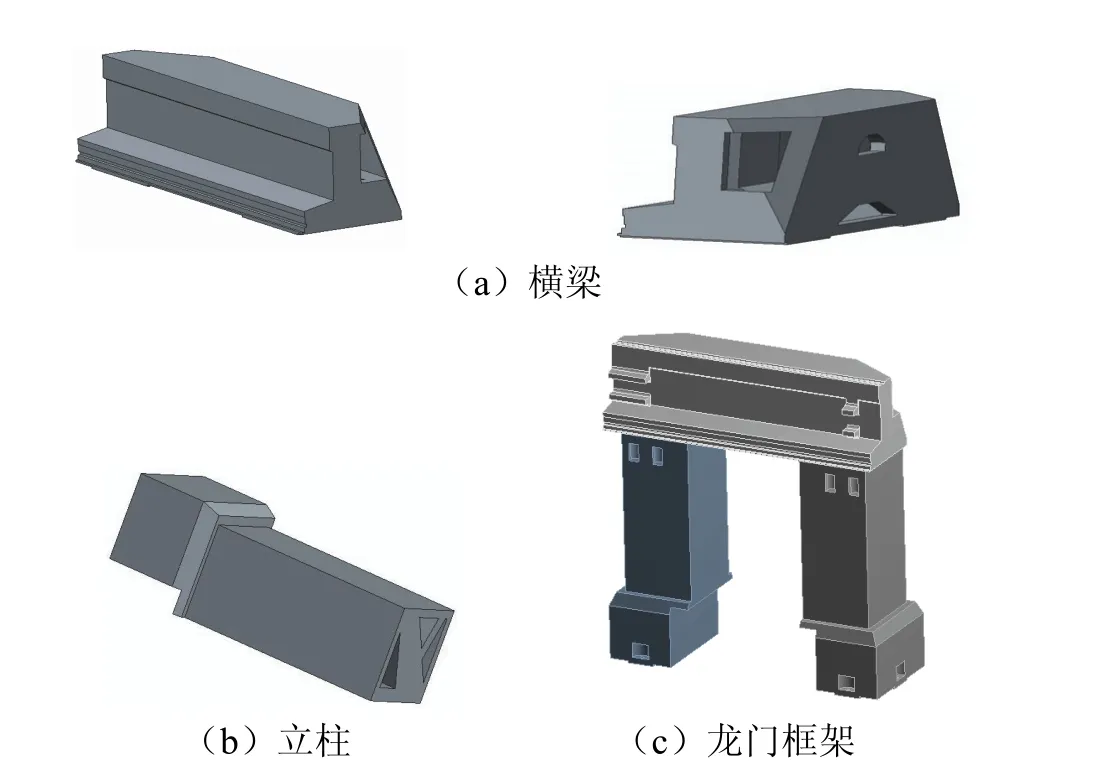
图6 BFPC龙门框架Fig.6 BFPC gantry frame

以数控机床采用端铣刀铣削平面为典型工况，采用直径Φ300 mm、12个刀齿的端铣刀，铣削宽取200 mm，轴向切深取4 mm，切削速度取100 m/min，每齿进给量取0.1 mm。通过切削力经验公式计算出切削力，并考虑刀具位于横梁的中间位置，运用有限元仿真分析方法对数控机床龙门框架的静态特性进行分析，最终得到数控机床龙门框架的最大变形为0.0698 mm，最大应力为28.736 MPa[4]。

2.2 结合面虚拟材料参数优化

（1）优化问题描述

为保证BFPC龙门框架在满足静态性能前提下其动态性能最优，采用折中规划多目标优化设计方法[14]，对结合面虚拟材料参数进行优化。优化时以BFPC龙门框架前三阶模态固有频率加权值最大，在x、y、z三个方向的谐响应最大位移加权值最小为目标函数，以最大位移小于原型龙门框架的最大位移及最大应力小于BFPC许用应力为约束条件，以结合面表面粗糙度r和预紧力l为设计变量。优化模型为

式（15）～式（16）中：θi为各优化目标的权重，当i取1,2,3,4,5,6时，θi分别取0.2，0.2，0.1，0.2，0.1，0.2；Λi为各阶固有频率，Hz；Λimax为计算过程中出现的各阶固有频率的最大值，Hz；Λimin为计算过程中出现的各阶固有频率的最小值，Hz；U为BFPC龙门框架最大位移，mm；Uct为原型龙门框架最大位移，0.0698 mm；σ为最大应力，MPa；[σs]为BFPC的许用应力，取129 MPa[15]；Ut为t方向的最大谐响应，mm；Utmax为t方向的的最大谐响应计算值，mm；Utmin为t方向的最小谐响应计算值，mm。

（2）优化过程

依据图6建立含有虚拟材料层的BFPC龙门框架仿真分析模型，在横梁与立柱的结合面处通过布尔运算的方法赋予厚为1 mm的模拟虚拟材料层。

将所建模型导入ABAQUS进行装配并进行网格划分，网格选择C3D8类型的四面体结构，网格划分模型见图7。

图7 划分网格的BFPC龙门框架Fig.7 BFPC gantry frame with grid division

虚拟层通过绑定方式与立柱和横梁约束为一体。对立柱底面的x、y、z三向平移自由度施加约束，按照2.1节中分析得到的载荷，对BFPC龙门框架添加载荷。龙门框架中的虚拟材料结合面性能参数赋值需依据选取的结合面表面粗糙度和预紧力，根据由神经网络预测模型预测出的结合面的法向和切向刚度与阻尼，再根据文献[12]确定剪切模量、泊松比、密度和弹性模量。对虚拟材料进行方向指派，保证虚拟材料弹性属性的1轴与结合面的法向轴平行，见图8。除了虚拟材料层以外，龙门框架的其他实体材料的参数取值参照BFPC材料[4-5]。

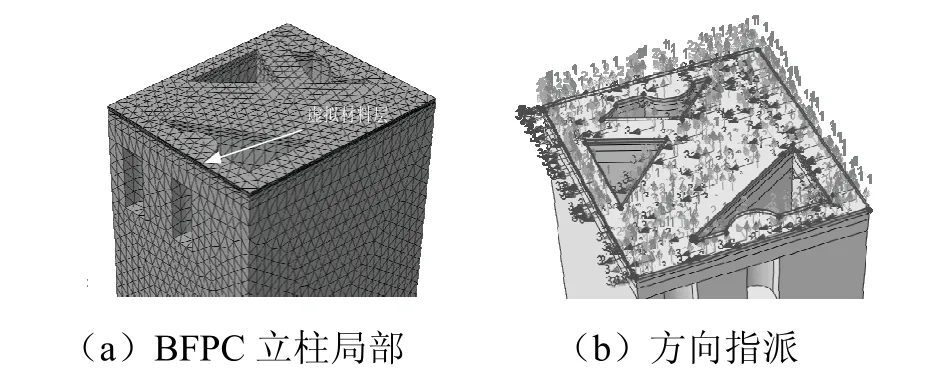
图8 虚拟材料的方向指派Fig.8 direction assignment of virtual material

鉴于无法直接通过ABAQUS进行虚拟层参数优化，联合运用ABAQUS、ISIGHT和MATLAB解决此问题。

（3）优化结果

按照上述优化方法得到结合面最优的表面粗糙度和预紧力分别为6.3μm和0.72 MPa，对应的虚拟材料参数见表3。

表3 虚拟材料参数优化结果Tab.3 optimization results of virtual material parameters

3 结合面对龙门框架动态特性的影响

（1）考虑结合面的龙门框架动态特性分析

对最优虚拟层参数的龙门框架前三模态和谐响应进行分析，结果见图9。

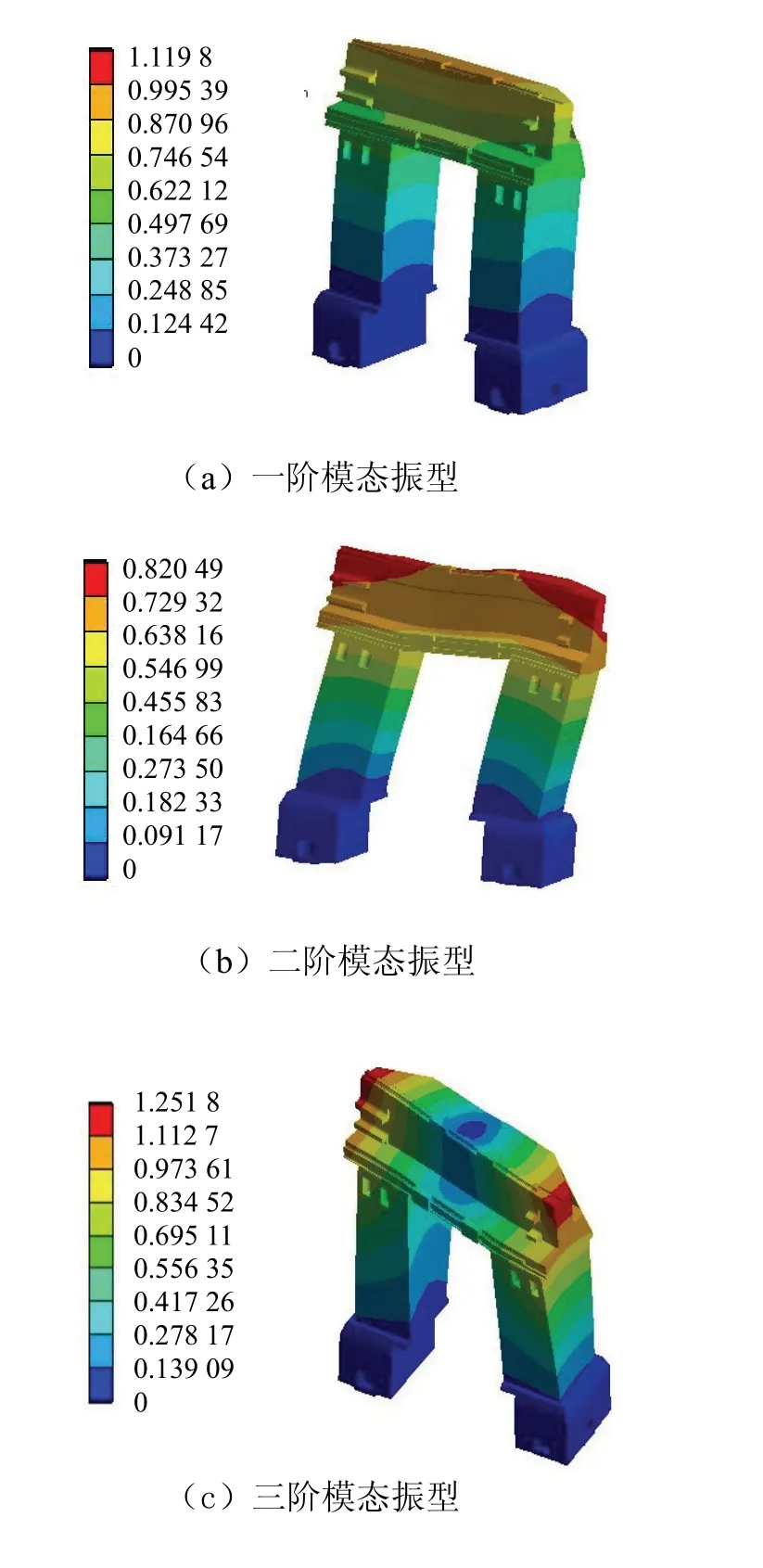
图9 优化结合面参数的龙门框架动态特性Fig.9 dynamic characteristics of gantry frame with optimized joint parameters

表1中粗糙度Ra6.3、预载荷0.8 MPa的结合面参数与最优表面粗糙度和预紧力较为接近，为对比分析，对此组结合面的BFPC龙门框架动态特性也进行仿真分析，得出前三阶模态振型与最优化表面参数的龙门框架相同，限于篇幅，动态分析图从略，仅将前三阶模态的固有频率和在三个方向的谐响应最大振幅绘于柱状图10。

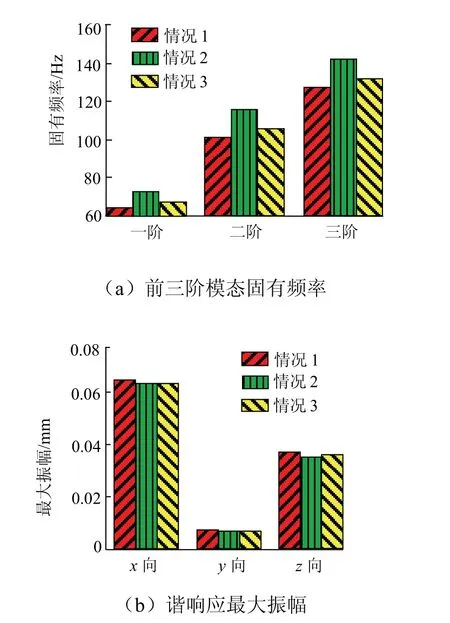
图10 三种BFPC龙门框架动态特性Fig.10 dynamic characteristics of three BFPC gantry frames

（2）不考虑结合面的BFPC龙门框架动态特性分析

当不考虑结合面的影响，分析BFPC龙门框架的动态特性时，即将龙门框架中横梁与立柱之间的固定结合面简化为刚性连接，其它分析过程同考虑结合面的BFPC龙门框架。分析得到BFPC龙门框架的前三阶模态振型同考虑结合面的龙门框架。前三阶模态的固有频率和在三个方向的谐响应最大振幅的柱状图见图10，图中情况1为未经优化的虚拟层参数的龙门框架前三阶模态，情况2为不考虑结合面的龙门框架前三阶模态，情况3为最优虚拟层参数的龙门框架前三阶模态。

（3）对比分析

由图10可见，与不考虑结合面的BFPC龙门框架相比，考虑结合面龙门框架的前三模态的固有频率分别降低10.1%、11.6%和9.2%，在x、y、z三个方向的谐响应的最大振幅分别增加2.7%、3.0%和5.4%；而对结合面表面参数进行优化后，相较于不考虑结合面的BFPC龙门框架，考虑结合面的龙门框架前三模态的固有频率分别降低6.1%、8.6%和6.7%，在x、y、z三个方向的谐响应的最大振幅分别增加0.3%、1.4%和2.3%。即通过对结合面参数进行优化，可使结合面对龙门框架在前三模态固有频率的不良影响分别降低4%、3%和2.5%，对在x、y、z三个方向的谐响应的不良影响分别降低2.4%、1.6%和3.1%。