多子带雷达信号融合噪声抑制方法
2023-06-10蒋伊琳唐三强陆满君张莉婷
蒋伊琳,唐三强,陆满君,张莉婷
(1. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001;2. 哈尔滨工程大学 先进船舶通信与信息技术工业和信息化部重点实验室, 黑龙江 哈尔滨 150001;3. 上海无线电设备研究所, 上海 200000)
受硬件限制,单一子带系统观测的频带范围受到限制,回波所含目标信息有限,由这些信息反演所得到的图像分辨率也相应受到制约。为了提高距离分辨率需要提高信号带宽,而受制于Nyquist采样定理这将导致发射、接收系统更加复杂,给系统硬件实现增加了很大的难度。随着雷达技术和信息处理技术的发展,为了克服单一子带的局限,多子带融合技术的综合使用逐渐成为一种趋势[1]。
多子带融合的本质是外推预测高低子带之间的空余频段[2]。传统的多频段融合方法可以分为两类:
第一类是非参数方法,不需要目标的先验信息。文献[3]提出了放大间隙数据幅度和相位估计(gapped-data amplitude and phase estimation, GAPES)方法。该方法采用最小二乘法迭代估计未知频谱。仿真和实测数据证实了该方法的有效性,但不适当的初始化可能会使该方法陷入局部最优。文献[4]将不同雷达的相位偏差建模为线性相位和恒定相位。该方法采用全相位快速傅里叶变换(all-phase fast Fourier transform, apFFT)对脉冲压缩后的图像进行相关处理,估计恒定相位和线性相位,但是,apFFT脉冲压缩方式失去了信号初相信息,只能显示小角度范围内的相位信息,在面对大角度相位差距时,会出现跨距离窗现象,造成估计误差。文献[5]提出了一种以稀疏表示为基础的融合算法,通过相干补偿与高分辨率成像相结合的方法来补偿非相干相位,获得高分辨率的逆合成孔径雷达融合图像。
第二类是参数化方法,建立参数化模型,求解相关参数。与非参数方法相比,参数化方法利用了丰富的先验信息,具有更优越的性能。文献[6]提出了一种基于全极点模型的融合方法。该方法分别为较低和较高子带建立前向预测矩阵,然后采用奇异值分解和Akaike信息准则(Akaike information criterion, AIC)估计极点数,并采用最小二乘法求解模型参数。补偿相位偏移后,得到积分频率信号。然而,这种方法在低信噪比下难以确定模型阶数,模型阶数错误对线性模型估计结果会造成极大偏差。文献[7]研究了复合制导体制下多传感器异步信息融合的时间同步和空间配准问题,并提出一种自适应无迹卡尔曼滤波算法,该算法采用预测残差构造状态模型误差统计量,通过自适应因子调整状态模型信息对状态参数估值的贡献,有效控制状态模型噪声异常对状态参数估值的影响。文献[8]提出了一种基于广义似然比(generalized likelihood ratio, GLR)检测的多阶段方法,用于使用稀疏子带测量数据估计目标距离像。文献[9]采用root-MUSIC算法和最小二乘法估计非相干相位(incoherent phase, ICP),然后利用相干处理对不同雷达之间的ICP进行补偿,成功合成了四种光子雷达的雷达回波。文献[10]提出了一种复杂噪声环境下的多雷达子带融合新算法,该算法基于噪声概率密度函数,引入惩罚函数来抑制不同类型的噪声。文献[11]提出了一种基于改进RELAX算法的多频带融合方法,该算法将最大差分准则应用于回波Hankel矩阵的奇异值,以提高计算散射中心数的精度。文献[12]提出了一种基于合成实矩阵奇异值的模型阶数估计方法,合成数据矩阵包括复杂观测数据及其共轭数据,充分利用了现有数据信息,该方法比传统的基于复杂观测数据矩阵的模型阶数估计方法有更好的效果,可以在较低的信噪比下估计模型阶数。文献[13]提出了一种基于多输出变量高斯过程模型的多波段图像融合方法。
本文为了解决全极点模型在低信噪比下模型阶数不准、性能较差的问题,将一种噪声抑制方法引入模型,通过在建立模型过程中对信号Hankel矩阵主奇异值各分量加权和归置等方法,达到抑制噪声的目的,并采用整体前向预测矩阵对全极点模型参数进行整体估计,从而减少计算量。
1 噪声抑制方法
针对文献[6]在低信噪比情况下的不足进行改进,有效提高低信噪比条件下模型参数的估计精度。
将雷达回波信号与发射信号共轭相乘可以得到基带信号,其频率分量与目标上散射中心之间的相对距离成比例。对基带信号进行采样和逆傅里叶变换,以提供目标的距离分辨轮廓。靠近雷达的散射中心具有随频率衰减的散射振幅,而远离雷达的散射中心具有随频率增加的散射振幅。以如下基带信号s(n)[14]为例:
(1)
其中:Ak表示散射点散射强度;fk表示子带起始频率;fn=fk+n·Δf,n∈[0,Nk),Nk为频率步进数;am表示第m个散射中心类型;θm表示第m个散射点的角度。在带宽不是很宽时可以将式(1)表示为全极点模型[15]。以信号s1为例抑制噪声,首先构建如式(2)所示Hankel矩阵:
(2)
其中,L1表示相关窗长度,Hankel矩阵与线性时不变系统的瞬态响应相关联。子空间分解方法利用Hankel矩阵的特征结构来估计线性时不变信号模型的参数[16]。为得到精确的模型参数,通常采用L1=N1/3,当L1较大时虽然能得到更好的分辨率,但是对噪声的适应能力较弱。
对H1矩阵进行奇异值分解[17],得到式(3):
(3)

S1=diag(σ1,σ2,…,σr)
(4)
其中,σi(i=1,2,…,r)为矩阵H1的所有奇异值,且σ1≥σ2≥…≥σr≥0,即S1为奇异值依次减小的对角矩阵。根据奇异值分解原理,分解后得到奇异值依次减小的对角奇异值矩阵S1。其中σi(i=1,2,…,r)代表不同的信号分量。通常接近于零的较小的σi代表噪声分量,较大的σi代表目标散射点分量。将噪声分量对应的σi根据需要取一个较小值或者归置为零,即可实现对噪声的抑制。如此可以得到新的对角奇异值S′1。
再重构恢复出H′1矩阵:
(5)
利用式(5),对矩阵H′1求取矩阵H′1的反对角线元素的平均,即可重构出抑制噪声后的雷达信号序列:
(6)
其中,mn为求解的第n点时H′1矩阵中的反对角线上元素个数,即符合i+j-1=n的H′1(i,j)元素个数,∑H′1(i,j)表示每次对矩阵H′1的反对角线元素求和。
奇异值分解法抑制噪声的步骤总结如下:
1)将雷达回波信号序列s(n)重排成Hankel矩阵;
2)对Hankel矩阵进行奇异值分解,即H=USVΗ,得到奇异值对角矩阵S;
3)根据奇异值跟踪目标和噪声等不同信号分量,然后将噪声分量对应的奇异值归置,即为抑制噪声,得到新的奇异值对角矩阵S′;
4)用新的奇异值对角矩阵S′重构H′矩阵,H′=US′VΗ;
5)将重构的H′矩阵再进行重排,得到抑制噪声后的信号序列s′(n)。
在实际多子带融合过程中,只需对Hankel矩阵进行加权和对噪声分量进行归置即可,不用再恢复出抑制噪声后的信号序列,这里是为了将噪声抑制后信号与原信号进行对比。
2 多子带融合方法
超宽带处理要求每个子带具有一致的频谱信号,即每个子带的全极点模型必须一致。当子带测量值由独立工作的宽带雷达收集时,会出现互相干问题。本文应用相干函数的方法补偿任意数量的子带之间缺乏一致性的问题。
全极点模型是一种用指数函数近似幂指函数的方法,其原理是通过线性模型参数估计逼近非线性信号,算法整体流程如图1所示。
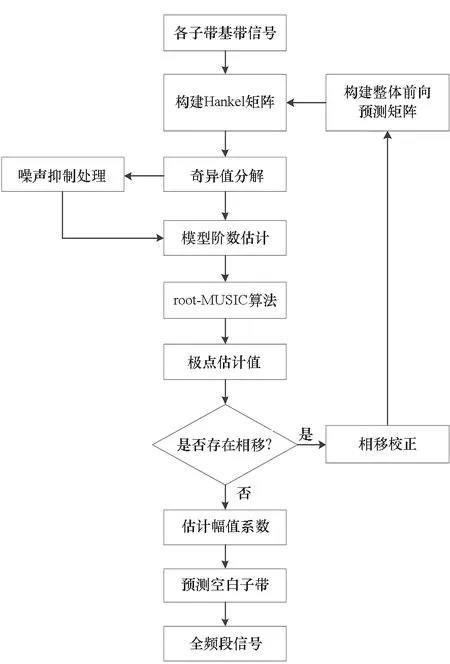
图1 算法整体流程Fig.1 Overall algorithm flow chart
可以将式(1)表示的基带信号表示为如下所示的全极点模型:
(7)
其中,P表示极点数目,ak表示极点幅值系数,pk表示模型的极点。通过将单独的全极点模型拟合到每个子带,并调整模型直到它们一致,可以使子带相互一致。
设计多部同视角观测的独立工作的雷达为例,其起始频率为fi(i=1,2,…,n),频率步进数分别为Ni(i=1,2,…,n),各子带表示为si。根据式(2)构建各子带的Hankel矩阵:
(8)
为了估计各个子带的全极点模型参数,对各个子带的Hankel矩阵按式(3)进行奇异值分解,得到:
(9)
通过分解Hi,可以通过以下四步过程来估计每个子带的全极点模型参数:
步骤1:根据奇异值矩阵Si估计各个子带的模型阶数Pi。
步骤2:Pi将Vi划分为相互正交的信号子空间和噪声子空间。利用root-MUSIC算法估计每个子带的信号极点。
步骤3:根据最小线性二乘拟合来确定全极点模型的幅值系数。
步骤4:根据极点值与极点幅值系数调整各个子带互相干。
在步骤1中,Si中的奇异值用于估计两个子带的适当模型阶数。相对较大的奇异值对应于强信号分量,而较小的奇异值通常对应于噪声。对于低噪声水平,在大的和小的奇异值之间有一个急剧的转变,如图2所示。这个转变点可以用来估计模型阶数。但是在较高的噪声水平下,从大奇异值到小奇异值的过渡是非常平滑的,因此在低信噪比环境下精确估计模型阶次会相当困难。

图2 主对角奇异值曲线Fig.2 Main diagonal singular value curve
估计模型的方法有很多,其中比较经典的方法有采用AIC和最终预测误差(final prediction error, FPE )准则等,本文采用一种归一化比值法进行模型估计。设σi(i=1,2,…,m)为矩阵S的奇异值,且有σ1≥σ2≥…≥σm=0,定义归一化比值为
(10)
预先设定一个阈值(如0.990),当p是ρ(k)的值大于或等于该阈值的最小整数的时候,即可认为在矩阵的奇异值中,前p个为主要奇异值,即对应于强的信号成分的奇异值,而后面的奇异值即为次奇异值,对应于噪声奇异值,从而可以将p定为该信号模型的阶数。

(11)
Ai的第一行为dij,表示各个子带的第一行的j个元素,构成如下多项式:
(12)
Ai(z)的根即为各子带的极点值。一般来讲,信号模型的变化会导致极点在复平面上偏离单位圆,但是在每个子带上,这个变化会非常小,所以可以认定主导信号成分的极点更靠近单位圆。于是可以选取最靠近单位圆的Pi个点作为各个子带的极点,得到pi=[p1,p2,…,pPi]。
根据步骤3估计各子带的全极点幅值系数,可以归结为一个线性最小二乘问题,根据式(13)即可得到各子带极点幅值系数。
(13)

随后可以根据式(7)表示各个子带的值Mi(fn),根据步骤4调整各个子带至互相干位置,根据相干函数
(14)
可以得到极点旋转角度Δθ和复振幅稀疏B的最小值。于是,较低子带数据可以由式(15)给出的互相干数据代替:
(15)
这样就完成了各个子带的互相干。在完成各个子带互相干之后,可以进行多子带融合步骤,各子带可以看作根据目标散射点格式由多个正弦波叠加的混合信号,如图3所示。
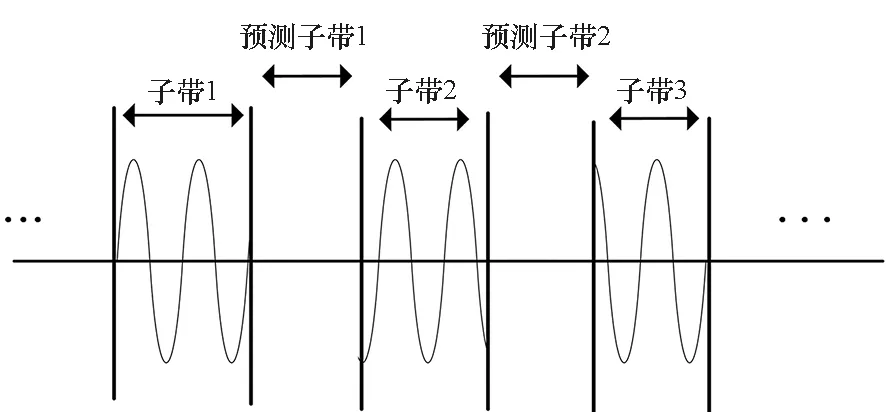
图3 多子带信号示意图Fig.3 Schematic diagram of multi-subband signal
根据Cuomo等[6]提出的全极点模型,提出一种计算更加简便的方式:将多个子带的Hankel矩阵叠加,根据一个Hankel矩阵计算出各个子带需要预测频段的参数,根据将要进行预测的所用子带的Hankel矩阵构建整体前向预测矩阵:
(16)
根据整体前向预测矩阵可以直接求解得到多子带融合信号的极点值和极点幅值,相较于两两子带构造预测矩阵可以减少很大的运算量。按照式(9)进行奇异值分解,得到U、S、V矩阵。然后按照步骤1~3进行计算,得到整体极点值与极点幅值系数。
根据式(7)即可求出预测子带的值,得到全频段信号子带表示如式(17)所示:
(17)
其中,Ni表示各子带频点数,Nmi表示待预测子带频点数。这样就可以得到一个由多子带融合而成的全频段子带。
3 实例仿真
以三段子带信号为例﹐其起始频率分别为f1、f2、f3,频率步进数分别为N1、N2、N3,高低子带的跳频间隔均为Δf,其中f2=f1+ΔB1,f3=f2+ΔB2, ΔB>Δf·N1,ΔB为高子带与低子带起始频率间隔。根据式(1)以两个散射点目标为例,按表1的各子带数据参数进行实验得到各子带信号s1、s2、s3。

表1 各子带数据参数


图4 降噪前主对角奇异值Fig.4 Singular value of main diagonal before noise reduction
当信噪比越低时,奇异值曲线逐渐趋于平滑,对模型精度会有一定影响。对主对角奇异值矩阵按第2节中方法对SNR=-15 dB和SNR=-20 dB的信号进行噪声抑制处理,将噪声分量归置为零或是极小值,对目标主分量乘以权重。得到噪声抑制后的对角奇异值如图5所示。

图5 噪声抑制后的主对角奇异值Fig.5 Singular value of main diagonal after noise suppression
噪声抑制后的SNR=-15 dB与SNR=-20 dB信号主对角奇异值与SNR=10 dB基本重合,且噪声分量低于SNR=-10 dB。根据式(5)重构Hankel矩阵,然后根据式(6)重构信号。对重构后的信号进行傅里叶变换得到距离包络,如图6所示。根据图6可知在距离方向上噪声抑制明显,达到10 dB以上。

(a) SNR=-15 dB噪声抑制后信号距离包络(a) SNR=-15 dB signal distance envelope after noise suppression
为验证算法可靠性,选取SNR=-15 dB进行100次蒙特卡罗实验,并计算均方根误差(root mean square error, RMSE),结果如图7所示。从图7(a)中看出,以信噪比为10 dB的信号脉压值为真值,100次实验均方根误差在0~10 dB范围内浮动,即可认为该算法在噪声抑制方面具有可靠性。为验证在信噪比范围内算法的可行性,选取信噪比范围-20~10 dB,对每个信噪比取值都进行100次蒙特卡罗实验,并以信噪比为10 dB的信号脉压值为真值,计算100次实验的RMSE平均值。由图7(b)可知,各信噪比在噪声抑制处理后相较于10 dB信噪比都有所减小,且与信噪比成反比,即算法在各信噪比情况下都有适用性和可靠性。

(a) 100次实验的均方根误差(a) Root mean square error of 100 experiments

按照第2节中步骤1和步骤2进行计算得到各子带极点值,可以观察噪声抑制前的极点分布,如图8所示。在没有抑制噪声时,低信噪比情况下,极点值不能准确估计。
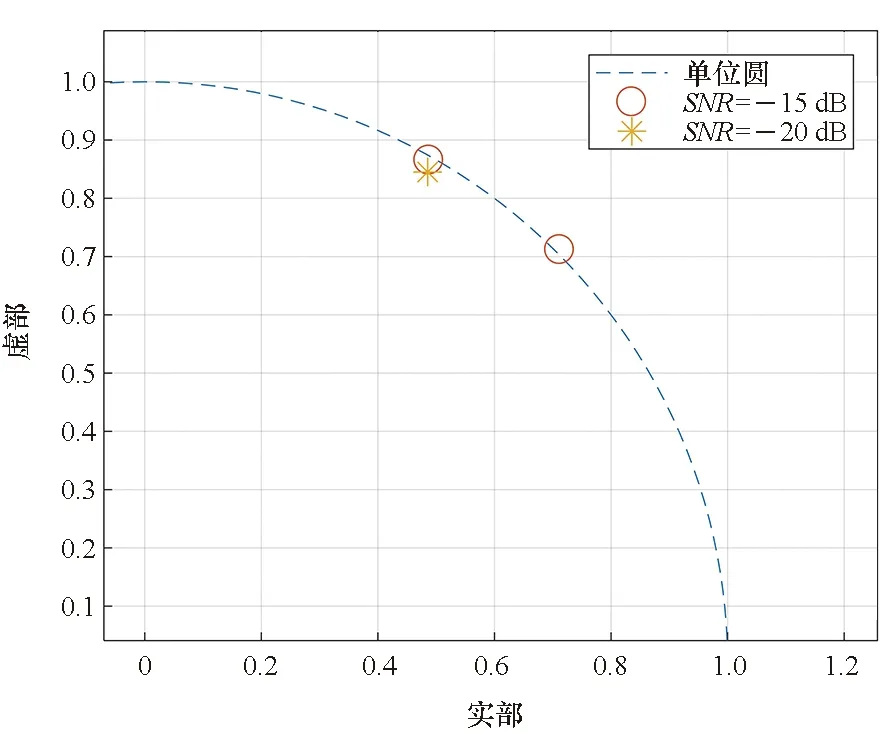
图8 噪声抑制前子带1极点分布Fig.8 Subband 1 pole distribution before noise suppression
各子带未相干前极点分布并不能重合,在单位圆上存在角度偏差,在距离包络也有一定差距,如图9(a)、(c)所示,值与Δθ1与Δθ2一致。完成极点值计算后,按照第2节中步骤3进行极点幅值计算,即可根据式(7)得到子带估计值,根据相干函数即可估计极点旋转角度和复振幅系数值。根据式(15)完成各子带相干,得到相干后的极点分布如图9(b)、(d)所示。对比各子带距离包络,未相干时各子带距离包络无法对齐,相干后各子带距离包络保持一致。

(a) 噪声抑制后各子带极点分布(未相干)(a) Distribution of poles of each sub-band after noise suppression (not coherent)
完成相干后即可对各子带根据式(16)构建整体全极点模型前向预测矩阵,再根据第2节中步骤1、 2、 3进行计算,得到整体极点值与极点幅值系数。然后根据式(7),按照式(17)子带形式进行外推,即可得到全频段信号。若不进行相干处理,两子带外推信号将在频域上不重合,融合信号会在距离包络上产生分量。未相干直接对子带1和子带2进行外推,结果如图10(a)所示;相干后子带1与子带2的外推信号在频域上重合,不会产生多余的距离分量,如图10(b)所示。
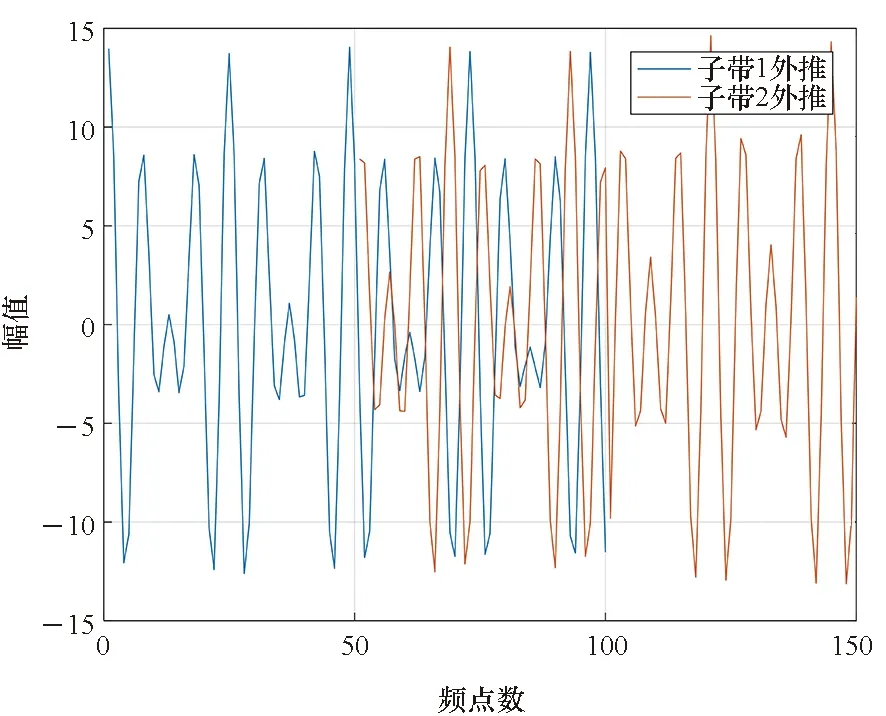
(a) 未相干子带1与子带2外推(a) Extrapolation of uncorrelated subband 1 and subband 2
最终可以获得一个合成宽带信号,当由多个子带融合而成时,信号带宽变大。根据距离分辨单元公式(式中c为光速,B为信号带宽)
(18)
信号带宽与距离分辨单元成反比,带宽越大,能分辨的最小距离单元越小,距离分辨率越高。
多频段融合合成宽带信号如图11所示。由图可知,合成信号与原始信号之间的误差很小,这样拓展带宽后,一些不能分辨的距离也能分辨出。

图11 多频段融合合成宽带信号Fig.11 Multi-band fusion synthesis of broadband signals
通过蒙特卡罗实验,对-30~20 dB范围内信噪比进行100次实验并取无噪声信号为真值计算RMSE的平均值。与不进行噪声抑制直接使用算法进行子带融合相比,进行噪声抑制后,子带模型更加精确,如图12所示。

图12 合成宽带信号蒙特卡罗实验RMSEFig.12 Monte Carlo experiment RMSE for synthesizing broadband signal
4 结论
通过上述实验结果可知,通过在全极点模型中对Hankel矩阵进行奇异值分解这一运算过程中,加入噪声抑制处理,对主对角奇异值进行加权、对噪声分量进行归置,可以大大减弱噪声在全极点模型的模型阶数中对精度的影响,且能更加准确地获得信号检测结果,仿真实验中对信噪比抑制能达到10 dB以上。
在抑制噪声之后,对全极点模型各参数计算更加精确。利用整体全极点模型前向预测矩阵可以将已经相干后的子带直接求得多子带融合信号的极点值与极点幅值系数,减小运算重复量。
