潜艇螺旋桨区域腐蚀电场模型特征及奇异峰成因分析

何 芳,王向军,王晓蓓

(海军工程大学 电气工程学院, 湖北 武汉 430033)

电磁场边值条件一般分为三类:边界电位已知的第一类边值条件(狄利克雷边值条件),如各种金属置于海水中的自腐蚀电位[1-4];电流密度已知的第二类边值条件(诺依曼边值条件),如阴极保护系统中的阳极输出电流[5-8];边界电位和电流密度函数已知的第三类边值(混合边值条件),如阳极、阴极表面的极化曲线函数[9-12]。基于边界元法的潜艇腐蚀电场建模中的边值问题,通常考虑以材料极化状态为边界条件,主要有三种处理方法:一是不考虑极化过电位,采用恒电位边界;二是将极化电位与电流密度视为线性关系,以极化曲线的线性区间作为边界;三是采用材料的非线性极化曲线为边界,引入电极电位或过电位随电流密度变化的函数关系。若边界条件的选取不考虑实际极化状态,所建模型会与实际电场分布产生较大偏差,螺旋桨区域甚至会出现奇异峰现象。

本文采用实测船用921合金钢和镍青铜螺旋桨材料极化曲线作为边界条件,基于边界元法推算潜艇水下腐蚀电场分布,重点对比分析了恒电位和非线性边界条件下的电场特征,并通过建立阻抗谱参数下的船壳-螺旋桨电化学阻抗等效电路,分析了潜艇腐蚀电场螺旋桨区域产生奇异峰的原因。

1 电化学极化参数及阻抗谱测定

电化学试验过程中将船用921合金钢材料、螺旋桨镍青铜材料加工成圆柱状,工作面积为1 cm2,非工作面积用环氧树脂封嵌,实验样片均用金相砂纸打磨,经蒸馏水冲洗,乙醇棉球擦拭,冷风吹干后进行实验。实验温度为20 ℃,介质为 3.5% NaCl 溶液,电化学测试采用CorrTest仪器三电极体系[13],参比电极为饱和甘汞电极,铂丝为辅助电极。测定船用921合金钢材料、镍青铜材料的线性极化曲线,采用动电位扫描法,扫描速度为30 mV/min,线性极化曲线如图1(a)所示,CorrView软件拟合线性极化曲线,腐蚀电流密度和极化电阻参数见表1。测定船用921合金钢材料、螺旋桨镍青铜材料非线性极化曲线,采用动电位扫描法,以20～60 mV/min的电位扫描速度测量,非极化曲线如图1(b)所示, CorrView软件进行最小二乘拟合,计算的腐蚀电流密度及Tafel 斜率参数见表1。921合金钢材料、镍青铜材料的自腐蚀电位测定值见表1。

表1 三种边界条件的电化学参数

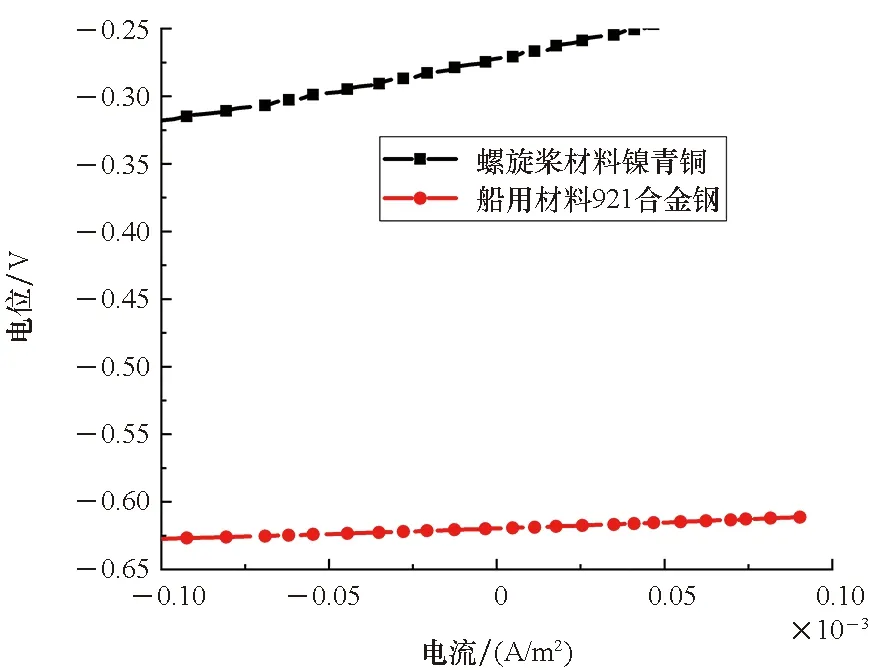
(a) 材料线性极化曲线(a) Linear polarization curve of the material

电化学工作站阻抗测定的频率范围为10-2～104Hz,叠加交流电压幅值为10 mV,船用921合金钢材料、螺旋桨镍青铜材料电化学阻抗测试结果如图2所示。图2电化学阻抗谱图说明电极发生极化时,电极体系所含的不再是理想双电层电容,而是一个常相位角元件[14]。Rs表示船壳与海水接触单位面积的溶液电阻,Rp是船壳极化电阻,R′s表示螺旋桨与海水接触单位面积的溶液电阻,R′p是螺旋桨极化电阻。Q、Q′分别表示船壳、螺旋桨与海水相界面形成的双电层电容,是单位面积的常相位角元件,通常有CPE-T、CPE-P两个参数。CPE-T表示电容值,CPE-P是弥散系数,代表电极表面的电流分布均匀程度,该值越小,电流越不均匀,通常值在 0～1之间,无单位。若CPE-P为0表示纯电阻电路,CPE-P为1表示纯电容电路,CPE-P在0～1之间表示电极表面电流出现了弥散现象,具体的电化学阻抗参数见表2。

表2 电化学阻抗参数

(a) 船用921钢电化学阻抗(a) Electrochemical impedance of marine 921 steel

2 潜艇腐蚀电场模型及螺旋桨区域特征

利用COMSOL多物理耦合场软件仿真,采用二次电流分布场[15]。仿真对象为某型潜艇,长75 m、宽6 m、高7.5 m,按实艇比例建立模型,以平行于潜艇纵向方向由舰艉向舰艏为X轴正方向,以平行于潜艇横向方向由左舷向右舷为Y轴正方向,以垂直于水面指向天空方向为Z轴正方向,笛卡尔坐标系原点位于潜艇几何中心处,潜艇模型螺旋桨为5叶桨,如图3所示。在不考虑潜艇阴极保护电流、不溶性阳极布放位置对电场分布的影响下,设定5叶桨旋转角频率为3.14 rad/s,频率为0.5 Hz。在固定点观测相当于螺旋桨叶1 s时间内变化2.5次,即螺旋桨旋转频率为2.5 Hz。

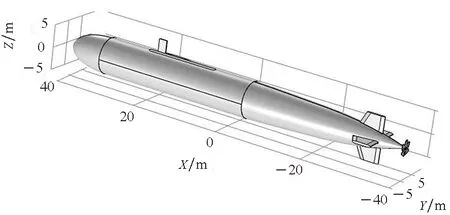
图3 潜艇模型及坐标图Fig.3 Submarine model and coordinate diagram

不同极化条件下的螺旋桨区域电场分布满足拉普拉斯方程,见式(1),恒电位边界见公式(2),式(2)中U为边界面电位分布,φ0为常数。线性极化边界见式(3),式中J为极化电流密度,E0为平衡电位,E为极化电位,Rp为线性极化电阻。非线性极化边界见式(4),式(4)中j0为腐蚀电流密度,ba、bc为阳极、阴极Tafel斜率,不同边界条件下具体电化学参数见表1。

(1)

U=φ0

(2)

(3)

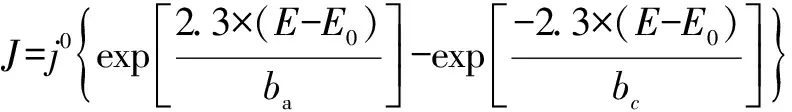
(4)

由于线性边界条件下电位及电场幅值微小,信号特征均不明显,这里主要比较恒电位边界和非线性极化边界下的电场分布。图4为恒电位边界条件和非线性边界条件下的电位等值面对比,恒电位边界电位信号峰瓣规律不明显,故螺旋桨周围电位等值面平滑,如图4(a)所示。非线性边界电位峰瓣明显,三维图上表现为微小的尖峰突起,但非线性边界电位峰峰值相对较小,叠加后这些尖峰突起愈加不明显,每个螺旋桨桨叶周围电位等值面表现为相对平滑,但各个桨叶之间电位等值面不连续,如图4(b)所示。

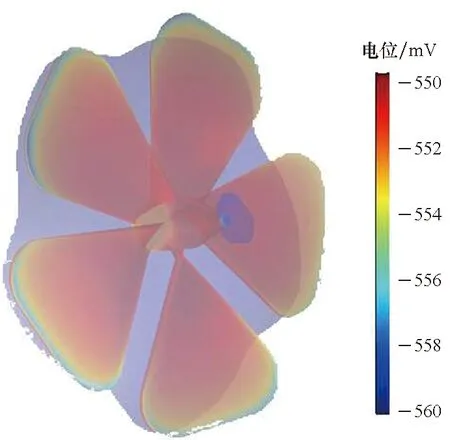
(a) 恒电位边界电位等值面(a) Potential isosurface of the constant potential boundary

恒电位边界条件和非线性边界条件下的电场模值等值面对比如图5所示。恒电位边界条件下的电场模值谐波分量叠加后峰瓣明显,峰峰值远大于非线性边界条件下的电场模峰峰值,其电场模值等值面的三维图像上出现锋利尖角,表现如同异峰突起,故称奇异峰,如图5(a)所示。相对而言,非线性边界条件下的电场模值谐波范围广、谐波分量大,多次谐波叠加后峰瓣显示不明显,其电场模值等值面相对平滑,在三维图像上表现如同水波微动样,不会出现尖角状,如图5(b)所示。恒电位边界与非线性边界下的电场模值时域对比如图6(a)所示,明显恒电位边界条件下电场模值远大于非线性边界条件。二者频域对比如图6(b)所示,仿真螺旋桨旋转频率为2.5 Hz,频域图表现出明显的倍频特征,且为偶次倍频。

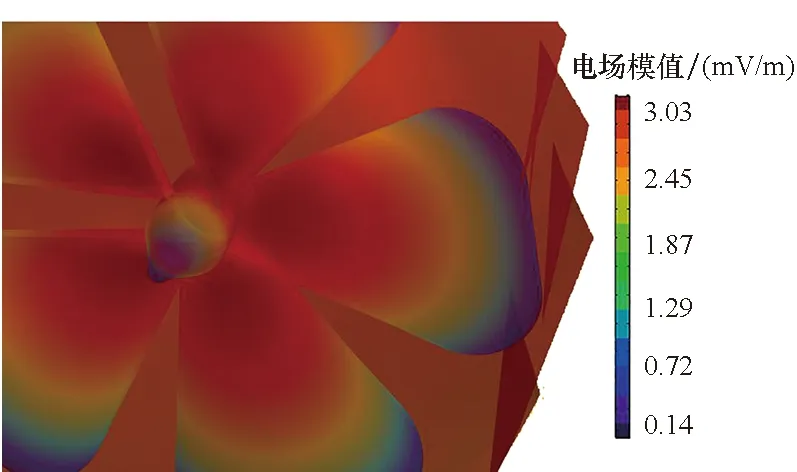
(a) 恒电位边界电场模值等值面(a) Electric field modulus isosurface of constant potential boudary

(a) 电场模值时域图(a) Time domain plot of electric field modulus

3 奇异峰现象的成因分析

潜艇腐蚀电场模型在恒电位边界条件下螺旋桨区域出现了奇异峰现象,非线性边界条件下电场特征均相对平滑,为了探究产生奇异峰的原因,下面结合腐蚀电场产生机理从电化学阻抗等效电路来分析。

潜艇产生腐蚀电场是因为异种金属在海水中会发生腐蚀形成电位差,钢制船壳和青铜制螺旋桨在海水中就像个巨大的腐蚀电池正负极。船体破损处产生腐蚀电流,经过海水流向螺旋桨,再流经船轴回到船壳,形成船壳-海水-螺旋桨-船轴-船壳的闭合回路,建立如图7所示的船壳-螺旋桨的电化学阻抗等效电路,图中溶液电阻Rs和R′s可一起视为海水电阻,其中选用的电化学参数见第1节,等效电路为电阻与电容的混合电路。根据电路原理可知,含有电阻和电容元件的动态电路,由于储能元件的能量积累或释放需要时间,电流改变时电容两端电压不会发生跃变,故电化学阻抗等效电路中的双电层电容电势的变化是连续的、不跃变的。恒电位边界条件是以船壳、螺旋桨材料的自腐蚀电位作为边界,是恒定电位值。此条件下电极系统通过微小外电流时,双电层充电电流小到可以忽略,因此电极电位变化极小,双电层电容可视为用一个电阻为零的导线将其两端短接,电化学阻抗等效电路可简化为纯电阻电路。由电路原理可知,不含动态元件的纯电阻电路中电流改变时,电阻两端电压可以发生突变,故在恒电位边界条件下,电化学阻抗等效电路中的溶液电阻两端电势会发生跃变,电场模型螺旋桨区域会出现奇异峰现象。这里要重点说明的是,在实际海水体系中,电极表面的双电层电容是普遍存在的,不存在纯电阻电路,所以恒电位边界条件的设定可以看作是为了呈现螺旋桨区域奇异峰现象的一个极限条件假设。

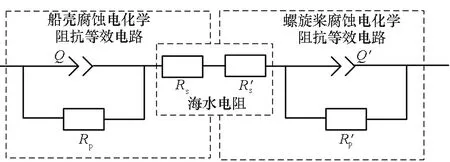
图7 船壳-螺旋桨腐蚀电化学阻抗等效电路Fig.7 Hull-propeller corrosion electrochemical impedance equivalent circuit

为了更清楚地观察螺旋桨区域的电位变化情况,对螺旋桨区域的电化学阻抗等效电路外加恒流源进行仿真,计时10 s后施加1 mA的阶跃电流,对比恒电位边界和非线性极化边界的电化学阻抗等效电路的电位变化。镍青铜材料自腐蚀电位取-320 mV,螺旋桨横截面积半径取r=1 m2,在恒电位边界条件下,溶液电阻参数见表2,溶液电阻π·r2·R′s= 5.78×105Ω·cm2,电化学阻抗两端电位在10 s处直接发生跃变,由-320 mV跃变到-578 mV,如图8所示。在非线性极化边界条件下,电化学阻抗等效电路含有电容元件,镍青铜材料的阻抗谱参数见表2。双电层电容充、放电的快慢通常用时间常数τ来反映,时间常数τ的计算公式为电容值与电阻值的乘积[15]。螺旋桨电化学阻抗等效电路的时间常数为双电层电容值CPE-T′与溶液电阻π·r2·R′s的乘积,即τ=CPE-T′·π·r2·R′s= 38.78 s。工程上一般认为3τ～5τ的时间内完成电容充、放电过程[16],非线性边界条件下的电位变化如图8所示。在图8中,自腐蚀电位由-320 mV开始衰减,在1～40 s时间内电位衰减变化连续,直到200 s时才逐渐稳定至-578 mV。相比于恒电位边界,非线性边界的螺旋桨电化学阻抗两端电压变化不会发生跃变,奇异峰现象会明显减弱。这说明真正能削弱电场奇异峰、减少建模误差的途径在于必须考虑电化学极化,引入固液双电层,螺旋桨区域电势会呈现平滑性改变。

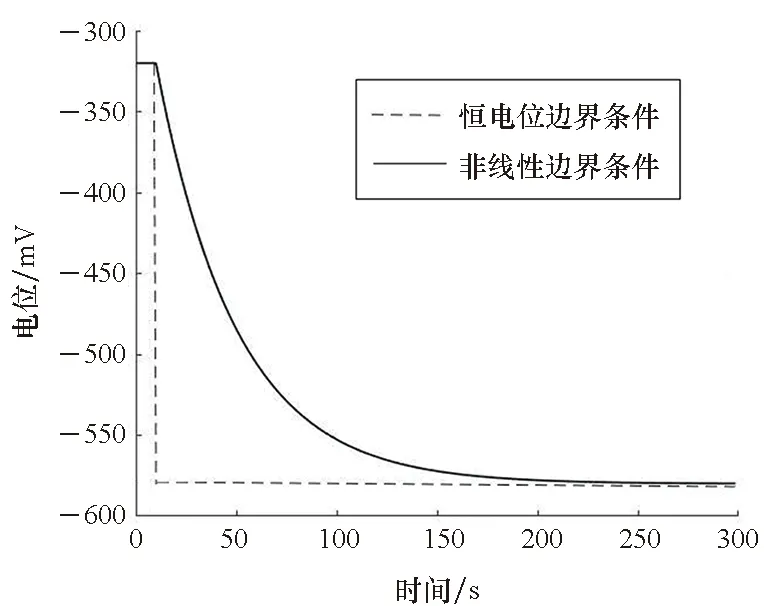
图8 不同边界条件下螺旋桨阻抗两端电位变化Fig.8 Potential change of propeller impedance under different boundary

4 结论

针对边界元法推算潜艇腐蚀电场分布时边界条件影响电场特征的问题,以实测船用921合金钢和镍青铜螺旋桨材料极化曲线作为边界条件,基于边界元法推算潜艇水下腐蚀电场分布,重点对比分析了恒电位和非线性边界条件下的电场特征,并通过建立阻抗谱参数下的船壳-螺旋桨电化学阻抗等效电路,分析了潜艇腐蚀电场螺旋桨区域产生奇异峰的原因。具体结论如下:

1)奇异峰现象与船体材料电化学极化状态有关。采用恒电位作边界条件,螺旋桨区域会出现奇异峰现象,采用非线性边界条件可极大削弱甚至消除奇异峰现象。

2)边界条件选择为恒定电位值,此条件下电极系统通过微小外电流时,双电层充电电流小到可以忽略,电极电位变化极小,可以将双电层电容视为短路,故阻抗两端电势会发生突变。实际海水体系中双电层电容普遍存在,双电层电容视为短路的设定可以看作是为了呈现螺旋桨区域奇异峰现象的一个极限假设。

3)非线性边界条件引入了固液双电层,双电层电容充、放电需要时间,不会跃变,电势变化存在平滑期,非线性极化边界条件的合理参数设定可达到削弱奇异峰现象、平滑腐蚀电场模型的效果。