基于BP神经网络的滚刀载荷解耦方法的研究
2023-06-10杨云兰浩陈莉娜
杨云 兰浩 陈莉娜

关键词:解耦;BP神经网络;有限元分析;标定实验;盘形滚刀
中图分类号:TP391 文献标识码:A
文章编号:1009-3044(2023)12-0100-03
盘形滚刀作为一种挖掘坚硬岩石的刀具,常应用于盾构机和TBM等大型掘进设备。对滚刀载荷进行实时监测,借助不同刀位的滚刀载荷情况从而获得掌子面岩体参数[1],滚刀载荷信息还可作为优化滚刀布置的参考,使刀盘受力更均匀[2]。国内外学者针对上述问题,研发了各具特色的TBM滚刀载荷测量方法,如Samuel等人[3]在掘进机滚刀刀轴上安装应变片,测量到约20min的切削力数据;Zhang等人[4]在正楔齿滚刀和边楔齿滚刀的刀轴上粘贴应变片,实现对滚刀切削力的研究;Entacher等人[5-6]在固定滚刀的螺栓中埋入应变片,运用这些螺栓预紧力在滚刀受力时的数据计算破岩力。应变片安装在刀轴上会影响滚刀的受力性能,而在压块上安装应变片就不存在上述问题,而且有利于保护应变片。将应变片埋入螺栓的测量方法,测量结果只能间接反映三向力的相对大小,并不能直接得到结果。
针对上述问题,设计了一种常压刀盘后装式刀筒载荷实时测量方案,在滚刀压块中间梁位置安装两个贴片传感器,间接获得耦合了垂直力和滚动力的滚刀载荷,结合BP神经网络实现滚刀载荷解耦的过程。
1 滚刀载荷检测传感器布置方案
1.1 滚刀受力分析及应变片粘贴方案
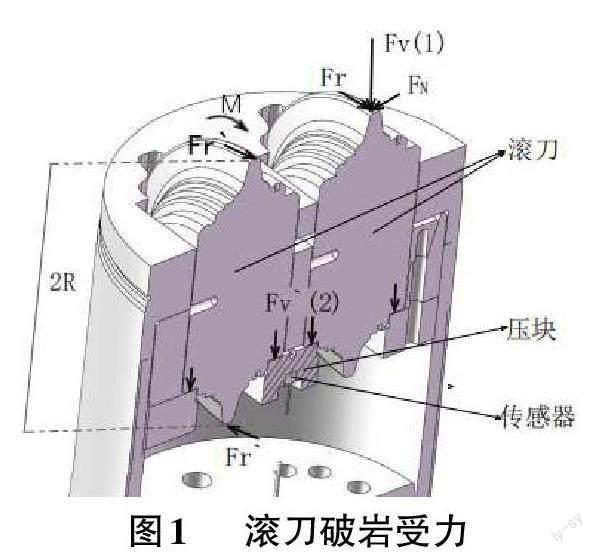
TBM滚刀切削岩石时受到刀盘推力提供的垂直于掌子面的垂直力Fv、刀盘扭矩提供的平行于掘进面的滚动力Fr、边缘滚刀因安装倾角而受到的侧向压力FN。滚刀应力分析装配体剖面如图1,R为滚刀半径,M为弯矩,垂直力和滚动力从刀圈到压块的传导路径为(1)→(2),相较垂直力和滚动力而言,侧向力对正面滚刀影响可忽略不计,因此本文只探討如何解耦得到垂直力和滚动力。
运用workbench19.2,对滚刀载荷下的应力进行数值模拟,采用四面体自动网格划分,总节点数为204938,总单元数为121 687。对滚刀在两种工况下的应力进行仿真计算:工况①为仅受700 kN垂直力;工况②为不仅受700 kN垂直力,还受70 kN滚动力。获得工况①的应力分布如图2所示,在滚刀刀座上选取5 个传感器测点,各测点的应力值如表1所示。由表1 可知,测点A、B、C是主要的受力点,因此最终确定两个传感器的应变片安装位置如图3所示。
1.2 滚刀载荷加载方式及加载范围
受到实验条件限制,目前还没有可以对滚刀加载滚动力的装置,而弯矩可等效于一对力偶,当力矩大小与滚刀直径相等时,力偶可等效于滚动力,因此可通过偏置加载的方式,使滚刀受到弯矩作用,从而实现加载滚动力的目的,弯矩和滚动力有如下关系式:
如图4(a)所示,有中心加载和偏置加载垂直力两种方式,滚刀中心加载时滚刀只受垂直力,偏置加载时受垂直力和滚动力。若偏置加载F1的力,则等效于中心加载大小为F1的力和弯矩M1,如图4(b)所示。贺飞等人[7]已经研究了单刃滚刀的垂直力约为330kN,本文为双刃滚刀,且为了留一定余量,因此设计解耦公式的垂直力范围为0~700 kN,滚动力范围根据垂直力范围、加载方式、滚刀直径等由式(1) 计算得出,为0~140 kN。
2 滚刀仿真实验
由应变片的粘贴位置可知,滚刀同时受到垂直力和滚动力作用时,刀座产生的应变耦合了两种力的效果,若两应变片产生不同的应变,则一定是滚动力作用的效果,因此取两个应变片的应变差值的绝对值来分析其与滚动力的关系,这样才能将滚动力从耦合了垂直力的合力作用中分离出来;垂直力对两个应变片的作用效果一样,因此选取两应变片的应变和值来分析其与垂直力的关系。以滚刀应力分析装配体作为有限元模型,对装配体载荷下的应变进行数值模拟,获得35组应变数据,如图5所示。
图中εh、εc 分别为Ⅰ号标、Ⅱ号标应变片的应变和、应变差的绝对值;M为Fv 大小的0.06倍时、Fv 为M 大小的16.67倍时的应变曲线均是指偏置距离为0.06m情况下加载垂向力的应变数据。
由图5(a)、(b) 可知,当垂直力小于175 kN时,不同工况下应变和、差随垂直力的变化趋势各异,垂直力、弯矩对应变和及应变差均有影响;当垂直力大于175kN时,垂直力仅影响应变和,弯矩仅影响应变差。
3 滚刀载荷试验
通过油压机模拟滚刀施加载荷的标定实验,如图6所示。绘制滚刀载荷试验所得10组数据的应变和、应变差曲线,如图7所示。
由图7可知,圆圈标注位置的大偏差数据会增加电压、载荷之间的非线性,预判该处解耦误差出现最大值;无论弯矩是否存在,电压和都能反映垂直力的大小,且两者基本呈线性相关,电压差只在有弯矩的情况下存在,因此电压差在一定程度上可以反映滚动力。
4 解耦公式及误差分析
4.1 滚刀载荷解耦原理及公式建立
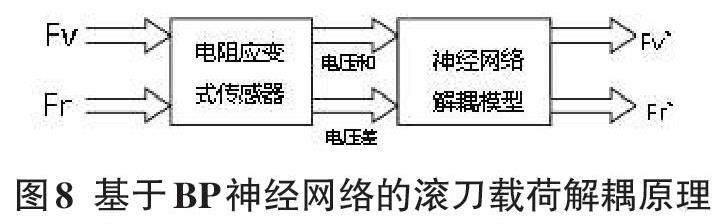
基于BP神经网络的滚刀载荷解耦方法类似于六维力传感器解耦方法,由此可得滚刀载荷解耦原理如图8所示。
理论与实践表明,含有一个隐藏层的BP神经网络具有逼近任何闭区间内一个连续函数的能力[8],因此使用3层神经网络模型进行训练和预测。隐含层节点数选取使得测试误差和训练误差最小的值,通过选取不同的节点数对比分析,最终确定隐藏层节点数为5;网络训练目标为0.001;设置学习率为0.01;最大迭代次数为1 000次;确定函数模型后,选取滚刀仿真实验得到的35个样本作为训练集,建立的垂直力解耦模型的决定系数为0.999 9,弯矩解耦模型的决定系数为0.999 5。选取滚刀载荷试验得到的10个样本作为测试集,对所建模型进行验证,结果如图9所示。
4.2 解耦公式
在实际的工程应用中,贴片传感器输出的是电压数据,因此需要依据电压-应变的转化关系,结合已经建立的应变-载荷解耦模型,实现由电压数据解耦得到垂直力、滚动力,公式如下所示。
4.3 解耦误差分析
测试集所得结果和误差曲线如图9所示。观察图9可知,垂直力单独存在的工况下,在垂直力为175kN 处解耦误差出现最大值,与由滚刀仿真实验及滚刀载荷试验所得预判一致;当垂直力单独作用且小于某值时,误差较大;垂直力、滚动力同时存在的工况下,解耦误差普遍较小。
5 结论
本研究提出的方法为实现滚刀载荷解耦拓展了新思路,克服了因加载条件受限带来的难题。首先进行测点布置方案设计,选定测点后进行滚刀仿真实验和滚刀载荷试验分别获得应变、电压数据,然后以BP 神经网络作为解耦工具获得解耦系数,建立了可直接用于工程实际的电压-载荷解耦公式,标定实验验证电压-载荷解耦公式获得垂直力误差在0.47%之内,滚动力误差在8.85%之内。
