基于自动微分的反应动力学程序设计
2023-06-09苗树伟解德欣刘建鹏叶中豪
苗树伟,解德欣,刘建鹏,叶中豪,郭 峰,*
(1.聊城大学物理科学与信息工程学院,聊城 252000;2.山东省光通信科学与技术重点实验室,聊城 252000)
0 引言
使用计算机模拟,来实现一些实验中不容易监测或一些试验成本过高的状态或过程(例如爆炸和高温燃烧过程,亦或是一些反应非常迅速缺乏测定技术的实验)。科研人员通过对微观世界的原子与分子的动态模拟,来探索新材料的物理特性及其性能,为物理与材料科学的发展奠定基础。目前使用较多的研究方法为分子力学模拟与量子力学计算,量子力学的计算是可以不依靠那些基于实验所得的数据,而直接进行相关的运算并获得物质的几何结构以及电子结构等相关的物质结构,由此也能够获得物质所具有的能量及其物理性质[1]。分子力学则是通过对体系进行相关的数学建模,并对模型中的粒子相互作用抽象化来实现,模型中包含了物理、化学、力学等特性。最后使用分子动力学模拟(molecule dynamics)等一系列计算机运算手段,分析微观体系的运动轨迹以及结构,得出宏观状态下该模型所拥有的物理化学特性。
分子动力学模拟被设定为遵守经典牛顿定律,体系中的所有粒子都在力场中遵循经典牛顿定律进行运动。且体系中的粒子都遵守叠加原理[2−3]。通过计算系统中粒子在多个离散的时刻下的牛顿运动方程就可以得到粒子在这些时刻下的运动信息。
虽然量子力学(QM)方法能够为研究提供很多有用的指导,但也存在部分的缺陷,一旦系统想要考虑整体的运动演化模拟,就需要相当大的硬件系统资源[4]。其他的对于经验原子间势能虽然可以模拟动态的演化,但也需要初始化原子间的连接,对于反应的模拟也存在着一定的缺陷。因此ReaxFF 就被开发,走入人们的视野中[5]。
ReaxFF 是以键级为基础,键级这一概念是由分子轨道理论提出的,能够描述原子间的相互作用以及原子间键的生成与断裂,原子与原子的相互作用不再是只取决于自身的所处位置,而是取决于和该原子相互影响的所有原子[6]。ReaxFF 做到了在保证精度不下降的同时降低了计算的复杂度,更好地加快了计算速度。当我们把ReaxFF 与MD 相结合后,便可应用于更加庞大的模拟体系,并且不需要预设初始的反应状态等条件。ReaxFF反应力场已经在高能材料、有机小分子体系中广泛地使用。ReaxFF 反应力场能够在不多的计算资源下很好地表现出物理与化学的运动及反应过程。
1 模拟方法
1.1 ReaxFF反应力场
ReaxFF反应力场与经验非反作用力场类似,反作用力场将系统能量划分为不同的局部能量贡献[7]。公式为
反应力场的核心是键级Ebond,将原子间的关系建模为一个关于键级的函数,准确描述原子间键所蕴含的能量。函数中包含键能、范德华势能等物理化学能量。Eangle和Eetor为三体价角应变与四体钮角应变所蕴含的相关能量。Eover是一种能量惩罚,它阻止原子的超配位,这是基于原子的价态规则(例如,如果一个碳原子形成超过4 个键,则施加一个严格的能量惩罚)[8]。Ecol和Evdw是计算所有原子之间的静电和色散贡献,而不考虑连通性和键序。反应力场中最小的单位是原子,键级包含了分子内各原子间、各部分的能量。键级的计算函数为
式中:rij为原子间距离;Pbo是经验参数。式中BO'σij、BO'πij、BO'ππij则依次表示单键σ、双键π、三键ππ 的键级,σ、π、ππ 键之间的跃迁不包含不连续。r0为平衡键长。由于键级还未经过矫正,加上各元素的成键也不尽相同,因此会产生很多不合理或者较弱的成键,为了解决这一问题则需要引入修正项。经过一系列的运算,最终得到的总键能公式为
其中:P和De是能量系。
1.2 软件介绍
本研究在ReaxFF已有的基础上对ReaxFF反应力场进行了扩展,编写了一套名为Irff 的代码。Irff 的代码使用了Facebook 人工智能研究院(FAIR)基于Torch推出的PyTorch 库。PyTorch 提供了更灵活的API,可以定义动态计算图,且为张量上的所有操作提供了自动微分(也称为反向传播)[9]。因此我们可以使用Adam 优化器,Adam 算法可以为不同的权重参数分配不同的自适应学习率[10],如此进一步提升了代码的优化能力。并且基于PyTorch的tensor为矩阵的特性,我们对ReaxFF 原有的函数进行了改进,将其改为矩阵运算。经过更改矩阵运算后的公式如下,其中BO'是未经修正的键级。
Etor是表示为二面角势能的键级函数,与键级呈正相关变化,最小值为0。sin Θijk以及sin Θijk均为设置的控制函数在价角180°时保证二面角的能量是0。Etor具有多极值点。
Econj为描述四体作用共轭情况的四体共轭项:
Eval为附加能量,只有当价角处在唯一的最优角度时Eval才为0。Eval与键级呈现正相关的关系,并且是连续的。σ、π 键形成的价角能量各不相同[11]。
2 结果与讨论
我们从LAMMPS程序包中选取了一部分相应的力场文件,并重建一个与其研究过程中建立的模型相近似的模型。使用编写的软件进行计算且将计算结果与通过GULP(general utility lattice pro‑gram)软件计算所得的结果进行比对,以此来证明并保证本软件的计算结果是正确可靠的。
2.1 模型构建
我们参考了文献[12]构建了C2H4 模型,参考了文献[13]构建了C5H8O4N12模型,参考了文献[14]构建了C8H10 模型,以及文献[15]构建了H6CF2 模型。Cell 的晶格向量分别设置为10 × 10 × 10 以及20 × 20 × 20,且具有周期性边界,详情见图1。所有结构建模都采用球棍模型,小球中灰色、红色、蓝色、绿色分别对应的元素为碳、氧、氮、氟。后续小节我们将会采用上述文献中所用的力场文件以及模型来验证我们的程序。
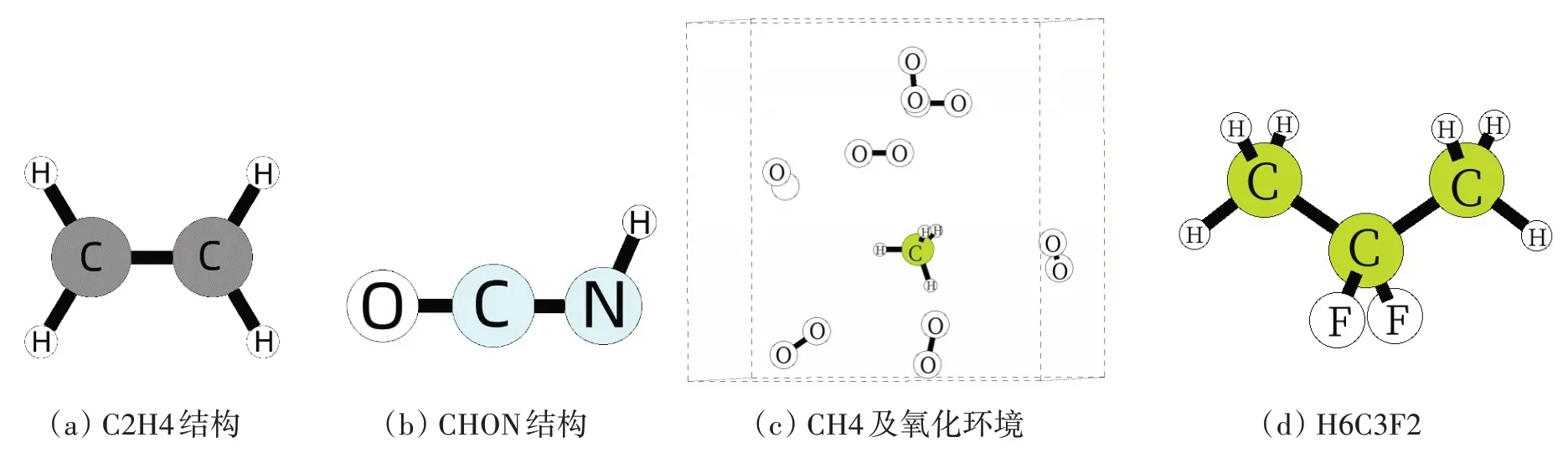
图1 测试本程序设计所用的模型
2.2 MD模拟
分子动力学模拟(MD)是根据所有分子的当前坐标计算分子的受力,根据受力更新分子的坐标,在此过程中收集用于计算宏观性质的有关信息。本文中MD 模拟Time Step 设置为0.1,分子动力学描述的运动是不连续的以时间原子当时所有的各项物理参数。步数设置为100。我们使用了NVE 模拟来生成训练所需的数据,而Velocity Verlet 是实现NVE 集成的唯一动力。步长对于动力学来说是必须的,太小会造成系统资源的浪费,太大会出现“爆炸”。牛顿第二定律的直接积分保留了系统总能量等的参数,因此Velocity Verlet算法是最合适的,在步长大的时候它依然可以使总能量有不俗的稳定表现。需要注意的是NVE模拟中温度一般保持动态的恒定,如果结构产生显著的变化那么温度有可能会发生急剧变化。相较于Runge−Kutta 等的算法,它们确实能在短期能量保存效果上获得不俗的表现,但长时间的模拟则会产生能量缓慢的漂移。
2.3 实验具体细节
在分子动力学模拟中力场(FFs)的精度是核心要素,力场文件中包含了分子内、分子间的势能面(PES)等各种参数。因此我们从LAMMPS中选取了文献[12]中使用的力场参数文件,然后构建乙烯(PE)结构。我们对此PE 结构进行分子动力学模拟并产生一个有一百帧的运动轨迹文件md.traj。然后直接读取该轨迹文件,利用IRFF 函数计算出相应的力场参数。我们分别对比了Ebond键能项、Eover过配位修正项、Eunder配位能校正项、Eang键角弯曲能、Ecoul静电能、Evdw范德华能,以及总能量Total‑Energy。
其中:θ为键角;θ0为平衡键角;kb为键角弯折力常数。二面角扭转能。
其中:Vn为势垒高度;N为多重度;ω为扭转角度;γ为相因子。由于不同的方法计算得出的能量不尽相同,因此只有在同体系的情况下其他构象计算得到的能量才有比较意义。
另外,我们还从LAMMPS 中选取了文献[13‑15]中优化使用的力场文件,进行了与上述相同的操作与计算。得到了四组IRFF 与GULP的参数对比,详见图2~图5。
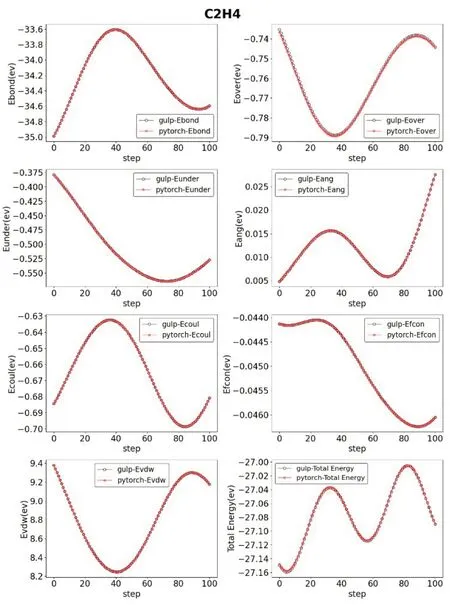
图2 结构为C2H4时相关参数对比
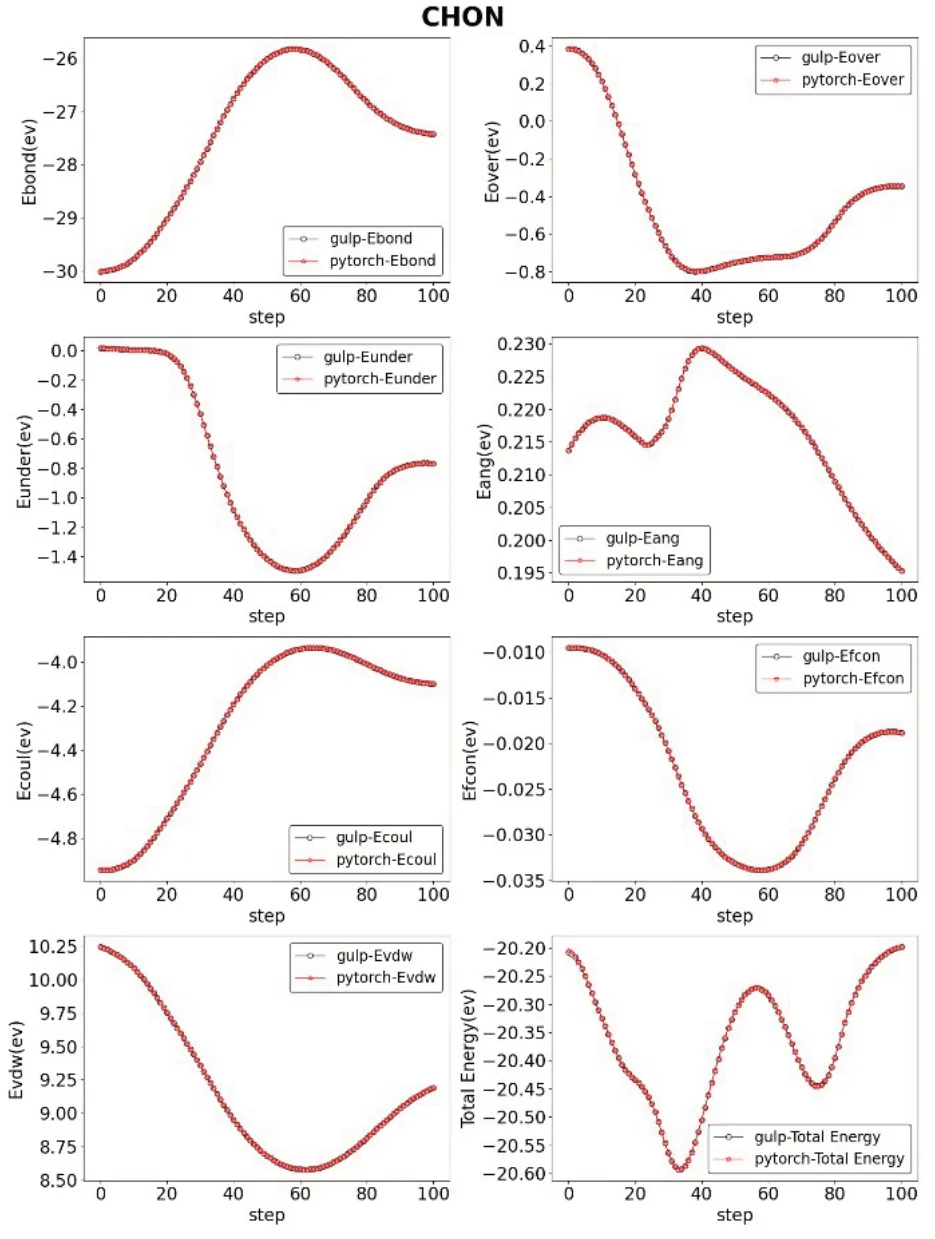
图3 结构为CHON时对比
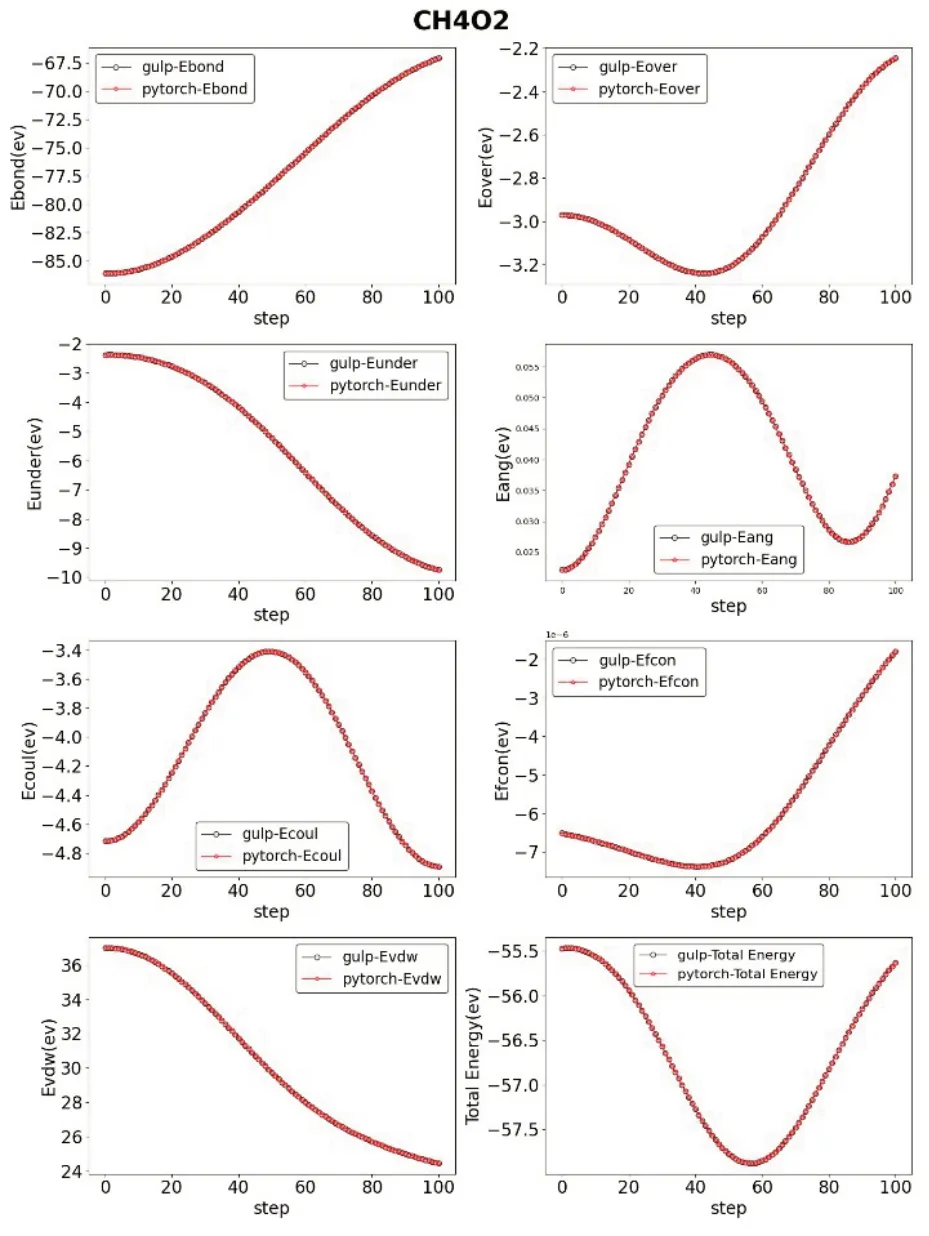
图4 结构为CH4O2时对比
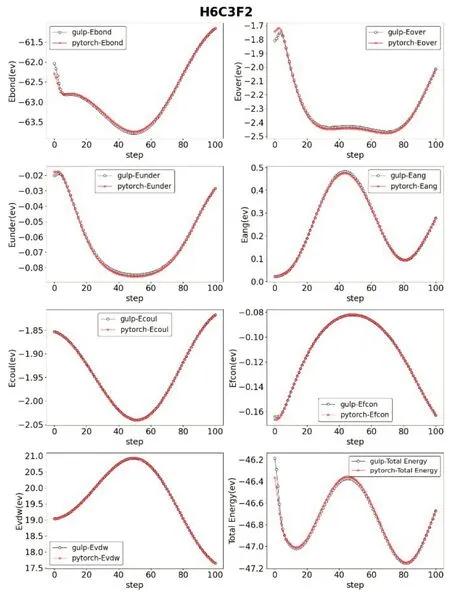
图5 结构为H6C3F2时对比
上述对比可以看出,经过我们矩阵化运算的转换,原子间的各项能量均保持在正常水平范围内。保证准确度不下降的情况下,我们的软件IRFF可以详细地展示出分子运动模拟中各参数的具体数值以及变化情况。将一个反应力场运动模拟的细节直观地展示在了研究人员的面前。
3 结语
本文通过对ReaxFF 反应力场代码的改进构建,改变原有的计算方式为矩阵运算。能够直接使用分子动力学的轨迹文件作为输入数据集,以及引入PyTorch 模块实现了能够自动微分的反应动力学模型。直白地将动力学运动模拟过程中的各种势能函数展现在科研人员的面前,为了解运动模拟过程中的详细情况提供了理论支持。且经过对比验证,证明了改进后的代码的精确性与可靠性。
