锚杆加固公路边坡稳定性

赵念伟

（淄博市交通建设发展中心，山东 淄博 256100）

0 引言

边坡稳定性是公路工程的重要研究内容。边坡加固通常采用抗滑桩、锚杆及格构等方式。其中，由于锚杆加固具有施工简单、造价低等特点，其被广泛应用于公路边坡工程。杨逸飞等[1]基于强度折减法系统地研究了锚杆加固顺层岩质边坡稳定性。周粲铭等[2]基于数值有限元研究了降雨入渗对锚杆加固多级边坡稳定性影响。李忠等[3]基于可靠度理论系统地研究了土体参数变异性对框架锚杆加固黄土边坡稳定性的影响。李帅和林旺照[4]采用极限平衡理论系统地研究了降雨对系统锚杆加固边坡稳定性的影响。结果表明，采用系统锚杆对边坡的加固能力随降雨强度增大而减弱。封永梅和张楠[5]采用理论推导方法研究了高陡边坡锚杆加固的稳定性计算方法。结果表明，边坡的稳定性随锚杆应力增大而增大。加固初始位置越靠近倾覆区，边坡的抗倾覆能力越弱。曹利宏、蒋明镜和周伟等[6-8]基于室内模型试验系统地研究了锚杆加固散粒体边坡的加固机理。结果表明，缩小锚杆直径和增大散粒体直径都可以在一定程度上提升结构强度。

该文基于ABAQUS 数值模拟，系统地研究了锚杆加固边坡效果，研究可为类似工程提供参考。

1 工程概况

某公路博沂线淄博境段长103.924km，起点位于博山区白塔镇，终点位于沂源县与沂水县交界。这次维修段落为沂源鱼台至沂源沂水界段，路线长43.777km，二级公路，路基宽度有16m、15m、13m 三种，相应路面宽度为15m、14m、12m。该路段按建设年限分为三段，鱼台至南石臼段（长8.656km）于2004 年建成，设计车速60km/h，2011 年对行车道按8m 宽范围实施中修罩面，罩面厚度3cm，两侧硬路肩设1m 宽渐变段；南石臼至石桥段（长13.658km）于2007 年大修，设计车速60km/h；石桥至沂水界段（长21.459km）于2002 年改建，设计车速40km/h，2010 年实施全幅中修罩面，罩面厚度3cm。其中2006 年青兰高速建设中有对3 个路段进行改线，长2.391km。这次对鱼台至南石臼段（K60+147～K68+802，长8.656km）及石桥至沂水界段（K82+460～K103+924，长21.459km）实施大修；南石臼至石桥段（K68+802～K82+460，长13.658km）实施中修罩面。

设计标准：维持原有公路等级标准，鱼台至石桥段设计车速采用60 km/h，石桥至沂水界段设计车速采用40km/h；改造的桥涵采用公路-I 级荷载标准，利用桥涵维持原荷载标准。

道路路基采用分层碾压方式进行处理。回填压实度大于96%以上。路基边坡坡率为1 ∶1.5。沿线路段典型路段边坡经计算边坡稳定性为1.23。根据规范安全性要求，规定路基边坡的稳定性系数不得小于1.25。因此有必要对边坡进行治理。该项目拟采用锚杆对该路基边坡进行加固，锚杆共布置5 排。对采用锚杆加固后的边坡进行稳定性分析。

2 数值模型

2.1 有限元模型建立与网格划分

基于实际路基边坡建立计算模型。边坡模型断面宽度取为33 m，边坡的最大高度为16m。根据钻孔取样及室内土工试验，该文对模型中所采用的土体的物理力学参数见表1。岩土体计算本构采用摩尔-库伦，锚杆选择cable 单元进行模拟，计算本构为线弹性。模型的边界条件为底部约束3 个方向的自由度。左右两侧施加水平方向的约束，顶部为自由面。网格划分总数为10 000 个，节点数为7800 个。图2 为边坡锚杆布置方式，锚杆共布置5 排。

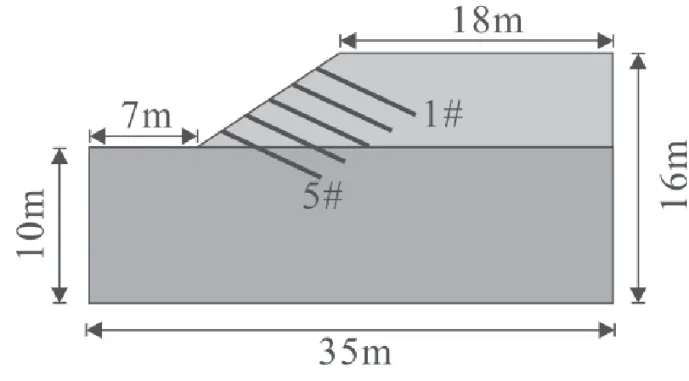
图2 边坡锚杆布置方式

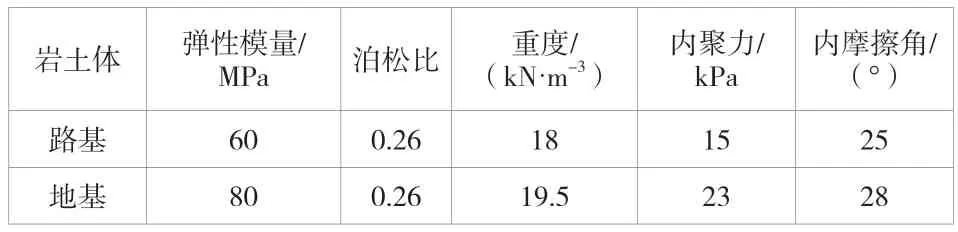
表1 材料力学参数

2.2 计算参数

经现场取样，在实验室试验，得到岩土体材料力学参数见表1。

表2 为该文采用锚杆的参数。

表2 锚杆参数

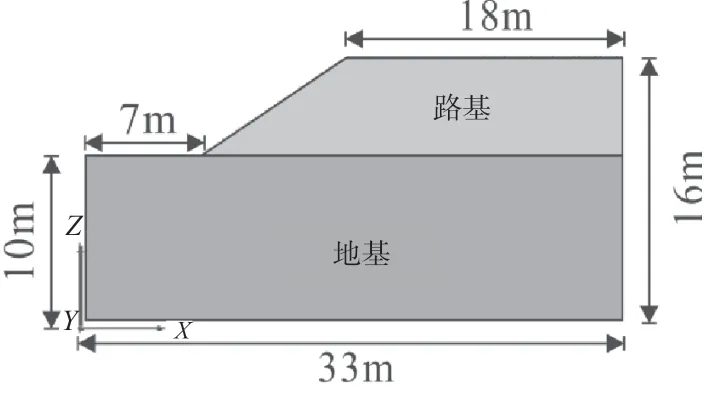
图1 边坡典型剖面图

3 计算结果与分析

3.1 加固前后边坡稳定性

天然工况下，边坡的稳定性达不到规范要求。该项目采用锚杆对该路基边坡进行加固。进一步对采用锚杆加固后的边坡进行稳定性分析。结果表明，采用锚杆加固后边坡的稳定系数提高至2.2，以未采用锚杆加固的稳定性提高了80%。当锚固穿过滑面时，可以显著提高抗滑作用力，提高土体的抗剪强度，阻止滑体发生破坏。此外，锚杆可以与周围土体形成复合加筋土，也可以有效地提高边坡的稳定性。

3.2 锚杆长度和倾角对边坡稳定性的影响

为研究锚杆长度和锚杆倾角对边坡稳定性的影响，该文计算了不同锚杆长度和不同锚杆倾角工况下边坡的稳定性，如图3 和图4 所示。图3 结果表明，边坡的稳定性系数随锚杆倾角的增大而先增大后变小。在锚杆长度分别5 m、6 m、7 m 和8 m，当锚杆倾角为0°时，边坡的稳定性系数分别为1.31、1.32、1.42 和1.57；当锚杆长度分别5 m、6 m、7 m 和8 m，当锚杆倾角为60°时，边坡的稳定性系数分别为1.61、1.54、1.50 和1.42。总体来看，当锚杆倾角为25°时，边坡的稳定性系数达到最大。因此，在实际工程中，可将锚杆倾角20°～30°作为锚杆的最优下倾角。

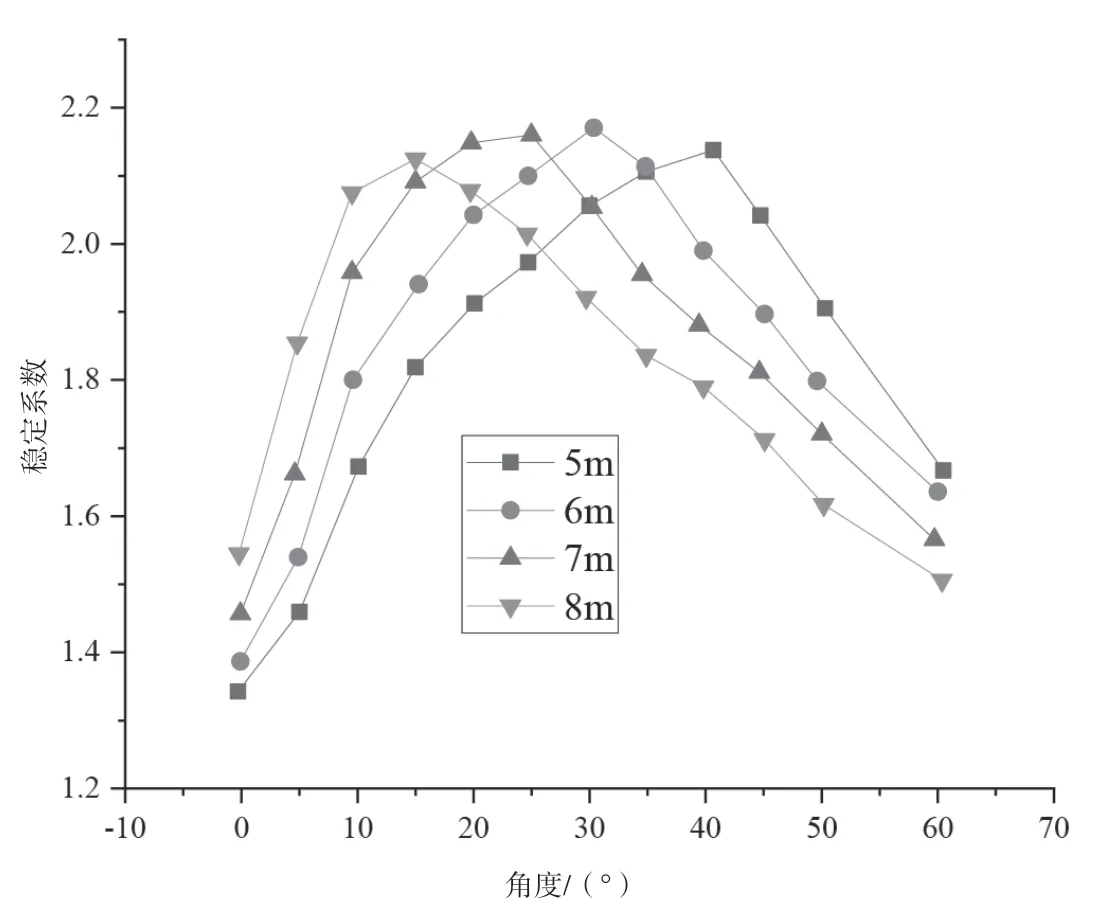
图3 锚杆倾角对边坡稳定性

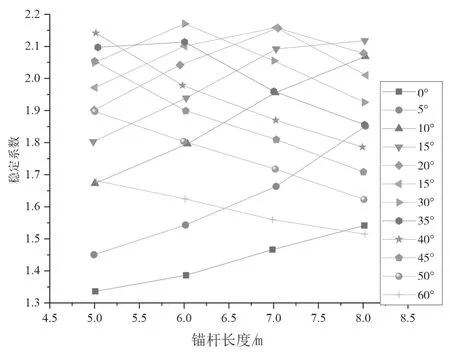
图4 锚杆长度对边坡稳定性

图5 锚杆间距对边坡稳定性的影响

图4 结果表明，当锚杆长度为5 m，锚杆倾角为0°时，对应的边坡稳定性系数最大值为1.35。边坡的稳定性随锚杆的长度增大而增大。此外，根据图6 结果可知，不同的锚杆长度所对应的最优锚固角有所不同。以该文研究对象为例，当锚杆长度为5 m 时，对应的最佳倾角为40°，当锚杆长度为6m 时，对应的最佳倾角为30°，锚杆长度为7m 时，对应的最佳倾角为25°，当锚杆长度为8m 时，对应的最佳倾角为15°。

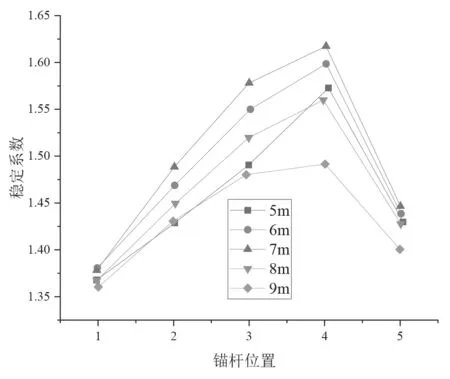
图6 锚杆位置对边坡稳定性的影响

3.3 锚杆间距对边坡稳定性的影响

进一步研究不同组合中锚杆长度和锚杆倾角基锚杆间距对边坡稳定性的影响。图5 为当锚杆间距不同时，锚杆长度与边坡稳定性的关系以及不同锚杆长度下锚杆间距与边坡稳定性的关系。图5（a）结果表明，在固定锚杆间距不变的情况下，边坡的稳定性随锚杆的长度增大而先增大后变小。当锚杆长度不变时，不同的锚杆间距对应的边坡稳定系数最大值有所不同。以锚杆长度为7 m 为例，当锚杆间距为0.92 m 时，边坡为稳定系数为2.24；当锚杆间距为1.54 m 时，边坡的稳定系数为2.15；当锚杆间距为1.85 m时，边坡为稳定系数为2.08；当锚杆间距为2.3 m 时，边坡为稳定系数为1.95；当锚杆间距为3.1 m 时，边坡的稳定系数为1.76。

根据图5（b）的结果，当锚杆长度小于7 m 时，边坡的稳定性随锚杆间距增大而呈线性增大，当锚杆长度大于7 m时，边坡的稳定系数随锚杆间距增大而呈曲线增大。

为研究锚杆位置变化对边坡稳定性的影响，该文分别在图3 中分别改变锚杆位置进行研究。假设在边坡的5 个位置设置单排锚杆，第一次计算假定只有一排锚杆，第二次计算有2 排锚杆，并以此类推。计算得到锚杆位置对边坡稳定性的影响结果如图6 所示。结果表明，在其他条件不变的情况下，当锚杆位置由坡顶向下移动时，边坡稳定性先增大后变小，当锚杆位置在4#位置时，边坡的稳定性最大，稳定性系数分别为1.55、1.57、1.60、1.55 和1.46。综合来看，对于单排锚杆，边坡的稳定性随锚杆长度的增大而增大，而增大且当锚杆长度等于7 m 时，边坡趋于稳定，锚杆对边坡稳定性加固效果变弱。此外，根据分析，在该文研究的范围内，当锚杆长度为7 m 且锚杆布置在坡脚中下部时，边坡加固方案最优。

4 结论

该文采用有限元方法研究了锚杆加固某路基边坡的效应，并对锚杆参数进行计算，分析了锚杆对边坡稳定性的影响，得到以下3 个结论：1）采用锚杆加固路基边坡可以使边坡的稳定性显著提高80%。当锚杆长度不变时，边坡的稳定性随锚杆倾角的增大而先增大后变小且不同长度的锚杆对应的锚固角有所不同。2）当锚杆间距不变时，边坡稳定系数随长度增大先增大后变小，当锚杆长度等于7m 时，对应的边坡稳定系数为临界长度。3）锚杆布置在坡体中下部时对提高边坡的稳定性最优。